基于卷积神经网络的水下湍流探测技术

贺锋涛，吴倩倩，张建磊，杨祎，张娟，姚欣钰，赵伟琳

（西安邮电大学 电子工程学院，西安 710072）

0 引言

水下航行器在水下环境中具有广泛的应用潜力，涵盖海洋资源勘探、海底地质调查以及水下作业等多个领域。然而，水下湍流对于水下航行器的航行构成了严重挑战，直接影响其环境感知和定位能力，从而削弱了其任务执行能力和性能表现［1］。因此，精准地探测水下湍流对于水下航行器的航行决策和性能提升至关重要。通过精确地感知湍流并根据其信息做出相应调整，水下航行器可以增强在湍流环境下的航行稳定性和能力，更好地适应复杂的水下工作任务和环境需求。尽管目前声学方法是探测水下湍流的主要途径［2，3］，但在复杂环境下仍存在一定的限制。与此不同，散斑图像是由激光与粗糙表面或空气中微小不均匀性相互作用所形成的明暗相间图案。考虑到物体的表面形态和内部结构的多样性，散斑图像的形态和分布会受到多种因素的影响。透过对散斑图像的深入分析，我们可以获得物体的表面形态、纹理特征、表面缺陷以及内部结构等丰富信息［4］。因此，由于散斑图像所蕴含的丰富信息，这种方法在科技领域得到广泛应用，为各领域带来新的研究和应用前景。

在水下环境中，光能量受到水分子的吸收和散射影响，导致信号强度逐渐减弱，传输距离也受到限制［5］。湍流的存在对散斑图像产生多方面影响，包括散斑强度的变化和波前相位的扰动等，这使得散斑图像的预测和分析变得复杂且困难［6］。尽管有许多学者利用干涉理论对水下湍流进行了测量研究，但在基于散斑图像的水下湍流探测方面的研究相对较少。王翰韬及其团队运用高斯-谢尔模涡旋光束进行了水下湍流探测的研究。他们首先采用了传统的平面波马赫-曾德尔干涉仪方法，系统地研究了光束在不同湍流场中的传输特性以及双光束干涉的特性。此外，他们还在非均匀湍流场下探讨了该方法的测量应用［7］。另一方面，张家瑞等研究团队通过分析涡旋光束与高斯光束在湍流场中干涉产生的条纹偏移特征，开展了关于水下湍流强度的探测研究［8］。石鹏宇等通过旋转刚体模型的仿真研究，探索了应用涡旋光的旋转多普勒效应来探测流体局部涡量和速度［9］。

本文提出了一种基于水下湍流影响的散斑图像测量温差耗散率XT的方法。基于功率谱反演法和惠更斯-菲涅尔原理仿真得到水下湍流影响下的散斑图像数据集，并利用卷积神经网络处理散斑图像，实现从图像到XT数值的测量，最后通过现场实验验证了该方法的可行性，为散斑图像在水下流场探测中的应用提供了理论和实验基础。

1 水下湍流对激光束传输的影响

1.1 水下湍流模拟

Nikishov 模型指出水下湍流中折射率的波动可表示为温度和盐度波动的共同作用，并使用指数型函数来描述折射率的空间功率谱［10］。然而，Nikishov 模型没有考虑到海洋湍流外尺度对光学特性的影响。为了解决这个问题，将现有的大气湍流外尺度模型应用于Nikishov 的海洋湍流折射率功率谱，从而得到三种外尺度模型下修正后的Nikishov 湍流折射率功率谱［11］，即

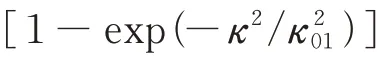
在短距离传输和弱湍流区域中，湍流对光束的影响可以简化为纯相位扰动。为了研究湍流对光波的影响，可以使用符合湍流理论统计特性的随机相位屏来模拟湍流效应。利用指数型Nikishov 谱修正的谱模型，并采用蒙特卡洛方法，通过功率谱反演法，可以获取相邻相位屏之间湍流引起的相位扰动的统计信息［12］，即

式中，ϕθ(κx，κy)=2πk2×Δz×ϕn(κx，κy)，ϕθ(κx，κy)为水下湍流在垂直于传播方向上的湍流相位功率谱，ϕn(κx，κy)为修正后的指数型Nikishov 谱。

1.2 湍流影响下的散斑图像

当激光光束穿过湍流介质时，湍流场引起的介质折射率随机起伏会对光束传输特性产生显著影响。出射光场的复振幅［13］可表示为

式中，(x0，y0)表示出射光所在平面上的直角坐标，实数标量场A0(x0，y0)和ϕ0(x0，y0)分别表示振幅与相位，假设不同空间位置的A0和ϕ0是随机数，且两者无关。基于惠更斯-菲涅尔原理，出射光场在传输至接收端处的z平面时，其复振幅将受到传输路径上各点的相位差和振幅衰减的影响，表示为

通过公式可以仿真得到水下湍流影响下的散斑图像如图1所示，具体仿真参数如表1所示。

图1 标准散斑图像及不同强度水下湍流影响下的散斑图像Fig.1 Standard speckle images and speckle images under the influence of underwater turbulence of different intensities

表1 仿真参数Table 1 Simulation parameters

图1（a）展示了一个未受湍流影响的典型散斑图像，散斑颗粒明显。图1（b）～图1（g）展示了在不同温差耗散率下受到湍流影响的散斑图像。从这些图像中可以观察到，湍流的存在导致散斑颗粒的模糊化，并引起了不同程度的畸变，特别是随着湍流强度的不断增大，当温差耗散率达到一定量级时，散斑畸变程度最大。

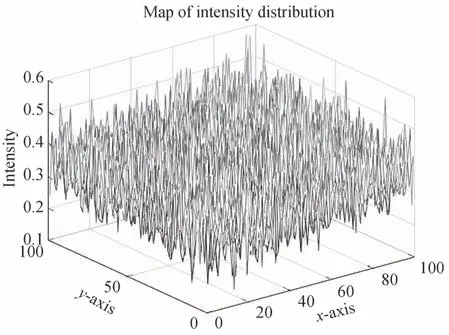
图2 光强分布Fig.2 Light intensity distribution

2 基于卷积神经网络的温差耗散率的测量

2.1 总体框架

本文提出了一种名为深度可分离ResNet-50 与Transformer 网络（Deep Separable ResNet-50 with Transformer Network，DRTN）的水下湍流测量方法。该方法包括深度可分离ResNet-50 和Vision Transformer（ViT）两种网络结构，如图3所示。为了提高分类器的准确性和鲁棒性，对水下湍流的散斑图像进行预处理。预处理过程包括提取频谱信息、梯度信息和纹理信息，并将它们叠加在一起生成多特征融合图像。这样做可以提供更全面和丰富的图像信息，有助于更准确地进行湍流测量。在DRTN 中，深度可分离ResNet-50 模型被应用于处理多特征融合图像。深度可分离ResNet-50 模型使用深度可分离卷积替换了ResNet 中的3×3 卷积操作。此外，通过引入跳跃连接来解决梯度消失问题，从而提高了模型的训练稳定性和速度，并提升了模型的精度和泛化性能。另一方面，DRTN 中的Vision Transformer 部分利用自注意力机制处理图像中的局部特征。它将图像分成固定大小的小块，并使用Transformer 模型处理这些小块的特征表示。这种方式能够有效地捕捉图像中的局部和全局信息，有助于更好地理解和测量水下湍流。通过将深度可分离卷积和Transformer 机制应用于水下湍流测量中，DRTN 能够充分利用多特征融合图像的信息，并通过跳跃连接和自注意力机制提高模型的稳定性、精度和泛化性能。

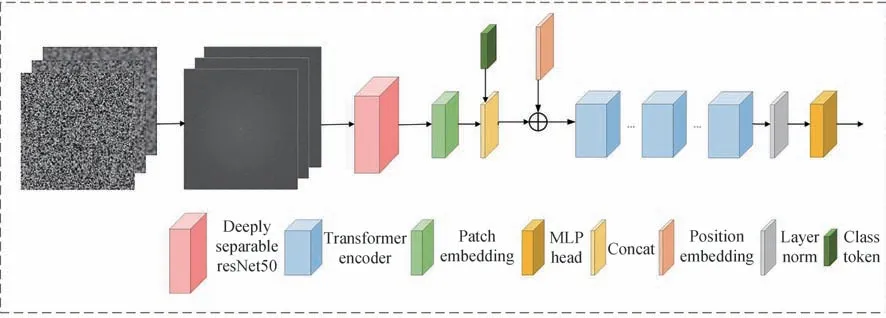
图3 总体架构Fig.3 Overall architecture

2.2 数据预处理

为了增加分类器的准确性和鲁棒性，使用多特征融合图像进行特征提取，如图4所示。其中，频谱图像反映了图像中的频率分量情况，如图4（a）所示，梯度图像、纹理图像反映了图像中的边缘信息和纹理信息，如图4（b）、（c）所示。将它们叠加在一起得到多特征融合图像，如图4（d）所示，其提供了更全面和丰富的图像信息，增加了分类器的准确性和鲁棒性。

图4 多特征融合图像Fig.4 Feature image

2.3 深度可分离ResNet 模型

ResNet 网络［15］是在2016年由微软实验室提出，斩获当年ImageNet 竞赛中分类任务第一名，目标检测第一名。该网络模型提出残差结构，并搭建超深的网络结构，在该残差结构当中，主分支使用了三个卷积层，第一个是1×1 的卷积层用来压缩channel 维度，第二个是3×3 的卷积层，第三个是1×1 的卷积层用来还原channel 维度。但是在传统的3×3 卷积中，所有通道的特征都是在同一步骤中提取的，这可能会导致信息的混淆和冗余。为了解决这个问题，本文提出的R50 的卷积层采用的是stdConv2d，并将标准的3×3 卷积替换为深度可分离卷积，然后将所有的BatchNorm 层替换为GroupNorm 层，如图5（a）所示。在原ResNet50 网络中，stage1 重复堆叠3 次，stage2 重复堆叠4 次，stage3 重复堆叠6 次，stage4 重复堆叠3 次，但在这里的R50 中，把stage4 中的3 个Block 移至stage3 中，所以stage3 共重复堆叠9 次。并在每个残差块的第一个卷积层和第二个卷积层之间增加了一个深度可分离卷积层，每个深度可分离卷积层包括深度卷积和逐点卷积两个步骤［16，17］，如图5（b）所示。深度卷积先对每个通道进行卷积，从而分离出通道之间的信息。接下来，逐点卷积使用1×1 的卷积核将所有通道的特征进行组合，生成新的特征表示。采用stdConv2d 和GroupNorm 的改进使得模型对批量大小的依赖减少，适应小批量数据，降低计算代价，并提高了模型的泛化能力，其次，深度可分离卷积在计算复杂度和参数量方面都有更好的表现。

图5 深度可分离ResNet 模型Fig.5 Deep separable ResNet model

2.4 Vision Transformer

ViT［18］是一种基于Transformer 架构的视觉感知模型，最初是为了解决图像分类任务而提出的。与传统的卷积神经网络不同，ViT 利用自注意力机制来建模图像中的全局上下文关系，从而实现对图像的全局感知。其核心思想是将输入的图像分割成一系列的图像补丁，然后将这些补丁通过一个线性变换映射为向量序列，作为Transformer 的输入。然后通过多层的Transformer 编码器，如图6（a）所示，ViT 能够对这些向量进行逐层的特征提取和表示学习，以获取图像中的语义信息，而多层感知器是由两个线性层和一个激活函数（如ReLU）组成，如图6（b）所示，其中第一个线性层将输入的向量映射到一个中间向量，第二个线性层将该中间向量映射回原始的向量空间。

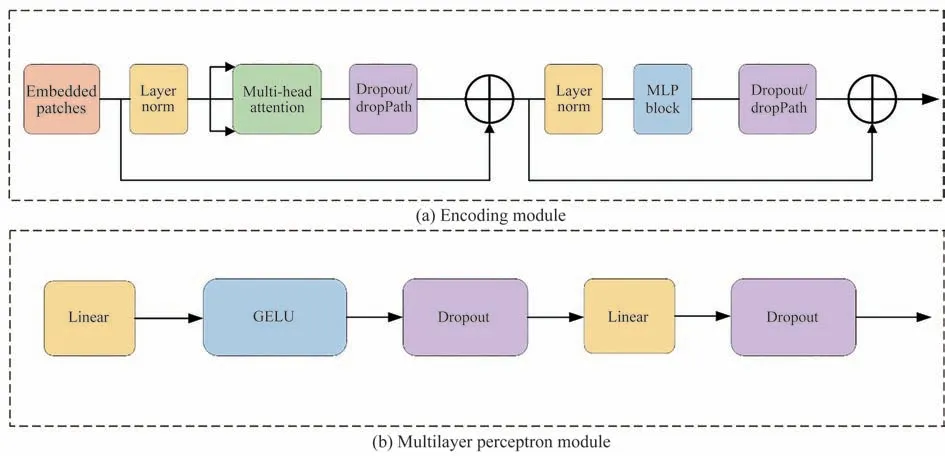
图6 Transformer 机制Fig.6 Transformer mechanism

2.5 模型评价

本文随机选取10-4～10-8范围内的XT，并得到与之相对应湍流影响下的散斑图像。为了训练网络模型并评估其训练效果，按照9∶1的比例划分了一共2 500张图像。其中，选择2 250张图像作为训练集，用于模型的训练过程。同时，保留250张图像作为测试集，用于评估训练后模型的性能表现。利用搭建好的深度学习模型，将处理后的散斑图像数据集输入神经网络模型中进行训练，训练过程中的分类精度曲线和损失值曲线分别如图7所示。可以看出，随着迭代次数的增加，分类精度曲线和损失值曲线逐渐达到收敛，且收敛效果较好。

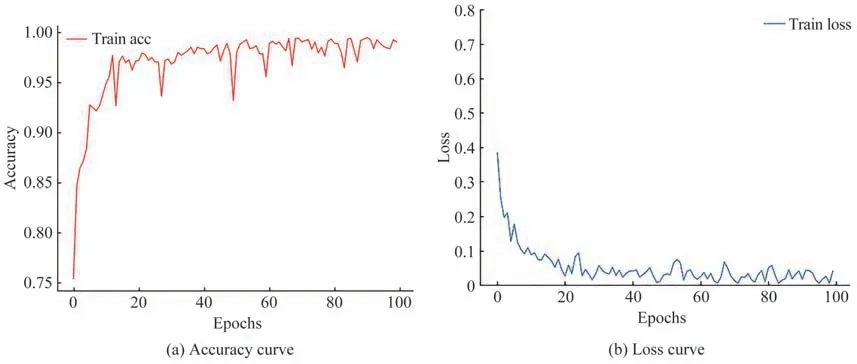
图7 模拟数据集在该模型上的分类精度曲线和损失值曲线Fig.7 The classification accuracy curve and loss value curve of the simulated dataset on this model

2.6 模型对比

为了评估识别结果的可靠性，实验中使用了准确率、精确率和召回率作为评价指标。在机器学习领域，准确率（Accuracy，A）是一种常用的性能指标，用于衡量分类器在正确分类样本与总样本数之间的比例。精确率（Precision，P）和召回率（Recall，R）是用来评估分类器在预测正类时的准确性和覆盖率的重要指标。其计算公式表示为［19］

式中，Tp表示正确预测为该等级的样本数，Fp表示错误预测为该等级的样本数，Tn表示正确预测为其他等级的样本数，Fn表示错误预测为其他等级的样本数。

不同分类网络在XT测量上的性能指标的实验结果见表2 和图8。

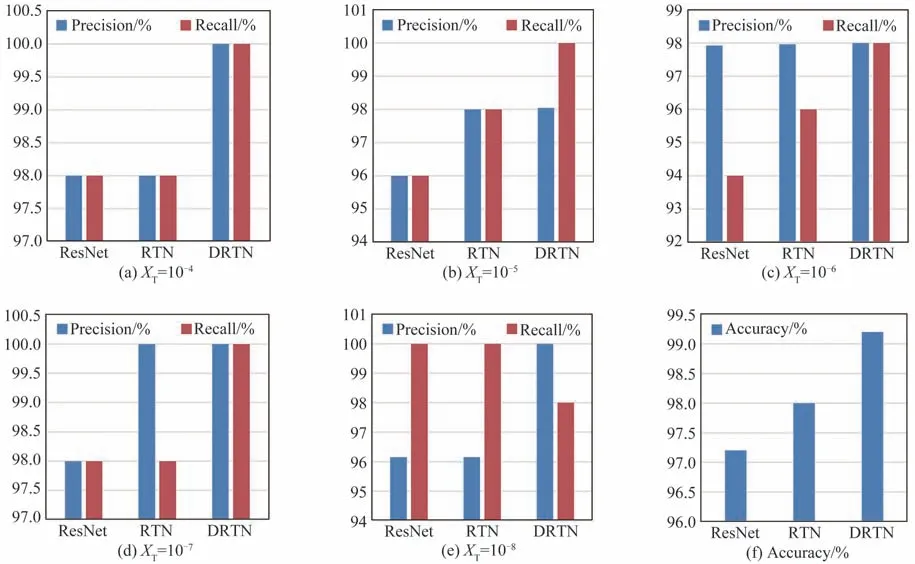
图8 不同分类方法在准确率、精确率和召回率方面的表现Fig.8 The performance of different classification methods in terms of accuracy，precision，and recall

表2 不同分类网络在模拟数据集XT 测量上的性能指标Table 2 XT performance indicators of different classification networks in simulated datasets

该模型在准确率方面表现出色，达到了99.2%，相比ResNet 和ResNet-50 与Transformer 相结合的网络（ResNet-50 with Transformer Network，RTN）分别提高了2.0%和1.2%。此外，本文模型在平均精确率和召回率方面也取得了显著提升，相比ResNet 和RTN 分别提高了1.994%和1.186%，以及2.0%和1.2%。这些结果表明该神经网络模型在准确测量温差耗散率方面具有优异的性能。

3 实验验证

本实验旨在测量不同温差耗散率下520 nm 蓝绿激光束在水下湍流环境中传输一定距离后的散斑特性。如图9所示，从激光器中输出的激光通过光纤1 传输至水下环境中，经过湍流影响后由光纤2 传输至显微装置，采用光纤固定卡将两根光纤对准，确保光纤1 和光纤2 之间激光束的稳定传输，以获取携带水下环境信息的湍流信号，520 nm 蓝绿激光束在水中的折射率为1.333，此时激光束从光纤1 垂直入射到光纤2 的距离为1 cm，经过计算光程为1.333 cm，若激光束从光纤1 倾斜出射至光纤2 倾斜入射，两根光纤的距离则大于1 cm，此时光程则大于1.333 cm。本文使用的显微镜为佳康捷金相显微镜，型号为JKJ-403D，具备高分辨率特性，如图10所示。光束通过光纤2 传输到聚光镜上，然后经过孔径光阑会聚，并由聚光棱镜进一步集聚。接着，通过分束器将光束分为两个方向，其中，一个方向的光束经过辅助物镜转换为平行光，照射在平面反射镜上。经过平面反射镜反射后，分光镜改变光路，最终通过棱镜形成放大倒立的实像，然后通过目镜接收出射的光束，该光束经过CCD 摄像头拍照采集后传输至计算机进行存储，上位机采用IC capture 2.1 软件采集数据集。最后利用Python 语言对采集的图像数据进行处理与分析，以测量水下湍流信息。

图9 实验装置Fig.9 Experimental device

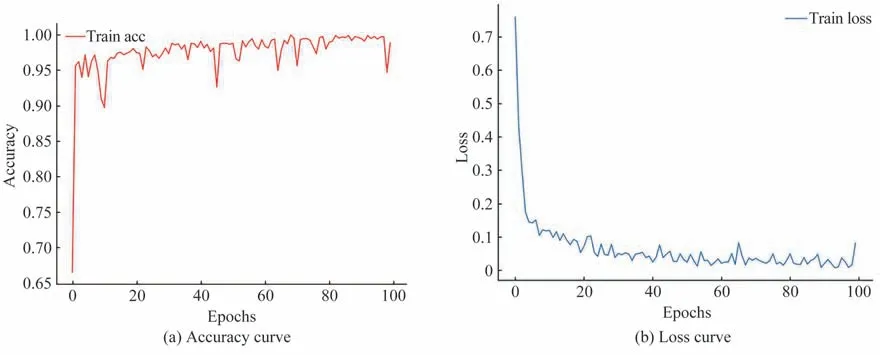
图10 实验数据集在该模型上的分类精度曲线和损失值曲线Fig.10 The classification accuracy curve and loss value curve of the experimental dataset on this model

实验中的湍流场控制和产生是通过调节加热棒的工作时间以及调整水下湍流传感器的位置来实现的。调节加热棒的内部温度和传感器的位置，可以调整水中湍流场的强度分布。由于激光具有强相干性，当受到湍流的影响后，其相干性会受到破坏，进而影响散射介质反射形成的干涉光路。

已知温差耗散率为［20］

式中，T0表示温度场的均值，Tw表示热源温度，KTx表示垂直方向上的湍流热扩散率，在无湍流情况下，将KTx取为10-7量级；而在有湍流情况下，将KTx取为10-3量级。从式（6）可以看出，温差耗散率与环境水温和热源温度之差成正比，即温差越大，耗散率越高。此外，随着空间距离的增加，温差耗散率迅速衰减。

利用建立的深度学习模型，将实验采集的散斑图像数据集输入该模型进行训练。训练过程中，分类精度曲线和损失值曲线如图10所示。可以看出，分类精度曲线和损失值曲线与图7 相比，分类精度收敛略慢，初始损失值增大了0.3，这说明在实际应用时存在一定误差，尽管如此，模型的效果仍然是相当不错的。随机选择10 张散斑图像数据，并通过模型进行验证。验证结果显示，模型的识别准确率达到100%，如图11所示，验证结果充分证明了模型的有效性。

图11 实验数据集在该模型上的分类精度曲线和损失值曲线Fig.11 The classification accuracy curve and loss value curve of the experimental dataset on this model

本文方法在实验采集数据集上对XT测量上的性能指标的实验结果，具体数据见表3 和图12。

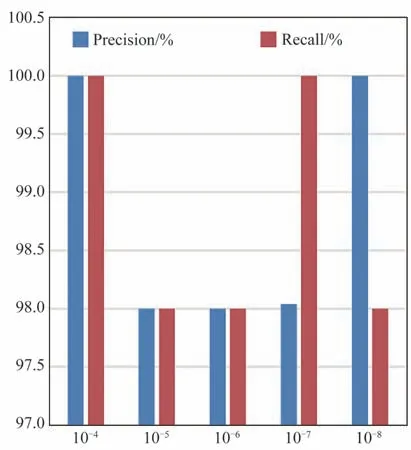
图12 实验数据集在该模型上的精确率和召回率方面的表现Fig.12 The performance of the experimental dataset in terms of accuracy and recall on this model

表3 实验数据集在该网络XT 测量上的性能指标Table 3 XT performance indicators of the experimental dataset in this network measurement

4 结论

提出了一种用于测量水下温差耗散率的卷积神经网络方法，并成功地验证了其有效性。采用相位屏法对水下湍流对激光束的扰动进行模拟，利用光场公式生成具有不同温差耗散率下的受到湍流影响的散斑图像数据集，将该数据集作为卷积神经网络的输入，并经过特征提取等操作，实现了对温差耗散率的准确测量。相比于ResNet 和Transformer 的结合模型，本文模型在训练过程中采用深度可分离卷积，从而提高了模型的稳定性和训练速度，同时也改善了模型的精度和泛化性能。通过在实验平台上的验证，我们发现该方法在测量水下温差耗散率方面取得了令人满意的结果，测量准确率高达98.8%。本文模型在水下环境中对温差耗散率的测量具有很高的可行性和有效性。