基于Kelvin模型的圆形巷道位移反分析的唯一性
2024-01-27张志增程一桐周林豪余浩然刘丰林
张志增,程一桐,周林豪,余浩然,刘丰林
(中原工学院建筑工程学院)
引 言
随着数值模拟技术在地下工程稳定性分析方面的应用日益广泛,对数值模拟结果产生较大影响的已经不是数值计算方法,而是岩体参数[1]。然而,由于岩体经历了数万年的复杂演变,不仅具有尺寸效应,还具有时间效应,确定其力学参数难度较大。
一般地,常用的岩体力学参数获取方法包括经验类比法、现场原位试验法与实验室试样试验法等,但各有不足[2-5]。例如:现场原位试验的结果固然可靠,却受到试验周期长、成本高等限制,如果将现场试验作为获取岩体参数的主要手段,其经济成本将远远超过允许的范围;实验室试样试验法在取样过程中已经改变了岩体的原始力学状态,加上样品尺寸有限,其代表性也值得进一步讨论。反分析法的问世,为岩体力学参数的确定指明了一条新道路[6-7]。
反分析法[8-10]是将现场量测数据作为已知条件,通过反演模型推算出岩体初始参量的求解方法,能够较为准确地反映岩土体的力学行为,在实际工程中得到了较为广泛的应用。谢建兵等[11]利用简易瑞典条分法对某露天矿滑移面的抗剪强度参数进行反分析;汤华等[12]基于均匀设计法反分析出小湾水电站地下硐室的相关物理力学参数;魏霖阳[13]论述了双硐室存在时反分析理论。
在位移反分析中,一个重要的问题是解的唯一性,忽略反分析的唯一性可能会使计算结果失去价值,但目前针对此领域的研究并不充分。吕爱钟等[14-15]推导了参数可辨识性条件,并论证了地下硐室弹性位移反分析的多种唯一性问题;张路青等[16]阐述了单一硐室位移反分析的唯一性;YANG等[17]用作图的方式证明了图谱反分析的唯一性;张志增等[18-20]对位移反分析的基础理论进行了若干研究;李小昌[21]考虑了剪应力对位移反分析唯一性的影响。以上文献的研究对象均为弹性介质,而理论研究和工程实践表明,大多数岩体都反映出与时间相关的黏弹性特征[22]。因此,对黏弹性岩体位移反分析唯一性的研究在指导工程实践、提高反分析的准确性方面有广泛用途。本文以前人的研究成果为基础,以Kelvin模型为基本流变模型,对黏弹性岩体中圆形巷道位移反分析的唯一性进行研究。
1 圆形巷道黏弹性解析解
圆形巷道计算模型如图1所示,在弹性岩体中开挖一个水平向的圆形巷道,并假设巷道埋深足够大,地应力场均匀,则围岩内任一点因开挖引起的径向位移(ur)[23]为:
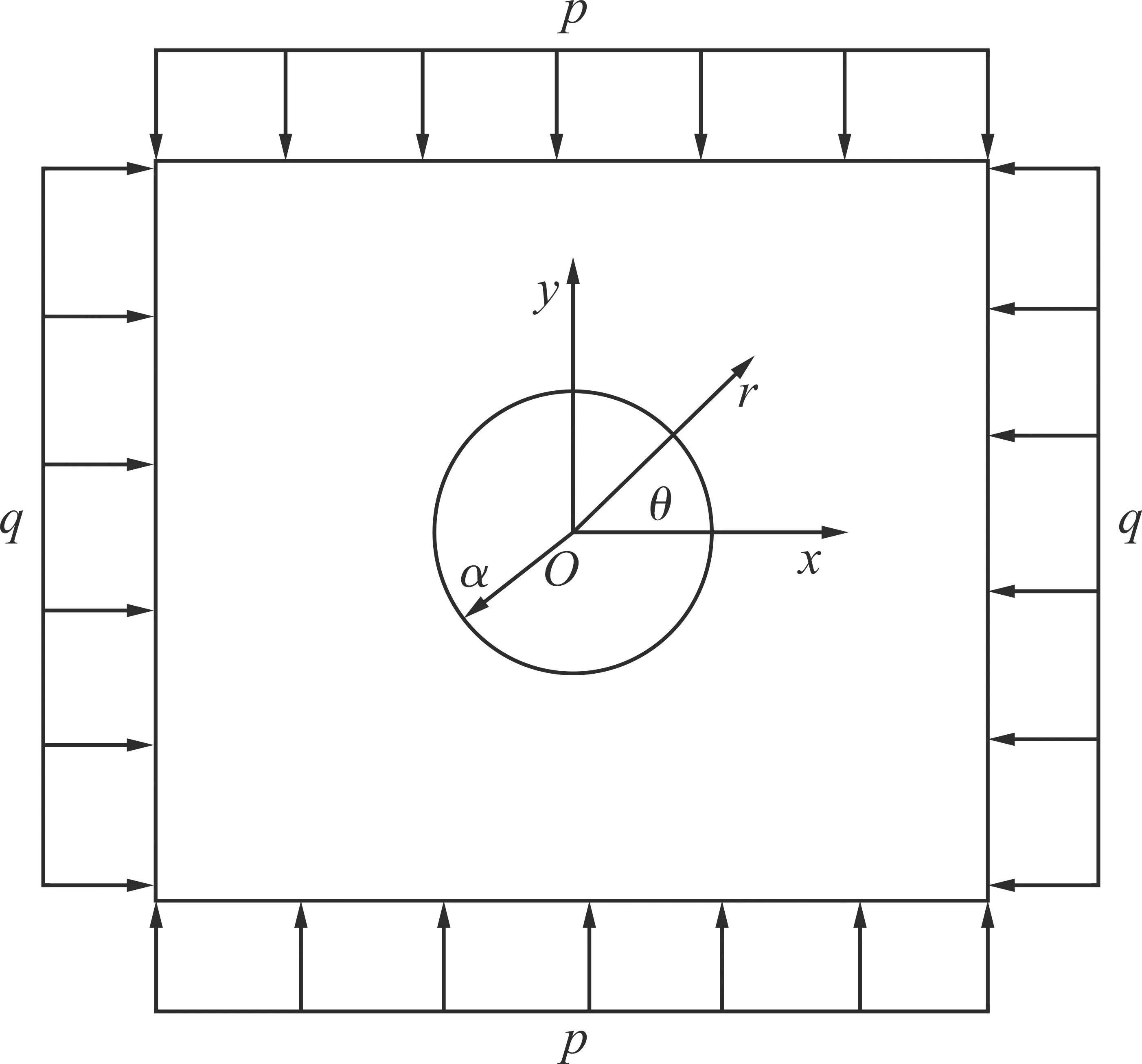
图1 圆形巷道计算模型Fig.1 Calculation model of circular roadway

(1)
式中:μ为泊松比;E为弹性模量(MPa);p为竖直方向的地应力(MPa);a为巷道的半径(m);q为水平方向的地应力(MPa);r为围岩内任一点至巷道中心的距离(m);θ为该点径向与水平向的夹角(°)。
令
(2)
(3)
将式(1)改写为:
(4)
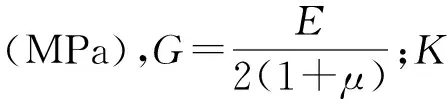
黏弹性岩体介质的本构方程f(D)σ为:
f(D)σ=g(D)ε
(5)
Kelvin模型的微分本构方程σ为:
(6)

则拉式空间下Kelvin模型的微分算子形式为:
(7)
由此得到Kelvin模型的蠕变柔量J1(t)与广义蠕
变柔量J2(t)[24]为:
(8)

(9)

对式(4)进行Laplace变换得到圆形巷道黏弹性径向位移表达式:
ur(t)=ArJ1(t)+BrJ2(t)
(10)
将式(2)、式(3)、式(8)、式(9)代入式(10),得到符合Kelvin本构模型的黏弹性岩体在圆形巷道下的位移解析解:
(11)
2 位移反分析的唯一性
2.1 判定准则
位移反分析的唯一性可用式(12)所示的参数可辨识法则进行判别[10],∂fi/∂βj为待反演参数fi的灵敏系数,根据∂fi/∂βj的线性相关性来判别βj的可辨识度:若∂fi/∂βj线性无关,待反演参数能够唯一地被辨识,反之则不能唯一地被辨识。
(12)
式中:fi为位移输出值;β1,β2,…,βj为待反演参数;n为测点的数目,n≥j。
当式(12)成立时,至少存在一个不等于0的Cj,此时灵敏系数线性相关;反之,当且仅当Cj等于0时式(12)才成立,此时灵敏系数线性无关。
将各参数的灵敏系数代入式(12),整理得到:
(13)
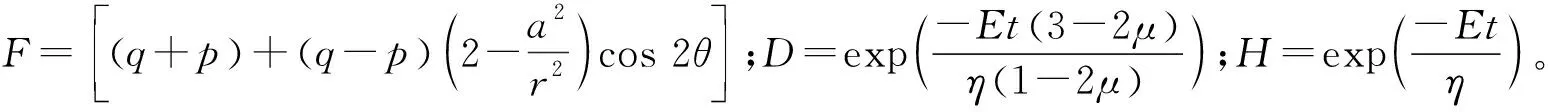
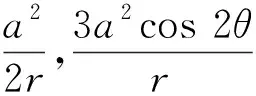
(14)
相应的系数矩阵为:
(15)
方程组(14)中有5个未知数,3个方程,所以最少要已知2个参数,其他参数才有可能唯一地被反分析出来,否则,无论增加多少测量点,都不能把所有参数唯一地反分析出来。为使反分析结果更加通俗明了,在此引入如下概念:
1)不唯一,指当各参数之间满足任意条件时,反分析的结果都不唯一。
2)条件唯一,指当各参数之间满足某种条件时,反分析的结果才唯一。
3)绝对唯一,指各参数之间无论存在何种条件,反分析结果都唯一。
2.2 已知任意2个参数时的情况
假设已知竖向地应力p与水平地应力q,反分析E、η与μ3个参数,此时∂ur/∂p、∂ur/∂q应为0,此时的系数矩阵为:
(16)
待反演参数灵敏系数的线性相关性可用系数矩阵的秩R来判断,矩阵满秩的情况下,线性方程组(14)只存在0解,灵敏系数线性无关,反分析唯一;否则,灵敏系数线性相关,反分析不唯一。矩阵(15)的秩R=2<3,属于反分析不唯一的范畴。其余反分析结果及其充分条件如表1所示,每个参数都被反分析了6次,结果如表2所示。根据表1、表2中的数据,可以得到以下结论:

表1 已知2个参数时的反分析唯一性Table 1 Back analysis of uniqueness for the case of 2 known parameters

表2 已知2个参数时的反分析结果统计Table 2 Statistics of back analysis of results for the case of 2 known parameters
1)在已知任意2个参数的条件下,反分析不唯一的情形只有1种,条件唯一的情形有9种。
2)地应力显著影响了反分析的结果,2个方向的地应力作为已知量且不等于0时,反分析结果唯一;二者不相等时,反分析结果唯一。
3)参数p与q的可辨识性最好,μ、E与η次之。
2.3 已知任意3个参数时的情况
假设已知竖向地应力p、水平地应力q与黏滞系数η,反分析E、μ2个参数,此时,∂ur/∂p、∂ur/∂q和∂ur/∂η都应为0,此时的系数矩阵为:
(17)
2个方向的地应力相等时,矩阵(17)的秩R=1,反分析不唯一;不相等时,矩阵的秩R=2,反分析唯一。其余反分析结果及其充分条件如表3所示,每个参数都被反分析了4次,结果如表4所示。根据表3、表4中的数据,可以得到以下结论:

表3 已知3个参数时的反分析唯一性Table 3 Back analysis of uniqueness for the case of 3 known parameters

表4 已知3个参数时的反分析结果统计Table 4 Statistics of back analysis of results for the case of 3 known parameters
1)在已知任意3个参数的条件下,绝对唯一有4种,条件唯一有6种,不存在不唯一的情况。
2)地应力对结果的影响同样明显,在2个方向的地应力作为已知量且相等时,反分析结果不唯一;二者不相等时,反分析结果唯一。
3)参数p的辨识性最好,q、E次之,η与μ最差。
2.4 已知任意4个参数时的情况
假设已知竖向地应力p、水平地应力q、黏滞系数η与弹性模量E,反分析泊松比μ。此时∂ur/∂p、∂ur/∂q、∂ur/∂η与∂ur/∂E都应为0,即方程组(14)中含有C1、C2、C3与C4的项都为0,此时的系数矩阵为:
(18)
当地应力相等时,上述矩阵为0矩阵,反分析结果不唯一;当地应力不相等时,反分析结果唯一。
其余反分析结果及其充分条件如表5所示,每个参数均被反分析了1次,结果如表6所示。根据表5、表6中的数据,可以得到以下结论:

表5 已知4个参数时的反分析唯一性Table 5 Back analysis of uniqueness for the case of 4 known parameters

表6 已知4个参数时的反分析结果统计Table 6 Statistics of back analysis results for the case of 4 known parameters
1)在已知任意4个参数的条件下,绝对唯一的情形有4种,条件唯一的情形有1种。已知条件增多,各参数的可辨识性明显增强。
2)较于前两种情况(已知任意2个参数,已知任意3个参数),地应力之间的关系对反分析结果的影响逐渐降低。
3)参数p、q、η与E的可辨识性较好,μ较差。
3 待反分析参数的数量对唯一性的影响
黏弹性岩体的位移解析解较为复杂,以至于求解系数矩阵存在一定难度,且参数的可辨识性表现不太理想,绝对唯一的情况只占少数。在实际工程中,通过位移反分析将所有的岩体参数都反分析出来,既缺乏可能性,也缺乏必要性。所以位移反分析的工作要点要放在对地下工程影响较大或通过常规手段难以确定的参数上。在本文反分析的5个参数中,泊松比μ的影响相对来说不如其余4个参数重要,因而可以考虑将其排除在外从而提高其余参数的唯一性。若不将泊松比作为已知参量,此时线性方程组对应的系数矩阵为:
(19)
矩阵(19)的秩为3,共有4个未知数,至少已知1个参数,才有可能反分析出其余参数。按照上述分析方法进行反分析,结果如表7~9所示。
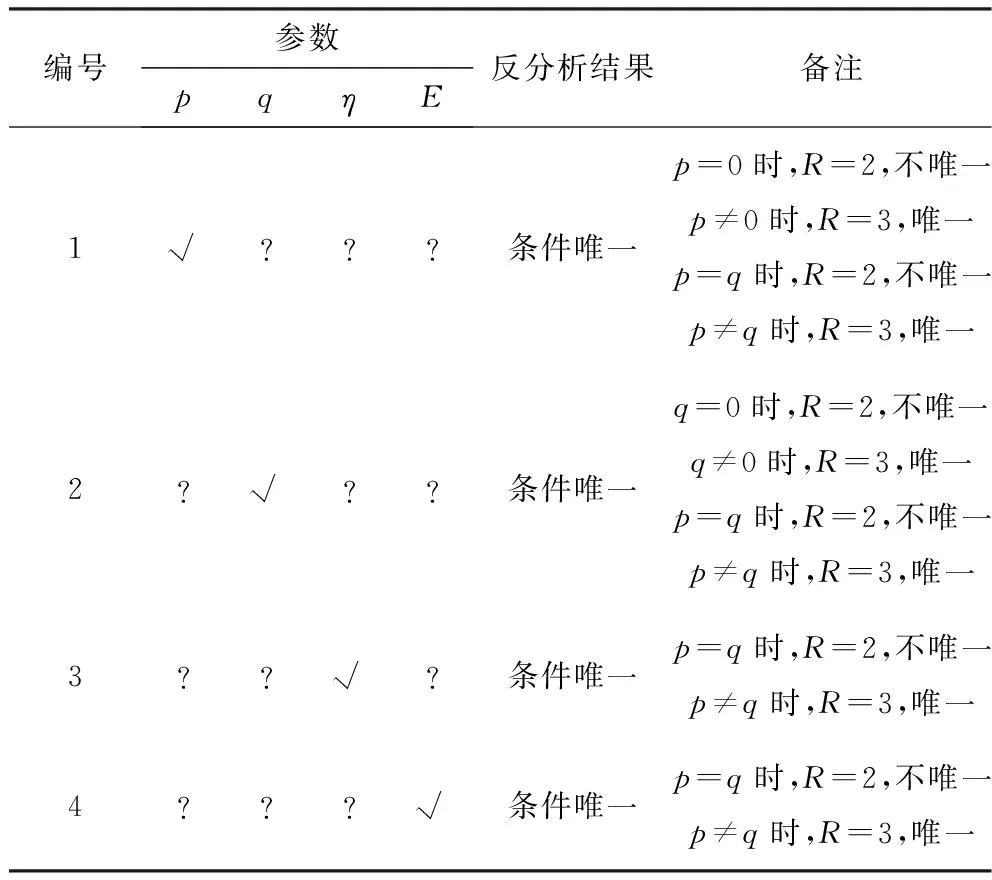
表7 已知1个参数时反分析的唯一性Table 7 Back analysis of uniqueness for the case of 1 known parameter

表8 已知2个参数时反分析的唯一性Table 8 Back analysis of uniqueness for the case of 2 known parameters
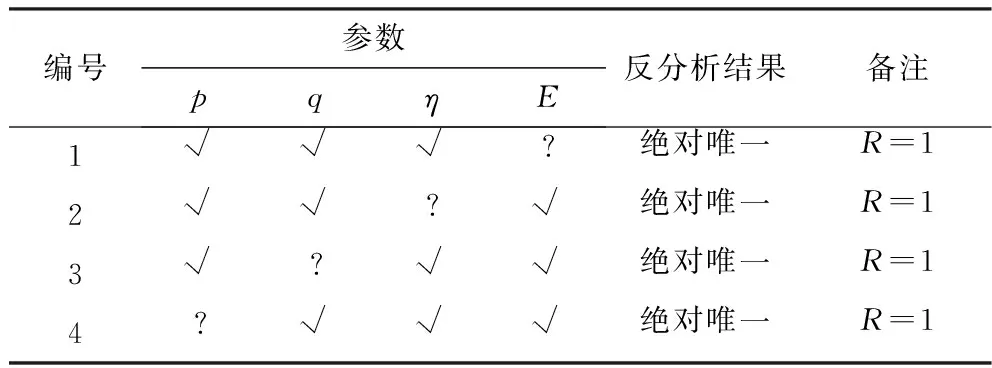
表9 已知3个参数时反分析的唯一性Table 9 Back analysis of uniqueness for the case of 3 known parameters
从反分析结果可以看出,在不考虑泊松比的前提下,其余参数的可辨识性均有提升。在所有的反分析结果中,前提唯一的情况占比从64%降低到35.7%,绝对唯一的情况占比从32%提高到64.3%,不存在不唯一的情况。
综上所述,对待反分析参数进行合理的取舍,不仅可以降低工作量,对提高参数可辨识性也有很大帮助。
4 结 论
1)讨论了3种情形(已知2个参数、已知3个参数和已知4个参数)下符合Kelvin本构模型的黏弹性岩体位移反分析的唯一性。最少已知2个力学参数,其他参数才有可能唯一地被反分析出来,否则,无论增加多少根测线,都不能把所有参数唯一地反分析出来。
2)已知的参数越多,待反分析参数被辨识的可能性就越大。当未知参数较多时,各参数的可辨识性存在显著差距。2个方向的地应力是否已知、是否相等及是否为0对反分析结果的影响较为明显。
3)根据实际需要适当地选择待反分析参数,对提高反分析结果的唯一性有显著影响。
4)总体看来,地应力具有最好的可辨识性,其次是弹性模量、泊松比及黏滞系数最差。
