基于灰狼算法改进随机森林算法的爆破振动速度预测研究
2024-01-27胡学敏宋良灵
胡学敏,曾 晟,宋良灵
(1.南华大学资源环境与安全工程学院; 2.湖南有色金属职业技术学院资源环境系; 3.南华大学土木工程学院)
引 言
爆破开采方式因其所带来的经济性和高效性,而被广泛地应用于露天矿山开采。而爆破作业产生的能量大部分会转化为爆破应力波,通过岩石等介质向更远处传播,对邻近建筑物造成不利影响[1],其影响程度一般用质点振动速度来描述。因此,如何精确地预测爆破振动速度对露天矿山的安全开采具有重要的工程意义。
早期爆破振动速度预测一般采用萨道夫斯基、P.B.Attewell及J.R.Devine等经验公式,但这些经验公式都很难准确反映振动速度与爆破参数之间的非线性关系,且预测精度较低[2]。而人工智能算法能够很好地处理这种非线性关系[3-4],因此人工智能算法预测爆破振动速度得到广泛应用,随之单一人工智能算法,如BP神经网络[5-6]、支持向量机[7]、相关向量机[8]、遗传算法[9]、粒子群算法[10]等在爆破振动速度预测中得到应用。但是,这些单一算法存在很多缺点,如需要数量大且连续的样本、迭代次数较多、收敛速度较慢、运算速度较慢和准确性较低等。随着研究的深入,学者们提出组合算法来改善单一算法的不足。例如:范勇等[11]使用粒子群和神经网络组合对露天矿爆破振动速度进行研究分析,提出了PSO-BP的爆破振动速度峰值预测模型;何理等[12]使用粒子群和支持向量机组合对爆破振动进行预测;岳中文等[13]提出了基于PCA-GA-SVM的露天矿爆破振动速度预测模型;郭钦鹏等[14]构建了遗传算法和BP神经网络的组合算法,并用于露天矿爆破振动速度预测;郑皓文等[15]提出了基于ACOR-LSSVM算法的爆破振动速度预测模型。实践证明,组合算法能够提高爆破振动速度预测精度。
近年来,随着灰狼算法、布谷鸟算法、鲸鱼算法、萤火虫算法、随机森林算法、蚁群算法等仿生算法的出现,以及这些算法在实践工程研究中得到验证,也为爆破振动速度预测模型的改进和预测精度的提高提供了新的思路。实践表明:灰狼算法(Grey Wolf Optimizer,GWO)与其他仿生算法相比,具有搜索能力强、调节参数少、收敛能力较强等优点,随机森林算法(Random Forest,RF)具有准确率高、不容易出现过拟合、抗噪能力强、处理离散数据能力强等优点,通过结合2种算法各自的优点,提出了基于灰狼算法改进的GWO-RF爆破振动速度预测模型(GWO-RF预测模型),并将其应用至某露天开采矿山爆破工程实践中,实践证明该方法能很好地进行露天矿爆破振动速度预测。
1 GWO-RF预测模型建立
1.1 基本算法
1)GWO算法。因灰狼捕猎速度快,围猎动物能力较强,种群内有着严格的社会主导层级结构等特点,Mirjalili首次提出了新型群体仿生优化算法[16],即灰狼算法(GWO)。该算法通过模仿狼群的四层阶级制度来定义狩猎过程中的指挥命令优先级,头狼α>二级狼β>三级狼δ>普通狼ω。
灰狼群体的狩猎过程主要有3个阶段:第一阶段,通过侦察、追踪和寻找猎物,并不断靠近它;第二阶段,在头狼α的指挥下,从几个方向骚扰猎物,使猎物的活动范围逐渐减小,并形成包围,直至猎物无法逃脱,等待被捕;第三阶段,攻击猎物,灰狼与猎物之间是不断变化和寻找最优解的过程,灰狼围攻猎物的表达式见式(1),算法位置的更新图见图1。

图1 灰狼位置更新图Fig.1 Grey wolf position update diagram
(1)
式中:D为灰狼位置;XP(l)为狩猎位置向量;X(l)和X(l+1)均为XP(l)影响后的位置向量;l为迭代次数;lmax为最大迭代次数;A和C为变量系数;a为收敛因子(取值从2线性减少到0);r1和r2为0~1的随机参数。
狼群依次在头狼α、二级狼β、三级狼δ的领导下不断调整位置,并对被包围的猎物进行攻击。在每一次的迭代中,得出的最佳值都会分配给α、β及δ,普通狼会根据前面狼的位置调整自身位置,数学表达式见式(2)~(4)。
(2)
(3)
X(l+1)=(X1+X2+X3)/3
(4)
式中:X1、X2和X3为狼群中其他狼受影响后的移动方向,由α、β、δ狼控制。
结合式(1)得到狼群的最终移动方向,并迭代更新狼群的位置。当达到收敛时,狼群不再移动,狼的当前位置就是最优解。本文通过灰狼算法来寻找随机森林算法中的2个超参数:决策树的棵数和决策树的层数。这2个超参数的正确选择可以提高随机森林算法运算的准确性、速度等。
2)RF算法。随机森林算法的原理是通过使用Bagging法来随机有放回的抽取样本,把数据集抽取出N个子集,每一个子集就是一棵决策树,N棵决策树集合在一起运算叫作随机森林算法。单棵树使用不同参数进行逐级分类,选择好结点的参数是模型能否运行成功的关键,采用的方法是计算每一个参数所能带来的分类下降效果,常用C4.5算法来计算下降的效果,然后进行逐级递归。每一棵决策树都有一个结论,对N棵决策树取平均值来最终确定结果。本文采用组合的随机森林算法进行预测研究。具体算法为:①在原始数据集中进行N次Bagging法采样,每一次都是有放回的采样,得到了N棵决策树;②在决策树的算法中对每一个子集进行计算,得出一个结果;③用群智能算法的原理,对所有结果取平均值得出最后结果。具体算法见图2。
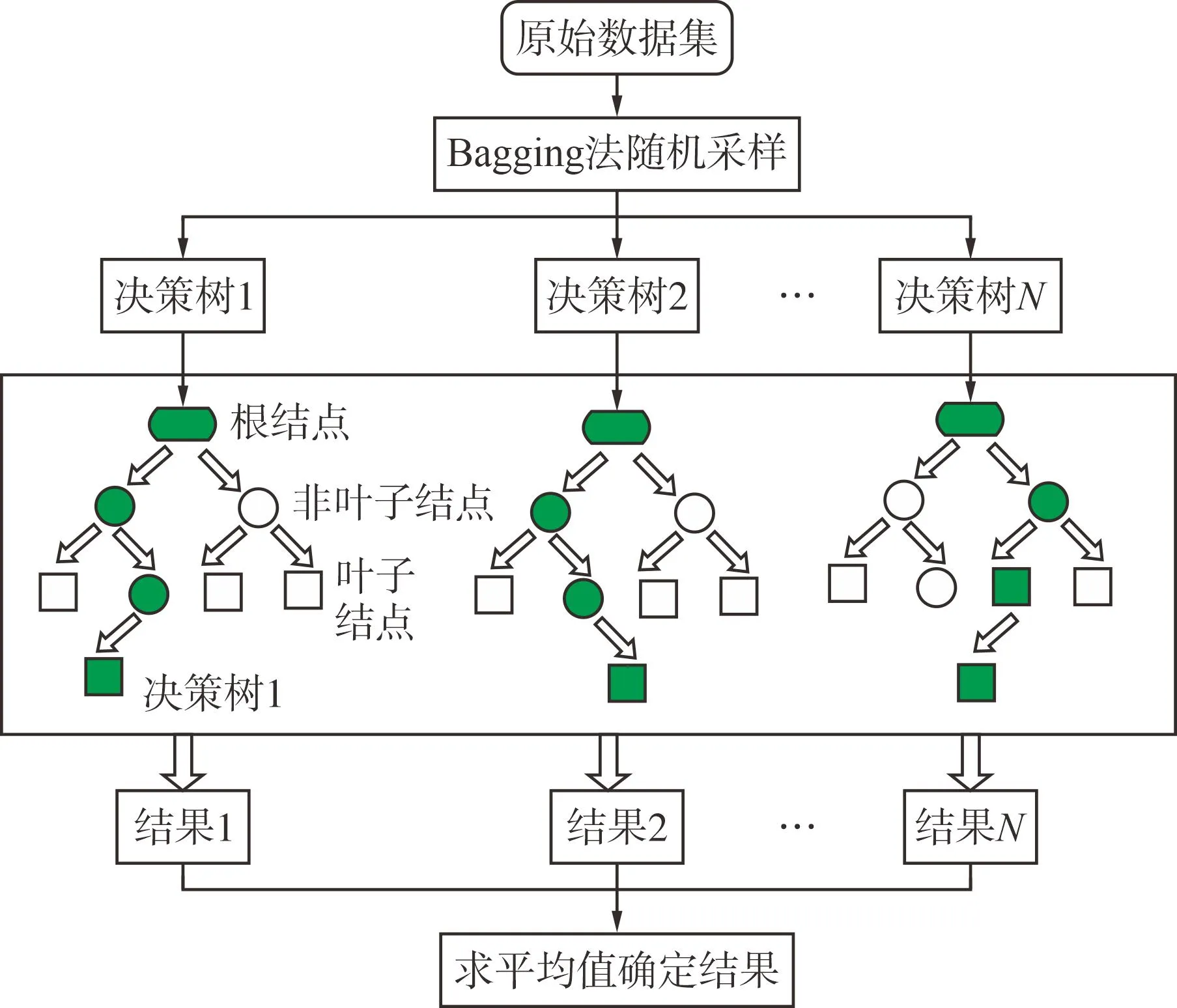
图2 随机森林算法流程图Fig.2 Random Forest Algorithm flow chart
1.2 GWO-RF组合算法
GWO具有非常好的全局优化能力和收敛能力。GWO-RF组合算法是采用GWO的优点寻找RF中的决策树的棵数和决策树的层数2个超参数,将其应用到爆破质点振动速度的预测中,具体的步骤(见图3)如下:
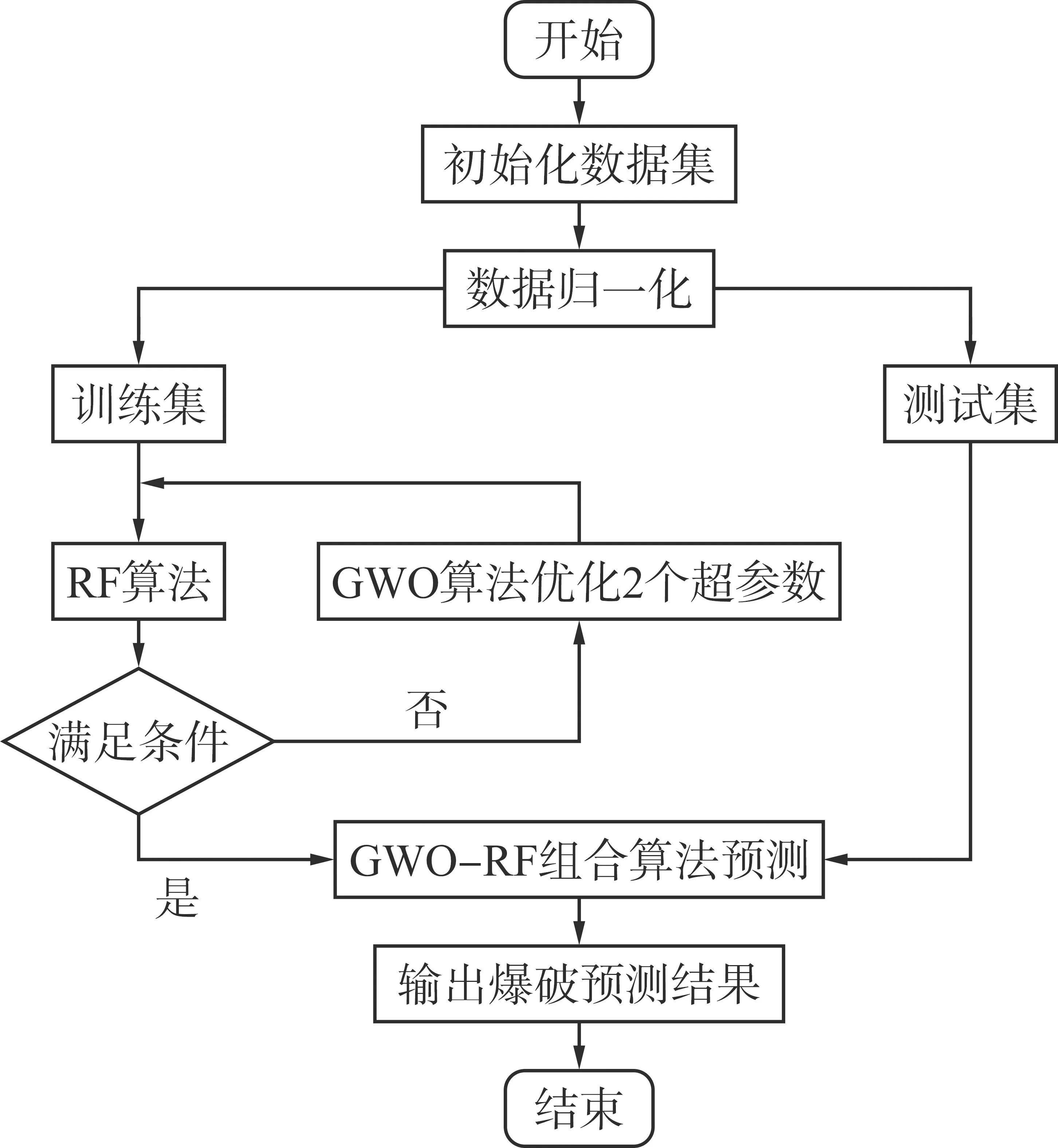
图3 GWO-RF组合算法预测流程图Fig.3 GWO-RF combined algorithm prediction flow chart
1)数据的处理。输入爆心距、微差时间、炮孔数、孔距、排距、孔深、总装药量及最大段药量至RF算法中。
2)初始化。初始化狼群Pi,即随机生成n个参数,表达式见式(5)、式(6):

(5)
(6)

3)计算适应度函数。为了确定狼群中每个个体的等级关系,有必要设置一个合理的适应度函数来量化个体的适应度,适应度函数f(P)为:
f(P)=J(U,P)
(7)
式中:J(U,P)为目标函数值,代表爆破振动预测的准确性。
4)更新狼群的位置后,按照适应度函数值排序,头狼α、二级狼β及三级狼δ按照式(1)~(6)更新狼群的位置。
5)函数收敛。在每次迭代后,都需要检查收敛的情况。如果已经收敛,则进入到下一步骤。否则,它将返回继续迭代。当狼群适应度值的离散度较低时,GWO的全局搜索能力开始下降,算法趋于收敛。因此,本文使用狼群适应度的方差作为标准。当方差小于阈值,算法收敛。
6)训练模型。根据最终狼位置得出超参数,然后设置RF模型参数,并执行RF算法以输出预测结果。
2 工程应用
2.1 GWO-RF预测模型预测
为检验GWO-RF预测模型的实际效果,依据某露天矿山爆破工程监测的69组爆破振动数据作为模型的检验样本,见表1。

表1 数据样本Table 1 Data sample
首先对69组数据进行归一化处理,选取训练样本62组数据输入RF模型并设置GWO算法的参数,如灰狼个数20、最大迭代20次,优化2个变量,取最大值100,设置起始适应度值为0.023 46,在第7次开始下降,适应度值为0.022 98,第10次收敛值为0.022 96,进行收敛后得到2个变量的最优值,GWO-RF组合算法收敛曲线见图4。此时决策树层数为6层,决策树棵数为14棵,目标函数值为0.012 4。

图4 GWO-RF组合算法收敛曲线Fig.4 GWO-RF combined algorithm convergence curve
2.2 预测结果
灰狼算法与随机森林算法的组合解决了如何设置最优参数的问题。当进行回归时超参数设置不合理会出现过度拟合,所以先使用灰狼算法寻找出以下2个超参数,然后将参数输入到随机森林模型中。经计算,预测值与真实值的平均误差为97.72 %,训练集与预测集的样本平均误差率为98.38 %,具体见图5、图6。
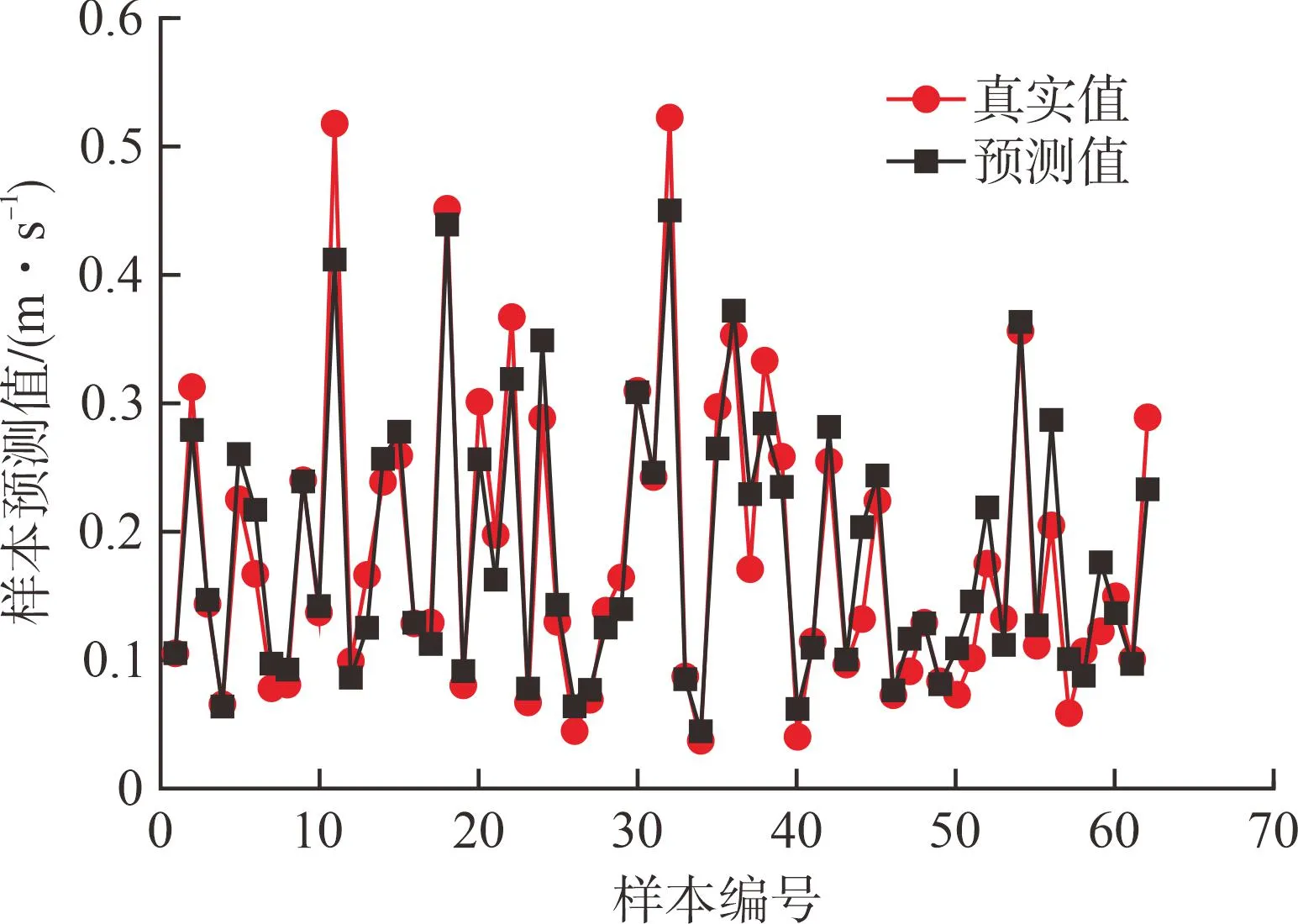
图5 GWO-RF训练集与预测结果对比Fig.5 Comparison of GWO-RF train set and prediction results

图6 GWO-RF预测集与预测结果对比Fig.6 Comparison of GWO-RF test set and prediction results
2.3 不同预测模型结果对比
原始数据、RF、GWO-RF组合预测数据的对比见表2,RF算法、GWO-RF组合算法的预测曲线见图7。由图7可知:RF算法的预测精度较差,平均误差率为59.89 %;GWO-RF组合算法误差率比RF算法提高了37.83百分点,这充分说明了使用GWO搜寻RF超参数比单一RF算法的预测精度高。

表2 预测结果与检验样本对比 m/sTable 2 Comparison of the prediction results and test samples
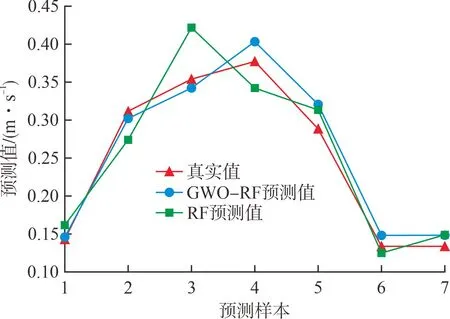
图7 2种方法预测结果对比Fig.7 Comparison of the prediction results of 2 methods
3 结 论
1)通过灰狼算法对随机森林算法的超参数进行优化,建立了GWO-RF爆破振动速度预测模型,为爆破振动速度预测提供了一种新途径。
2)GWO-RF预测模型解决了萨道夫斯基只考虑爆心距、最大段药量等参数的不足,还考虑了总装药量、微差时间、炮孔数、孔距、孔深及排距等6个参数,使得预测模型更加符合工程实际。
3)实践验证了GWO-RF预测模型对爆破振动质点峰值速度预测的预测精度为97.72 %,说明该预测模型具有可行性和较高的准确性,能够应用于爆破工程振动控制研究。
