具有Lévy跳的随机时滞食饵-捕食模型的最优收获

钟 颖, 韦煜明

(广西师范大学数学与统计学院,541004,广西壮族自治区桂林市)

0 引 言

近年来,全球生物多样性正在急剧下降,《地球生命力报告2020》中指出:全球物种数量在不到半个世纪的时间减少了约2/3.导致物种减少的重要原因之一是生物资源过度利用,在1992年,加拿大纽芬兰岛的渔民没有捕获到一条鳕鱼,由于过度捕捞导致4万人失去工作,该地区经济衰落.捕食与被捕食是自然界中普遍存在的种间关系,研究具有收获项的食饵-捕食模型具有重要的现实意义[1-4].随着研究的逐步深入,学者们发现时滞不可避免的存在于自然界中,比如妊娠时滞、成熟时滞、合作时滞等,研究发现时滞会引起系统的稳定性变化[5-8].在现实环境中,物种还会受到不同形式的随机因素干扰,比如温度变化、寒流、空气湿度变化等,此类数量多但强度小的干扰称为白噪声[9-13],同时也存在一些数量少但强度大的干扰,例如海啸、洪水、火山爆发等称为Lévy 噪声[14-16].随机扰动在自然界中无处不在,所以考虑随机噪声对种群动力学的影响是符合实际且必要的.

基于上述文献的启发,本文构建具有收获和时滞的随机食饵-捕食模型

(1)

1 平均持久性和灭绝性

为了方便讨论,给出下列记号和假设:

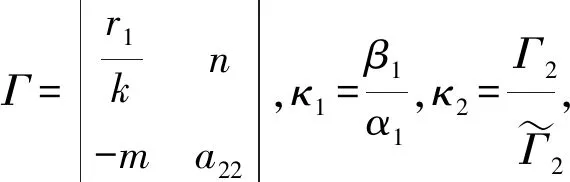
假设1 对于χi(u),1+χi(u)>0,u∈,t≥0,存在正常数D使得

假设2Γ1>0,Γ2>0.

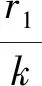
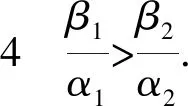
为了研究随机种群模型的动力学行为,首先要考虑它的解是否为唯一的全局正解,下面给出引理.

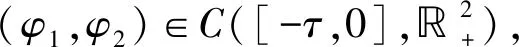
证明首先证明模型(1)有唯一的局部正解,考虑模型

(2)

接下来用比较定理[18]证明x(t)是全局解,即τe=+∞.考虑模型

(3)

初值yi(θ)=φi(θ),θ∈[-τ,0],i=1,2.由随机比较定理,当t∈[0,τe]有

xi(t)≤yi(t),a.s.,i=1,2.

(4)

根据文献[19]中的定理2.1,当t≥0时,模型(3)有唯一全局解y1(t),y2(t).因此得出结论τe=+∞.证毕.

引理1.2[20］假设函数f(t)∈C[Ω×[0,+∞],+],且假设1 成立.

(ⅰ)存在正常数T和λ0,当t≥T时,有

其中σi、λi(i=1,2)为常数,则

(ⅱ)存在正常数T、λ和λ0,当t≥T时,有

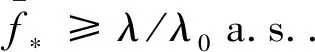
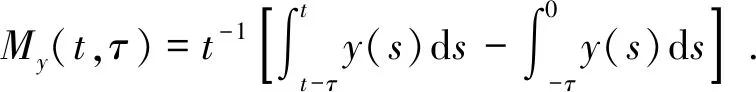
(5)

引理1.4 关于模型(3),有下列结论:

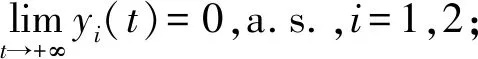
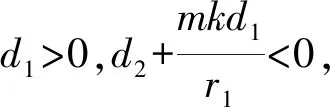
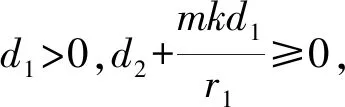
(6)

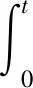
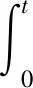
(7)

两边分别乘以t-1,得到

(8)

(9)

首先证明(ⅰ)成立. 由式(8)可推出

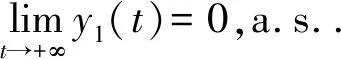
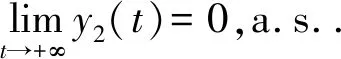
根据条件d1>0和引理1.2有

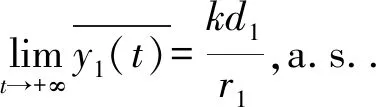
对于充分大的t,由式(9)得到

(10)

因此有

(11)

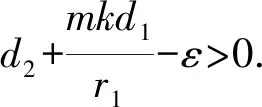
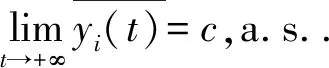
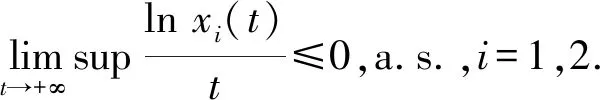
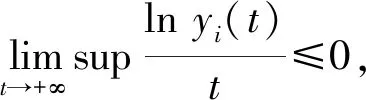
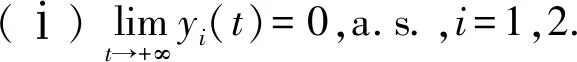
(ⅲ) 类似(ⅱ)的证明,故省略.

接下来,建立模型(1)中物种的时间平均持久性和灭绝性的充分条件.

定理1.1 对于模型(1),如果假设1-假设4成立,则κ1>κ2并且有下述结论:

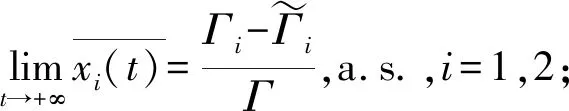
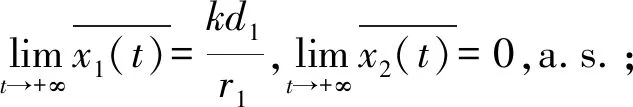
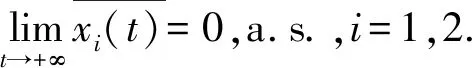
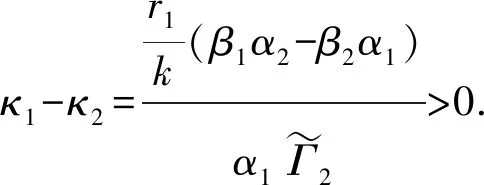
(12)

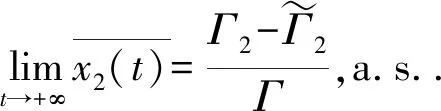
(13)

(14)

Δ1Δ2Mx1(t,τ1)+Δ1nMx2(t,τ2).

(15)

将上述两个不等式代入式(15),对充分大的t,有

(16)

由引理1.2中的(ⅱ)及ε的任意性,有

(17)

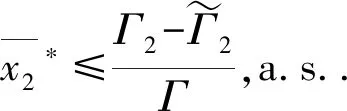
根据推论1.1,对于充分大的t,

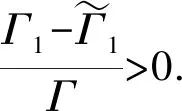
(18)

结合引理1.3推出

(19)

由引理1.2中的(ⅰ)及ε的任意性,有

(20)

根据引理1.3和式(20),得

(ⅱ) 由推论1.1、引理1.5和式(15),可以得到

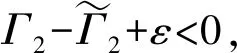
(ⅲ) 由条件知κ1<1,故有d1<0,通过引理1.4和式(4) 可以得到

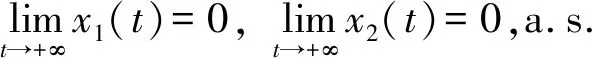
2 依分布稳定性

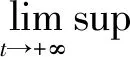
证明证明过程参考文献[22].

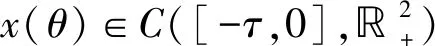
证明分3步证明定理2.1.

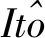
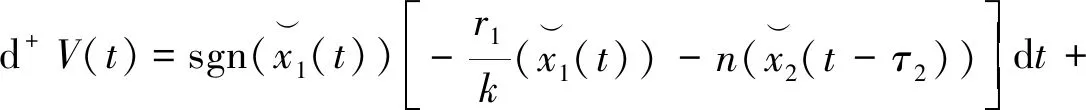
因此

(21)

≤r1(x1(t))≤r1c1,

其中c1是常数,因此(x1(t))是一致连续的.用同样的方法证(x2(t)) 是一致连续的.由Barbalat’s引理[23]和式(21)得到

(22)

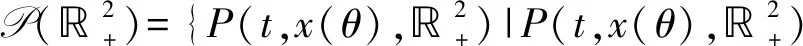
对于任意的P1、P2∈P,定义度量

其中D={h:2→对任意的h∈D和t,s>0有

|h(x(t+s;x(θ)))-h(x(t;x(θ)))|

=|[(h(x(t+s;x(θ)))|Fs)]-h(x(t;x(θ)))|

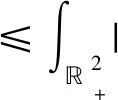
(23)

由式(22),存在T>0,当t>T时,有

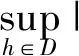
(24)

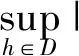
对任意的t≥T,s>0有dD(P(t+s;x(θ),·),P(t;x(θ),·))≤ε.

(25)

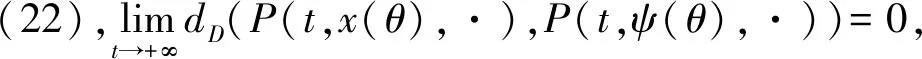
3 最优捕捞策略

本节研究模型(1)的最优捕捞策略,建立最优捕捞策略存在的充分条件.

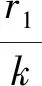
定理3.1 当假设1-假设3成立时,定义L=(r1-α1,r2-α2)T,A=(λ1,λ2)T=[Q(Q-1)T+I]-1L,其中I为单位矩阵.

(ⅰ) 如果κ2>1,λi≥0,i=1,2,则最优捕捞策略(OHE)存在且OHE为H*=A,最大可持续产量(MESY)为Y*=ATQ-1(L-A).

(ⅱ) 若(ⅰ)不成立,则模型(1)的最优捕捞策略不存在.

证明令G={H=(h1,h2)T∈2|κ2>1,hi≥0,i=1,2}.显然H∈G,由定理1.1中的(ⅰ),如果H*存在,那么H*∈G.

(ⅰ) 显然A∈G,因此G非空.由定理2.1知,模型(1)有唯一的不变测度μ(·),通过文献[24]中的定理3.2.6得到μ(·) 是遍历的,由文献[24]有

且μ(·)是强混合的(见文献[24]中的推论3.4.3). 令ρ(x)表示模型(1)的平稳概率密度,因此

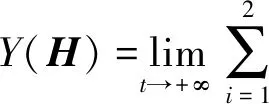
通过定理1.1,对任意的H∈G,有

注意到模型(1)的不变测度的是唯一的,因此由ρ(x)和它的不变测度的一一对应关系可得

故有Y(H)=HTQ-1(L-H).

令A=(λ1,λ2)T是下列方程(26)的唯一解,

(26)

因此A=[Q(Q-1)T+I]-1L.由于Hessian矩阵

=-(Q-1+(Q-1)T)

是负定的,因此A是Y(H)的唯一极值点.由此可得出结论:如果A∈G,则H*=A,且MESY为Y*.

4 数值模拟

在本节中,通过数值模拟验证模型(1)的理论分析结果.部分参数选自文献[25],根据模型的生物学意义估计剩余参数.文献[25]忽略了种群会受到人为捕捞,本文分别考虑了Lévy噪声和白噪声对最优捕捞策略的影响.令r1=0.7,h1=0.1,r2=-0.2,h2=0.05,k=1.4,n=0.4,m=0.3,a22=0.5,τ1=1,τ2=0.8.

(1)物种的持久性和灭绝性

本部分设置参数σ1=0.1,σ2=0.1.

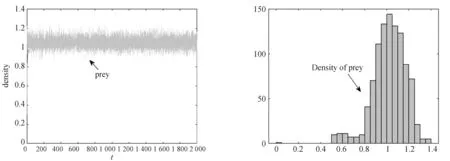
图1 x1的时间序列图(左图)和密度函数图(右图)

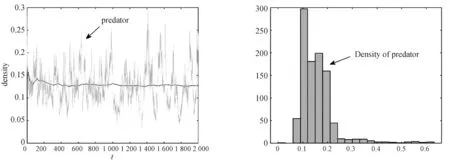
图2 x2的时间序列图(左图)和密度函数图(右图)

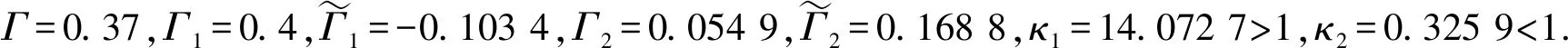
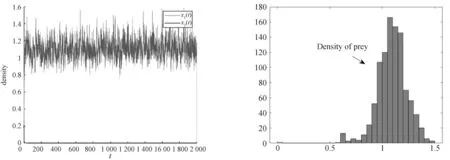
图3 种群的时间序列图(左图)和x1的密度函数图(右图)

图4 种群的时间序列图

(2)最优捕捞策略

分别对白噪声和Lévy跳噪声的强度取不同的值,观察种群的最优捕捞的变化.

(ⅰ)Lévy跳噪声对最优捕捞策略的影响.设置参数σ1=0.1,σ2=0.1.令χ1(u)=0.2,χ2(u)=0.15,计算得到κ2=3.813 4>1,H*=(0.297 3,0.325 3)T,Y*=0.236 3.令χ1(u)=0.4,χ2(u)=0.25,计算得到κ2=1.060 9>1,H*=(0.278 6,0.301 3)T,Y*=0.204 9.如图5所示.

图5 Lévy跳对最优捕捞策略的影响

(ⅱ)白噪声对最优捕捞策略的影响.设置参数χ1(u)=0.2,χ2(u)=0.1.令σ1=0.2,σ2=0.15,计算得到κ2=1.507 4>1,H*=(0.289 5,0.319 6)T,Y*=0.226 3.令σ1=0.35,σ2=0.3,计算得κ2=1.060 9>1,H*=(0.279 4,0.289 4)T,Y*=0.196 8.如图6所示.

5 结论与展望

本文研究了一类同时受到时滞、白噪声和Lévy跳随机扰动的食饵-捕食模型.定理1.1建立了物种时间平均持久和灭绝的充分条件,定理2.1和定理3.1探究了模型(1)的分布稳定性和最优捕捞策略.定理3.1表明最优捕捞策略与时滞无关,而环境波动的强度会影响种群:白噪声强度越大OHE和MESY越小,Lévy跳噪声强度越大,种群相应的OHE 和MESY 也越来越小.因此环境扰动会增加种群灭绝的风险.

在本文中,只考虑了时滞是常数的情况,还可以考虑连续分布时滞对模型的影响,或者考虑S型分布时滞,它包含了离散和连续分布时滞,建立更现实的模型进行研究.另外在现实环境中种群还会受到电报噪声的扰动,用马尔可夫过程描述,可以考虑在模型(1)中加入电报噪声,建立更复杂的模型进行更加深入的研究.