马尔可夫跳变系统的奇异自适应滑模控制
2024-01-26张秦诚魏云亮任帅帅
张秦诚, 魏云亮, 任帅帅
(曲阜师范大学数学科学学院,273165,山东省曲阜市 )
0 引 言
自上世纪六十年代以来,由于马尔可夫跳变系统在工程系统中的广泛应用,使得关于马尔可夫跳变系统的研究受到越来越多的关注,与此类系统相关的鲁棒稳定性、H∞控制等问题已有大量的成果得到发表. 例如,在文献[1]中首次提出了马尔可夫跳变系统的相关理论. 在文献[2]中提出了受执行器影响的马尔可夫跳变系统的鲁棒控制问题;H∞控制也在文献[3]中得到应用. 文献[4-7]中也都体现了马尔可夫跳变系统的理论成果. 同时,马尔可夫跳变系统的切换率又依据其跳变参数. 对于跳变参数已知、部分已知或完全未知的研究也是一个热点话题. 文献[8,9]等文章都涉及到了该话题的研究.
另一方面,对生物系统、工程系统、经济系统等实际系统的建模通常应用奇异系统来描述. 随着现代控制理论的不断完善与发展,奇异马尔可夫跳变系统的研究也逐渐成为一个热点话题,取得了不少相关的理论成果. 例如在文献[10]中给出了奇异马尔可夫跳变系统随机容许的条件. 文献[11] 针对不同的扰动类型提出了奇异马尔可夫跳变系统的复合控制方法. 针对状态不可观测以及多重扰动存在的情况,文献[12]给出了基于扰动观测器的复合分层抗干扰控制. 文献[13]也给出了奇异马尔可夫跳变系统的一些定义及理论成果.
此外,作为一类有效的控制方法,滑模控制方法的优势之处在于对参数变化和外部扰动具有出色的鲁棒性. 在很多文献中提出了应用滑模控制方法来确保在扰动存在的情况下马尔可夫跳变系统的稳定性. 例如在文献[14]中提出了滑模控制方法来考虑在匹配扰动存在的情况下马尔可夫跳变系统的稳定性问题. 在文献[15]中处理了随机马尔可夫跳变系统的滑模控制问题. 文献[16-18]也给出了滑模控制在切换系统上的理论成果. 然而,需要补充的是,应用的滑模控制器所要达到的结果只是针对理想的情况,在实际的控制系统中,由于系统参数变化、外部干扰以及检测技术的限制等因素的影响,通常使得滑模控制系统难以到达理想的效果,也就是说仅仅通过施加滑模控制来实现系统的目标性能,在一定程度上这会存在不可避免的保守性,因此需要将滑模控制与其他控制方法相结合来满足预期的系统性能. 自适应滑模控制便是一种很好的方法,能有效地达到目标要求. 文献[19]便通过鲁棒自适应非奇异终端滑模控制方案解决了列车自动运行系统的位置和速度追踪问题;针对不确定非线性切换系统,文献[20]给出了非线性马尔可夫跳变系统基于观测器的自适应滑模控制策略.
本文考虑了转移速率不完全已知的、具有匹配非线性和匹配外部扰动的马尔可夫跳变系统的奇异自适应积分滑模控制问题. 其中,非线性和外部扰动满足一定的假设条件且转移速率矩阵中的未知项不需要具体的信息. 首先按照奇异系统方法构造积分型滑模面,根据滑模动力学和原系统,可将原系统转化为奇异马尔可夫跳变系统. 接下来,以线性矩阵不等式的方法给出了一个定理来保证所得奇异马尔可夫跳变系统的随机容许性,再在这一定理的条件下设计自适应滑模控制来保证状态轨迹对滑模面的可达性.
文章的章节安排如下:第一部分给出了问题描述;第二部分给出了文章的主要结果,主要分为奇异马尔可夫跳变系统随机容许的定理及其证明过程,以及系统状态轨迹可达性的分析;论文的仿真结果体现在第三部分;第四部分对论文的成果进行总结.
1 问题描述
考虑定义在概率空间 (Ω,F,P) 上有如下形式的马尔可夫跳变系统
(1)
其中x(t)∈n,u(t)∈m,f(x,t)∈m,ω(t)∈m分别定义为系统的状态向量,控制输入,未知非线性函数和未知外部扰动.A(rt)∈n×n,B(rt)∈n×m是具有合适维数的常数矩阵. {rt,t>0} 是表示系统模态的有限状态马尔可夫过程,且它在l={1,2,…,N} 上取值. 令Π=(λij)N×N(i,j=1,2,…,N) 表示系统的转移速率矩阵. 则模态转移速率可表示为

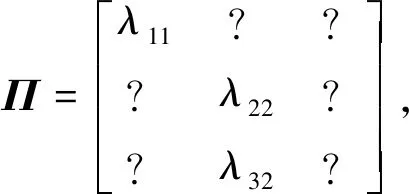
注1在实际工程应用中,转移速率完全已知的情况很难实现,且相较而言考虑转移速率部分已知是更为经济节能的一种方法;另外当系统转移速率完全已知时,所研究的即为传统意义下的马尔可夫系统,当转移速率完全未知时,代表的则是任意切换下的切换系统,因此研究转移速率部分已知的情况更具一般性.
为书写的简便性,当系统运行到第i个模态时,可将马尔可夫跳变系统 (1) 重新改写为
(2)
此外,为了进一步的讨论,需做以下假设:
假设1非线性函数f(x,t) 满足条件‖f(x,t)‖≤α+β‖x(t)‖,其中α>0、β>0是未知常数.
假设2匹配扰动ω(t) 是一有界向量,且其满足条件‖ω(t)‖≤ω,其中ω是未知的标量.
假设3对于任意的i∈l, 输入矩阵Bi列满秩.
接下来,将积分型滑模面函数设计为
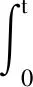
(3)
式中的Ki∈m×n是要设计的滑模控制器中的实矩阵,其可在接下来的定理2.1中求得. 矩阵Gi∈m×n要满足GiBi是非奇异的. 另选一行满秩的矩阵Mi∈(n-m)×n, 使得MiBi=0, 按奇异系统的方法选择矩阵Φi满足
(4)
式(4)中对任意的i∈l,Φi∈n×n是非奇异的. 接着,将原系统 (2) 左乘式 (4) 有
(5)
而考虑到已假设的MiBi=0, 则式 (5) 可化为
由于滑模面上满足s(t,i)=0 一式,且根据文献 [23] 中对滑模动力学理论的描述,则可得滑模动力学系统方程
(6)
接着可将式 (6) 继续化为
(7)

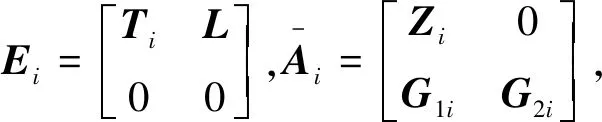
(8)
其中r(Ei)=r. 同时式(8)可看作由奇异系统方法转化成的奇异马尔可夫跳变系统.
下面将给出后文需要用到的定义以及引理.
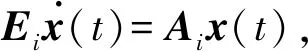
(1) 对任意的i∈l, 若 det(sEi-Ai)≠0, 则上述奇异马尔可夫跳变系统是正则的.
(2) 对任意的i∈l, 若 deg(det(sEi-Ai))=rank(Ei), 则上述奇异马尔可夫跳变系统是无脉冲的.
(3) 对任意的x0∈n,r0∈l,若ε{‖x(t,x0,r0)‖2}dt<+∞,则上述奇异马尔可夫跳变系统是随机稳定的.
(4) 若上述奇异马尔可夫跳变系统正则、无脉冲、随机稳定,则它是随机容许的.
引理1.1[10]若存在一个非奇异矩阵Pi, 对任意的i∈l有以下式子成立
引理1.2[21]若存在矩阵Xi>0,以及矩阵Yi、Ui、Wi使得对于任意的i∈l,有以下不等式成立
(9)
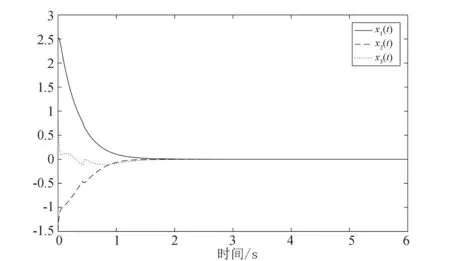
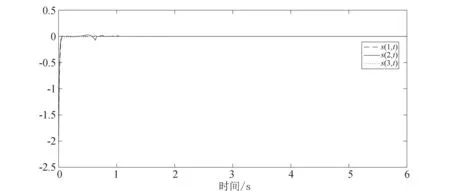
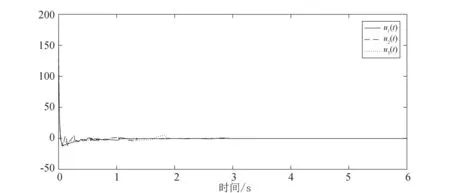
引理1.3[22]令ϖ是一对称矩阵,Γ、Ξ是具有合适维数的矩阵,矩阵Δ满足ΔTΔ ϖ+ΓΔΞ+ΞTΔTΓT<0 在这一部分中,定理 2.1 中提出了一系列线性矩阵不等式来保证奇异马尔可夫跳变系统 (8) 的随机容许性. 在定理 2.2 中,通过给出自适应滑模控制器u(t), 来确保任意模态下马尔可夫跳变系统状态轨迹的可达性. 定理2.1若存在矩阵X1i,Q1i∈(2n-m)×(2n-m);X2i,Q2i∈(2n-m)×m;X4i,Q4i∈m×m;Yi∈(2n-r)×(2n-r),Qi是对称的,以及Ki, 使得对 ∀i∈l, 有以下线性矩阵不等式 (10)~(13) 成立,则可以称具有部分已知转移速率矩阵的奇异马尔可夫跳变系统 (8) 是正则、无脉冲、随机稳定的(随机容许的): (10) (11) (12) (13) 其中 (14) 接下来,首先考虑矩阵不等式 (11),对其应用 Schur 补可得 基于引理 1.3 得 经展开,并记 Fi=F1i+F2i, (15) 可将Fi分解得到 (16) 注意到 则式(16) 可以化简为 (17) 则转移速率矩阵部分已知的奇异马尔可夫跳变系统 (8) 是随机容许的. 定理得证. 定理2.2对任意的i∈l,Ki满足定理2.1中的条件,则在自适应滑模控制律u(t) 的作用下,系统(2)的轨迹将在有限时间内到达滑模面上,并在之后的时间内保持在其上. 其中 (18) 上述3项自适应律设计为 以上cα、cβ、cω是需要设计的正实数,γ1为微小正常数.另外上述Di满足 (19) 证明选择下述形式的 Lyapunov 函数 则函数V(t) 沿着系统 (2) 轨迹的弱无穷小算子为 (20) 将式(2)、(3)、(18)和(19) 代入式 (20) 得到 LV(t)=sT(t)(GiBi)-1[GiAix(t)+GiBi(u(t)+f(x,t)+ω(t))-GiAix(t)-GiBiKix(t)]+ (21) 由于sT(t)sign(s(t))=|s(t)|≥‖s(t)‖,并考虑假设1和假设 2,则式 (21) 可以化为 ≤-(Di-Hi)‖s(t)‖2-γ1‖s(t)‖, 注2在研究的目标系统中尽管存在不完全已知的转移速率,但是可以通过选取一个适当的常数Di, 使得式 (19) 中不等式Di-Hi≥0 得到满足,从而尽可能减少转移速率部分已知这一情况对结果的干扰. 在本节中,我们将给出数值例子来验证所得结果的有效性. 考虑带有下列参数的马尔可夫跳变系统. 模态1: 模态2: 模态3: 则可得矩阵G(i): 通过定理2.1可求得矩阵K(i): 图1 切换信号轨迹 图2 闭环系统的状态响应轨迹 图3 滑模面的轨迹 图4 α(t)的估计值 图5 β(t)的估计值 图6 ω(t) 的估计值 图7 控制信号的轨迹 注3本文首次研究了转移速率不完全已知的、具有匹配非线性和匹配外部扰动的马尔可夫跳变系统的奇异自适应积分滑模控制问题. 结合文章的仿真结果可见,所采用的控制方法具有合理性及有效性. 在这篇文章中,通过采用奇异自适应积分滑模控制策略研究了转移速率部分已知的、具有匹配非线性和匹配外部扰动的连续时间马尔可夫跳变系统随机容许性问题. 首先,构建了合适的积分型滑模面,再采用了模型转化方法,基于滑模动力学理论并结合滑模面得到了滑模动力学方程,并将其与原系统结合构造了所期望的奇异马尔可夫跳变系统;然后在转移速率部分已知的情况下,以线性矩阵不等式的形式给出了能保证所得奇异马尔可夫跳变系统随机容许性的充分条件;在此基础上构造了自适应滑模控制器,所设计的控制器也保证了系统状态轨迹的可达性. 通过最后的仿真案例可以看出所提出方案的准确性及有效性.2 主要结果
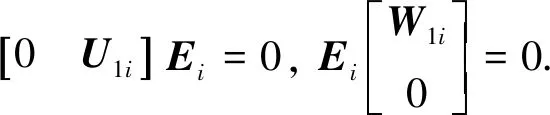



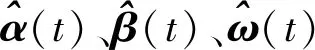

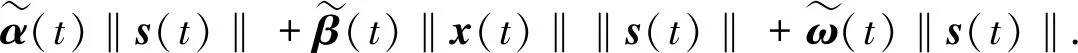

3 仿真算例
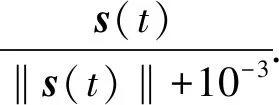

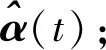


4 总 结
