具有饱和发生率的多斑块传染病模型的动力学分析

李宇航, 刘茂省②

(①中北大学数学学院,030051,山西省太原市;②北京建筑大学理学院,102616,北京市)

0 引 言

传染病一直是全球公共卫生面临的重大威胁,给人们的生活和健康造成了严重的危害. 近年来,随着旅行的便捷和全球化的发展,人们在世界各地之间的交往变得更加频繁. 然而,人口流动的增加极大地加快了不同地区之间传染病传播的速度. 例如2002年爆发的严重急性呼吸综合征(SARS)在6个月的时间内便传播到全球28个国家[1]. 2019年的新冠肺炎在世界各地迅速传播,仅用了4个月时间就扩散到了200多个国家和地区[2]. 人类在全球范围内的频繁移动导致了不同国家和地区之间传染病传播的风险显著增加. 因此,人口流动影响了传染病的传播动力行为,对疾病的流行具有重要影响.

为了研究人口流动如何影响传染病的传播,许多学者对斑块传染病模型进行了分析[3-5]. 文献[6]考虑了一个种群在多个地区间迁移的模型,研究了地区之间的个人旅行对SARS全球传播的影响. 文献[7]建立了一个斑块环境中具有疫苗接种的SIR模型,同时考虑了人口流动性增加和疫苗接种对传染病传播的影响. 文献[8]考虑了人口在p个斑块间迁移的SEIRS模型,得到了疾病持续和消亡的阈值,并分析了平衡点的稳定性. 文献[9]建立了一个广义的SEIR多斑块模型,讨论了人口迁移对COVID-19传播的影响. 文献[10]建立了一个具有出入境检查的SEIR斑块模型,研究了多种筛查策略对控制甲型H1N1流感的作用. 文献[11]利用多斑块新冠病毒斑块模型来研究疾病的地域扩散,并探讨了控制疾病在斑块间扩散的措施.

疫苗接种和隔离是预防和控制传染病传播的两种有效且常用的措施,被广泛运用于各种传染病的防治[12]. 疫苗接种能够使人体产生免疫力,隔离能够阻断传染病在人群中的传播. 因此,研究具有接种和隔离的传染病模型是很有必要的. 基于以上考虑,本文综合疫苗接种、隔离和人口迁移对传染病传播动力学的影响,建立了一个结合接种和隔离的多斑块传染病模型.

1 模型建立

将每个斑块的人群划分为6个仓室:易感者类Si(t),接种者类Vi(t),潜伏者类Ei(t),感染者类Ii(t),隔离者类Qi(t)和恢复者类Ri(t). 假设隔离者不能在斑块间流动,其他子群体能够在任意两个斑块间流动. 于是,建立如下具有饱和发生率的n斑块SVEIQR传染病模型:

(1)

其中Λi为第i个斑块中新生儿的数量,i=1,2,…,n;pi为第i个斑块中新生儿的接种率;βi为第i个斑块中疾病的传播率;μi、di分别为第i个斑块中的自然死亡率和因病死亡率;由于疫苗不是百分之百有效的,接种者仍然可能被感染,因此,用ki表示第i个斑块中的疫苗失效率;σi为第i个斑块中潜伏者到感染者的转移率;qi、γi分别为第i个斑块中感染者的隔离率和隔离者的恢复率;aij、bij、cij、dij、eij分别为第j个斑块中的易感者、接种者、潜伏者、感染者和恢复者到第i个斑块的迁移率. 以上所有参数都为正常数.

2 基本再生数和平衡点的存在性

考虑无病状态Ei=Ii=Qi=0, 则系统(1)的无病平衡点满足如下的方程组

(2)

将系统(2)转化为矩阵的形式

(3)

其中

S=(S1,S2,…,Sn)T,V=(V1,V2,…,Vn)T,R=(R1,R2,…,Rn)T,P=diag(p1,p2,…,pn),

Λ=(Λ1,Λ2,…,Λn)T,0=(0,0,…,0)T,

由于H1、H2、H3均为对角占优矩阵,并且所有非对角线元素都为负数. 因此,根据文献[13]第6章可知,H1、H2、H3均为非奇异的M矩阵,且矩阵的逆均为正. 从而,线性系统(2)存在唯一的正解

综上,系统(1)存在唯一的无病平衡点E0=((S0)T,(V0)T,0T,0T,0T,0T).

由Kuniya[14],可求得系统(1)的正不变集为

其中

(S,V,E,I,Q,R)=(S1,V1,E1,I1,Q1,R1,…,Sn,Vn,En,In,Qn,Rn).

接下来计算系统(1)的基本再生数R0. 利用下一代矩阵法[15],可得

其中

V32=diag(-q1,…,-qn),V33=diag(μ1+γ1,…,μn+γn),

3 无病平衡点的稳定性

定理1当R0<1时,无病平衡点E0在Γ内是局部渐近稳定的;当R0>1时,E0不稳定.

证明系统(1)在E0处的线性化方程写作矩阵形式为

(4)

其中X=(E1,E2,…,En,I1,I2,…,In,Q1,Q2,…,Qn)T.

因为矩阵F为非负矩阵,矩阵V为非奇异矩阵,由文献[16]的定理2可知s(F-V)<0(>0)当且仅当R0<1(>1),其中s(·)表示矩阵·特征值实部的最大值. 所以当R0<1时,矩阵F-V所有特征值的实部均为负数,因此E0是局部渐近稳定的. 当R0>1时,矩阵F-V至少存在一个特征值具有正实部,因此E0是不稳定的.

定理2 当R0<1时,无病平衡点E0在Γ内是全局渐近稳定的.

证明因为V-1F=V-1FV-1V,所以V-1F与FV-1相似,则ρ(V-1F)=ρ(FV-1)=R0. 通过Perron-Frobenious定理[17],非负不可约矩阵V-1F存在正的左特征向量(l1,l2,…,l3n)对应于特征值ρ(V-1F),即

(l1,l2,…,l3n)V-1F=(l1,l2,…,l3n)R0.

考虑Lyapnuov函数

(5)

其中(u1,…,un,v1,…,vn,w1,…,wn)=(l1,l2…,l3n)V-1.对L沿着系统(1)的解求导,可得

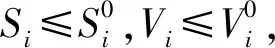
=(u1,…,un)(F1I-V11E1)-(v1,…,vn)(V21E+V22I)-(w1,…,wn)(V32I+V33Q)

=(u1,…,un,v1,…,vn,w1,…,wn)(F-V)X=(l1,l2…,l3n)V-1(F-V)X

=(l1,l2…,l3n)(V-1F-E)X=(l1,l2…,l3n)(R0-1)X≤0,

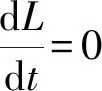
4 数值模拟和敏感性分析

对于系统(1),通过数值模拟来验证理论结果. 以2个斑块为例,并选取初始值为:(S1(0),V1(0),E1(0),I1(0),Q1(0),R1(0),S2(0),V2(0),E2(0),I2(0),Q2(0),R2(0))=(600,300,120,100,80,250,800,600,120,80,60,200). 假设aij=bij=cij=dij=eij=mij,其中i,j=1,2且i≠j.

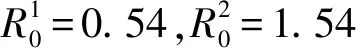
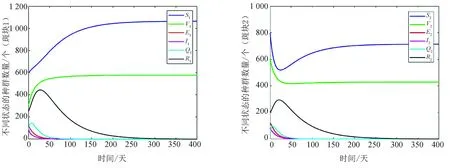
图1 各人群随时间的变化图(R0<1)

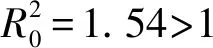
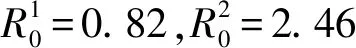
图2 各人群随时间的变化图(R0>1)

图3(下页):利用PRCCs(偏秩相关系数法)来分析R0对参数的敏感性. 由图3可知,p1、p2、q1、q2、μ1、μ2、m21与R0呈负相关,其中q1、q2相关性最强,β1、β2、σ1、σ2、m12与R0呈正相关,其中β1、β2相关性最强. 结果表明,增大每个斑块的疫苗接种率p1、p2和隔离率q1、q2都能使基本再生数R0减小,从而控制传染病的传播. 此外,迁移率m12的增加能使R0增大. 因此,人口从高风险地区(R0>1)到低风险地区(R0<1)迁移的增加将会加快两斑块间传染病的传播.

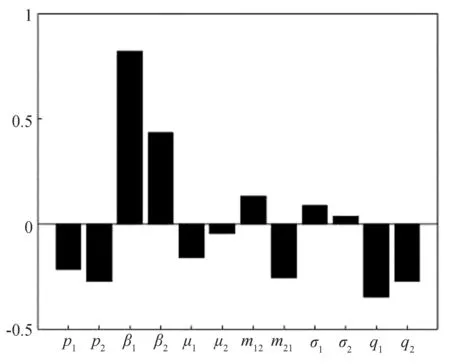
图3 R0与参数的相关性

5 结 论

本文建立了一类具有饱和发生率的多斑块SVEIQR模型,并探讨了无病平衡点的存在性和稳定性. 根据数值模拟和敏感性分析,我们得到了如下结论:

(1)对于两斑块模型,当疾病在斑块1中灭绝,而在斑块2中持续时,如果斑块2的基本再生数较小,可能导致疾病在两个斑块中灭绝. 如果斑块2的基本再生数较大,可能导致疾病在两个斑块中传播. 因此,人口迁移既可能抑制疾病在高风险地区的传播,也可能促进疾病在低风险地区的传播.

(2)提高疫苗接种率和增加隔离率都能够减少基本再生数的大小,从而控制疾病的传播. 此外,人口从高风险地区到低风险地区迁移的增加将会增大基本再生数的值,从而促进传染病的传播. 所以,当疾病爆发后,我们应该及时进行疫苗接种并采取隔离措施. 同时,应严格控制高风险地区的人口向外流动,这有助于减少疾病在斑块间的扩散.