带有扰动的适型分数阶时滞系统的稳定分析

高 扬

(大庆师范学院数学科学学院,163712,黑龙江省大庆市)

0 引 言

自从Khalil R定义了适型分数阶导数[1],一些学者已经着手研究适型分数阶系统的稳定与镇定问题[1-6]. 比如,文献[4]通过使用Lyapunov函数研究适型分数阶非线性系统的稳定与渐近稳定性. 实际应用的系统经常被扰动、误差、时滞等综合因素所影响. 这就要求系统不但具有稳定性质,同样具有抗干扰性质.

在捕捞管理的背景下,Collie 和 Spencer[7]引入了一种阈值策略(TP),它介于众所周知的常数逃逸策略和常数收获率策略之间. TP 的定义如下:如果估计的物种密度低于先前选定的阈值水平,则收获停止; 超过阈值,则进行收获. TP 被使用在诸如陆地收获、放牧和控制水生植被等多个领域[7-14].

纵观近年来的研究成果,基于TP策略的适型分数阶系统还没有被研究. 这主要是基于适型分数阶系统,特别是适型分数阶时滞系统的Filippov系统理论没有建立.

本文基于Lyapunov理论,综合考虑时滞和扰动对适型分数阶系统的影响,建立全新的稳定与镇定定理.

1 主要结论

定义1[1］假设函数h定义于[a,+∞),函数h从a开始阶为α(α∈(0,1])的适型分数阶导数定义为

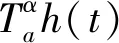
1.1 时滞适型分数阶系统稳定性分析

令C([a,b],)表示一个连续函数φ:[a,b]→构成的Banach空间. 令τ>0表示系统的最大时滞. 令Cτ=C([-τ,0],). 考虑带有扰动的适型分数阶系统

(1)

其中xt0为初始条件;T为适型分数阶导数算子,α∈(0,1);f:n×m→n为局部Lipschtiz的;x(t)∈n,v(t)∈E⊆m分别为式(1)在t∈+时刻的状态和扰动影响. 这里假定f(0,0)=0.

有如下定理成立.

定理1对系统(1)而言,若存在可微正定的Lyapunov-Krasovskii泛函V(xt)=V1(x(t))+V2(xt)和α1,α2,β1,β2∈K∞满足:

(1)α1(‖x‖)≤V1(x(t))≤α2(‖x‖);

(3)存在K函数σ1,和正数β,使得任意x∈n,任意v∈E⊆m,有

则系统式(1)渐近稳定的.

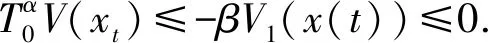
由单调性,知V1(x(t))+V2(xt)≤V1(x(t0))+V2(xt0). 对任意ε>0,由条件(1)有

由条件(2)有

α1(‖x(t)‖)≤V1(x(t))≤V1(x(t))+V2(xt)≤V1(x(t0))+V2(xt0).

进而

成立. 稳定性证毕. 下面给出渐近稳定性的证明.

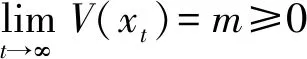
以下只需说明m=0即可. 可以反证,若m>0,则存在γ>0,T>0,对任意t≥T有‖x(t)‖≥γ.

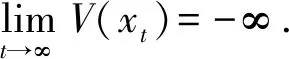
上述定理只是实现了适型分数阶时滞系统的渐近稳定性,此稳定性依赖于初始时刻t0. 由于一致渐近稳定性,在时滞系统应用广泛. 因此,有必要在渐近稳定基础上,研究系统的一致渐近稳定性.

考虑带有扰动的适型分数阶系统

(2)

式(2)中系统的条件要求,与系统(1)相同. 有如下定理成立.

定理2对系统(2)而言,若存在可微正定的Lyapunov-Krasovskii泛函V(xt)=V1(x(t))+V2(xt)

和α1,α2,β1,β2∈K∞满足

(1)α1(‖x‖)≤V1(x(t))≤α2(‖x‖);

(3)存在K函数σ1和正数β,使得任意x∈n,任意v∈E⊆m,有

则系统式(2)一致渐近稳定的.

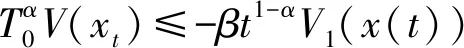
类似于定理1有

这表明δ与t0选取无关,故关于t具有一致性. 证毕.

1.2 基于TP策略的适型分数阶时滞系统稳定性分析

以下考虑阈值管控策略,应用其到适型分数阶时滞系统中. 设非线性系统如下描述

(3)

f、g为局部Lipschtiz的. 这里不连续项出现在控制项u(t)=(u1,u2,…,un)中. 采取阈值(TP)管控策略. 即

而取u2(t)=u3(t)=…=un(t)=0. 这意味着仅对第一个分量实施TP控制.

注1一般地,多个平衡点中,有的是稳定,有的不稳定.

假设系统(3)的所有的Filippov解在[t0-τ,+∞)上存在. 事实上,由微分包含的上半连续性,解的存在性得到保证.

首先,给出本文需要的Filippov解概念.

定义2一个绝对连续函数x:[t0-τ,a]→q称为系统(1)的定义于区间[-τ,a]上的关于初始条件xt0=x0的Filippov解,若x(t)满足

定理3对系统(3)而言,若存在可微正定的Lyapunov-Krasovskii泛函V(xt)=V1(x(t))+V2(xt)和α1,α2,β1,β2∈K∞满足:

(1)α1(‖x‖)≤V1(x(t))≤α2(‖x‖);

(3)存在K函数σ1和正数β,使得任意x⊆n,任意v∈E⊆m,有

V3(x(t))-V3(x(t-τ))≤-βV1(x(t));

则系统式(3)渐近稳定的.

证明首先,取过xt0的Filippov解x(t),则x(t)绝对连续而V1(x(t))为局部Lipschtiz,有V1(x(t))几乎处处可微. 由可测选择定理[13],存在γ(t)∈I(x(t)),且由条件(2)有

≤-βV1(x(t))≤0, a.e.t≥0.

进而有V(xt)单调递减有下界(下界为0). 以下证明同定理1类似. 综上,证毕.

为了实现不连续时滞系统的一致渐近稳定,考虑如下系统

(4)

式(4)中系统的条件要求,与系统(3)相同.

有如下定理成立.

定理4对系统(4)而言,若存在可微正定的Lyapunov-Krasovskii泛函V(xt)=V1(x(t))+V2(xt)和α1,α2,β1,β2∈K∞满足

(1)α1(‖x‖)≤V1(x(t))≤α2(‖x‖);

(3)存在K函数σ1,和正数β,使得任意x⊆n,任意v∈E⊆m,有

t1-αV3(x(t))-t1-αV3(x(t-τ))≤-βt1-αV1(x(t));

则系统式(4)一致渐近稳定的.

2 例 子

考虑如下适型分数阶系统

(4)

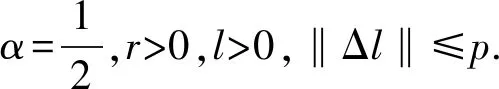
取Lyapunov泛函为

由可测选择定理,存在ξ(t)∈I(x(t)),经计算有

(l+p)[x2(t)-x2(t-τ)]≤-2rx2(t)+2(l+p)x2(t)+2x2(t)≤-βx2(t)

几乎处处成立. 这里β=2(r-l-p-1),故系统的零解是渐近稳定的.

3 结 论

本文基于非线性系统Lyapunov稳定理论,在适型分数阶导数意义下,针对带有扰动的分数阶时滞非线性系统,研究其稳定与镇定. 首先,基于Lyapunov-Krasovskii泛函思想,给出带有扰动的适型分数阶时滞系统稳定定理. 其次,基于TP管控策略,在Filippov解的意义下,给出带有扰动的时滞适型分数阶系统反馈镇定定理. 下一步,将深入研究适型分数阶生态系统的控制问题,建立镇定定理.