基于PRP共轭梯度的图像去噪算法

2024-01-26孙肖丽田茂英

曲阜师范大学学报(自然科学版) 2024年1期

孙敏, 孙肖丽, 田茂英

(①枣庄学院数学与统计学院;②山东煤炭卫生学校, 277160,山东省枣庄市)

0 引言

通过视觉感知图像是人类认识与了解现实世界的重要手段. 数字图像利用一个数字序列表示图像,便于使用计算机对其进行各种图像处理. 在数字化采样及传输过程中, 数字图像容易受到各种噪声的污染,降低了图像的可读性. 在追求高品质视觉体验的时代,数字图像的降噪处理引起了业界的广泛关注,该问题已成为数字图像领域的一个重要研究课题. 目前学术界提出了多种降低噪声的方法,包括利用线性拉普拉斯滤波器的模糊图像处理;利用二维中值滤波器的椒盐噪声图像处理[1];利用一阶原始-对偶方法的运动模糊图像处理[2];利用共轭梯度法的模糊图像处理[3];利用两阶段法的椒盐噪声图像处理[4];利用交替方向法处理含噪声及缺失像素的视频背景与前景分离问题[5]等.

数值实验表明,即使椒盐噪声浓度达到90%,两阶段法也能得到比较高的峰值信噪比(PSNR/dB),这说明该方法修复的图像比较好地还原了原始图像. 在第一阶段该方法利用自适应中值滤波器(AMF)找出受椒盐噪声污染的像素坐标. 在第二阶段该方法通过求解一个无约束最优化问题填补椒盐噪声处的像素值. 通过先检测再填充的方式,该方法有效地提高了数字图像去噪处理的速度与质量.

由上面的分析可以看出,两阶段法的关键在于第二阶段的无约束最优化问题的求解. 共轭梯度法是求解无约束最优化问题的最优秀的算法之一. 众多的共轭梯度法中,PRP共轭梯度法又是数值表现最好的共轭梯度法之一. PRP共轭梯度法在理论上存在的一个缺点是其收敛性条件比较苛刻. 对于一般的目标函数,即使采用精确线搜索,其也可能发散[6]. 本文设计了一类PRP共轭梯度法,该方法在较弱的条件下具有更强的全局收敛性,即其序列梯度趋于零,而不是通常共轭梯度法的序列梯度下极限趋于零. 同时将该方法应用到两阶段法的无约束最优化问题.

1 修正PRP共轭梯度法

考虑光滑无约束最优化问题

minf(x):x∈n,

(1)

其中f(x):n→是可微函数,其梯度记为∇f(x),简记为g(x),进一步g(xk)简记为gk. 由于计算量与存储量的优势,共轭梯度法是求解式(1)最有效的数值方法之一,尤其是求解大规模无约束最优化问题. 共轭梯度法属于一阶迭代算法,给定当前迭代点xk∈n,其迭代格式为

xk+1=xk+αkdk,k=0,1,2,…,

其中αk∈是步长因子,通常由非精确线搜索确定;dk∈n是搜索方向,由下式确定,

(2)

这里βk∈是区分不同共轭梯度法的参数,也就是说不同共轭梯度法的区别主要在于βk的不同表达式.βk经典的表达式包括

(3)

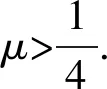
(4)

该方法继承了PRP共轭梯度法自动再启动的优点,即当迭代点前进量几乎为零时,该方法自动切换到最速下降法. 同时其还具有PRP共轭梯度法所不具备的优点,即充分下降性.

其次,为了得到收敛性分析中的一些关键不等式,修正PRP共轭梯度法采用如下Armijo型线搜索:步长αk是集合{υk,υkρ,υkρ2,…}中满足下面不等式的最大的α[7]:

f(xk+αdk)≤f(xk)-σα2‖dk‖4,

(5)

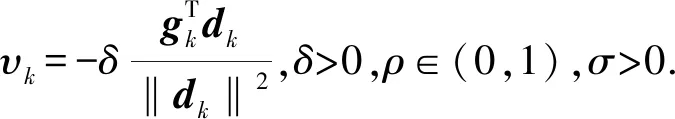
最后给出修正PRP共轭梯度法的算法流程.

步1 如果‖gk‖=0,停止,否则转步2.

步2 由Armijo线搜索式(5)确定步长αk.

步3 由式(4)确定搜索方向dk.

步4 令xk+1:=xk+αkdk,计算gk+1.

步5 令k:=k+1,返回步1.

2 修正PRP共轭梯度法收敛性分析

为了分析修正PRP共轭梯度法的收敛性,需要对式(1)施加如下假设:

(H1) 水平集Ω={x∈n|f(x)≤f(x0)}有界;

(H2) 在Ω的某个邻域中,梯度g(x)是Lipschitz连续的,即存在一个常数L>0,使得

‖g(x)-g(y)‖≤L‖x-y‖,∀x,y∈n.

(6)

下面的引理说明由式(5)生成的方向满足充分下降性.

引理2.1对于任意的k=0,1,2,…,由式(5)定义的搜索方向dk满足

(7)

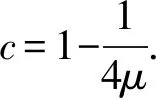
其中最后一个不等式使用了柯西-施瓦兹不等式. 证毕.

再由柯西-施瓦兹不等式与式(7)得

c‖gk‖≤‖dk‖,k=0,1,2,…,

(8)

由此得

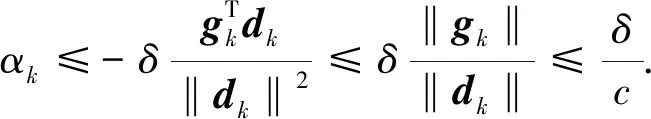
(9)

下面分析如果xk不是问题(1)的稳定点,则Armijo型线搜索式(5)会在有限步内终止.

引理2.2当‖gk‖≠0时,Armijo型线搜索式(5)会在有限步内终止.

证明利用反证法. 假设结论不成立,则对任意正整数j,有

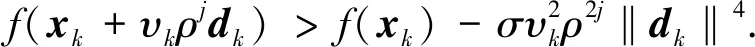
引理2.3假设(H1)与(H2)成立,则由式(5)确定的步长αk满足

(10)

下面的定理表明修正PRP共轭梯度法具有全局收敛性.

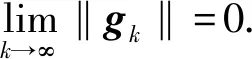
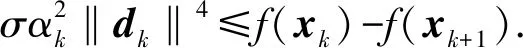
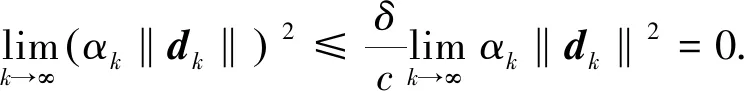
(11)

因此再结合式(8)得

(12)

下面利用反证法证明结论成立. 假设结论不成立,则存在常数ε0>0及无穷集合K⊆N,使得对于任意的k∈K,都有

‖gk-1‖≥ε0.

(13)

‖gk‖≥ε1.

(14)

于是结合式(12)得

(15)

另一方面,由搜索方向的定义式(4)得

(16)

由式(12)得,存在r>0,使得任意的k∈K,有αk‖gk‖≤r.将此式代入式(16)得

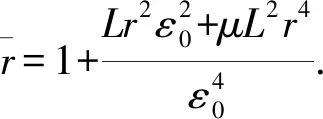
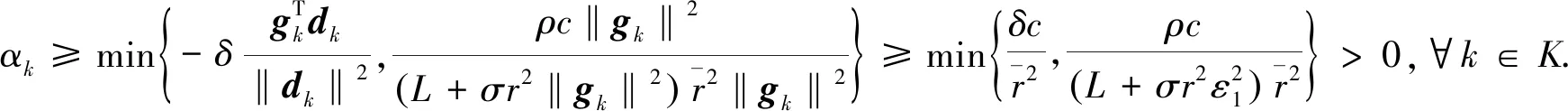
显然上式与式(15)是矛盾的. 这说明假设不成立. 证毕.

3 数值实验

下面将本文设计的PRP共轭梯度法(记为NPRPCG)应用到两阶段图像处理模型中,并与FR共轭梯度法(记为FRCG)以及文献[11]中的PRP共轭梯度法(记为CPRPCG)进行数值对比.

首先简单回顾一下两阶段法[4]. 令X=[xi,j]m×n表示一个数字图像,共m×n个像素.对于每个(i,j)∈A={1,2,…,m}×{1,2,…,n},令Vi,j表示(i,j)的4个最相邻点构成的集合,即

Vi,j={(i,j-1),(i,j+1),(i-1,j),(i+1,j)}.

对于点(i,j),令yi,j表示该点的正是像素值xi,j经过椒盐噪声污染后的观测值. 在第一阶段,两阶段法利用自适应中值滤波器检测椒盐噪声的位置. 令N⊆A表示检测到的可能含有椒盐噪声的像素点构成的集合;第二阶段,两阶段法通过求解下面的最优化问题填充椒盐噪声点处的像素值:

其中α是正则化参数,φα是保边函数,u=[ui,j](i,j)∈N是一个列向量(按字典序排列). 本实验中φα定义为Huber函数[11]:

其中α=10. 使用峰值信噪比(Peak signal-to-noise ratio,PSNR)来衡量图像修复的质量,

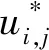
选取初始迭代点x0取为图像观测值. 本次实验采用如下测试图片Lena(256×256)、Cameraman(256×256)、Barbara(512×512)与Boat(512×512),见图1.

图1 原图片Lena、Cameraman、Barbara与Boat

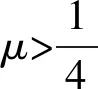
μ∈{0.25,0.35,0.45,…,2.05}.

图2 参数μ的灵敏度分析

由图2可以看出,PSNR对于μ的变化不是很敏感,而CPU对参数μ的变化比较敏感. 就PSNR来说,当μ=0.95时,NPRPCG的数值表现最好;就CPU来说,当μ=1.85时NPRPCG的数值表现最好. 因为CPU都在3 s左右,耗时比较小,且其大小与硬件的性能有很大关系,因此这个实验中以PSNR为参数的设定标准. 在下面的实验中取μ=0.95.

为了使得数值结果具有可比较性,3种算法都采用上面的运行策略. 当原图片受到不同椒盐噪声浓度r的污染时,表1给出了两种测试算法在算法终止时的PSNR、所需CPU(CPU,单位:s).

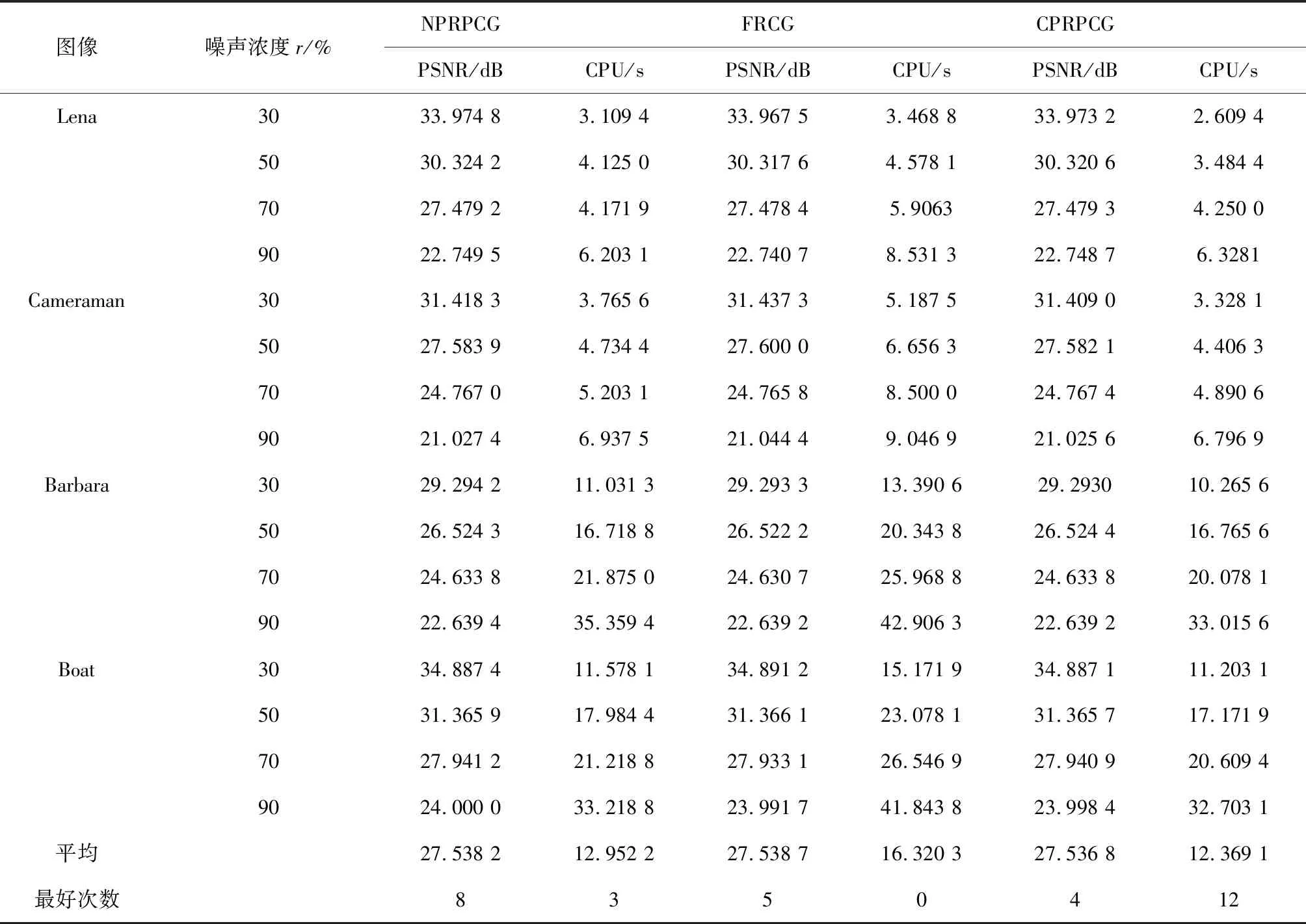
表1 不同噪声浓度下NPRPCG、CG_Descent与CPRPCG的数值对比

由表1可以看出,3类测试算法比较好地去除了椒盐噪声,即使其浓度达到90%,得到的PSNR也在20 dB以上. 这进一步验证了两阶段法的有效性,也说明了3种方法能够较好地处理两阶段法中的无约束最优化问题. 3类测试算法的区别只是共轭参数有细微的区别,这说明三者每次迭代的计算时间几乎一样,因此表1中没有给出迭代次数. 就平均CPU来说,CPRPCG的表现最好,FRCG表现最差,运行时间明显大于另外2个算法,多了3 s以上,而另外2个算法的平均CPU比较接近,相差0.583 0 s. 就平均PSNR来说,FRCG的表现最好,CPRPCG表现最差. 具体分析FRCG的PSNR指标可以看出,当Cameraman的噪声浓度为90%时,其PSNR明显比另外2个方法的PSNR高. 如果不考虑这一行,则3个算法的平均PSNR分别为27.972 2、27.971 7、27.970 9. 由此可以看出仅仅去掉了一组测试数据,FRCG在PSNR方面的优势就没有了. 这与FR共轭梯度法具有好的理论结果但数值表现较差的结论是一致的. 同时,表1中加粗的数据表示其是该组测试中表现最好的一个. 由表1的最后一行可以看出,就PSNR这个关键指标来看,NPRPCG取得最好的次数是最多的. 因此从数值表现上来说,NPRPCG优于FRCG与CPRPCG.

图3给出了在椒盐噪声浓度为70%时,NPRPCG、FRCG与CPRPCG的去噪效果.