利用求导法计算多连杆端点运动的加速度

陈鸿翔 沈 卫

(浙江省湖州市菱湖中学,浙江 湖州 313018)

1 问题呈现

如图1所示,长均为l的两杆用铰链P相连,两杆夹角为2α,其中一根杆的一端O固定不动,另一根杆的自由端Q以大小和方向恒定的速度v0开始运动,v0平行于两杆夹角的角平分线。求Q端开始运动后经过非常短的时间,连接两杆的铰链P的加速度。

图1

笔者在与学生共同探讨这道两连杆问题中端点运动的加速度求解问题,分别运用了参考系变换下运动的对称性和求导两种方法,却得到了两个完全不同的结果。是其中一种方法中不适用于该问题的解决,还是运用过程中忽略了某些细节导致结果出现差异?

2 解答方法及其分析

2.1 运用基于对称性的加速度矢量合成法

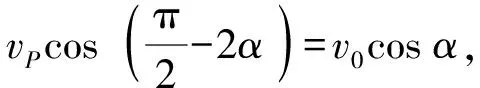
图2

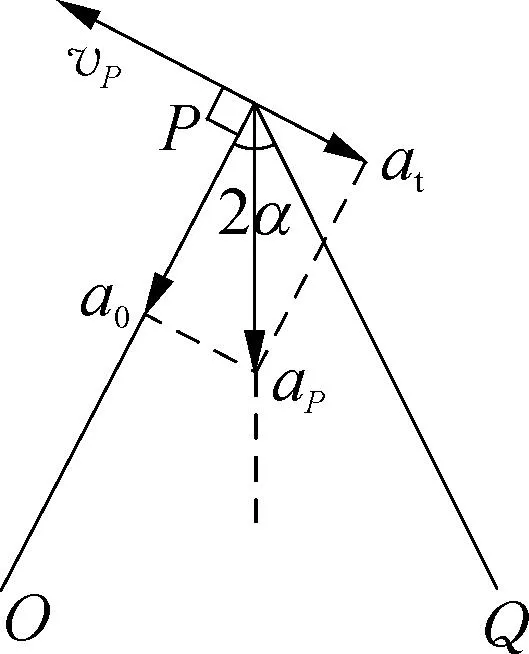
图3

2.2 运用求导法求解P点的切向加速度

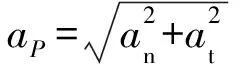
2.3 连杆运动经过极短时间后P点绕O点运动的速度求解

考虑到问题是求解经过非常短的时间后P点的加速度,不妨考虑当经过极短时间后P点速度的表达形式,故画出连杆OPQ经Δt(Δt趋于0)转动到OP′Q′的示意图(图4)。

图4

点评：由于该题只考虑运动开始后很短的一段时间内P的加速度,因此根据几何近似关系,可充分利用OP杆与PQ杆夹角不变这一几何特征,求解P点的速度关系式,进而对该关系式中的变量α′在零时刻的取值求时间的导数,获取加速度的定量关系。虽然该方法略为繁琐,且需要学生具备一定的数学能力,但是更具有普适性。一旦问题中不再具有对称性,显然就难以运用2.1中的解法,但是运用导数,依旧可以实现对连杆端点加速度的定量分析。

3 对三连杆端点加速度的求解

利用求导法不仅可以定量分析两连杆端点运动的加速度,对于存在两个动点的三连杆问题也能够探讨其端点的加速度关系。

例：图5所示为用刚性细杆AB、BC、CD连成的平面连杆结构。AB和CD可分别绕过A、D的垂直于纸面的固定轴转动,A、D两点位于同一水平线上,BC杆的两端分别与AB杆和CD杆相连,在B、C处均有一铰链。当AB杆绕A轴以恒定的角速度ω转到图5所示位置时,AB杆处于竖直位置。BC杆与CD杆都与水平方向成角45°,已知AB杆的长度为l,BC杆和CD杆的长度由图5给定,求此时C点的加速度(用与CD杆之间的夹角表示)。

图5

解析：B、C为动点,在图5所示时刻,B点的速度、C的速度及B相对于C的速度分别为：vB=lω,vC=lωcos 45°,vBC=lωsin 45°。

图6

点评：利用求导法解决连杆加速度问题,其关键在于确定连杆运动的几何特征,能够在连杆运动较短时间的过程中确定角度变化的关系,并能够运用速度投影法确定不同端点之间速度的关系,从而根据已知的速度推导未知速度的表达式,对速度表达式求关于时间的导数,实现对端点切向加速度的求解。

4 结语

连杆端点运动加速度的计算作为高中物理中的复杂问题之一,一般都有多样的解法,一些解法在数学运算、物理建模上对学生有较高要求。笔者认为,直观形象的解法契合学生的认知方式,运用求导法解决物理问题在数学上的要求虽然较高,但是在突出结论的直观与形象、反映问题的物理本质方面显然更具优势。如果能从最直观的物理概念与模型出发,展现问题本身所包含的物理思想与内涵,相信会对学生提高学习物理的兴趣起到一定的促进作用,会促进学生拓宽解题视野、提升核心素养。