立式轴流泵装置叶轮间隙泄漏流动与受力稳定性研究

龚 严

(安徽省水利水电勘测设计研究总院有限公司，安徽 合肥 230088)

1 概述

轴流泵具有大流量、低扬程、高效率等特点，广泛应用于农田灌溉、防洪排涝、城市给排水及跨流域调水等工程[1-2]。在轴流泵实际运行过程中，为了使叶片角度可调节，叶轮叶片与对应外壁之间会存在一定间隙，即叶顶间隙[3]。间隙泄漏流动是轴流泵运行过程中的典型特征，具有流速高和流动紊乱的特点，其与叶道主流、壁面边界层和叶片尾流的相互作用，形成泵叶轮内复杂的漩涡结构[4]。间隙泄漏流不仅会导致流量损失，降低轴流泵的运行效率，而且会引发泄漏涡，进而堵塞流道，诱导水力振荡，影响泵的稳定运行[5]。因此，研究不同间隙尺寸和不同流量对轴流泵叶顶间隙流动与受力稳定性的影响，具有一定的工程意义。

针对轴流泵叶顶间隙的研究，当前学者主要通过模型试验和数值模拟两种手段来研究泵内间隙泄漏流动特征。Wu等[6-7]采用PIV技术对轴流泵叶顶间隙流动和叶顶泄漏涡的发展过程进行了试验研究，阐述了叶顶泄漏涡的发生、发展及溃灭过程。张德胜等[8-9]分析了轴流泵叶顶泄漏涡的结构及其产生过程，并对叶顶间隙区域的空化流动和压力脉动进行了数值模拟。Shen等[10]选用不同叶顶间隙的轴流泵方案进行了全流场数值模拟，结果表明叶顶泄漏涡的流动结构及其输运与叶顶间隙宽度密切相关。孙壮壮等[11]研究了不同流量工况下轴流泵叶轮径向力分布情况，结果表明不同流量工况下径向力呈现一定的周期性分布，小流量工况下径向力分布最不稳定。Hao等[12-13]研究了叶顶间隙对称和非对称两种情况下混流泵的径向力特性变化情况，研究结果表明叶顶间隙泄漏流动会影响径向力的特性。目前，大部分研究主要是对不同间隙尺寸和不同工况分开进行研究[14]，叶轮受力特性的研究主要针对水泵水轮机和其他泵装置，对于轴流泵叶轮受力特性研究则较少，关于叶顶间隙对叶轮受力特性的影响研究也不够充分。

本文基于ANSYS Fluent平台对立式轴流泵进行三维数值模拟，选取具有代表性的3种间隙尺寸作为研究对象，在3种典型流量工况下分析研究泄漏流动对叶片表面压力分布的影响并对于轴流泵装置叶轮的受力特性进行分析。最后，总结间隙尺寸和流量工况对轴流泵装置叶轮受力稳定性的影响，以期为轴流泵的安全、稳定及高效运行提供参考。

2 计算模型与数值计算方法

2.1 几何模型

本文以某泵站立式轴流泵的原型装置为研究对象，其组成部分如图1所示，包括肘形进水流道段、叶轮段、导叶段及虹吸式出水流道段。原型泵的基本参数分别为叶轮直径D=1550mm，叶轮叶片数Z=4，转速n=125r/min，设计流量Q=30m3/s，设计扬程H=4.15m。叶顶间隙δ共设置了3种方案，分别为1.55、6.20、18.6mm，为使研究成果更具普适性，对叶顶间隙与叶轮半径的比值做无量纲化处理，间隙系数θ的计算如下：

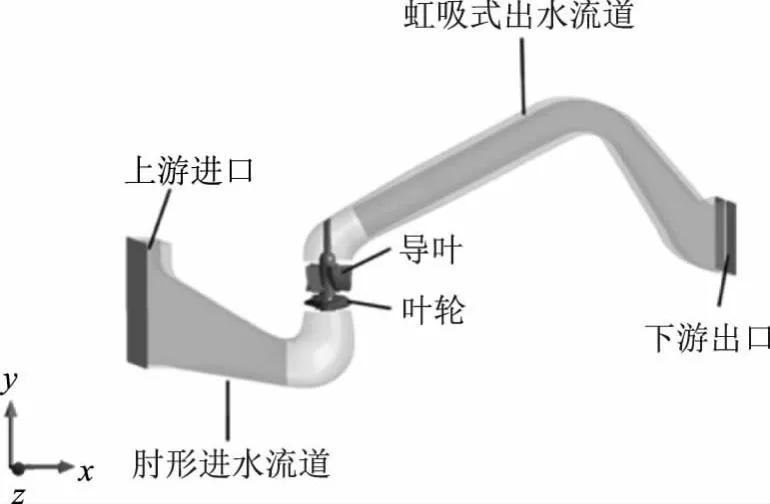
图1 立式轴流泵三维模型图

θ=δ/R

(1)

式中，δ—不同方案下间隙尺寸，mm；R—叶轮标称半径，mm。

本文选取具有代表性的3种间隙：小间隙(δ=1.55mm)、中间隙(δ=6.20mm)、大间隙(δ=18.60mm)，同时选取3种流量工况：小流量工况(0.8Q0)、设计工况(Q0)、大流量工况(1.2Q0)，对3种间隙尺寸在不同流量工况下的间隙流动特征进行分析研究。

对不同方案下间隙尺寸无量纲化后得到的间隙系数值见表1。

表1 网格离散误差估计

2.2 网格划分与收敛性验证

为了保证良好的计算精度与收敛性，整体计算域网格采用结构化网格的划分方式。为了捕捉叶片近壁面处的流态分析，对叶顶间隙处进行了网格加密处理。对于小间隙(θ=1‰)，在叶顶间隙处设置10层网格；对于中间隙(θ=4‰)，在叶顶间隙处设置40层网格；对于大间隙(θ=8‰)，在叶顶间隙处设置120层网格；以保证不同间隙尺寸下间隙处网格密度相同。图2为中间隙(θ=4‰)计算域网格示意图。

图2 计算域网格示意图

对于计算域网格，选取多组网格方案进行网格无关性验证。如图3所示，当网格数目多到一定的数量级以后(G>600万)，网格数对数值模拟结果没有明显影响。为进一步分析网格的收敛性，采用Richardson外推法[15-16]，对3种不同间隙尺寸方案网格划分进行网格收敛性验证。验证结果见表1，3种方案的网格收敛指数均小于3%，满足计算要求。最终进水流道、出水流道和导叶段网格数确定为106万、119万、163万，3种间隙尺寸下的叶轮段网格数控制在300万以上，总体网格数控制在700万到1300万之间。各方案下的叶片表面y+值小于50，且叶顶区域值y+小于10，满足SSTk-ω湍流模型对近壁区y+值的要求[17]。

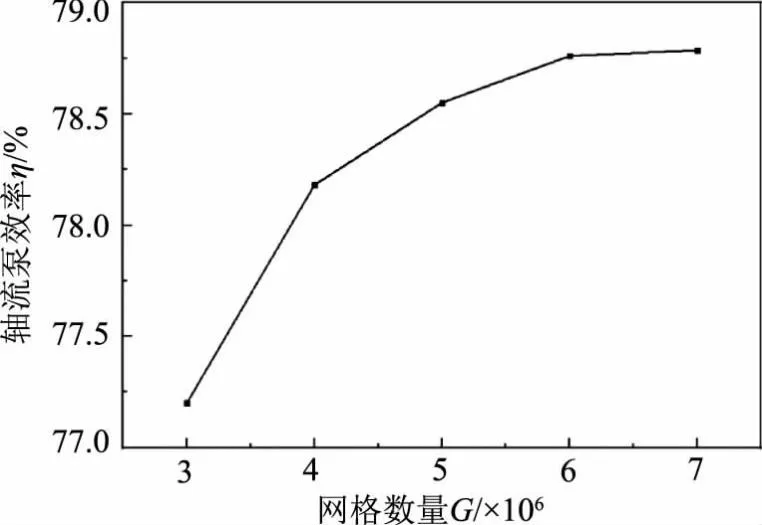
图3 不同网格数下的轴流泵装置效率

本文采用雷诺时均N-S方程与SSTk-ω湍流方程，对轴流泵内部流场进行数值模拟。进口边界条件设置为流量入口，出口边界条件设置为压力出口，叶轮域设置整体转动，叶轮外壳设置相反的转动速度，进口段轮毂不设置转动。除了进出口以及交界面以外的其他流体和固体接触面均设置为无滑移壁面，靠近壁面区域采用标准壁面函数进行处理。对于非定常计算，设置时间步长为设计转速下旋转周期的1/240，收敛精度为10-5。

2.3 模型试验验证

图4为轴流泵外特性测试试验装置，该试验在河海大学多功能水力机械试验台上进行。根据相似理论将轴流泵按照比例缩小至转轮直径为300mm的试验模型，模型泵的特征扬程与原型水泵保持一致，试验轴流泵装置叶轮段间隙系数θ=1‰。试验扬程测量通过安装段上下游布置型号为EJA110A(精度为±0.075%)的压力传感器测量，转速和扭矩采用湖南湘仪制造的JCZ-200N·m扭矩仪测量，精度均为±0.1%[17]。试验完成后，根据相似理论将模型试验成果换算成原型各参数值[18]。

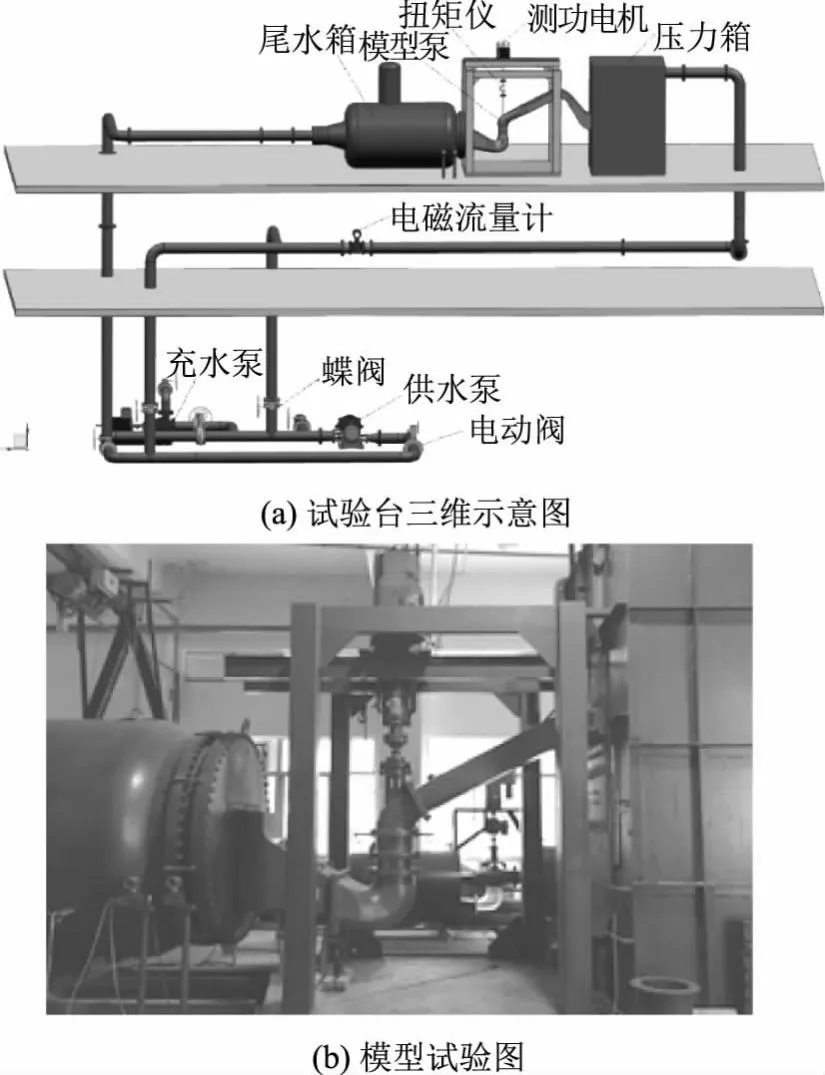
图4 轴流泵外特性测试试验装置图

为了验证数值计算模型的可靠性，对3种定间隙尺寸下5个典型工况(流量分别为0.8Q0、0.9Q0、1.0Q0、1.1Q0和1.2Q0)的泵内流动进行数值模拟计算，对水泵原型的扬程、效率进行了预测，并与试验结果进行了对比，如图5所示。θ=1‰时模型数值计算所得扬程、效率与试验结果吻合良好，但是效率曲线误差较高，这与试验误差较大有关。扬程和效率的模拟值与试验值最大相对误差分别为4.4%、4.1%，说明本文所采用的数值模拟方法可以比较准确地预测立式轴流泵外特性，因此轴流泵非定常流场的计算结果是可信的。由图5也可以看到，三种间隙的最优工况点都在设计流量，与试验结果一致，并且随着间隙的增大，扬程和效率值也会下降，且大流量工况下下降的幅度更大。

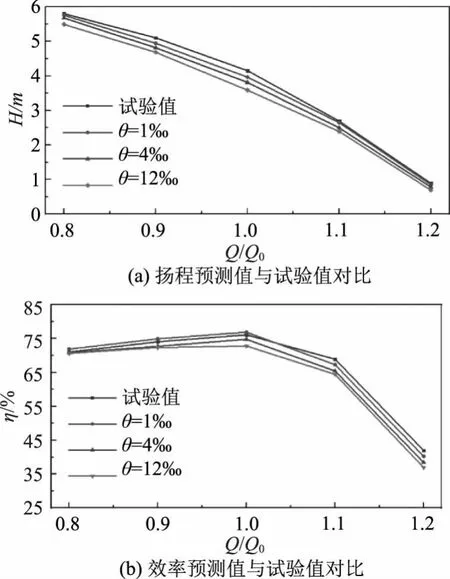
图5 立式轴流泵外特性预测值与试验值对比

3 结果与分析

3.1 叶顶泄漏涡涡核轨迹分布特征

为了分析不同工况下泄漏涡的形态特征，选用Q方法表征泄漏涡二维形态。图6为R*=0.98处截面轴向圆柱展开面的Q分布云图。其中R*=(R-Rh)/(Rc-Rh)，R为所取截面半径，Rh是轮毂半径(mm)，Rc是轮缘半径(mm)，叶片吸力面为SS，叶片压力面为PS。

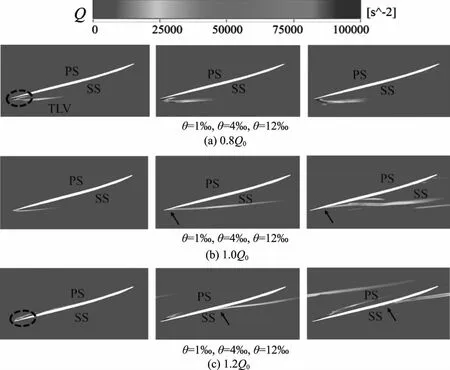
图6 R*=0.98处截面轴向圆柱展开面Q分布云图

从Q分布云图中可以看出，相同流量工况下，3种不同间隙尺寸下泄漏涡区域变化规律基本相同，在Q0和1.2Q0工况下(图6b和图6c)，随着间隙尺寸的增大，泄漏涡的初始位置的变化规律明显，在叶片吸力面处，从叶片前缘处逐渐向叶片尾缘处移动。相同间隙尺寸下，随着流量的增大，泄漏涡区域发生明显变化，0.8Q0工况下(图6a)泄漏涡集中在叶片前缘处，1.2Q0工况下在叶片压力面出现泄漏涡，并且随着间隙尺寸的增大，压力面的泄漏涡区域逐渐延长，但是θ=1‰时，大流量区域吸力面的泄漏涡不明显。

3.2 立式轴流泵装置叶片压力分布特性

为研究不同间隙和不同流量工况下，叶顶泄漏流动对轴流泵叶顶附近压力脉动特性的影响，定义压力系数Cp为：

(2)

式中，P—压力，Pa；Pin—叶轮段进口截面的平均压力，Pa；Vtip—叶轮叶片叶顶周向速度，m2/s。

为了进一步研究泄漏流动对叶片压力面和吸力面处压力特性的影响，图7展示了不同间隙尺寸下，R*=0.98处叶片截面的压力系数分布情况，弦长系数λ从0到1对应从叶片前缘到叶片尾缘的几何位置。由图7可知，不同间隙尺寸下，叶片压力面处的压力系数变化趋势基本一致，叶片吸力面处的压力系数随着叶顶间隙尺寸的增大发生明显变化，这说明在相同流量工况下，间隙尺寸主要对叶片吸力面处的压力分布产生影响，对叶片压力面的压力分布影响不大。由图7(b)可知，Q0工况下在叶片吸力面处，间隙尺寸的增加导致叶片吸力面处压力分布发生变化，当θ=12‰时，间隙尺寸的增大导致泄漏流增加，在叶片吸力面处出现局部低压区域的情况，特别是在λ=0.1附近，局部低压导致叶片表面压力曲线出现明显的下凹的趋势。由图7(a)和图7(c)可知，0.8Q0和1.2Q0工况下随着间隙尺寸的增大，叶片表面压差发生变化，特别是相比于其他两种间隙尺寸，θ=12‰处，叶片对水流的做功能力随着叶顶间隙的增大而下降，叶片表面压力差逐渐减小，这也是导致大间隙尺寸下扬程下降的重要原因。

图7 不同间隙尺寸叶片表面压力系数分布

图8展示了不同流量工况下，R*=0.98处叶片截面的压力系数分布情况。叶片表面压力差在不同的流量工况下存在明显差异，在叶轮的进出口区域，压差最大，随着流量的增大，叶片表面压力差最大值从叶片前缘处向叶片尾缘处移动。在叶轮进出口区域，由于水流的冲击作用导致叶片表面压力差较大，随着流量的增大，在叶片压力面叶片表面压力系数逐渐减小，在叶片的吸力面靠近叶片尾缘部分压力系数也逐渐减小。叶片吸力面和压力面之间的压力差反映了叶片的载荷特性，压力差越大，叶片表面所受荷载越大，叶片表面荷载特性随着压力差的变化而发生变化。由前文对不同流量工况下，叶顶泄漏涡涡核轨迹分布特征可以发现随着流量的逐渐增大，叶顶泄漏涡的初始位置也向叶片尾缘处移动，受到低压区域和泄漏涡的影响，叶片吸力面和压力面之间的压差发生变化，特别是在1.2Q0工况下，叶片表面压力差最大值移动幅度最大。压力差的变化导致叶片表面荷载主要集中区域由叶片前缘处向叶片尾缘处推移。在0.8Q0工况下，吸力面低压区域和叶顶泄漏涡主要集中在叶片前缘处，在λ=0.05附近，叶片进水边即叶片前缘处压力面出现高压区，导致此处压力面曲线出现上凸的趋势，叶片吸力面和压力面之间的压力差大于其他区域，叶片表面荷载主要集中于叶片前缘处。θ=12‰时(图8c)，在设计流量工况下，λ=0.2处吸力面压力系数曲线下凹，出现局部低压区域，叶片表面压力差增大，相比于0.8Q0工况，叶片表面荷载主要集中位置发生变化，向叶片尾缘移动。

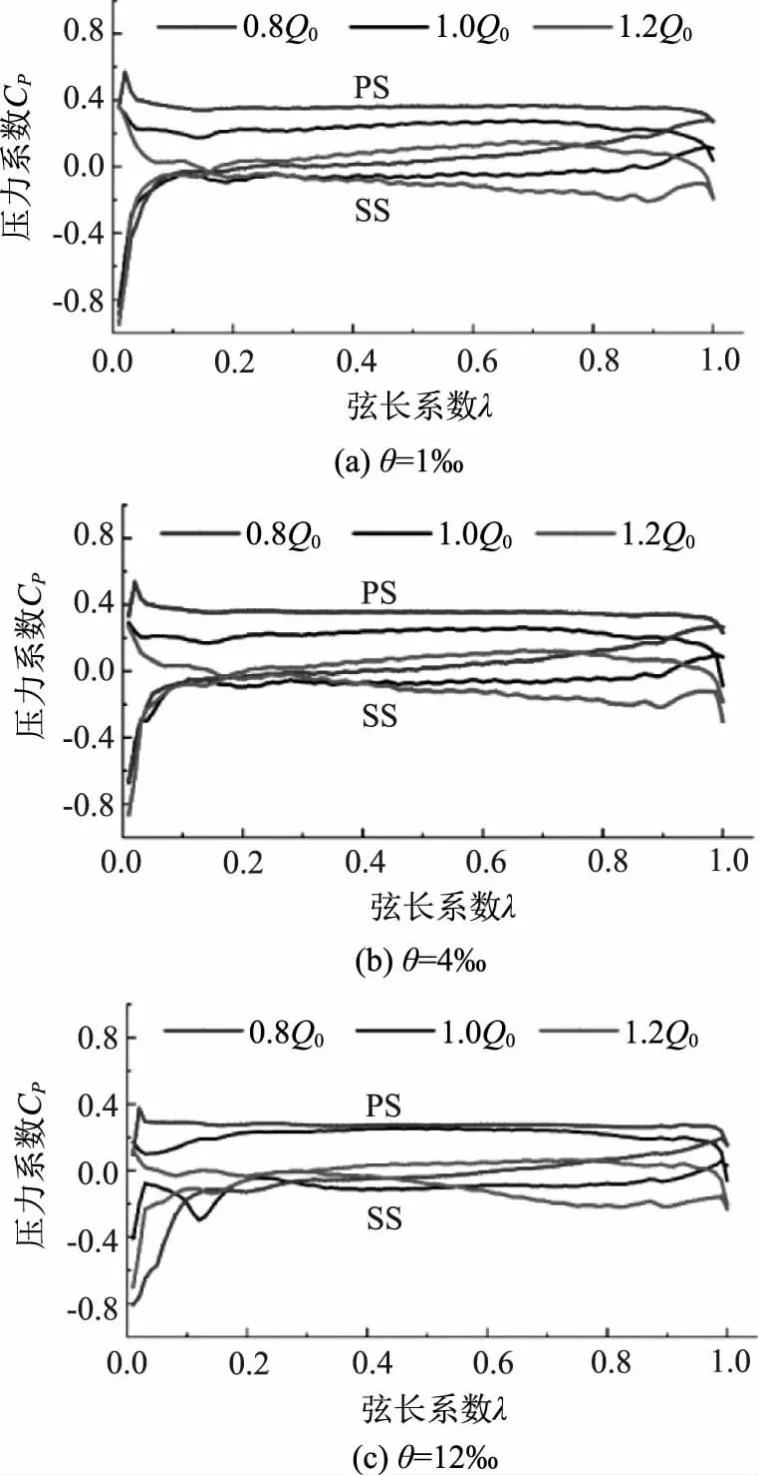
图8 不同流量工况叶片表面压力系数分布

3.3 立式轴流泵装置叶轮受力特性分析

轴流泵叶轮在高速旋转时，叶轮所承受的力主要为径向力，径向力的存在会使得转轴在交变应力作用下发生移动，从而偏移轴系方向，是导致转轴横向振动的重要原因，严重影响轴流泵的安全稳定运行。径向力是由于动静相互作用以及叶轮周围流场压力分布的不均匀性而引起的，在研究不同流动结构对叶轮径向受力的影响中，所计算的是整个转轮体的径向力。定义叶轮径向力计算如下：

(4)

式中，Fx—径向力在x方向的分力，N；Fz—径向力在z方向的分力，N。

图9为不同间隙尺寸下叶轮径向受力极坐标分布图。由图9可知，在0.8Q0工况下间隙尺寸对径向力曲线变化的影响明显，Q0和1.2Q0工况下间隙尺寸对径向力曲线变化的影响相对较小。0.8Q0工况下，叶顶间隙越大，径向力随时间变化规律的周期性越不明显，随着间隙尺寸的增加，叶顶泄漏流动更紊乱，泄漏流动产生较多的旋涡和回流，叶顶泄漏涡强度的增加诱导了压力场分布的显著变化，叶轮周围压力分布不均匀，这导致叶轮所受径向力随时间的变化不具有周期性，波峰和波谷之间波动幅度也逐渐增大。在设计流量和1.2Q0工况下，3种间隙尺寸下径向力随时间具有周期性变化规律，一个旋转周期内有4个波峰和波谷。1.2Q0工况下随着间隙尺寸的增大，叶轮受到的径向力先增大后减小，径向力波动幅度逐渐增大。与其它两种间隙尺寸相比较，θ=12‰时径向力虽然小于θ=1‰和θ=4‰时，但是径向力波峰和波谷之间的变化幅度大于θ=1‰和θ=4‰时，说明随着间隙的增大，叶轮所受径向力波动越大，轴流泵装置的运行稳定性受到影响。

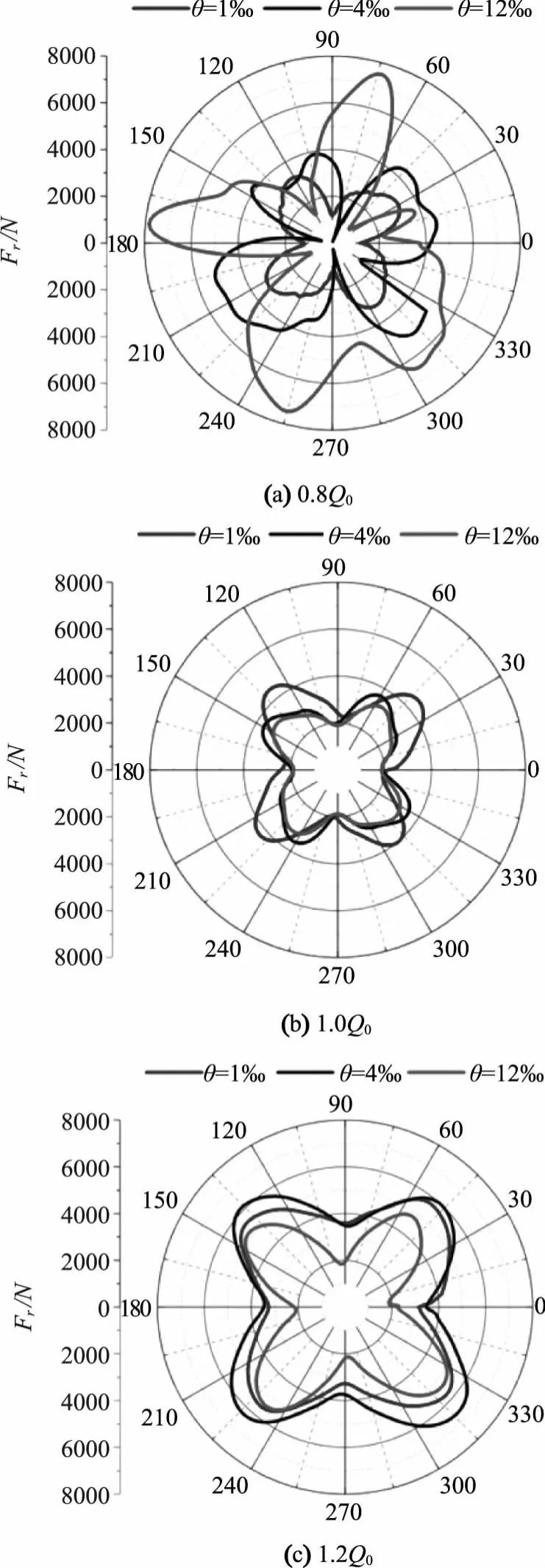
图9 不同间隙尺寸叶轮径向受力分布图

选取θ=1‰为例来研究一个空间旋转周期内，叶轮在0.8Q0、Q0和1.2Q0工况下所受的径向力，其中图10(a)为叶轮径向受力时域图，图10(b)为极坐标下的径向力分布图。由图10(a)可知在一个空间旋转周期内，不同流量工况下径向力随时间变化具有明显的周期性变化规律，每个旋转周期内的波峰和波谷与叶轮叶片数相对应。不同流量工况下径向力的幅值差异较大，且随着流量的增大而逐渐增大，1.2Q0工况下径向力幅值是设计流量工况和0.8Q0工况下的1.33和1.87倍。由极坐标图可知，在监测周期始末两时刻径向力轨迹基本闭合，说明此时受力已经稳定。不同流量工况下径向力轨迹相似，叶轮每旋转1/4圈，都会出现明显的波峰与波谷，这与10(a)的时域图中每个旋转周期内有4个波峰和波谷相对应。但是在0.8Q0工况下径向力曲线还存在一些不明显的次峰，说明0.8Q0工况下叶轮径向受力波动较大，容易引起轴流泵运行不稳定，对比图7—8可以发现，这一现象与小流量工况下叶轮进口处压力波动大有关。

图10 θ=1‰时不同流量工况叶轮径向受力分布图

4 结论

(1)叶顶泄漏涡的分布受间隙尺寸与流量工况的影响，相同流量工况下，随着叶顶间隙尺寸的增大，轴流泵叶顶泄漏涡在圆周方向延长；同一间隙尺寸下，随着流量的增大，轴流泵叶顶泄漏涡的初始位置逐渐向叶片尾缘处发展，并且在1.2Q0工况下叶片前缘压力面处出现泄漏涡。

(2)间隙尺寸对叶片压力面处的压力分布影响较小，对叶片吸力面处的压力分布影响较大，随着间隙尺寸的增大，叶片表面压力差逐渐减小。在不同流量工况下叶片表面压力分布存在明显差异，受到泄漏流动的影响，在0.8Q0工况下叶片前缘处压力面曲线出现上凸的趋势，叶片表面压力差最大值位于叶片前缘处，随着流量的增大，叶片表面压力差最大值从叶片前缘处逐渐向叶片尾缘处移动。

(3)在一个旋转周期内，Q0和1.2Q0工况下径向力随时间具有周期性变化规律，在每个旋转周期，叶轮受力受动静干涉作用的影响，波峰和波谷数与叶轮叶片数相同。Q0工况下间隙尺寸对叶轮径向力的变化影响较小。在非设计流量工况下，随着间隙尺寸的增大，叶轮受到的径向力波动幅度逐渐增大，可能对轴流泵的稳定运行造成影响。