机器学习在橄榄石产地溯源中的应用
2024-01-25沈锡田张志清
仲 源,沈锡田,张志清,叶 敏,韩 禹
(1.中国地质大学(武汉)珠宝学院,湖北 武汉 430074; 2.湖北省珠宝工程技术研究中心,湖北 武汉 430074;3.湖北国土资源职业学院,湖北 武汉 430090; 4.张家口地质博物馆,河北 张家口 075000)
宝玉石的产地溯源常根据其包裹体特征[1]、谱学特征[2]和元素含量特征[3-5]等来判定。其中,元素含量特征常采用投图法,即用不同的元素或元素组合(和、差、比值等)构建坐标系,将不同产地的宝玉石样品的元素信息在其中投点,体现出差异化的分布。例如,通过Cr2O3/Ga2O3和Fe2O3/TiO2来区别变质型和岩浆型刚玉[3];通过Cs2O+K2O和FeO+MgO两个指标来区分不同产地的祖母绿[4];还可通过比较轻重稀土元素变化趋势以及异常稀土元素对出土古玉材料进行产地溯源[5]。但是实际产地判别中投图法仍存在一些局限性:(1)元素的选择基于经验,且判别过程依赖检测人员的视觉观察,存在一定主观性;(2)随着需要判别的产地增多,依赖少数几种元素构建的二维图像,容易出现不同产地的交叉重叠。例如,Ga-Zn-Li三种元素坐标系,阿富汗、赞比亚和巴西蓝宝石在该坐标系下的元素分布有部分重叠[4];(3)投图法依赖原始数据,复用性较差。
产地判别本质上是一种分类任务,机器学习能够从多维数据中自动学习规律、构建模型,从而进行分类,减少主观经验的介入,且具有较强的复用性。机器学习已经应用于很多领域如医疗影像诊断[6]、农作物产地溯源[7]等。其中,线性判别分析(LDA)已经在一些宝玉石产地研究中得到应用。Shen等[8]对四个产地的橄榄石样品进行了产地判别,利用了14种元素建立LDA模型;Giuliani等[9]根据不同原生矿床中的红、蓝宝石样品的成分建立了LDA模型,进而对次生矿床中的红、蓝宝石进行判别,推断其原生矿床来源;Zhang等[10]对吉林意气松和朝鲜的橄榄石样品进行对比研究,并采用了LDA对两个产地橄榄石样品进行了判别;Homkrajae等[11]基于LA-ICP-MS测出珍珠样品中的主微量元素含量,并利用LDA对三个产地的淡水珍珠样品进行了判别。其他机器学习算法(如决策树、随机森林、支持向量机、神经网络等)在宝玉石产地判别中的研究相对较少,且缺少对元素特征工程和模型优化的讨论研究。
本文研究以三个产地(河北大麻坪、吉林意气松、朝鲜长渊郡,各产地地理位置如图1所示)的橄榄石样品为研究对象,尝试在产地判别中应用多种机器学习算法,并探索优化产地判别模型的路径。我们通过LA-ICP-MS测试了河北橄榄石样品的元素含量,并结合了Zhang等[10]提供的吉林和朝鲜橄榄石样品的测试数据,使用Python语言和Scikit-learn机器学习库等进行了数据处理、分析和建模,分析了不同产地橄榄石样品的元素分布情况和各元素相关性,研究了元素的选择对于线性判别分析效果的影响,进而筛选合适的元素作为建模特征,同时采用了六种机器学习算法分别建立产地判别模型,对比了不同模型的准确性和泛化能力,从而对模型进行择优。
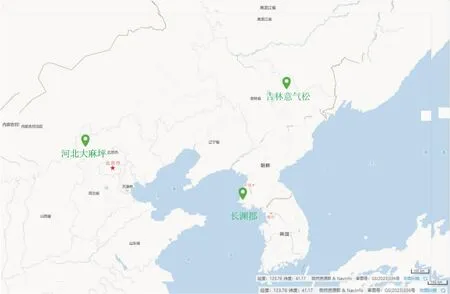
图1 河北大麻坪、吉林意气松和朝鲜长渊郡橄榄石样品的产地位置
1 样品及测试方法
1.1 样品情况
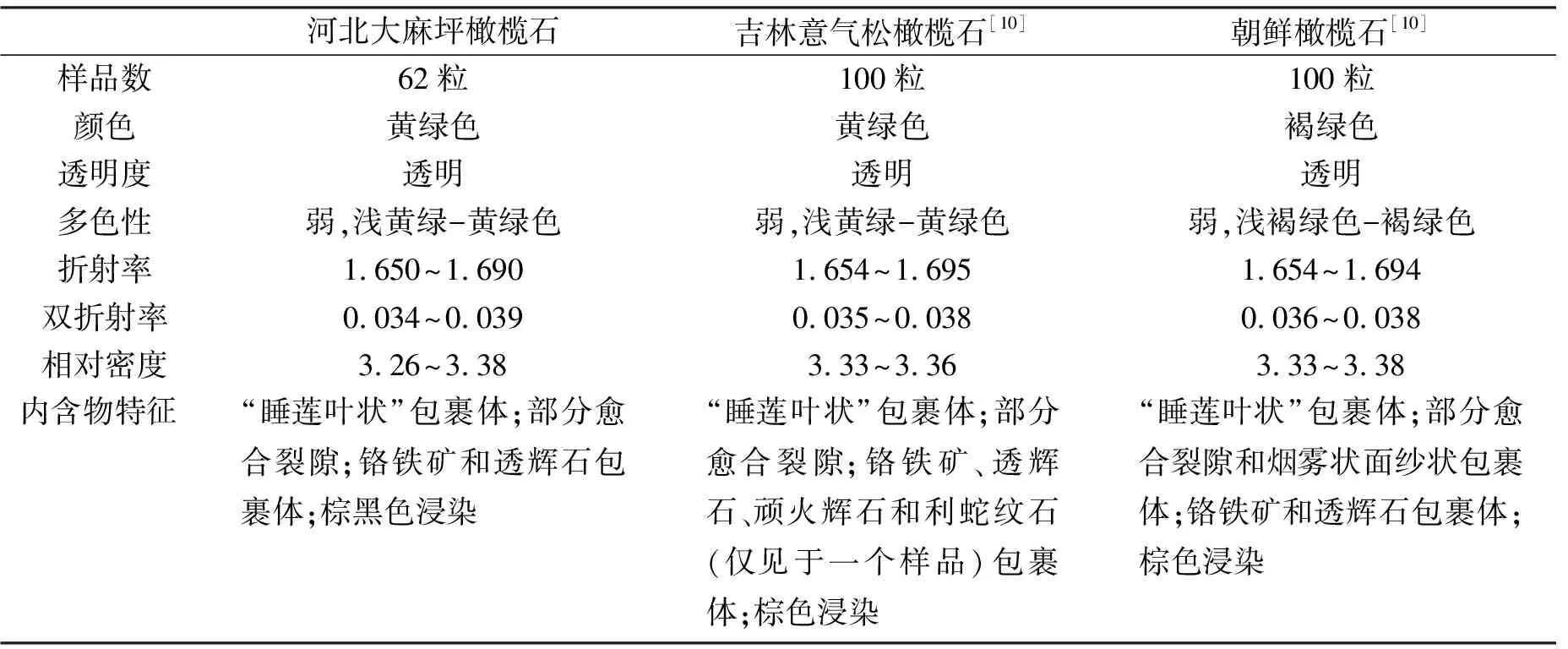
表1 三个产地橄榄石样品的常规宝石学特征

图2 河北大麻坪双面抛光后的部分橄榄石样品

图3 三个产地的橄榄石刻面成品(左三:河北大麻坪;中三:吉林意气松;右三:朝鲜长渊郡)
1.2 测试方法
河北大麻坪橄榄石样品均在武汉上谱分析科技有限责任公司的激光剥蚀电感耦合等离子体质谱(LA-ICP-MS)进行微区原位测试,仪器型号为与193 nm准分子激光剥蚀系统(GeoLasPro)联用的Agilent 7700 series ICP-MS。测试条件:激光器光束直径44 μm,频率5 Hz,能量80 J、能量密度为5.5 J/cm2、脉冲数250。选用美国地质调查局(USGS)制定的硅酸盐玻璃--2G、BCR-2G、BIR-1G作为标准样品。选用美国国家标准局 (NIST) 制定的标准参照样品SRM610校准时间漂移,每6个样品插入两个SRM610标样。为确保结果的可靠性,每个样品随机选取一个测试点且避开包裹体。此处需要说明的是,晶体本身均一性较好,未发现环带结构,且测试造成的误差可以看作是围绕样品真实值的随机噪声,而机器学习的建模过程更关心所有样品的整体分布情况,每个样品的随机噪声互相抵消,应对整体分布的均值影响不大。但模型的判别过程可能会对单一样品的误差敏感,因此后续研究和应用中可考虑增加单一样品的测试点位以提高判别精度。该测试条件和Zhang等[10]一致。
2 机器学习建模
2.1 编程语言和环境依赖
在Windows系统中,使用Python语言编程,采用JupyterLab集成开发环境,数据清洗、分析和建模主要依赖Pandas、NumPy、scikit-learn等库。
2.2 不同种类元素组合的线性判别分析
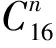
2.3 六种机器学习算法建模
对上文提及的65 519个LDA模型分别计算了准确率,其中交叉检验准确率最高的一个模型利用10种成分作为建模特征,分别为Mn、Zn、Na、Al、Sc、V、Cr、P、Ti和REE。在这10种成分的基础上,使用六种不同的机器学习算法建模,分别为LDA、基于高斯核函数的支持向量机(SVC-RBF)、基于拉普拉斯核的支持向量机(SVC-Laplc)、决策树(DTC)、随机森林(RFC)和反向传播神经网络(BPNN)。各算法及调用scikit-learn的接口参见表2。
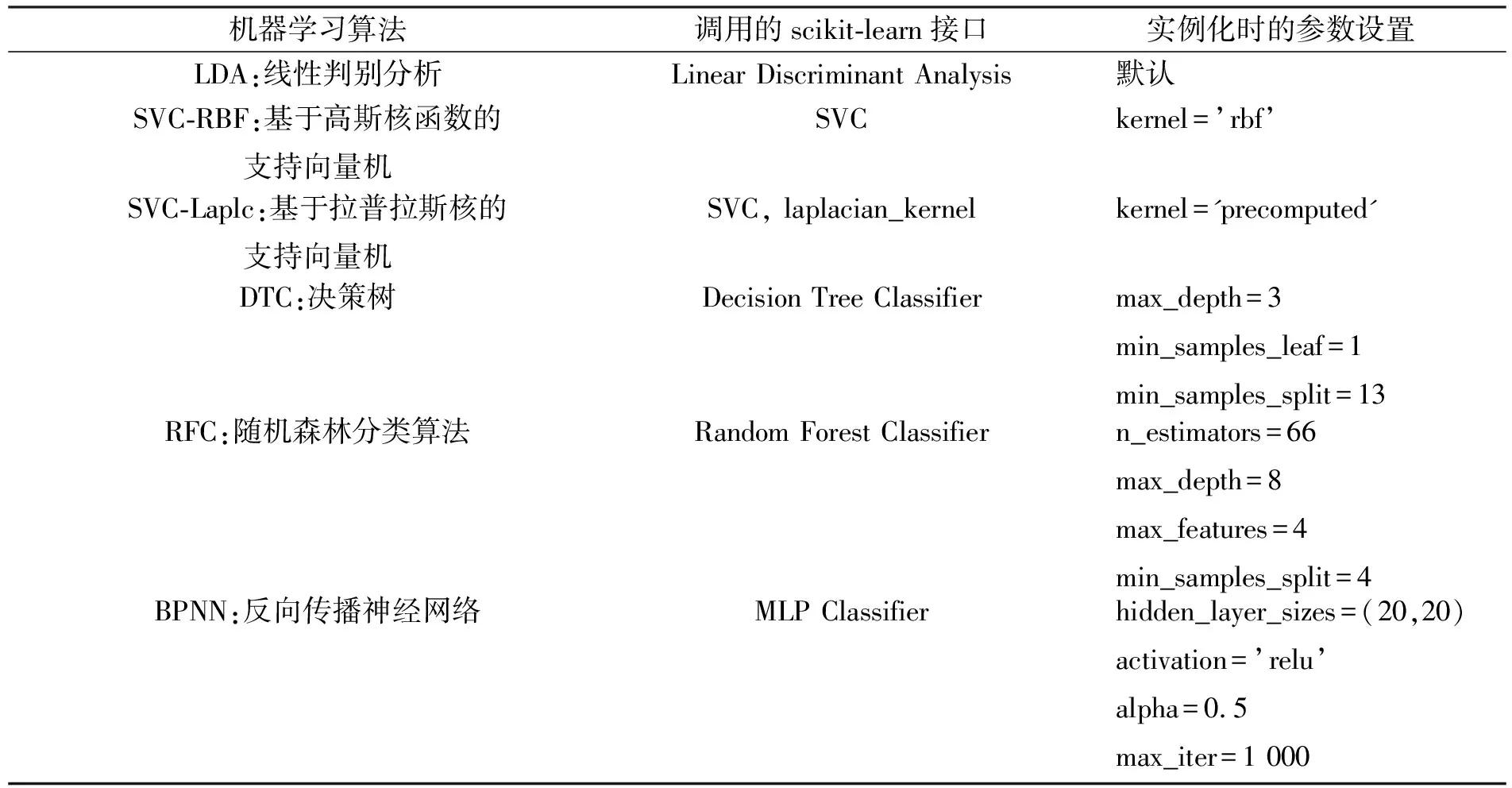
表2 六种机器学习算法调用的接口和参数设置
(1)SVC的主要思想是在特征空间中找到一个最优超平面,将不同类别的实例尽可能地分开,并且使得离超平面最近的训练样本(支持向量)到超平面的距离最大化,结合核函数,能够处理非线性可分的数据[12]。(2)DTC可将样本分类的过程用树形结构表示,一棵决策树由根节点、内部节点和叶子节点构成,其中根节点和每个内部节点表示对一种特征取值的判断,每个分支代表判断的结果,最后每个叶节点代表一种判别结果[13]。(3)RFC是一种结合了决策树和集成学习的机器学习算法,使用了集成学习中的Bagging算法,基本思想是从训练集中随机选择一定数量的子集,每个子集训练一棵决策树,多棵决策树投票最多的类别作为最终的输出[14]。(4)BPNN由三个部分构成:输入层、隐藏层和输出层,每层有一定数量的神经元,并按不同的权重分别与下一层各神经元进行多对多连接,就构成了网络结构。通过设计一个输出值和真实结果之间的误差函数,采用误差反向传播算法和梯度下降等的优化算法,不断调整神经元权重,迭代模型以缩小误差,从而找到一个最优化的模型[15]。(5)DTC和RFC模型采用网格搜索(Grid Search)的方式优化超参数。
全数据集准确率是用所有样品数据训练模型并回代入模型所得的预测结果,但是理想的模型不仅要在建模所用的数据上表现良好,也应该在其他数据上表现良好,即模型具有良好的泛化能力,因为建模的目的就是在未来实际检测中,对那些未知产地的样品也能做到有效的判别。因此,在本文,我们将数据集按训练集:测试集=7∶3的比例进行划分,并利用训练集训练模型,再分别代入训练集和测试集计算准确率。
3 结果和讨论
3.1 LA-ICP-MS分析
LA-ICP-MS测试结果(表3和表4)显示,高于检出限的成分有MgO、FeO、Li、Mn、Co、Ni、Zn、Na、Al、Ca、Sc、V、Cr、P、Ti、REE(Ca、Ti、REE有个别低于检出限的样品,按检出限/10进行了处理)16种。三个产地橄榄石样品的镁值Fo(nMg/nMg+nFe)基本在同一个范围内,属于高镁橄榄石。

表3 LA-ICP-MS测得的三个产地的橄榄石样品的主量成分
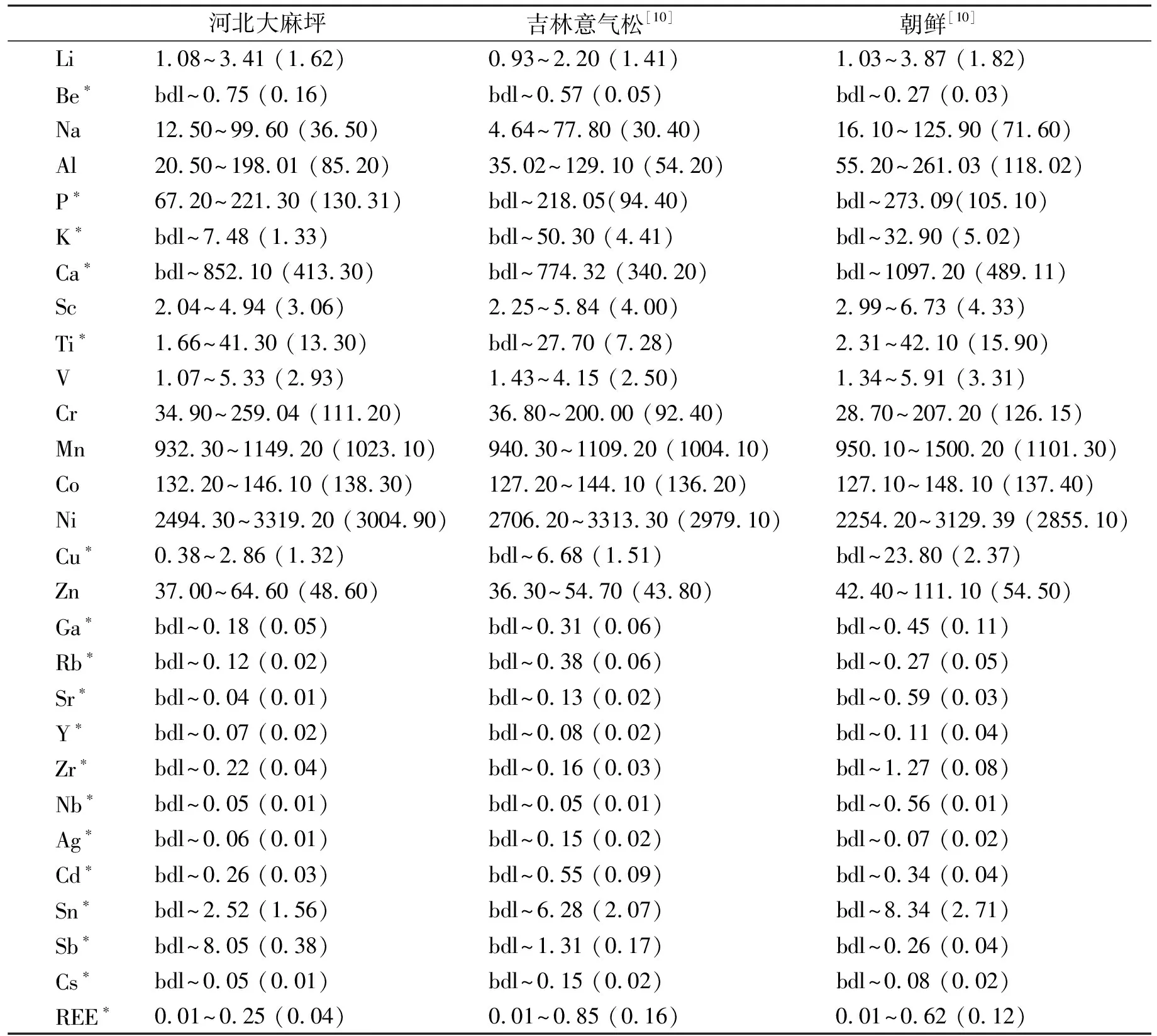
表4 LA-ICP-MS测得的三个产地的橄榄石样品的微量元素
图4通过核密度估计曲线展示了三个产地橄榄石样品在16种成分上的分布情况。整体上看,吉林橄榄石和朝鲜橄榄石样品的分布存在比较明显的差异,主要体现在Li、Na、Al、Ca、Ti、V、Cr、Mn、FeO、Zn共10个成分上,呈现出吉林橄榄石的含量偏低和朝鲜橄榄石的含量偏高的趋势。综合来看,吉林橄榄石和朝鲜橄榄石样品在多数成分上的差异较明显,在少数成分上难以区别(如Sc、P、REE等)。河北橄榄石与吉林和朝鲜橄榄石样品在大多数成分上都有所重叠,仅在个别成分上有一定的区别(如Al、Sc等)。
通水,不是简单的引水下山、接水入户,必须思虑周远,质效兼顾。在解决贫困地区农村安全饮水问题上,我省以管理制度改革为重点,不断探索。
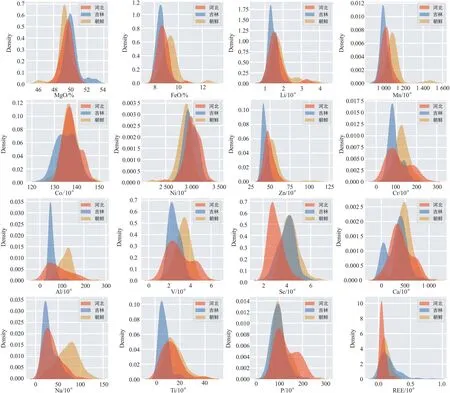
图4 三个产地橄榄石样品在16种成分上的高斯核密度估计
其他元素基本低于检出限,不列出;表3和表4括号内的值表示所有样品均值,低于检出限的样品按软件给出的原始数据作为其值;REE 表示稀土元素La~Lu的总量,低于检出限的取检出限的1/10作为其值;bdl 表示低于检出限;* 表示存在样品低于该元素检出限
3.2 通过线性判别分析优化化学成分组合
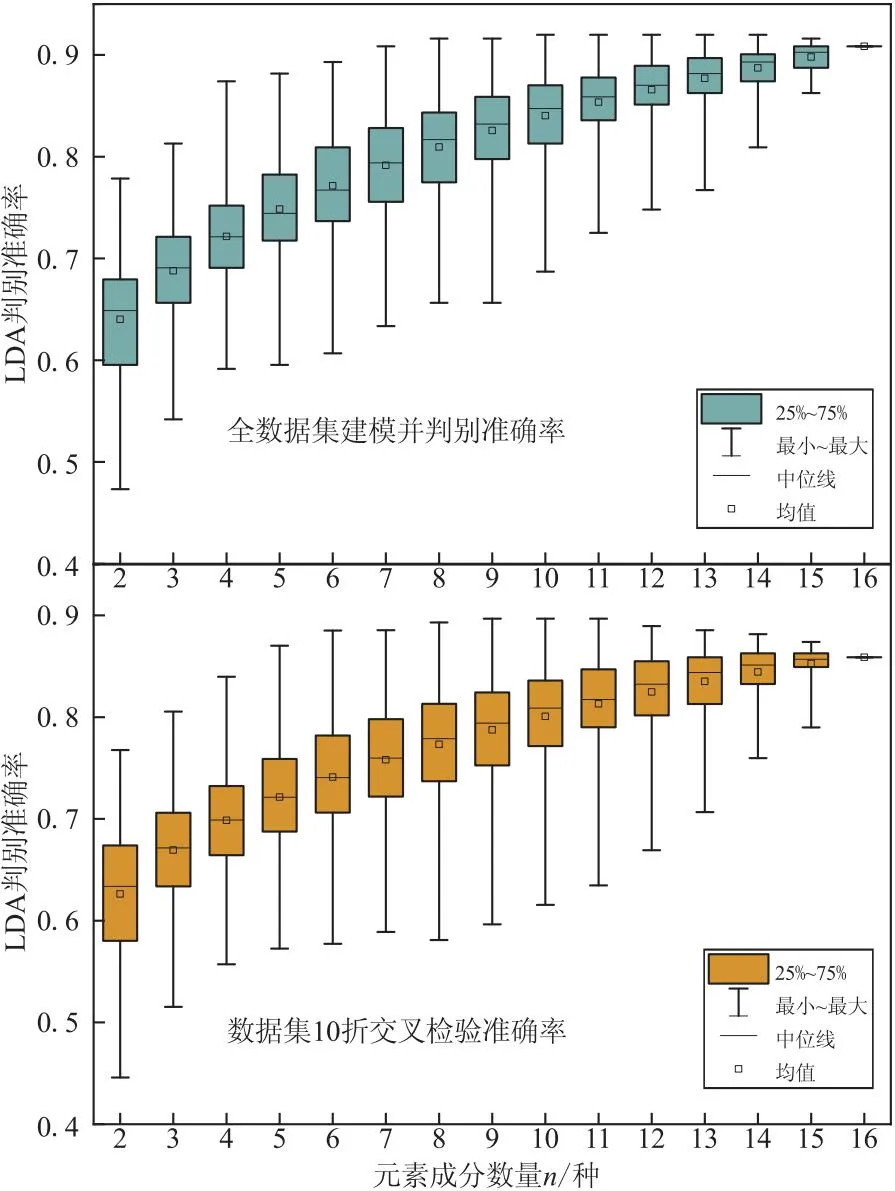
图5 不同数量的成分组合后建立LDA模型得到的准确率
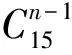
从图6可以看到,从3种成分组合开始,基本所有成分的平均改进度均为正值,这是因为2种成分组合的产地判别能力较差,基本上只要新成分加入,就能提供新的产地差异性特征,从而大幅提高判别准确率。随着组合中成分数量的增加,大多数成分的平均改进度呈下降趋势,甚至有个别成分(如MgO、FeO、Li、Mn、Ni等)从正值区间落到了负值区间,说明它们的加入降低了模型的准确率。
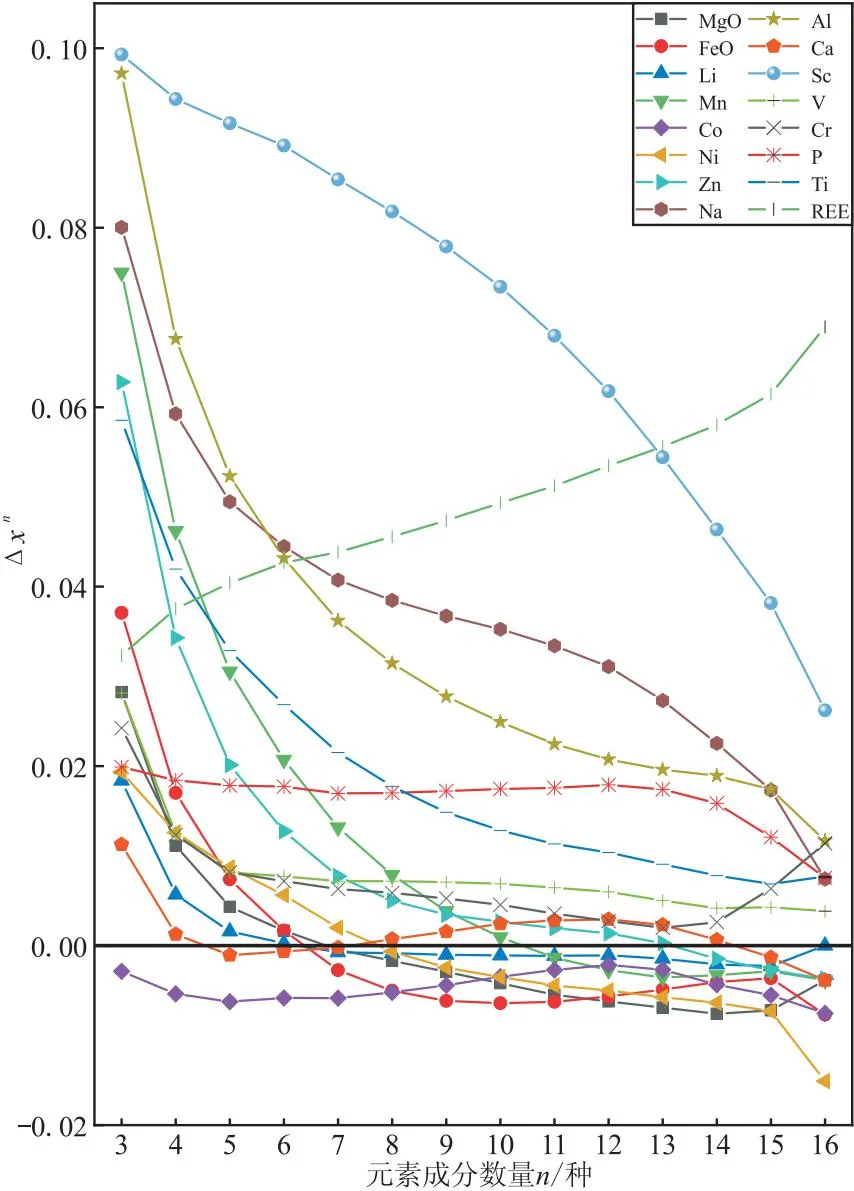
图6 不同数量成分组合中的平均改进度
Sc元素的平均改进度虽然呈下降趋势,但较之其他成分始终维持在较高的水平,说明它在产地判别中起到的作用是无可替代的。从图6可以发现,Sc元素是唯一可以明显看出河北和另外两个产地分布差异的成分,而其他成分在河北和另外两个产地都有大范围的重叠,所以Sc元素是区分河北橄榄石样品的关键。
P和Ca元素的平均改进度变化趋势比较类似,都是在小幅度的下跌后趋于平稳,随后又小幅上升,然后又下降。Ca在5~7、15~16种成分的时候平均改进度都跌到了负值。
REE的变化趋势最为特殊,始终呈上升趋势,从一开始的平均改进度处于一个平均的水平,到最后超过Sc元素成为平均改进度最高的元素。
Co元素的平均改进度始终处于负值区间,这说明Co大多情况下起到了降低准确率的作用,从图4也可以看到Co在三个产地上的分布没有明显的区分。
为了对这些成分的平均改进度进行一个比较,将各成分从3种到16种成分组合的平均改进度分别进行加和(图7),可以看到MgO、Co、Ni平均改进度总和均为负值,说明这3种成分在组合的成分数量变化过程中整体上对准确率起负面影响,之后的模型中将直接剔除这3种成分。FeO、Li、Ca的平均改进度总和相较其他成分很低,对准确率基本没有贡献,且从Li和Ca的产地分布上看,它们产地差异性也很小,也可以考虑剔除。剩下10种成分(Mn、Zn、Na、Al、Sc、V、Cr、P、Ti、REE)的平均改进度总和都较高,这10种成分组合的模型全数据集准确率为0.908,交叉检验准确率为0.889。
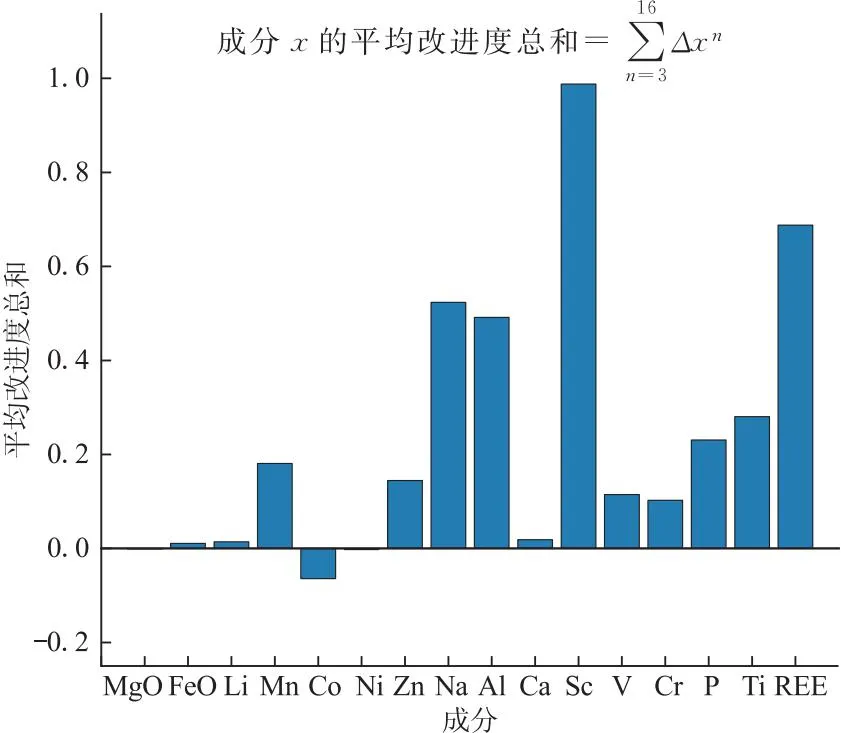
图7 各成分平均改进度总和
De Hoog等[17]将橄榄石中的微量元素分为三类,不同的类别具有不同分配规律和含量特征:(1)I类元素(Li、Mn、Co、Ni、Cu、Zn)中,除了Li和Cu外,其它元素的离子半径接近于Mg的半径,且价态也是二价,所以容易进入晶格,常显示出与Fo的相关性。I类元素含量变化小,在地幔橄榄岩中,这些元素主要富集于橄榄石,其含量取决于熔体的总含量,且受橄榄石平衡温度的影响小。(2)Ⅱ类元素(Cr、Al、V、Sc、Ca、Na)受离子电价和尺寸的影响,不易进入橄榄石晶格中,但更容易进入其它共生矿物(如尖晶石、辉石等)中。Ⅱ类元素的含量变化明显,主要受到平衡熔体温度及共生矿物相的控制。(3)Ⅲ类元素(Ti、Zr、Nb、Y、P、REE)中,除了P外,其它元素的含量变化很大,主要受熔体总含量影响。在地幔橄榄岩的平衡温度下,受到离子电荷和尺寸的影响,Ⅲ类元素不易进入橄榄石晶格,也不易进入其他共生矿物中,因此会和其他共生矿物显示相似的含量变化。
改进度较高的10种成分中,Mn和Zn属于I类元素,Na、Sc、V、Cr属于Ⅱ类元素,P、Ti、REE属于Ⅲ类元素,说明该模型充分利用到了De Hoog等[17]所说的三类元素,能更全面地反应出产地的差异化特征。
综上所述,成分数量较少的情况下,新增成分一般对于模型准确率有很大提升,具体来说就是引入了异类元素。从数学的角度上,异类元素相关性小、产地分布差异大;从地质角度上,是因为异类元素携带了不同地质环境种的物理条件和元素丰度的信息。但当元素数量过多时,新增元素很可能导致模型准确率下降,可能是某些元素在加入时给模型引入了一些不必要的噪声,如主量成分MgO、FeO在三个产地橄榄石间的差异本来就不大,加入它们不能提升模型性能,反而可能让模型过拟合。
3.3 六种机器学习算法对比结果分析
LDA是在高维空间中寻找超平面将不同类别的样本切分开,但当不同类别的样本在高维空间中的分类边界不是平面而是曲面时,线性判别的效果就会差很多,甚至产生大量的误判。仅以二维空间中的二分类问题为例,如图8,随机生成3种分布形态的数据A、B、C,模拟可能出现的二分类情况。A中两类样本大致呈左右对称的分布,B中两类呈月牙形、相互嵌套构成弯曲边界,C中两类呈同心圆分布。
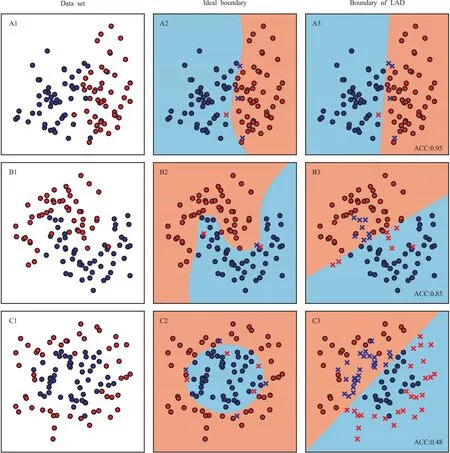
图8 二维空间中的二分类问题样本分布的理想边界和LDA边界
图8-A2/B2/C2表示了理想边界,即真实环境中总体之间的边界,可能存在一些噪声(用“x”表示)。通过LDA建模得到了图8-A3/B3/C3的分类边界。对于A中的数据,LDA表现较好,能将大部分样本正确地分类,准确率为0.95。对于B中的数据,红蓝区域两类数据边界是弯曲镶嵌,无法找到一条可以完美分割两类的直线,LDA划分出的两个区域中必然会残留对方的样本,这使得LDA准确率降低到0.85。对于C类同心圆型数据,LDA判别准确率只有0.48,这样的判别没有意义。LDA往往要建立在样本正态分布以及协方差相等的假设的基础上。可见,在不知道数据分布形态的情况下,使用LDA不一定能得到准确率较高的模型,而非线性的算法可能会更有优势。
我们基于3.2节推荐的10种成分(Mn、Zn、Na、Al、Sc、V、Cr、P、Ti、REE),分别应用六种机器学习算法建模,并计算测试集准确率和训练集准确率(图9)。其中,(1)LDA在训练集上的准确率比较低,在测试集上的准确率最低;(2)SVC(RBF)和SVC(Laplc)的训练集准确率和测试集准确率属于中等水平;(3)DTC在训练集上的准确率比LDA还要低一些,说明对训练集的学习非常不足,在测试集上的准确率比LDA高一些,训练集和测试集准确率差值较低;(4)RFC在训练集上得到了100%的准确率,但在测试集上准确率下降到0.848,说明模型可能对训练集过拟合的程度比较高;(6)BPNN在训练集上的准确率是除了RFC之外最高的,且在测试集上也取得了最高的准确率,这说明该模型即从训练集中充分学习到了训练集的特征,而且也学习到了更普遍的产地特征,具有较强的泛化能力,在未知样本上也有能力进行较准确产地判别。但该算法存在一定随机性,每次生成模型的准确率有所波动,准确率是取50次训练结果的平均值,其中训练集准确率1个标准差为 0.01,测试集准确率1个标准差为0.015。
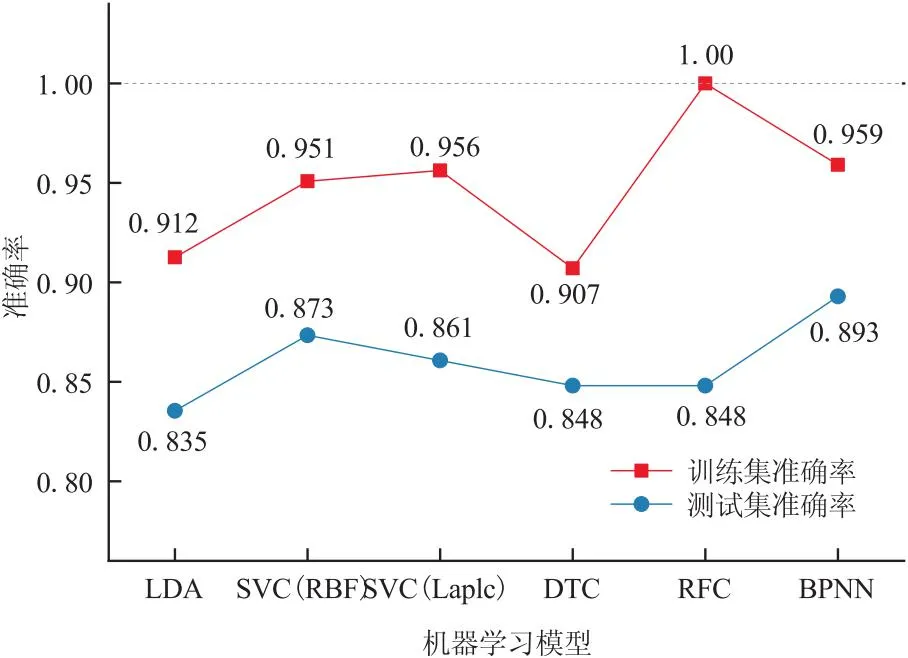
图9 六种机器学习模型在橄榄石训练集和测试集上的准确率
综上所述,对于河北、吉林和朝鲜三个产地橄榄石样品的判别,大部分非线性算法(除了DTC)相较LDA,准确率都有了提升,其中BPNN准确率最高,SVC训练结果稳定且准确率较高。
4 结论
本文以河北、吉林和朝鲜三个产地橄榄石样品为例,筛选10种化学成分(Mn、Zn、Na、Al、Sc、V、Cr、P、Ti、REE)作为特征,使用六种机器学习方法进行产地判别,得到如下主要结论。
(1)应用支持向量机等非线性的机器学习算法建模可以得到较好的判别效果,训练集准确率可以达到95%以上,测试集准确率可以达到86%以上,远超传统的基于全部元素的LDA模型。
(2)筛选元素的意义在于提取出了能够更好表现产地差异化性质的信息,剔除了冗余和无关的噪声,能提升模型的性能和训练效率。
