负压厂房事故后压力动态变化研究

薛 宇 赵 丹

(上海核工程研究设计院股份有限公司,上海)

0 引言

在工业生产活动中,可能会产生对人体有害的放射性物质,为防止放射性空气及气溶胶无控制地向室外逸散,必须通过排风维持室内的负压环境[1]。事故工况下,大量带放射性物质泄漏会造成室内压力快速突增,破坏负压平衡。因此,需要对事故工况进行分析研究,得到房间压力的逐时变化数据,用于指导类似负压厂房事故排风设计。

事故通风目前被大量应用于地下综合管廊及制冷机房通风设计中[2-4],学者们通过模拟事故工况,得到了较优的气流组织方案,可以减少事故危害。张倩茹等人对氨制冷机房发生泄漏时的排风口位置进行了优化设计,并指出房间门窗设置对氨气排除有较大影响[5];王雪梅等人对管廊燃气泄漏扩散进行了模拟,得到了不同泄漏孔径下所需的事故通风换气次数[6]。室内有害气体泄漏研究主要集中于天然气泄漏的模拟与实验分析,并得到了对应的扩散模型[7-9]。陈琪对室内天然气管道泄漏扩散特性进行了研究,得到了甲烷滞留区范围,可用于指导事故现场检测[10];于晓龙对不锈钢波纹管内的天然气泄漏进行了理论研究,得到了泄漏管段压力与泄漏量的关系式[11]。目前研究多集中于易燃易爆物质泄漏后的检测与通风排除,对于带放射性物质泄漏过程中房间压力变化的研究较少。

本文对负压厂房内物质发生泄漏后房间压力的变化进行理论与模拟研究,分析物质泄漏过程中房间的压力变化及泄漏物质扩散情况,并计算房间恢复到初始状态所需时间,为类似负压厂房事故排风设计提供参考。

1 理论计算

1.1 负压变化计算

负压厂房日常工况下,室内开启排风机(风量2 000 m3/h)维持-30 Pa的负压,室外空气由门缝渗透进入室内;事故工况下,内部带放射性高温水泄漏,室内短时间内达到正压,室内带放射性气体由门缝排至室外。理论计算过程中进行了以下假设简化:

1) 室内空气为理想气体;

2) 室外气压为标准大气压;

3) 室内初始温度为26 ℃;

4) 破口泄漏流量恒定为28 kg/s,泄漏时长为24 s;

5) 破口高温水泄漏的同时会产生气体闪蒸,闪蒸率γ为40%;

6) 建筑物与环境没有换热;

7) 假设24 s后室内空气温度不再下降。

整个事故过程可以分为3个阶段:0～24 s室内压力不断上升,24 s时室内达到最大正压;受排风与门缝漏风影响,室内压力与外界大气压达到平衡;排风机继续运行,室内转为负压,门缝处空气流向转变,向室内补风,最终室内压力恢复至-30 Pa。

使用理想气体状态方程与换热公式进行室内压力变化的动态计算,得到以下计算公式。

(1)

(2)

Q1=Qmγr+(100-26)Qmc1

(3)

(4)

tτ=t(τ-1)+Δt1(τ≤24 s)

(5)

tτ=t24(τ>24 s)

(6)

(7)

(8)

式(1)～(8)中n1为破口高温水摩尔质量流速,mol/s;Qm为破口高温水泄漏流量,kg/s;μ2为水蒸气摩尔质量,kg/mol;n2为排风口空气摩尔质量流速,mol/s;ρa为空气密度,kg/m3;Qv1为室内排风机流量,kg/s;μ1为空气摩尔质量,kg/mol;Q1为破口高温水每秒对室内输入的热量,kW;r为水的汽化潜热,kJ/kg,取2 257.2 kJ/kg;c1为水的比热容,kJ/(kg·℃),取4.2 kJ/(kg·℃);Δt1为Q1单位时间内对室内温度的提升,℃;V1为室内空间体积,m3;c2为空气的比热容,kJ/(kg·℃),取1.012 kJ/(kg·℃);t为室内温度,℃;n′为门缝处空气摩尔流量,mol/s;Q为门缝处空气流量,m3/h;p为室内压力,Pa;n为室内空气物质的量,mol;下标τ为时间,s。

根据经验公式,门缝处空气流量Qτ为

(9)

式中 1.03为混凝土拼缝接缝等的附加泄漏量系数;A为门缝有效漏风面积,m2;Δp为室内外压差,Pa;z为指数,一般取2;1.25为不严密处附加系数;N2为漏风疏散门数量。

采用式(1)～(9)进行700 s的逐时计算,得到室内压力的动态变化,并绘制室内压力随时间的变化曲线及门缝处空气流量随时间的变化曲线,如图1、2所示。

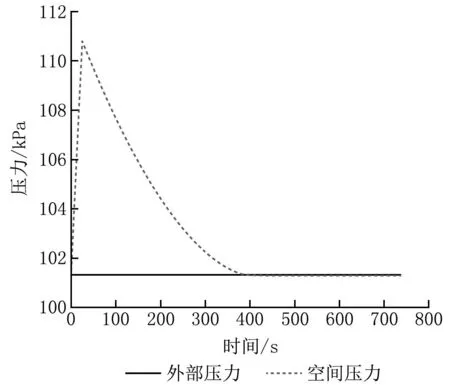
图1 室内压力随时间的变化

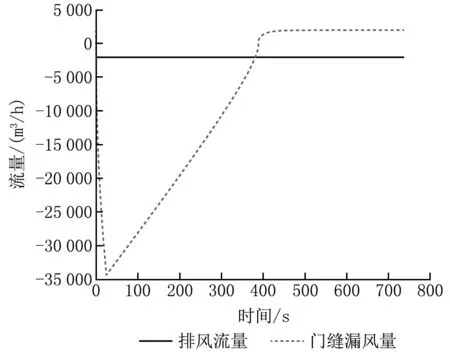
图2 门缝处空气流量随时间的变化

计算可知,24 s时,室内达到最高压力,为110.800 kPa,表压为9.480 kPa,室内压力增大9.505 kPa,此时门缝处空气流量最高,为34 252 m3/h。390 s时,室内外压差为0 Pa,448 s时,室内外压差重新变为-30 Pa。

0～24 s时,由于室内压力远大于室外,门缝处空气流向为由室内向室外扩散,且于24 s达到空气流量峰值,为34 169 m3/h;24 s后室内压力逐步降低,内外压差缩小;390 s时,室内压力与外部压力相等,门缝处空气流量为0 m3/h;390 s后,室内变为负压状态,门缝处空气流向发生转换,至448 s时,室内与室外压差恢复最初状态,为-30 Pa,门缝处空气流量也达到稳定,为2 000 m3/h。

1.2 参数敏感性分析

研究排风量、泄漏水与空气的换热量、门缝面积对室内压力动态变化的影响。

调整排风量参数分别为2 000、5 000、10 000 m3/h,对比各工况下室内压力峰值及门缝处空气流量变化情况,得到对应的恢复负压所需时间,如图3、4所示。

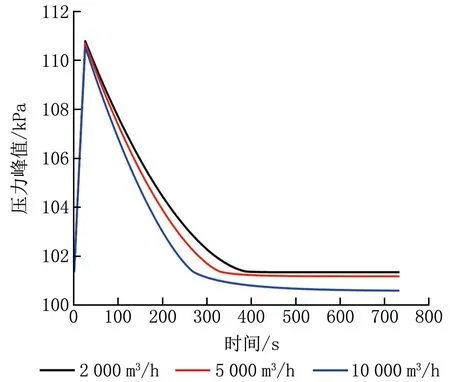
图3 不同排风量下室内压力峰值随时间的变化

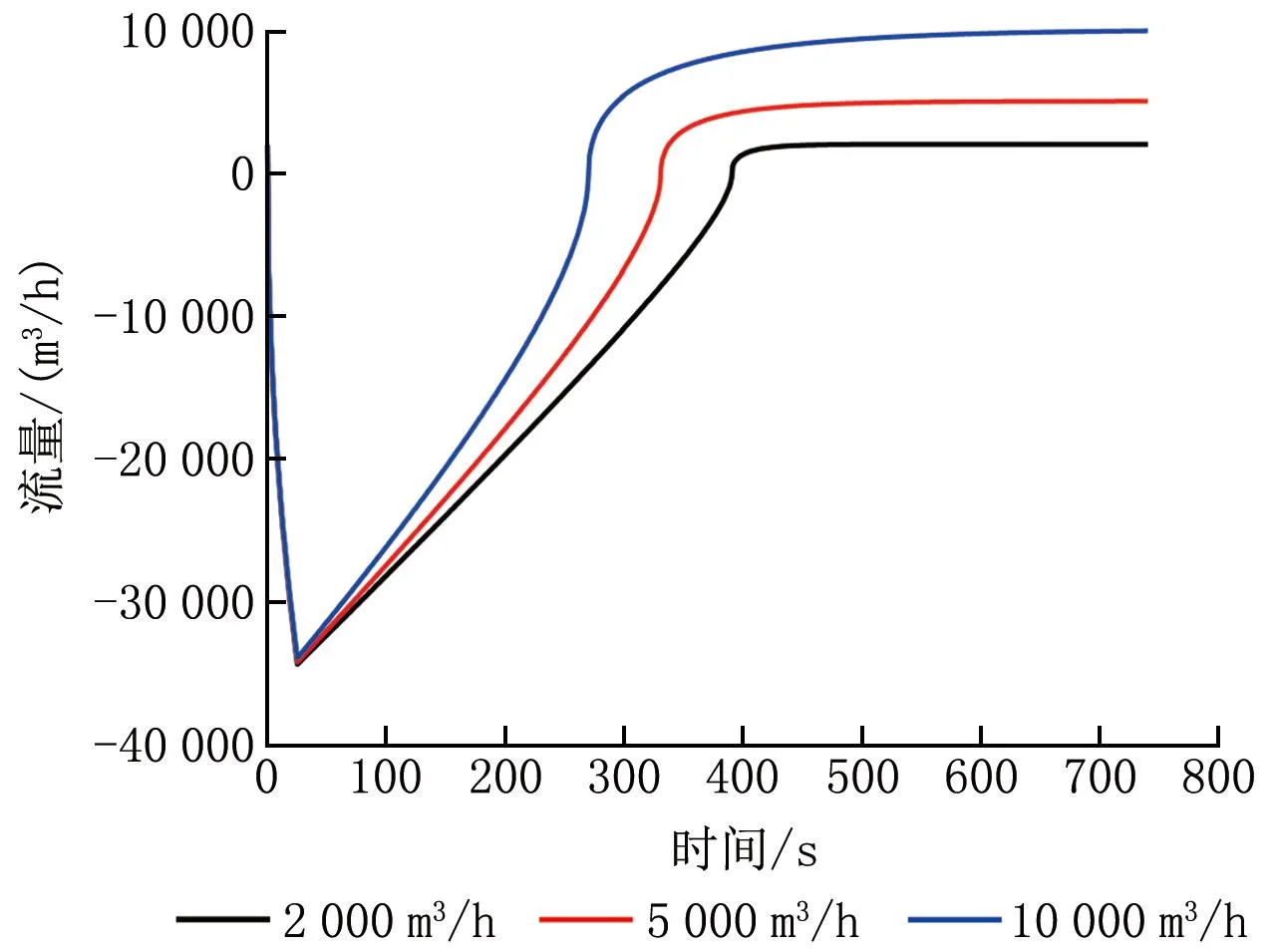
图4 不同排风量下门缝处空气流量随时间的变化

由图3、4可知,增大排风量可降低室内压力峰值,并缩短室内恢复负压所需时间。排风量为5 000 m3/h时,室内压力峰值为110.436 kPa,室内外压差为9.111 kPa,恢复负压所需时间为337 s;排风量增大为10 000 m3/h时,室内压力峰值为110.204 kPa,室内外压差为8.879 kPa,恢复负压所需时间为273 s。排风量增大150%,室内压力峰值仅减小0.08%,恢复负压所需时间缩短24.7%;排风量增大400%,室内压力峰值仅减小0.21%,恢复负压所需时间缩短39.0%。排风量增大对室内压力影响较小。

调整泄漏水的温度分别为30、50、75、100 ℃,对比各工况下室内压力峰值及门缝处空气流量变化情况,得到对应的恢复负压所需时间,如图5、6所示。

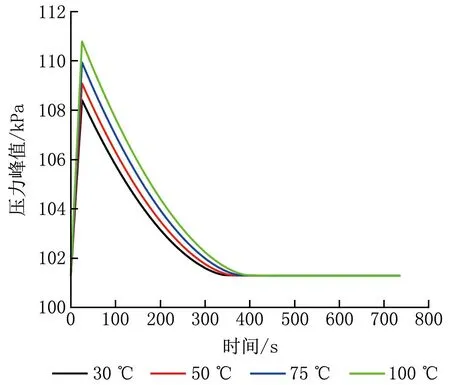
图5 不同泄漏水温度下室内压力峰值随时间的变化

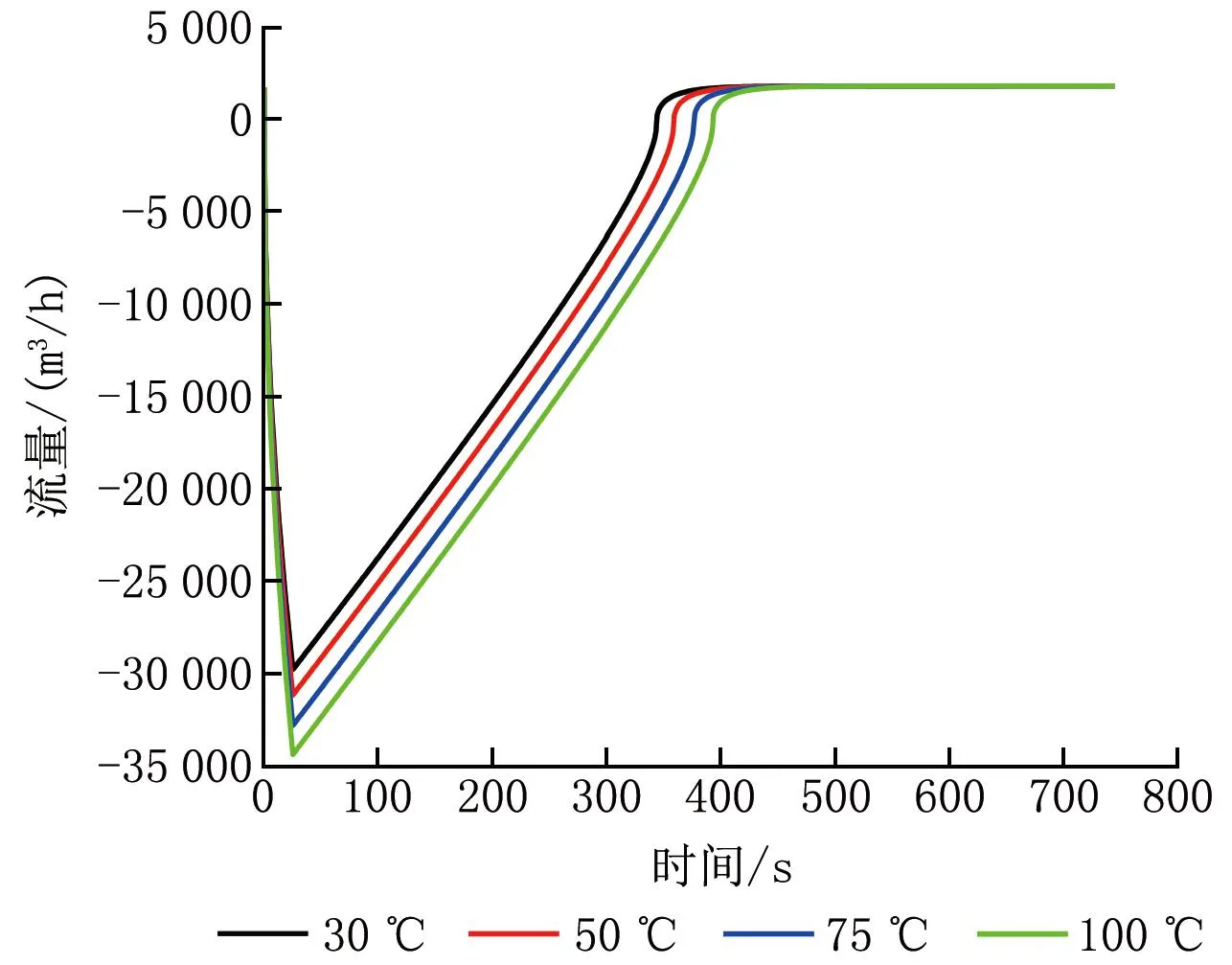
图6 不同泄漏水温度下门缝处空气流量随时间的变化

由图5、6可知,泄漏水温度对室内压力峰值和恢复负压所需时间的影响较大。泄漏水温度为30 ℃时,室内压力峰值为108.422 kPa,室内外压差为7.097 kPa,恢复负压所需时间为401 s;泄漏水温度为50 ℃时,室内压力峰值为109.100 kPa,室内外压差为7.775 kPa,恢复负压所需时间为416 s;泄漏水温度为75 ℃时,室内压力峰值为109.949 kPa,室内外压差为8.624 kPa,恢复负压所需时间为433 s。泄漏水温度降低25%,室内压力峰值减小0.77%,恢复负压所需时间缩短3.3%;泄漏水温度降低50%,室内压力峰值减小1.50%,恢复负压所需时间缩短7.1%。泄漏水与空气的换热量对室内压力峰值影响较大,对恢复负压所需时间影响较小。

调整门缝漏风面积分别为初始面积的2倍、5倍,对比各工况下室内压力峰值及门缝处空气流量变化情况,得到对应的恢复负压所需时间,如图7、8所示。

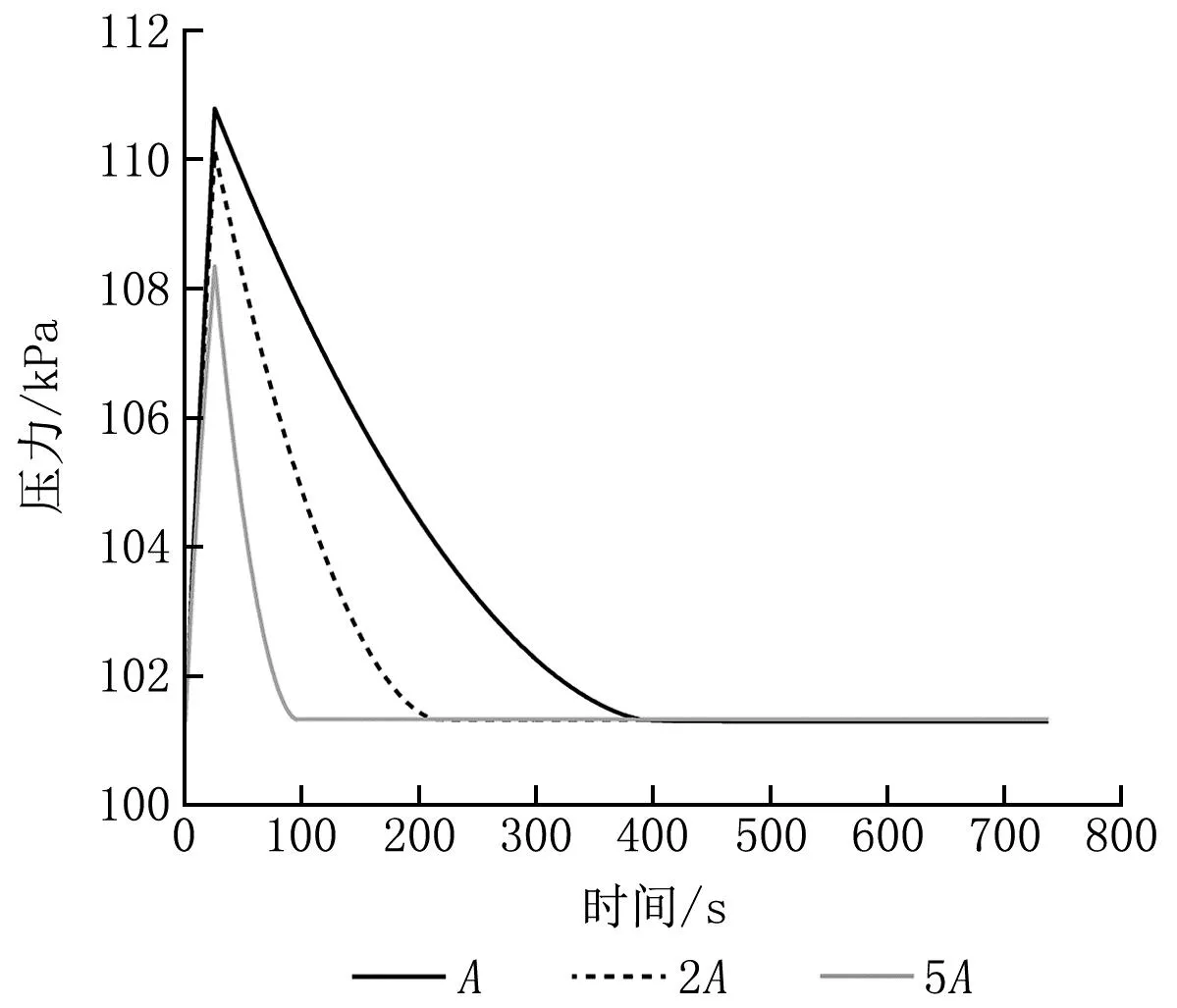
图7 不同门缝漏风面积下室内压力随时间的变化

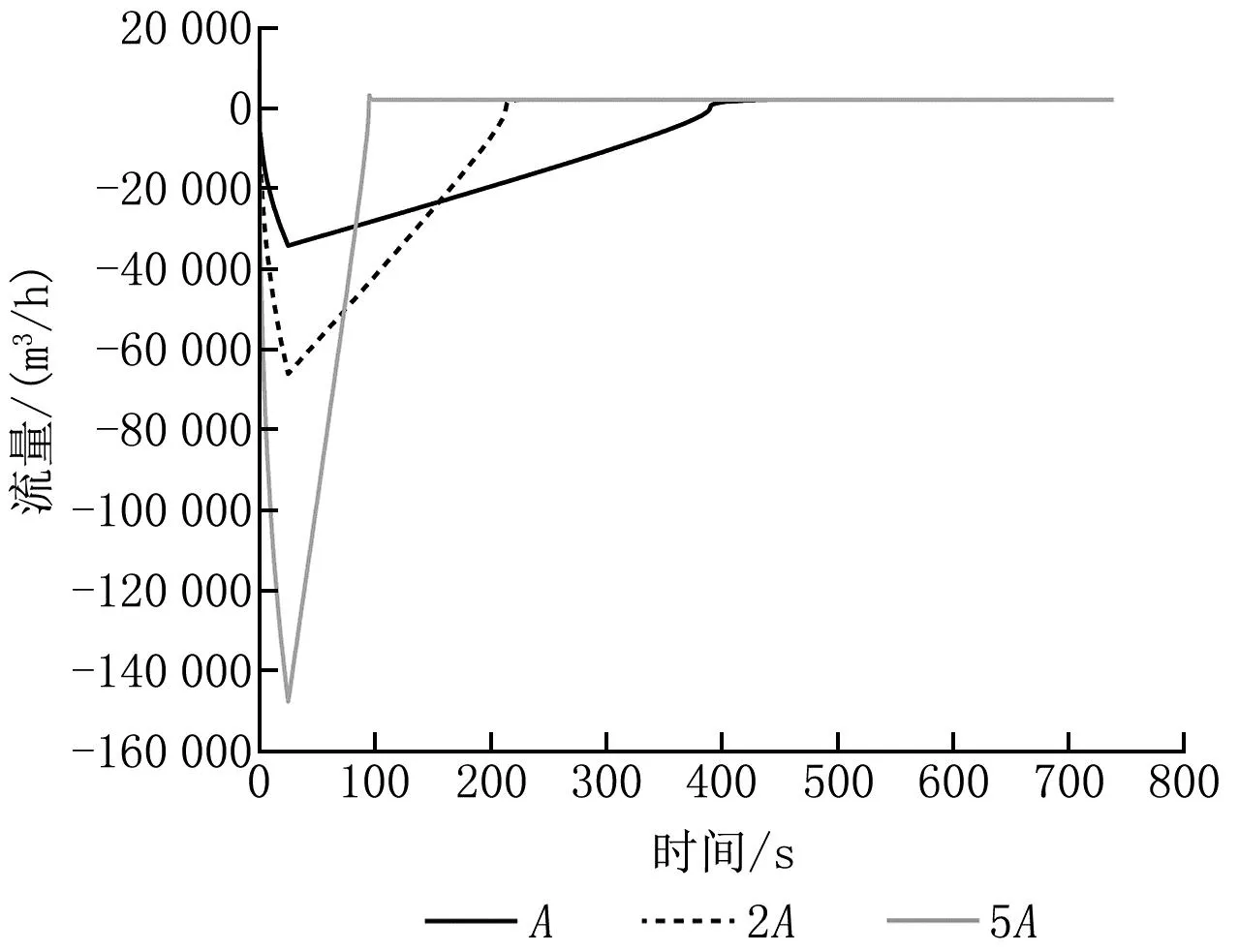
图8 不同门缝漏风面积下门缝处空气流量随时间的变化

由图7、8可知,门缝面积对室内压力峰值和恢复负压所需时间影响较大,门缝面积为初始面积的2倍时,室内压力峰值为110.136 kPa,室内外压差为8.489 kPa,恢复负压所需时间为244 s,室内压力峰值减小0.59%,恢复负压所需时间缩短54%;门缝面积为初始面积的5倍时,室内压力峰值为108.346 kPa,室内外压差为7.021 kPa,恢复负压所需时间为97 s,室内压力峰值减小1.30%,恢复负压所需时间缩短78%。门缝面积对室内恢复负压所需时间影响较大,即室内有较多与外界连通的门时,恢度负压所需时间会大幅缩短;门缝面积对室内压力峰值影响较小。

2 数值模拟计算

2.1 几何模型

建立负压厂房简化模型,如图9所示。中部为高温水蒸气储罐,事故工况下储罐顶部出现直径30 mm的泄漏点。排风口尺寸为500 mm×400 mm,位于储罐单侧,中心标高10 m。

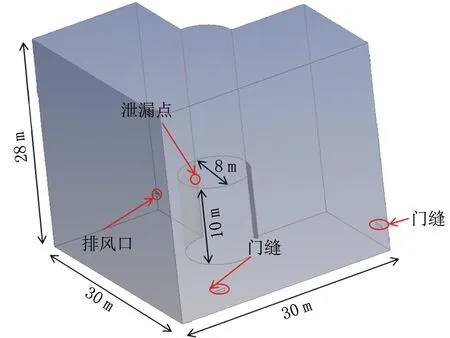
图9 负压厂房简化模型

采用ANSYS Fluent软件进行模拟计算,采用Meshing进行网格划分,对送风口与门缝进行加密,并完成网格独立性检验。采用非稳态计算,考虑重力,采用标准K-ε模型及组分运输模型,设置混合物为不可压缩理想气体。边界条件见表1。

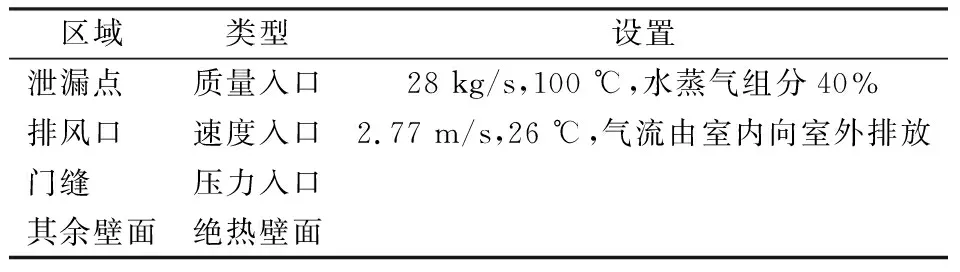
表1 边界条件设置

2.2 0～24 s时段的模拟计算

24 s时的室内水蒸气质量分数分布如图10所示。粒子在24 s内会充斥整个房间,且可以到达门缝位置,向外溢出。24 s时,室内水蒸气平均质量分数为2.7%。泄漏点附近水蒸气质量分数较高,其余位置分布较均匀。

图10 24 s时水蒸气质量分数分布

选取特殊截面进行分析。平面1为2.5 m高度处的水平截面;平面2为排风口处的竖直截面。平面1的压力分布云图与水蒸气质量分数分布如图11、12所示。

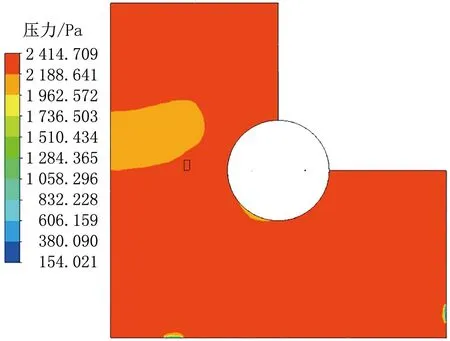
图11 24 s时平面1的压力分布云图

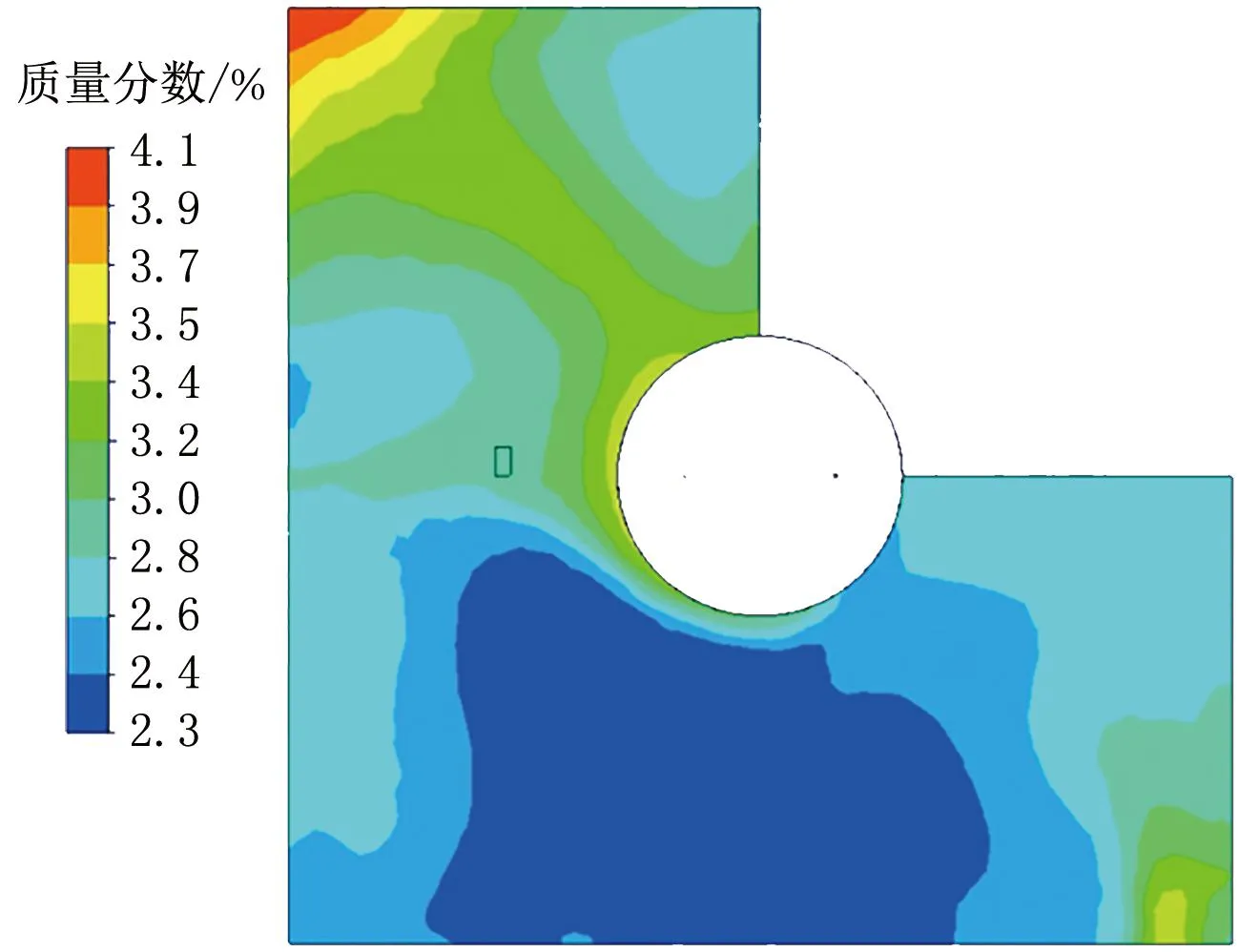
图12 24 s时平面1的水蒸气质量分数分布云图

24 s时,平面1压力分布大致均匀,基本维持在2 400 Pa左右,但门缝附近会存在压力的梯度变化,这是由于门缝附近存在流体向外流出。内外压差峰值为2 414 Pa。平面1水蒸气质量分数基本维持在3.0%左右,房间角落位置存在循环死角,质量分数较大,门缝附近质量分数较小。

平面2压力分布与水蒸气质量分布如图13、14所示。

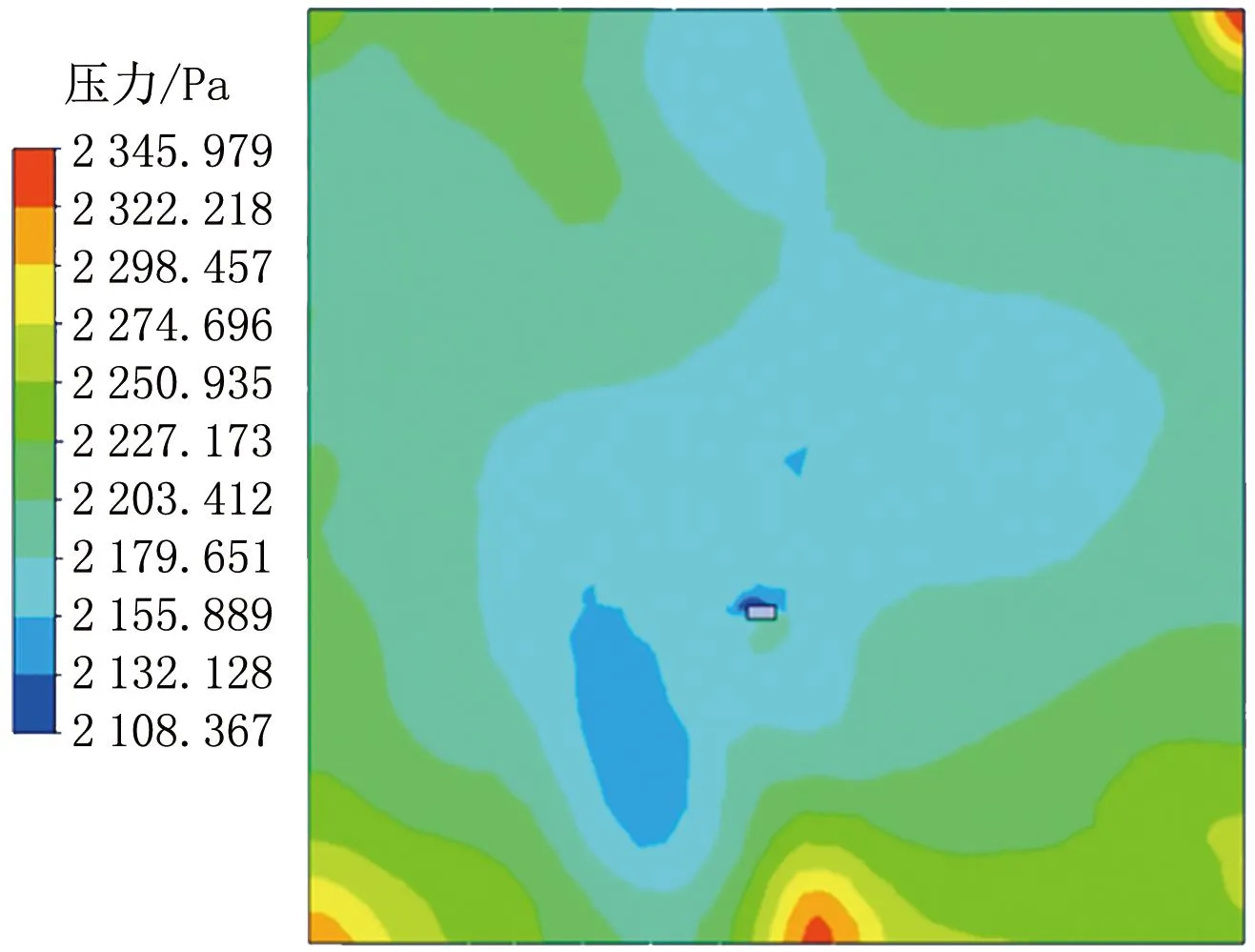
图13 24 s时平面2的压力分布云图

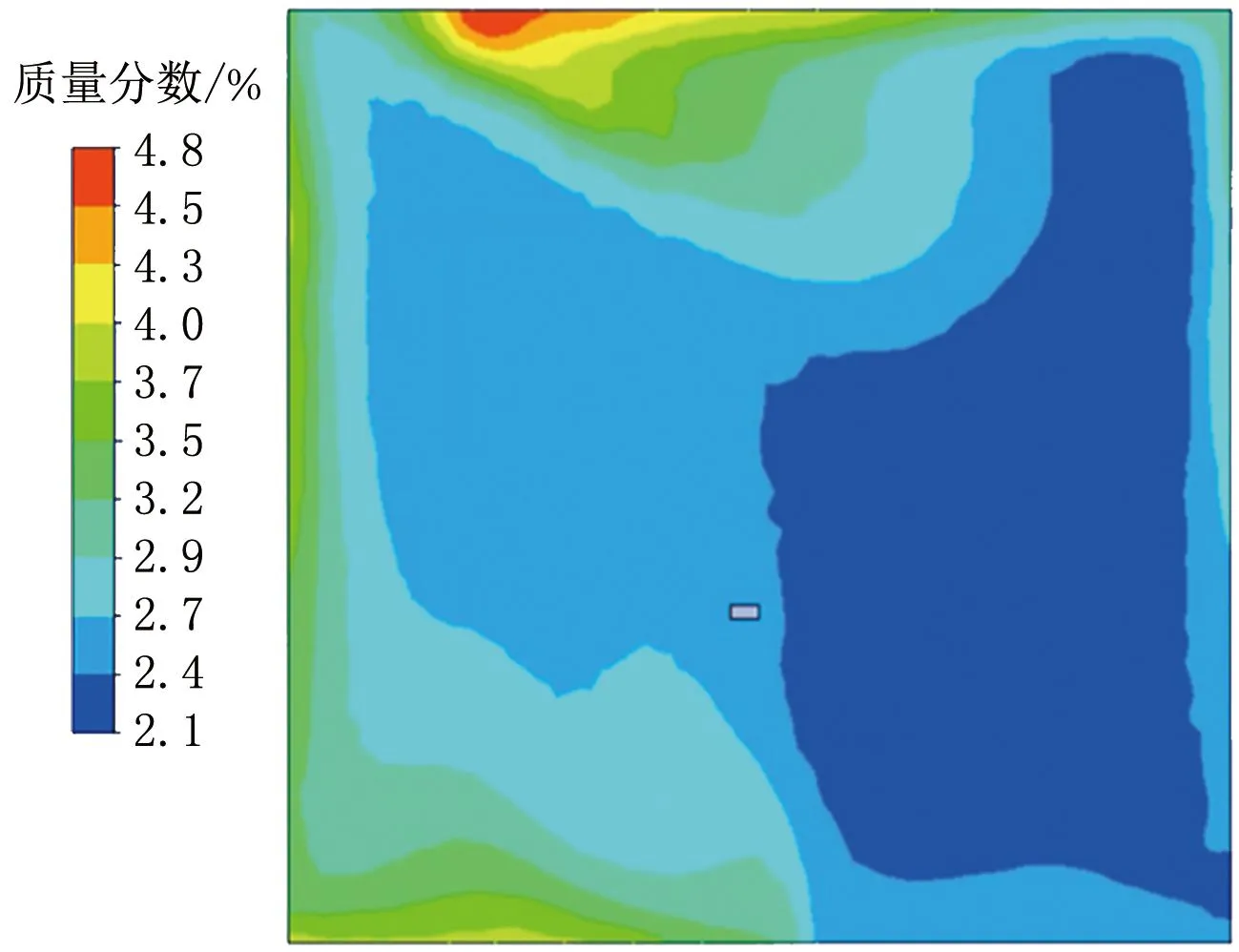
图14 24 s时平面2的水蒸气质量分数分布云图

24 s时,平面2压力分布基本均匀,均为高压状态,压力基本维持在2 200 Pa左右,排风口附近压力较低,角落处存在循环死角,压力较高。门缝附近水蒸气质量分数较小,这是由于水蒸气持续向外排除导致的。

2.3 24～234 s时段的模拟计算

24 s之后,关闭泄漏点的入口,继续模拟至234 s。234 s时的室内水蒸气质量分数分布如图15所示。234 s时室内水蒸气质量分数平均为2.0%,较24 s时有所下降,且分布较均匀。

图15 234 s时水蒸气质量分数分布

234 s时平面1压力分布与水蒸气质量分数分布如图16、17所示。

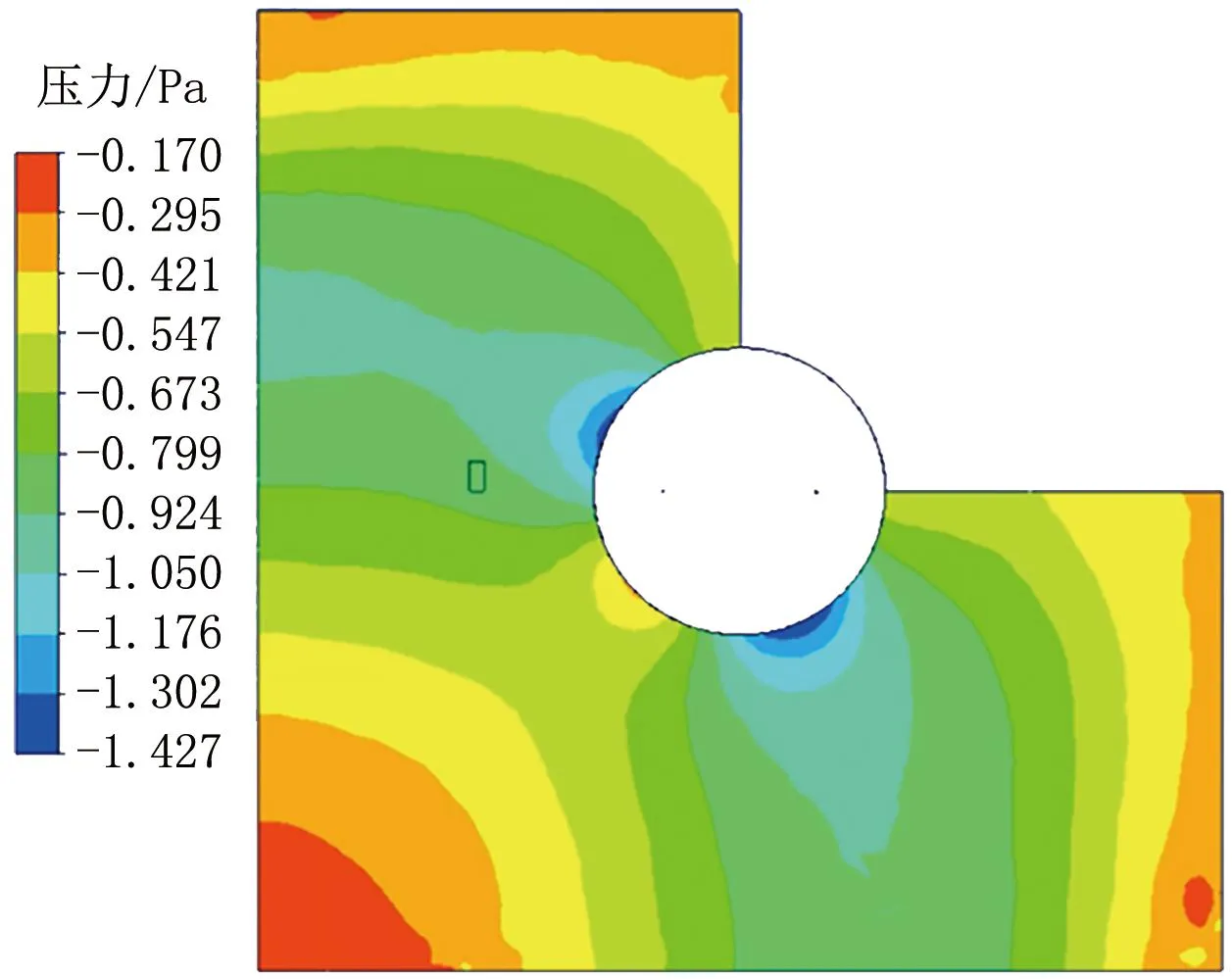
图16 234 s时平面1的压力分布云图

234 s时,平面1均为负压,压力基本为-1 Pa左右,分布较均匀。房间角落处存在高压区域,门缝处压力也较高,流动方向为从门缝向室内流动。平面1水蒸气质量分数基本维持在2.5%左右,门缝处由于有气流进入,水蒸气质量分数较小,存在浓度梯度。

平面2压力分布与水蒸气质量分数分布如图18、19所示。

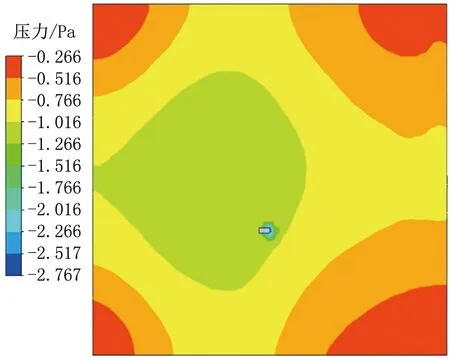
图18 234 s时平面2的压力分布云图

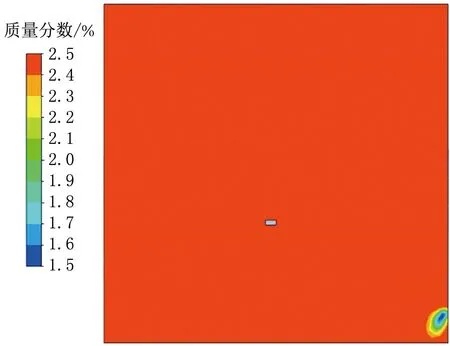
图19 234 s时平面2的水蒸气质量分数分布云图

234 s时,平面2压力均为负压且分布均匀,基本维持在-0.7 Pa左右,排风口附近压力较低,角落处存在循环死角,压力较高。水蒸气质量分数基本为2.5%左右,由于外部干净气流一直向室内输送,门缝附近水蒸气质量分数较小,为1.5%。

模拟计算的压力峰值与理论计算值有误差,但均在同一数量级,模拟气体运动过程与理论分析相符,仍可表示事故发生工况下泄漏物质扩散情况与室内压力分布。

3 结论

1) 得到了负压厂房气态物质泄漏后的理论计算方法。事故发生后,房间恢复负压所需时间取决于3个因素:排风量、泄漏水与空气的换热量、门缝面积。

2) 根据理论计算,事故后24 s时,室内压力达到峰值,为110.80 kPa,室内压力增大9.505 kPa。室内外压差恢复到0 Pa所需时间为390 s,恢复到-30 Pa所需时间为448 s。

3) 泄漏水与空气的换热量对室内压力峰值影响较大,泄漏水温度降低50%,室内压力峰值减小1.5%,恢复负压所需时间缩短7.1%;门缝面积对室内恢复负压所需时间影响较大,门缝面积增大到5倍时,室内压力峰值减小1.3%,恢复负压所需时间缩短78%。

4) 根据模拟计算,事故后24 s时,室内压力达到峰值,峰值为103.7 kPa,室内水蒸气质量分数平均为2.7%,平均压力为2.4 kPa;随着水蒸气由门缝向室外流动,234 s时,室内大部分区域水蒸气质量分数为2.0%,内部均为负压,基本为-1 Pa左右,室外空气由门缝向室内流动,室内水蒸气质量分数持续降低。室内存在气流死角,后续可通过优化排风口位置减少气流死角。

5) 事故发生后,由于大量水蒸气输入,室内压力快速上升,在24 s时达到峰值。后续由于室内持续排风,室内压力逐渐恢复至初始负压状态。模拟计算的压力峰值与理论计算值有误差,但均在同一数量级,模拟气体运动过程与理论分析相符,可显示事故发生工况下泄漏物质扩散情况与室内压力分布。