例谈高考物理中“变化趋势”类图像问题的解决策略
2024-01-25鲍习中
鲍习中
(池州市贵池区教育体育局教研室,安徽 池州 247000)
物理图像能直观地描述物理过程,形象地表达物理规律,鲜明地表示物理量之间的相互关系,是分析和解决物理问题的有效手段之一.在高中物理教学和各类考试中,物理图像问题无疑占有极其重要的地位,是高考命题的热点,它涵盖了各类题型,其中 “变化趋势”类图像问题又较为常见,此类题型的特点是:① 图像坐标系一般没有具体数值,只给出图像的大致样式和变化趋势;② 基本以选择题形式呈现,要求判断哪个图像最有可能正确.下面针对此类题型的基本解决策略以案说法,并进行梳理和总结.
例1.将一定质量的小球以大小为v0的初速度竖直向上抛出,不计空气阻力,则小球从抛出再到返回出发点的过程中,分别作出小球的速度-时间(v-t)、速度-位移(v-x)、动能-时间(Ek-t)、动能-位移(Ek-x)的图像如图1所示,其中可能正确的是
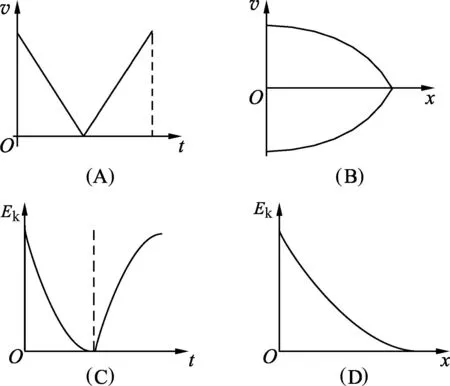
图1
1 求导法
求导法是解决“变化趋势”类图像问题的一种比较常用的快捷数学方法,导数的含义可理解为一个函数中因变量对自变量的变化率(也称之为斜率),下面针对该题阐述求导法的3种典型策略.
1.1 直接求导
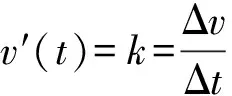
1.2 引元求导
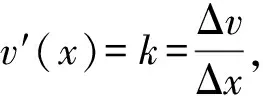
1.3 二次求导
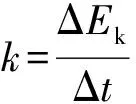
综上,可得正确选项为(B).
2 转换法
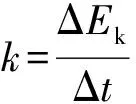
3 函数法
函数法是一种比较直接的解决方法,也是学生比较容易想到并使用的方法.思路为根据题目图像类型的要求运用相应的物理规律,写出对应的函数方程,然后借助数学知识判断图像的正确性.下面就从函数法的角度,对以上4个图像进行逐一分析.
(1)v-t图像.由于竖直上抛运动是匀变速直线运动,故由速度公式可得v=v0-gt,该函数为一次函数,其对应图线为直线,故正确图像如图2所示,(A)选项错误.
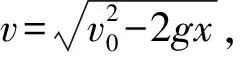
(3)Ek-t图像.由动能计算式可得Ek=
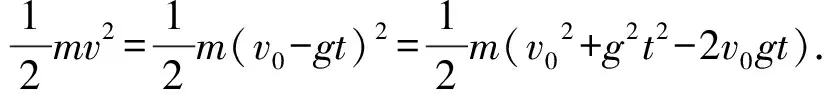
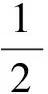
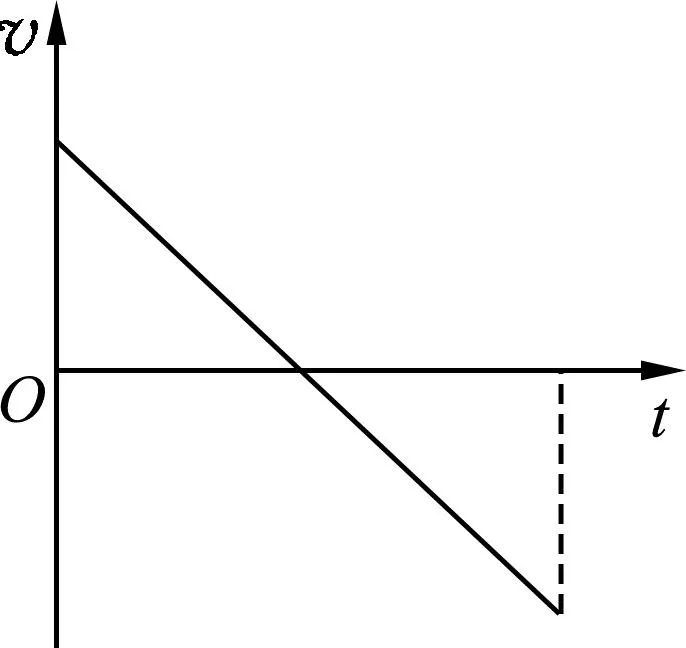
图2
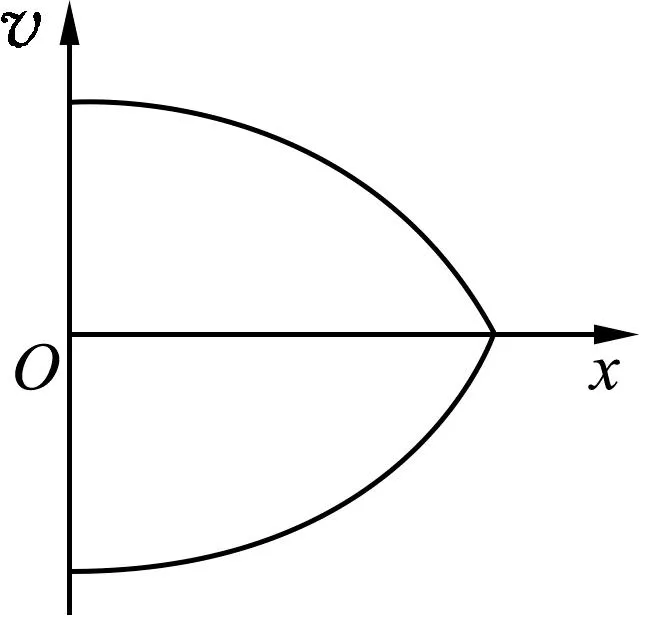
图3
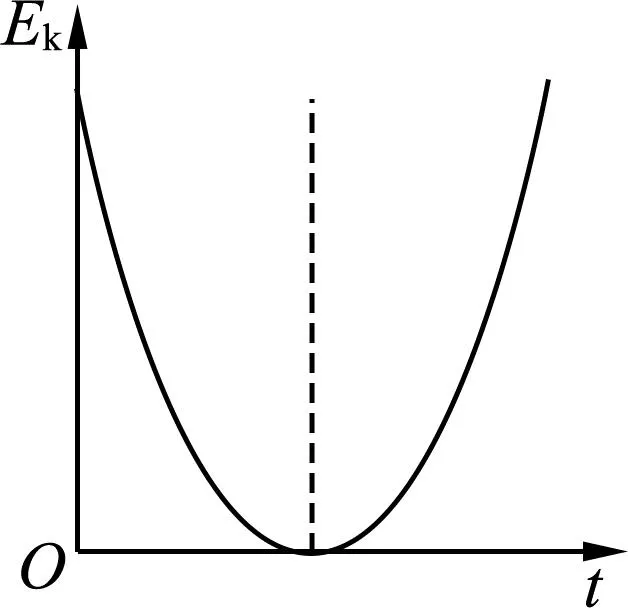
图4
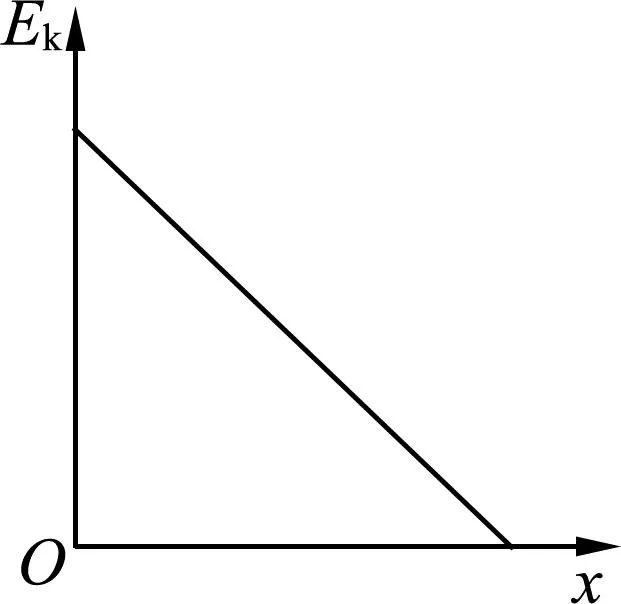
图5
4 应用示例
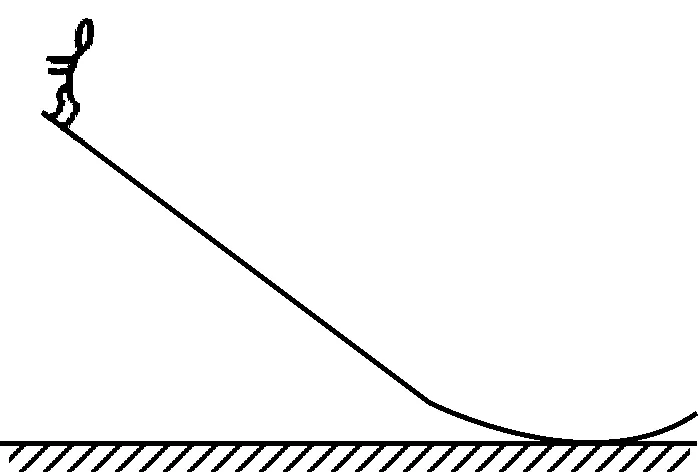
图6
例2.(2022年江苏省高考第8题)某滑雪赛道如图6所示,滑雪运动员从静止开始沿斜面下滑,经圆弧滑道起跳.将运动员视为质点,不计摩擦力及空气阻力,此过程中,运动员的动能Ek与水平位移x的关系图像(图7)正确的是
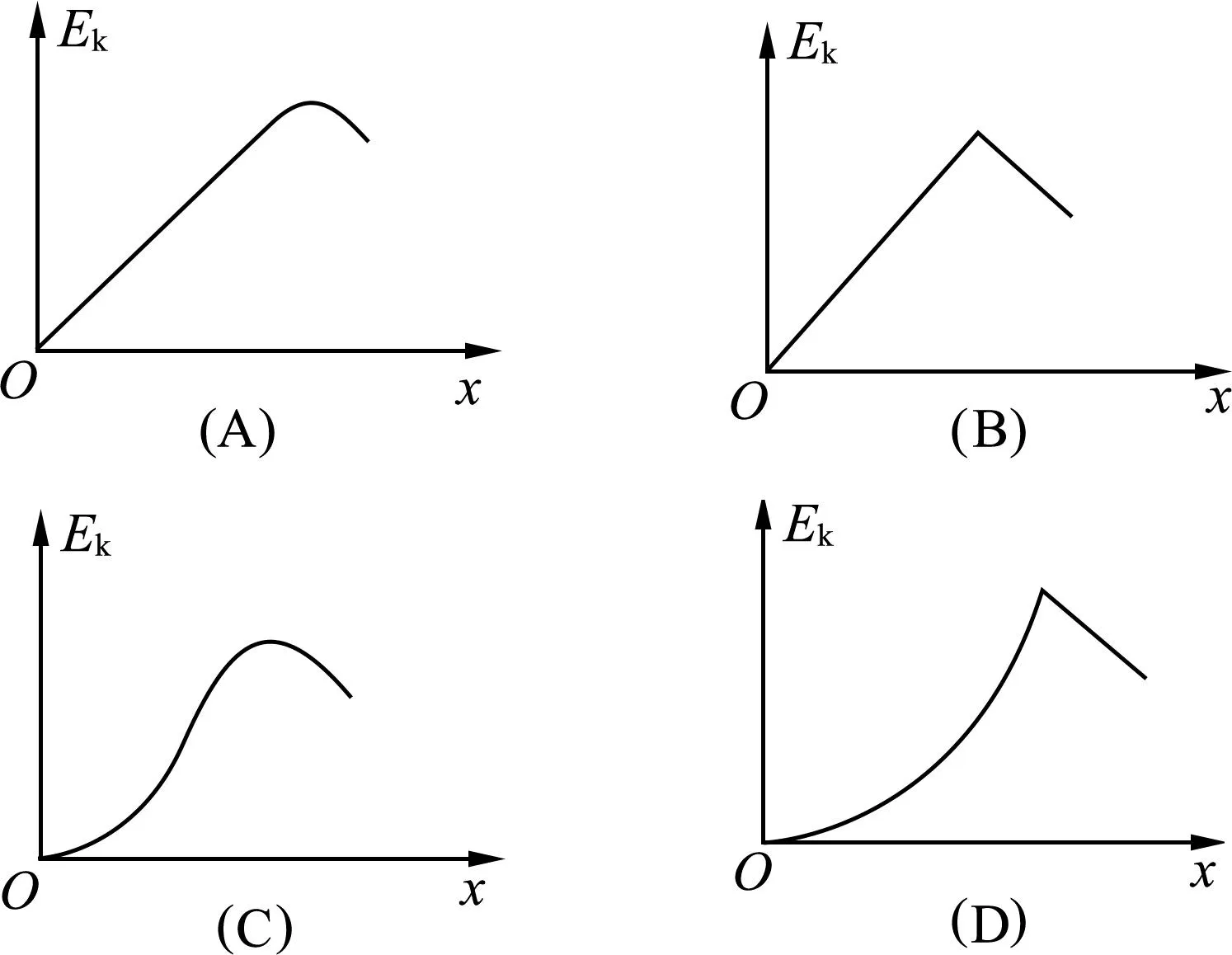
图7
由于本题中有一段曲线轨迹,没有明确的函数关系,只能考虑用求导法和转换法处理.
(1) 求导法.
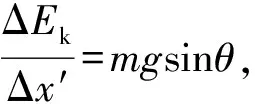
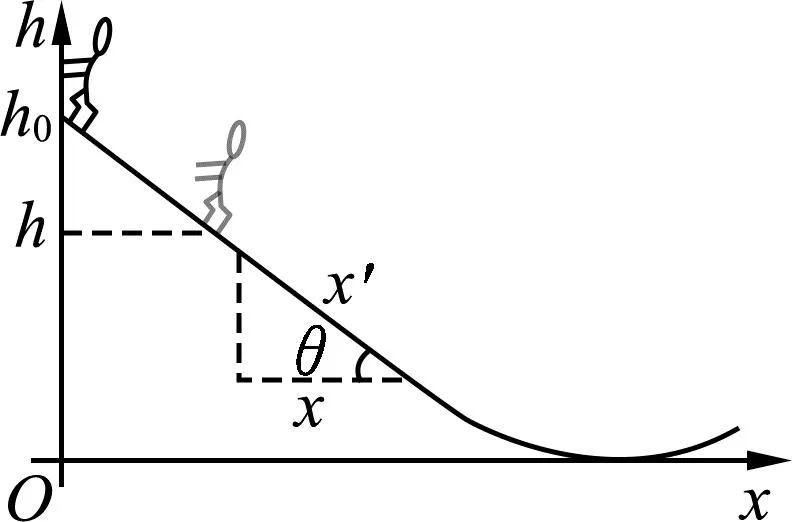
图8
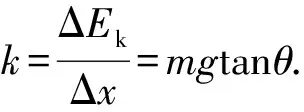
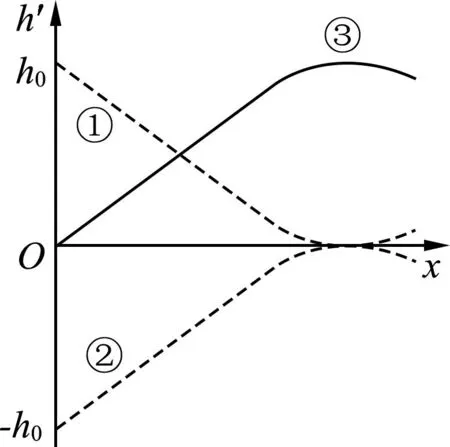
图9
(2) 转换法.
运动员运动的真实空间的轨道,其实本身就是一个h-x图像(h是运动员相对最低点的高度),如图9所示.本题相当于已知h-x图像,求解Ek-x图像.通过转化思想,将问题进一步简化,流程如图10所示及解析如下.

图10
转化1:由于初动能为0,故运动员的动能Ek就等于其相对初位置的动能的增量ΔEk,即Ek=ΔEk,则Ek-x图像可转化为ΔEk-x图像.
转化2:由动能定理可知动能的增量又等于重力做的功,即ΔEk=mgh′(h′为运动员下降的高度),则ΔEk-x图像可转化为mgh′-x图像.
转化3:由于本题只在于判断图像的变化趋势是否正确,故函数中的常数不会影响其图像样式和走势,则mgh′-x图像可略去mg简化为h′-x图像.
这样问题就被转化为已知运动员离地高度h随水平位移x变化的h-x图像,要求画出运动员下降的高度h′随水平位移x变化的h′-x图像,由空间几何关系不难得到这两个函数之间满足关系h′(x)=h0-h(x).而从h-x图像到h′-x图像,只需通过如图9所示的两步即可轻松完成,先将h-x的图线①关于x轴对称得到-h(x)的图线②,再将图线②向上平移h0即可得h′-x图线③.选项(A)正确.
