2023年江苏高考物理第10题赏析及教学启示
2024-01-25范伟
范 伟
(西南大学附属中学校,重庆 400700)
1 原题呈现及解法
例题.(2023年江苏高考物理第10题)达·芬奇的手稿中描述了这样一个实验:一个罐子在空中沿水平直线向右做匀加速运动,沿途连续漏出沙子.若不计空气阻力,则图1中能反映空中沙子排列的几何图形是
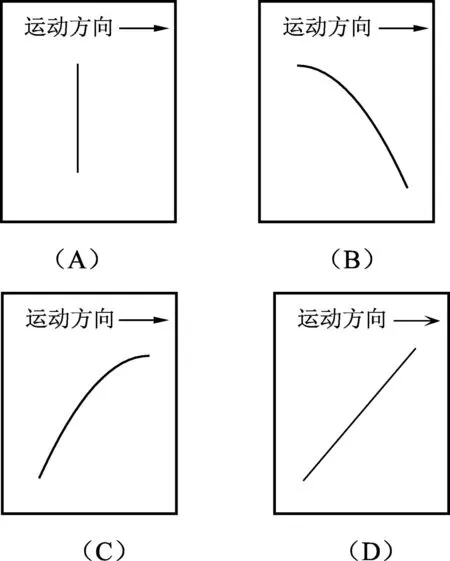
图1 高考物理题图
本题正确选项是(D),下面给出该题的4种解法.
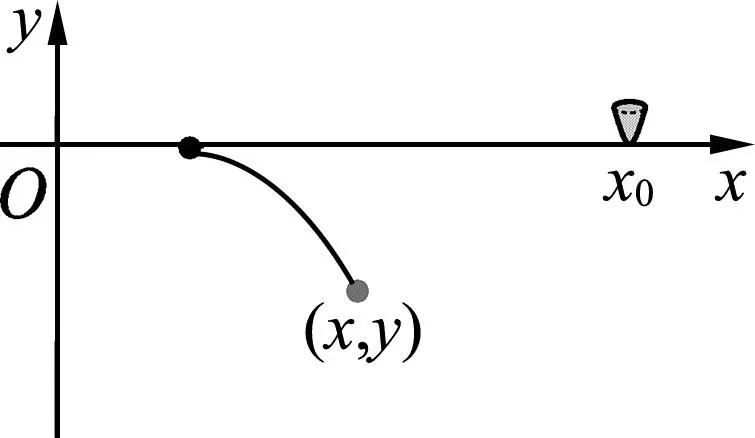
图2
方法1:令罐子在t= 0时刻速度为v0,加速度为a,t= 0时刻罐子位于坐标原点,在t0时刻位置坐标为(x0,0),如图2所示.
根据匀变速直线运动规律有
(1)
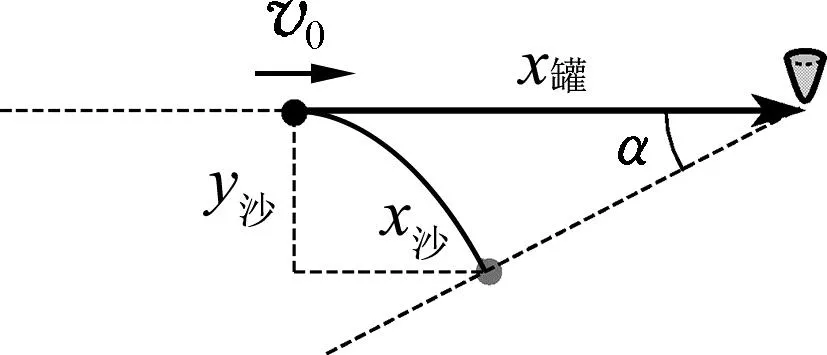
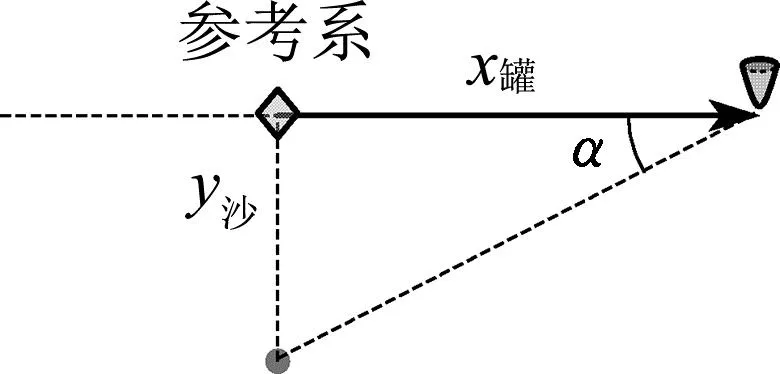
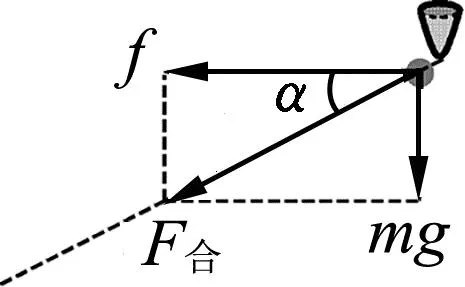
t(t (2) (3) 由式(2)(3)可得 (4) 即所有沙子排成一条斜率为g/a,纵截距为-gx0/a的直线. 方法2:令罐子的加速度为a,某粒沙子漏出时罐子的速度为v0,经过时间Δt,该粒沙子水平与竖直位移分别为 x沙=v0Δt. (5) (6) 罐子的位移为 (7) 如图3所示,罐子和该粒沙子连线与水平方向的夹角α满足 (8) 图3 可见夹角α与v0、Δt无关,即所有漏出的沙子与罐子连线在任意时刻与水平方向的夹角相等,所有沙子排成一条斜向左下方的直线. 方法3:令罐子的加速度为a,某粒沙子漏出时罐子的速度为v0.以相对地面做匀速直线运动(速度大小为v0,方向与罐子运动的方向相同)的物体为参考系,沙子和罐子的运动情况如下. 沙子在该参考系的正下方做自由落体运动,经过时间Δt,位移为 (9) 罐子做初速度为0的匀加速直线运动,经过时间Δt,位移为 (10) 如图4所示,罐子和沙子的连线与水平方向的夹角α满足 (11) 可见夹角α与Δt无关,即所有漏出的沙子与罐子连线在任意时刻与水平方向的夹角相等,所有沙子排成一条斜向左下方的直线. 图4 图5 方法4: 以罐子为参考系,当沙子漏出后受力情况为,水平向左的惯性力f=ma,竖直向下的重力mg,合力斜向左下方,大小为 (12) 如图5所示.沙子做初速度为0的匀加速直线运动,加速度大小为 (13) 方向斜向左下方.故所有沙子排成一条斜向左下方的直线,与水平方向的夹角α满足 (14) 题目以达·芬奇手稿中的内容为背景材料,有效地激发出了学生的好奇心,让学生关注这位艺术大师对科学的研究.手稿是指达·芬奇在1480年至1518年间留下的一份手稿——阿伦德尔手稿.[1]手稿是他本人各时期积累的短论文、笔记和图画,涉及到各个领域的奇思妙想.其中一页记载了一个跟重力加速度相关的思想实验:把装在罐子中的固体颗粒倒出,如果罐子以恒定的加速度加速运动,下落的颗粒就会形成一条笔直但倾斜的线,这时罐子运动的距离、颗粒组成的斜线、颗粒下落的竖直距离组成一个直角三角形,如图6所示.当罐子的加速度与重力加速度相等时,形成的三角形是等腰直角三角形.达·芬奇在等腰直角三角形旁边写下了一个古意大利语词组“equatione di Moti”,翻译过来大致是“运动的等效”.这表明达·芬奇通过引入一个水平的等值的加速度来研究重力加速度. 图6 课程标准指出,试题要“通过学生在应对复杂现实情境,参与相应探究学习活动中的外在表现来考查物理学科核心素养”.[2]本题正是通过罐子漏沙子这一真实情境考查了平抛运动、匀变速直线运动的知识.本题的情境对学生而言并不陌生,在学生日常的生活中也会遇到相似的情境.当然,达·芬奇手稿内容仅作为背景材料而存在,即使学生不知道达·芬奇的这一研究,也不影响学生对该试题的思考. 在高考语境下,一道好题,其标准之一就是具有良好的区分度,这样才能够把具有不同水平的学生区分出来.如前所述,此题的解答方法有多种,从创新性和数学运算繁简角度,不难看出此题不同的解答方法体现的思维水平不同.方法1采用的是常规方法,按照题目的要求写出沙子的位置坐标,从而判断出沙子排列的图形,但数学运算较为繁琐,耗时较长;方法2采用了由特殊到一般的推理过程,科学思维水平与方法一相比要高一些,数学运算较简单,耗时较少.方法3创新地提出以匀速直线运动的物体为参考系方式进行求解,科学思维水平更高,数学运算也更简单.方法4采用通过引入惯性力的做法,以最简数学运算(甚至是不需要运算)就可以得出答案.因此,科学思维水平越高的学生,在此题耗时越少,整张试卷获益(得分)也就越大,此题能有效地区分水平不同的学生. 此题无论采用哪种解法,都需要学生清晰地理解匀变速直线运动、牛顿第二定律、运动的合成与分解这些概念与规律.在教学中,教师要对促使学生理解概念与规律的工作狠抓不懈.只有这样,才能促进学生物理观念的形成,促进学生科学思维的发展,在解决物理问题时,才能找到最简洁的方法. 有研究表明,试题情境化会使难度增加.[3]面对情境化试题,考生需要先对情境进行分析、判断、简化、抽象,把情境化试题转化为非情境化试题然后再进行作答.因此在教学中,教师需要重视通过创设情境来建立物理概念,通过创设问题情境来探究物理规律,通过结合具体的实际情境来应用物理知识解决具体问题. 能够想到一题多解并能在考场上择优用之,需要考生具有高水平的质疑创新能力——这是科学思维构成要素之一.在问题解决的教学中,要加强审题训练,要让学生能够快速地从题干中发现隐蔽条件,能够排除多余因素,发现有价值的线索;要训练学生有意识地选择解题策略,确定解题方法;可以通过一题多变、一题多解、多题归一的方式,让学生归纳总结规律应用于解决问题的条件和步骤;要有意识地培养学生监控自己解决问题的过程,引导学生及时发现解决问题过程中遇到的困难,并能及时调整思维方向,修正原有的方案.[4]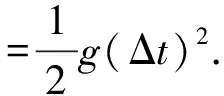
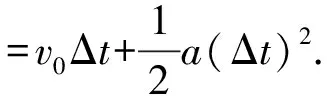
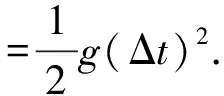
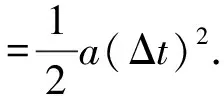
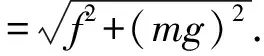
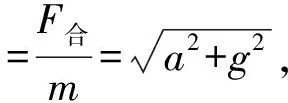
2 试题赏析
2.1 引导学生关注科学与艺术的统一

2.2 情境化命题思路,符合新课程标准理念
2.3 一题多解,巧妙地区分出不同水平的学生
3 教学启示
3.1 重视基本概念和规律的理解
3.2 重视创设物理情境
3.3 重视质疑创新能力的培养
