磁畴壁拓扑结构研究进展*

张颖 李卓霖 沈保根

(中国科学院物理研究所,磁学国家重点实验室,北京 100190)

1 引言

用数学上拓扑不变量的概念描述电子态、磁有序以及电荷分布等物理量,从而重新定义拓扑磁畴结构、拓扑铁电畴、拓扑绝缘体、拓扑半金属、拓扑超导体、拓扑光子晶体等拓扑物态和拓扑材料,极大拓展了对凝聚态物理和自然界的认识.理论上发现拓扑相变和拓扑相的工作在2016年获得了诺贝尔物理学奖,也充分说明拓扑在物理研究领域具有非常重要的科学意义.此外,拓扑非平庸的物态表现出许多新奇的拓扑量子现象,以及全局稳定性、低耗散、对光、电、磁等外场独特的响应等显著优点,因此如何调控拓扑物态、利用拓扑物性在拓扑磁性材料中开发全新的功能性量子器件具有巨大的应用前景.

数字化、智能化的信息时代,需要更低能耗、更高速度和更高密度的信息存储和处理载体,世界各国对新型磁性存储材料以及技术的发展极其重视.突破传统磁性信息存储技术面临的超顺磁物理极限、焦耳热、摩尔定律等应用瓶颈,实现新一代超高密度、超低功耗的新型自旋电子学器件,是极具前瞻性的重大基础科学问题和关键技术问题.在探索新型磁性信息材料和技术解决方案的过程中,研究人员发现以磁性斯格明子(skyrmions)为代表的磁矩空间排列具有拓扑性质的磁畴结构,亦即拓扑磁畴结构,其尺寸可至10 nm 量级,远低于现有的磁性信息存储单元的尺寸,可以大幅度提高磁性信息存储密度,而且其磁性状态能够被磁场、电流等多物理场有效调控,实现信息读写技术方法多样性,尤其特有的拓扑稳定性,有望成为新一代高密度、高速度、低能耗自旋电子器件的信息载体单元.

拓扑磁畴结构是一种具有局域手性自旋结构的特殊磁畴结构,是“对称性破缺理论”所描述的局域序参量的长程有序态,可以用拓扑数Q来描述[1]:,其中m是实空间(x,y)自旋单位矢量,Q描述自旋环绕单位球面的倍数,表现为不同的拓扑自旋组态,在凝聚态物理和材料科学中以磁性斯格明子为典型代表.当Q=±1 时自旋环绕单位球面完成一周,此时磁结构通常称为(反)斯格明子[2,3].斯格明子根据其磁矩旋转方式可分为奈耳Néel 型(平行径向)和布洛赫Bloch 型(垂直径向)[1].当Q=2 时为两个斯格明子的耦合,称为双斯格明子[4];当Q=1/2时,磁矩仅完成半周环绕,此时磁结构称为麦韧(meron)[5,6].图1 为典型拓扑磁畴结构的自旋分布示意图.拓扑磁畴结构拓扑数不随局域磁矩变化而改变,相应的拓扑物性对缺陷、微扰和细节不敏感,具有独特的全局稳定性,可实现能量和信息的无损传播.另一方面,从基础研究的角度,拓扑磁畴结构的生成和调控与Berry 相效应、拓扑霍尔效应、自旋转移力矩效应、自旋-轨道耦合效应等丰富的物理现象密切关联[7–9],从微观角度揭示拓扑磁畴结构的生成以及外场下的动力学行为,有助于深入理解奇异物理性能的微观机制,促进磁性新物态的探索和拓扑磁性器件的开发.

图1 常见的拓扑磁畴结构自旋分布图 (a)布洛赫型斯格明子[3];(b) Néel 型斯格明子[3];(c)反斯格明子[3];(d)双斯格明子[10];(e)麦韧[11]Fig.1.Schematics of typical topological domain structures: (a) Bloch-type skyrmions[3];(b) Néel-type skyrmions[3];(c) anti-skyrmions[3];(d) biskyrmions[10];(e) meron[11].

斯格明子的研究经历: 1962年英国粒子物理学家Skyrme[12]提出拓扑孤子概念,2006年Rößler等[13]首次理论预言其存在,2009年德国物理学家Mühlbaue 等[14]利用中子散射在手性单晶MnSi磁体中首次实验证实磁性斯格明子的存在.2010年,Yu 等[2]利用洛伦兹透射电子显微镜(L-TEM)首次实空间直接观察到磁性斯格明子稳定存在于FeCoSi 单晶中,解析的斯格明子拓扑自旋结构与模拟结果一致,极大地促进了拓扑磁畴结构的高分辨率解析以及原位外场调控研究.之后在拓扑磁性材料发现、物性研究、物态调控以及探索方面发展迅速,发现的新型拓扑磁畴结构如反斯格明子[3]、磁麦纫[5]、双斯格明子[15]、磁浮子等[16]可以由拓扑数进行统一表征.拓扑磁性材料体系也由最初的体Dzyaloshinskii-Moriya 相互作用(DMI)手性磁体(MnSi[14],Fe0.5Co0.5Si[2],FeGe[17]等)发展到界面DM 作用薄膜(Pt/Co/MgO[18],Pt/Co/Ta[19],Ir/Co/Pt[20]等)、中心对称偶极作用磁体(NiMnGa[21],La2–2xSr1+2xMn2O7(x=0.315)[15]等)以及Ruderman-Kittel-Kasuya-Yosida (RKKY)相互作用稀土磁 体(Gd2Pd Si3[22],Gd3Ru4Al12[23],TbMn6Sn6[24])等.不同材料体系中的斯格明子各具特点,但需要磁场稳定、温度低、密度低等不足无疑制约了相关器件的发展和应用.理论和实验已证实,电流驱动拓扑磁畴结构时受斯格明子霍尔效应[1,25,26](skyrmions Hall effect)的影响,拓扑磁畴结构会在侧向方向上发生偏转,甚至在样品边缘处湮灭,极大限制了其在自旋电子器件中的应用.图2 为斯格明子霍尔效应示意图以及实验观测结果.

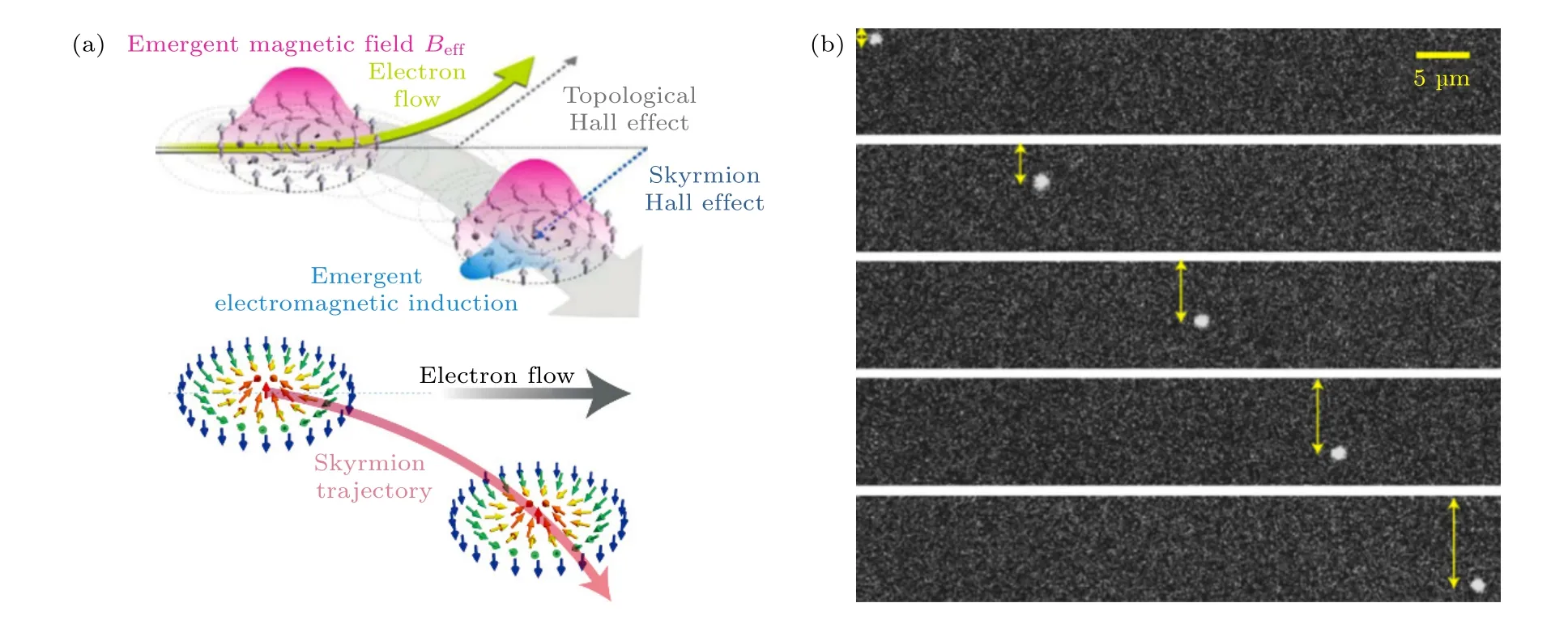
图2 (a)拓扑霍尔效应示意图[1,27];(b)实验结果[26]Fig.2.(a) Schematics of topological Hall effect[1,27];(b) experiment results[26].

上述不同材料体系中,虽然导致拓扑磁畴结构生成的主要磁相互作用机制不同,但我们发现各种磁相互作用竞争下产生长周期螺旋磁矩排列是形成拓扑磁畴结构的直接原因.利用磁学领域中面内磁矩与垂直磁矩过渡时的自旋重取向(spin reorientation transition,SRT)有利于倾角磁矩生成的特性,我们设计制备了系列Pt/Co/Ta 多层膜样品,通过增大铁磁Co 层的厚度使样品磁各向异性经历由垂直到面内磁矩SRT 转变,发现斯格明子密度逐渐增大的同时,其构型由Néel 型到Bloch型过渡[19],充分验证了自旋重取向生成斯格明子的机制.为了验证该机制的普适性,我们在多种稀土磁体材料中也发现了自旋重取向诱发生成的拓扑磁畴结构[24,28].除此之外,我们还注意到传统的180°磁畴壁具有天然的磁矩螺旋过渡区域,正好为半个周期的螺旋磁矩构型排布.虽然未见磁畴壁拓扑结构的实验研究,但2013年磁畴壁斯格明子的理论预测[29,30]为拓扑结构的研究提供了更多可能性.

2021年在二维范德瓦耳斯 Fe5–xGeTe2磁性材料中,研究了温度降低过程中垂直/面内磁矩自旋重取向引起的磁畴结构变化,实验发现无需磁场稳定的新型磁畴壁拓扑麦纫链,是由自旋重取向、天然螺旋磁矩排列的磁畴壁限域效应以及弱范德瓦耳斯力共同作用下由 180°磁畴壁自发演变形成,开辟了基于自旋重取向以及畴壁本征限域效应开展拓扑磁性物态探索和研究的新方向.在该研究思路指导下,进一步设计制备了不同成分的非晶亚铁磁 GdFeCo 薄膜,可以通过调节稀土元素和过渡金属元素的比例获得SRT 温度在室温附近的样品,温度变化过程中不仅再现零场磁畴壁麦纫态,还实现了磁畴壁拓扑麦纫态与磁畴壁斯格明子在自旋重取向附近的可逆演变,为研究新型畴壁拓扑态提供了更加便捷的材料体系.新型磁畴壁拓扑态和独特外场动力学行为在与当前微电子工艺兼容性高的二维材料及薄膜材料中的实验发现,有望实现未来自旋电子学信息技术的突破.

2 二维磁性材料Fe5–x GeTe2 中磁畴壁麦韧链的研究

近几年,二维范德瓦耳斯材料由于其新奇的物理特性和丰富的应用前景受到广泛关注[31,32].在单层或少层二维材料中发现的长程磁有序为二维材料在未来自旋电子学设备中的应用提供了更多的可能性,但CrI3[33],Cr2Ge2Te6[34]和VSe2[35]材料的居里温度(TC)较低,而FenGeTe2(n=3,4,5)系列二维材料[36–38]居里温度接近室温并且具有大的反常霍尔效应[39],Kondo 晶格[40]以及各向异性[37]等优异性能引起了极大的关注.在探索新型拓扑磁畴结构和材料体系的过程中,我们发现范德瓦耳斯二维磁体Fe5–xGeTe2在室温附近(TC～ 260—310 K)具有自旋重取向特征,磁性测量结果显示了ab面和c方向磁矩随温度的变化,进一步利用L-TEM 研究了二维磁体 (1¯10) 截面的磁畴随温度降低的演变行为,发现c方向连续的180°畴壁在自旋重取向附近演变为孤立的麦韧链(meron chain),如图3 所示.

图3 二维磁体Fe5–x GeTe2 畴壁中的麦韧链[11] (a) Fe5–x GeTe2 的晶体结构示意图,Fe(1)和Ge 位置被部分占据(用色差表示);(b),(e) 180 K 下两条畴壁对中选定区域的TIE 解析面内磁化分布(箭头和颜色分别表示平面内磁化的方向和强度);(c) 250 K 面内 180°畴壁的L-TEM 图像衬度(标尺为1 μm);(d)麦韧对在温度降低过程中的衬度演化;(f) 180°畴壁的三维内部磁矩排布示意图;(g),(h)两种手性(顺时针和逆时针)的麦韧结构Fig.3.Meron chains inside domain walls in 2D ferromagnets Fe5–x GeTe2[11]: (a) Crystal structures of Fe5–x GeTe2,and the positions of Fe(1) and Ge is partially occupied (labelled by color difference);(b),(e) the in-plane magnetization resolved by TIE in the selected regions of two domain walls at 180 K (arrow and color represents direction and amplitude of in-plane magnetization respectively);(c) the L-TEM contrast of in-plane 180° domain walls at 250 K (the scale is 1 μm);(d) evolution of meron pair contrast during cooling process;(f) 3D distribution of magnetization inside 180° domain walls;(g),(h) merons with two different chirality(clockwise and anti-clockwise).

二维材料Fe5–xGeTe2具有中心对称的R-3m空间群晶体结构(图3(a)),其中沿c轴堆叠的Fe-Ge-Te 层以较弱的层间范德瓦耳斯相互作用耦合.在Fe5–xGeTe2中,Fe(2)和Fe(3)位置被完全占据,但Fe(1)位置有明显的铁空位[38,41].室温附近Fe5–xGeTe2为c轴磁各向异性,磁畴结构以沿着c轴排列的传统180°磁畴为主(图3(c)).降温过程中自旋重取向作用下诱发了180°畴壁逐渐断裂,并在180 K 时形成完全的畴壁麦韧链(图3(d)),表现出小尺寸(≈ 20 nm)和高密度(≈ 24 μm–1)的特性.通过欠焦和过焦时磁畴壁衬度的变化进一步利用强度输运方程(transport of intensity equation,TIE)解析,在衬度明暗相反衬度的磁畴壁上分别得到逆时针和顺时针旋转排布的涡旋状面内磁矩构型(图3(b),(e)),颜色和箭头分别表示面内磁矩方向和相对大小,中间黑色区域代表中心磁矩朝向面外,而边缘磁矩朝c方向,与主体180°面内磁畴方向一致.因此,实空间解析获得的畴壁处由中间面外分布的磁矩到边缘面内磁矩过渡的涡旋型自旋结构,是典型的麦纫结构,其非线性磁矩周期为正弦螺旋型的一半,不同于整个正弦周期螺旋磁矩结构演变而来的斯格明子,因此其具有的拓扑数为–1/2[6,42].尽管根据L-TEM 的解析结果不能确定中心面外磁矩的绝对极性,但根据麦纫的定义,两处畴壁链的极性应该分别具有相同的朝内(麦纫)或朝外(反麦纫)的磁矩方向,在这里统一用麦纫对来表示.麦韧链的自发形成不需额外的磁场或DM 相互作用,是由于Bloch 型180°畴壁本身具有天然半周期螺旋自旋构型(图3(f)),同时受到垂直磁矩到面内磁矩过渡时的自旋重取向和c方向较弱的范德瓦耳斯力共同作用下的结果.逆时针和顺时针两种手性麦韧链成对出现,单一畴壁上的麦韧具有相同的手性和极性,符合中心对称Fe5–xGeTe2中的手性守恒(图3(g),(h)),此处只给出中心磁矩朝内方向的结果.畴壁麦韧链的稳定温度区间在230—130 K,温度继续降低时断开的麦韧链衬度进一步演变为连续的180°畴壁衬度.

进一步通过物理性能测量研究了各向异性变化与上述麦韧链形成过程的关联,沿Fe5–xGeTe2单晶两个不同方向(H//c和H//ab)的磁化率(χc(T)和χab(T))温度依赖曲线(图4)表明,沿c轴方向的χc(T)在居里温度TC附近突变,之后进一步降低温度呈现出较弱的温度依赖性(图4(a));而ab方向的χab(T)随温度变化明显,在温度约为258 K 处开始出现尖峰,该温度正好为畴壁麦韧链出现的温度点,同时尖峰顶端对应温度T≈ 180 K处与图3(d)中麦韧对完全分离稳定的温度点吻合.随着温度进一步降低至T<100 K,χab(T)曲线陡然下降,并与χc(T)数值相当,此时对应磁畴壁上的麦韧链消失.此外,两个方向测量的等温M-H曲线(图4(b))可以看出,275 K 时Mab(µ0H) 和Mc(µ0H)的饱和场大小µ0Hs基本相同,而在100—260 K 温区内,ab方向的饱和场小于c方向,说明磁矩排布逐渐由c方向逐渐转到ab面内,样品面内磁各向异性占主导,由于热扰动以及高温磁矩变弱,两个方向磁矩在磁滞回线上的差别表现并不显著,但自旋重取向转变过程中原位观察两个方向出现的磁畴结构清楚直观显示了自旋重取向转变过程,如图4(c)所示.温度低于100 K,两个方向的M-H曲线变化趋势相反且差异变得更加明显,此时c方向的饱和场变得更小,即易磁化轴变为c轴.综合上述测量结果可以确定降温过程中自旋重取向的转变与倾角的麦纫态出现有直接的关联,与之前的理论和实验研究结果一致[5,6].相比于手性磁体中需要DMI 以及外磁场辅助才能产生拓扑磁畴结构,中心对称二维范德瓦耳斯材料Fe5–xGeTe2中,通过降温自发形成的畴壁麦纫链结构将极大推进器件应用.

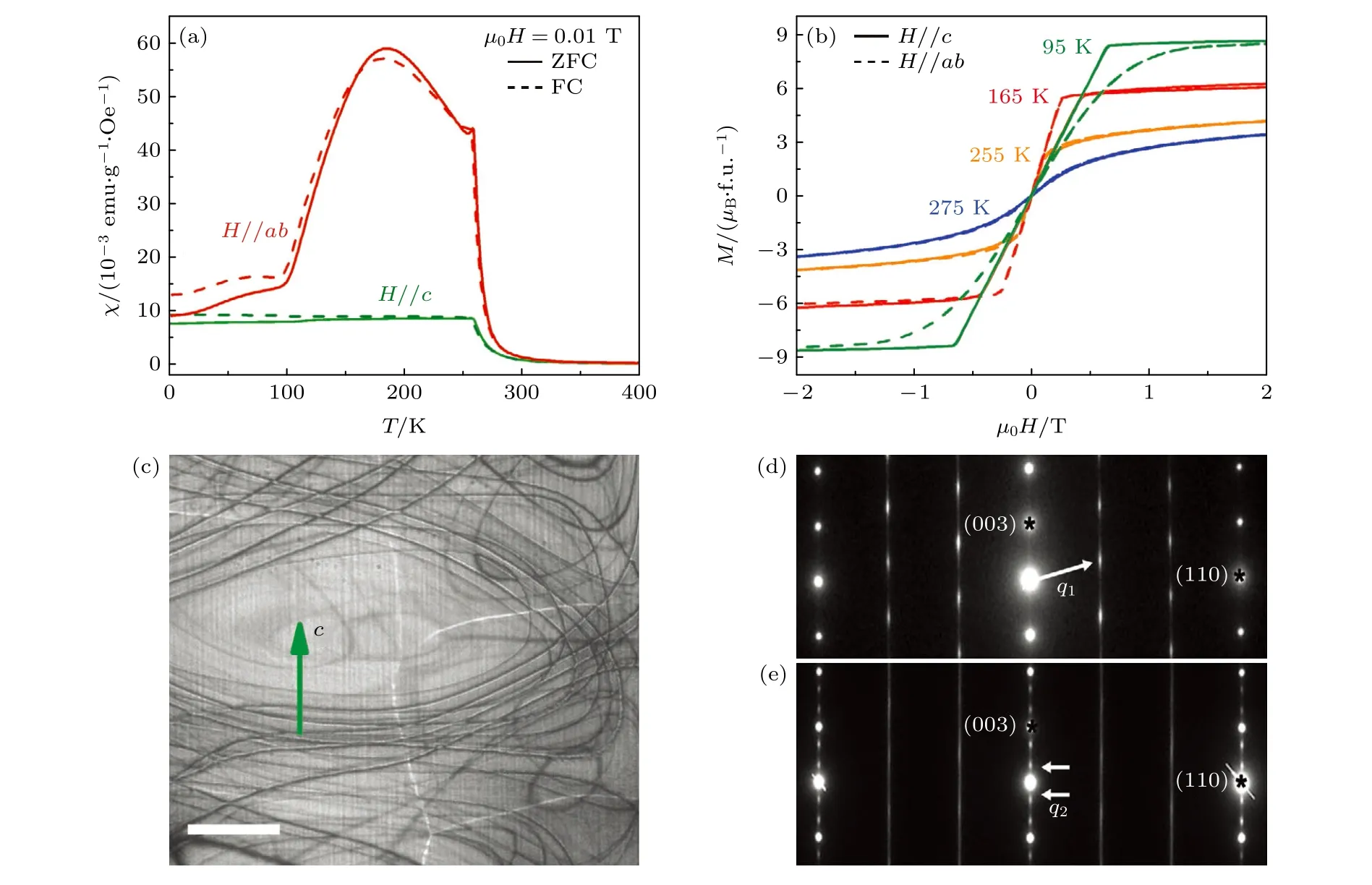
图4 Fe5–x GeTe2 中畴壁麦韧链生成的物理机制[11] (a)磁化率χ 在磁场沿两个方向(H//c 和H//ab)时的温度依赖曲线;(b)不同温度下磁场沿垂直方向和面内方向(H//c 和H//ab)的M-H 曲线;(c)自旋重取向区间存在的平行和垂直于c 轴的磁畴结构;(d),(e)温度高于100 K (d)和低于100 K (e)时,[110]晶带轴的选区电子衍射图Fig.4.Origin of domain wall meron chains in Fe5–x GeTe2[11]: (a) Temperature dependence of magnetic susceptibility χ as the magnetic field along two directions (H//c and H//ab);(b) M-H curve as magnetic fields along out-of-plane and in-plane direction (H//c and H//ab) at different temperature;(c) directions of domains parallel and perpendicular to c axis during SRT;(d),(e) SAED patterns of [110] ribbon axis at temperature above 100 K (d) and below 100 K (e).

变温过程中面内磁化率随温度的剧烈变化可能与Fe5–xGeTe2中Fe(1)位置的局部结构和磁性演化密切相关.图4(d),(e)分别为温度高于和低于100 K 时[110]晶带轴选区电子衍射(selected area electron diffraction,SAED)结果.温度在100 K以上时调制矢量为q1=± 1/3 (1,1,3)的电子衍射斑点和沿1/3 (1,1,l)方向的弥散衍射线出现.电子衍射调制结构主要是由较为无序的层内Fe(1)空位引入,最终导致了面内磁化分量的显著增强,此时c方向的原子有序调制结构还未形成.当温度低于100 K 时c方向额外出现的q2=±3/10 (0,0,31)调制结构电子衍射斑点揭示了该方向Fe 空位的长程有序,与100 K 附近的一级相变一致.Fe(1)位在层间空位有序导致磁矩沿c轴长程有序排列,此时c轴各向异性明显增强,最终导致了麦韧链的消失.这些实验结果表明,自旋重取向过程中磁矩的重排,沿c轴范德瓦耳斯弱相互作用以及畴壁本身独特的螺旋有序排列特征共同导致了畴壁(反)麦韧对的产生.相应的电学测试结果也表明Fe(1)亚晶格的有序排列不仅改变了磁各向异性还导致了电子自旋散射速率、电子结构和费米表面的剧烈变化.Fe5–xGeTe2中麦韧链的产生与其晶体结构、磁性和电子结构的变化之间存在很强的耦合关系.

进一步实验研究了沿c轴的畴壁麦韧链在电压和磁场等外场作用下的动力学行为.图5(a) 为对样品施加电压的示意图,探针接触样品后施加电压.图5(b)为从低温原位施加电压的视频中提取出的洛伦兹透射电子显微镜图.将样品降温至200 K 形成完全麦纫链后施加电压,电压加到5 V 时,观察到麦纫链对沿着垂直于电场方向的集体位移,之间的距离由开始的1.4 μm (图5(b))缩减为1.1 μm(图5(c)).麦韧链横向移动可能由电压作用在具有相同拓扑数的麦纫对上产生的马格努斯力导致,其表现出的集体运动与理论预测畴壁斯格明的行为一致[29,30].畴壁麦纫链的电学驱动行为展示了其与器件应用的兼容性,麦纫链受斯格明子霍尔效应影响下的集体运动行为也保证了信息的完整性.

沿c轴方向磁场的引入可以通过在施加垂直方向磁场的前提下倾斜样品实现.图5(d)为样品、c轴方向和外磁场三方相对夹角示意图(定义为α).垂直方向磁场通过增加透射电子显微镜的物镜电流施加,大小约为0.02 T,倾转样品引入磁场在样品面内的分量进而调控畴壁麦纫链之间的间距.图5(d)—(f)展示了倾斜角度增大过程中磁性麦韧链位置的显著变化,图5(g)定量记录了不同旋转倾角下两条麦韧链的相对位置.由图中可看出畴壁麦韧链的临界交换长度决定了其能稳定存在的最小相对距离,约为200 nm.在临界距离以上麦韧链的相对距离可以通过改变c方向的磁场大小来实现重复调节,而在该距离以下麦韧对发生耦合湮灭.磁畴壁拓扑磁畴结构随外场尤其与器件兼容性好的电压下的集体运动行为,可以保证信息的完整性,其临界交换长度对磁畴壁结构动力学进一步的理论计算和实验应用提供了研究基础.

3 非晶亚铁磁薄膜Gd FeCo 中磁畴壁拓扑磁畴结构的研究

现有电子器件的构建主要基于薄膜材料体系,在薄膜中研究拓扑磁畴结构更方便未来信息技术的集成和应用.薄膜体系具有制备便捷,表征手段丰富等优势,可以通过改变薄膜材料的制备条件、薄膜厚度、结构单元、重复周期等方法,更灵活地控制材料的磁性能参数、自旋重取向转变温区等特性从而调控拓扑磁畴结构的稳定区间、尺寸密度等特性.基于前期二维材料FeGeTe 中总结的磁矩自旋重取向,弱相互作用以及畴壁位置独特的螺旋自旋排列特征共同作用产生畴壁麦韧的机制,设计制备了系列具有自旋重取向的GdFeCo 非晶亚铁磁薄膜,拓展到器件集成技术更兼容的磁性薄膜体系.GdFeCo 具有垂直磁各向异性和较高的载流子噪声比,被广泛应用于热辅助磁记录(HAMR)、超快磁开关和逻辑存储器等领域[43–45].稀土元素和过渡金属元素两套磁矩子晶格组成的磁矩反平行排列,温度诱导的自旋重取向及可能的体 DMI 使得 GdFeCo 材料成为拓扑磁畴结构研究的热点,通过调节稀土元素Gd 和过渡金属元素FeCo 之间的相对比例,可以很方便地调控其垂直各向异性和自旋重取向温区.

磁控溅射过程中调节稀土和过渡金属之间的成分比例,生长了一系列具有不同自旋重取向温区的GdFeCo 非晶薄膜样品,样品厚度为 40 nm,利用L-TEM 进行了系统的磁畴结构研究,温度升高过程中样品的各向异性由面内向垂直方向转变,在各个样品的自旋重取向温区内都观测到了畴壁麦韧对与斯格明子之间的可逆转化.低于自旋重取向转变温度时,样品为面内磁各向异性,磁畴结构以面内畴为主,所以两畴分界处呈现出单色的电镜畴壁衬度 (黑或白),即180°畴壁衬度,利用强度输运方程解析,得到较强的面内磁矩分布(图6(f)),证实了样品在该温度下较强的面内各向异性[46].随着温度上升,样品的磁各向异性向面外方向转变,如图6(a)—(e) 所示[46].对图6(e)中畴壁两侧的磁畴结构进行相同条件下的磁结构解析,发现图6(j)中的面内磁矩分量相较于243 K 明显减弱,表明磁矩偏向面外方向.与传统180°磁畴壁不同,该样品的磁畴壁位置出现了成对的亚结构,分别为黑色圆形衬度以及白色条状衬度,如图6(a)所示[46].温度升高的过程中白色衬度逐渐消失.由强度输运方程解出的面内磁矩分量排布和变化表明磁畴壁亚结构磁矩的涡旋状排列方式以及磁矩在z方向上的连续性旋转,证实了麦纫对与斯格明子之间的转变.即在相互作用较弱的非晶薄膜中实现了磁畴壁麦韧链的生成,验证了前期在FeGeTe 中总结的实验规律和结论,并且利用自旋重取向转变,进一步实现了畴壁麦韧对与畴壁斯格明子不同拓扑态间的可逆转化,其他组分中出现了同样的现象,这表明该方法的普遍性和可靠性.

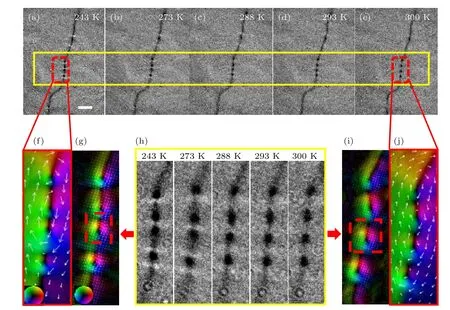
图6 随温度变化畴壁麦韧对与畴壁斯格明子之间转化[46] (a)—(e) 不同温度时,样品Gd15+x(Fe94Co6)85–x (x=0.2)在L-TEM下的磁畴壁衬度;(f),(g) 243 K 畴壁两侧和内部磁矩强度输运方程解析结果;(h) 图(a)—(e)中黄框部分放大;(i),(j) 300 K 畴壁两侧和内部磁矩强度输运方程解析结果(标尺为2 μm)Fig.6.Meron pair contrast change with temperature[46]: (a)–(e) Evolution of domain wall L-TEM contrast with temperature in Gd15+x(Fe94Co6)85–x (x=0.2);(f),(g) TIE results inside and outside domain walls at 243 K;(h) enlarged part of yellow box in panels (a)–(e);(i),(j) TIE results inside and outside domain walls at 300 K (The scale bar is 2 μm).

利用OOMMF 软件进行微磁学数值模拟计算,进一步总结了畴壁处拓扑磁畴结构转变的规律.首先利用实验测得的M-H曲线提取出自旋重取向转变温区附近的饱和磁化强度Ms和垂直各向异性常数Ku(图7(a))[46].此处讨论的Ku为薄膜在制备工艺过程中引入的本征垂直各向异性常数,不包含退磁能的影响,故其数值始终大于零.以麦韧对为初始态,研究不同Ku和Ms下涡旋状麦韧的拓扑数(Ns)变化,得到了如图7(b)所示的相图,其中颜色越深的部分代表磁畴结构的拓扑数越高[46].图7(a) 中4 个温度对应的实验Ms和Ku值刚好位于相图中麦韧向斯格明子转变的区域(图7(b)的红色菱形标志).说明磁畴壁处拓扑结构的转变是由自旋重取向转变过程中垂直各向异性和饱和磁化强度变化共同决定的,微磁学模拟相对应的270—300 K 麦韧对(图7(d))到斯格明子(图7(g))的磁结构演化可以清楚表明拓扑数由麦纫态–0.5到斯格明子1 的变化过程,并且磁性麦纫态和斯格明子态的洛伦兹图像衬度的模拟结果也与实验结果一致(图7(c),(h))[46].

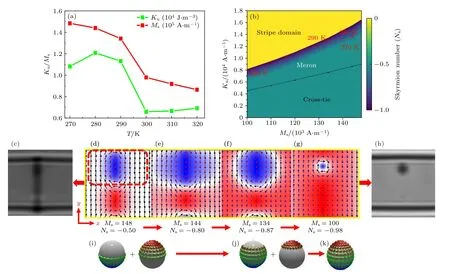
图7 磁性参数变化决定的磁畴壁拓扑结构演变及微磁学模拟结果[46] (a) Gd15+x(Fe96Co6)85–x (x=0.2)样品不同温度下的单轴各向异性常数Ku 和饱和磁化强度Ms 实验数据;(b)不同Ku 和Ms 下麦韧对拓扑数演化结果相图及实验中自旋重取向转变温区所在区域;(c),(h) L-TEM 衬度模拟结果;(d)—(g) 270—300 K 麦韧对到斯格明子的模拟畴壁演化,面外磁化由红色(+mz)和蓝色(–mz)表示,面内磁化由白色区域和黑色箭头表示;(i)—(k)对应的自旋结构示意图立体投影Fig.7.Micromagnetic simulation results of domain wall topological transition[46]: (a) Experimental data of anisotropy constant Ku and saturation magnetization Ms at different temperature in Gd15+x(Fe96Co6)85–x (x=0.2);(b) the phase diagram of topological transition starting from meron pair at different Ku and Ms value and the SRT regions observed in experiment;(c),(h) simulation results of corresponding L-TEM contrast;(d)–(g) evolution from meron pairs to skyrmions by simulation at 270–300 K,the out-ofplane magnetization is indicated by red (+mz) and blue (–mz),the in-plane magnetization is indicated by white region and black arrows;(i)–(k) 3D schematics of corresponding spin structures.

不同品质因子Fq下磁畴壁的系统演变模拟结果如图8 所示,其中,Fq为垂直各向异性和饱和磁化强度影响的形状各向异性的相对大小.可以看到在Fq=1 的两侧,两者能量上分别占据主导地位,对应面内和垂直两个方向自旋重取向转变的整个过程,图7(a)中实验测量的Ku和Ms值对应Fq值及磁畴结构演变被重点标出,在Fq趋近于1 时,磁矩更易处于倾角的状态,有利于斯格明子的稳定[47].当Fq值大于1 时自旋重取向到垂直磁各向异性,磁矩主要沿垂直方向排列,磁畴壁结构消失,垂直方向的传统磁畴出现,拓扑数为0.

图8 不同Fq 值下畴壁拓扑结构演化的微磁学模拟结果[46]Fig.8.Simulated topological domain evolution in domain wall for different value of Fq[46].

进一步对磁畴壁拓扑结构形成机制进行分析,我们认为低温下畴壁麦韧对的稳定和形成与畴壁中的布洛赫线(Bloch line)有关.在缺乏DMI 的材料体系中,同一条畴壁上的手性不一致会导致布洛赫线的产生.布洛赫线的间距由材料本身的参数决定,该薄膜体系中高密度的布洛赫线将面内的布洛赫畴壁切割,分割的部分组成一列麦韧和反麦韧亚结构,如图9 所示.麦韧的尺寸由布洛赫线间距和畴壁的宽度决定,以270 K 的Ms和Ku的值为初始值,以随机态为初始态的微磁学模拟结果如图9(b),(e)所示,磁畴壁内部极性相反的麦韧对结构会自然交替出现,且麦韧的尺寸固定,与实验及理论分析结果一致.

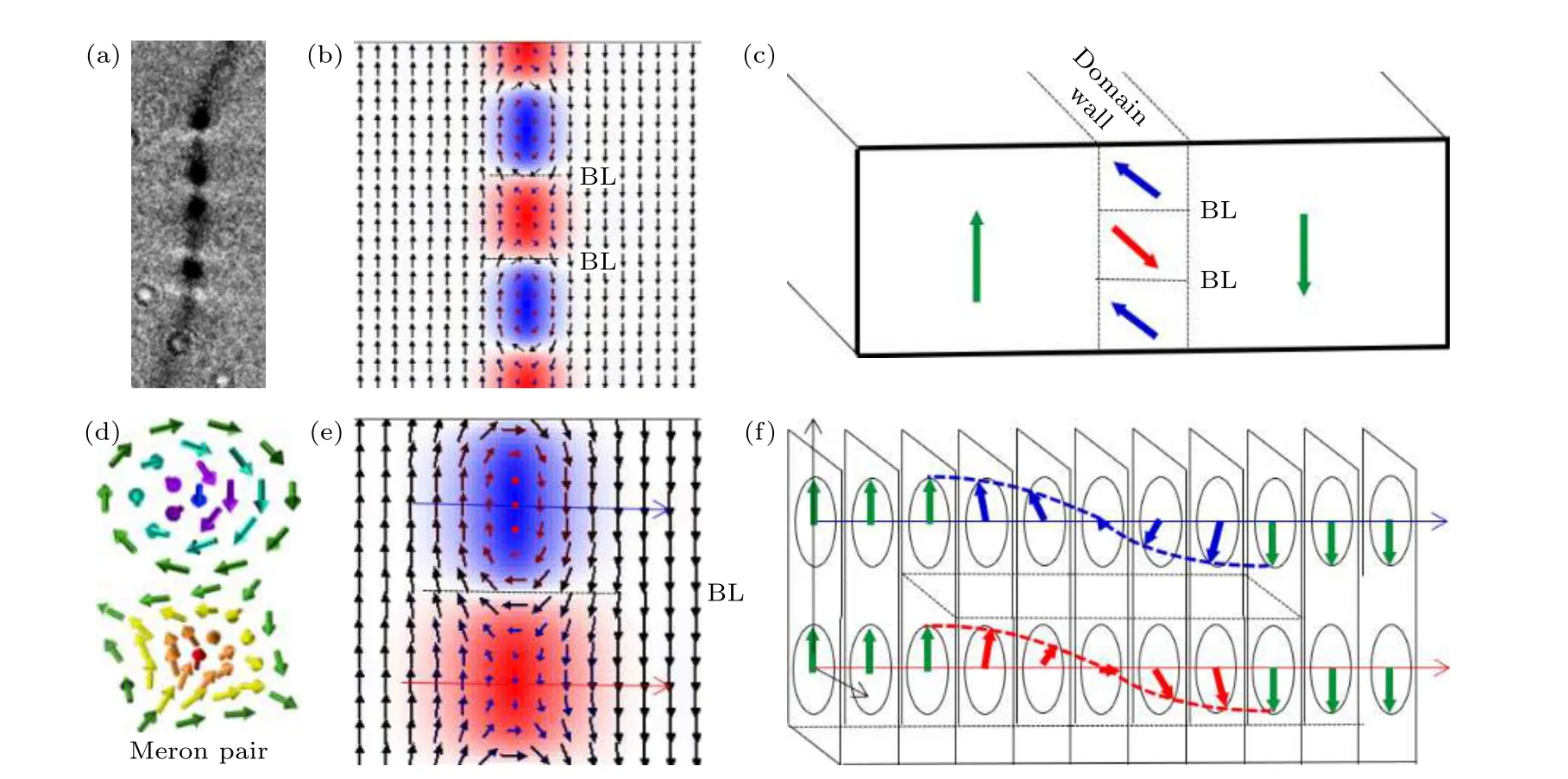
图9 畴壁麦韧链结构及生成机理示意图[46]Fig.9.Schematics of domain meron pair and its forming mechanism[46].

磁畴壁拓扑磁畴结构在电流下的动力学行为有望克服斯格明子霍尔效应引起的偏转.在OOMMF利用带有绝热和非绝热自旋转移力矩项的LLG 方程[48]构建微磁学模拟模型:

式中,γ0为旋磁比常数;H代表微磁学中总的有效场,包括外部磁场、交换作用场、各向异性场等;m单位矢量表示局部磁化强度;α 和β 分别是Gilbert 阻尼因子和非绝热系数;u定义为电子的速度矢量.u的幅值与电流密度J和极化P的大小成正比,其对应的换算关系为

其中,Ms=1 × 105A/m,A=7 pJ/m,P=0.4,阻尼系数α=0.1,β=0.04.电子极化率极化P、阻尼系数α 和非绝热自旋转移力矩系数β 选取OOMMF 求解器中默认数值.图10 为微磁学模拟结果,在电流密度为1011A/m2,对应电子速度为100 m/s 的恒定电流影响下,斯格明子受STT 驱动沿磁畴壁运动,侧向偏转角度仅为0.03°,说明畴壁的限制作用有效地克服了斯格明子霍尔效应,有望应用在磁性信息器件.

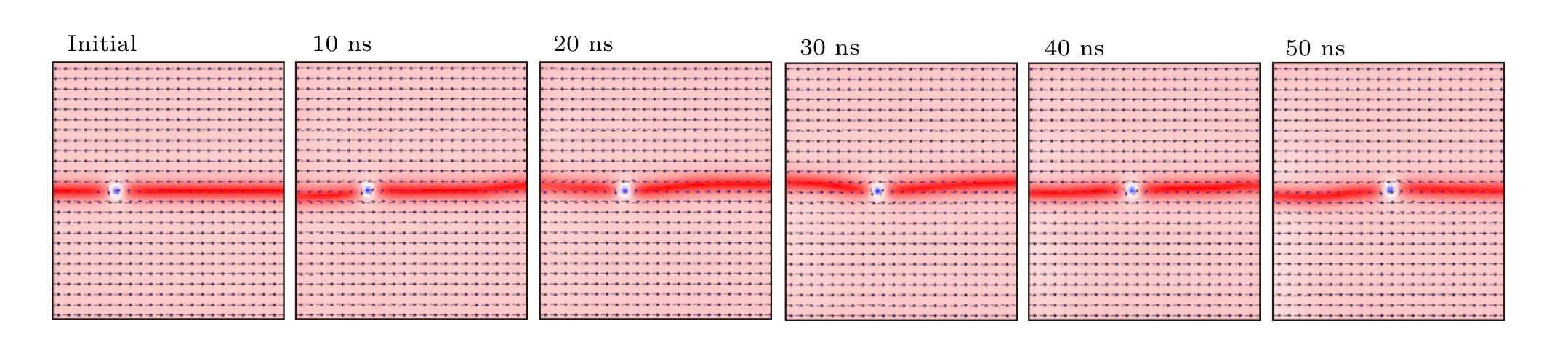
图10 微磁学模拟下电流驱动下畴壁斯格明子随时间的位移[46]Fig.10.Simulated drift of domain wall skyrmions with time under applied current[46].

为验证理论模拟结果,在实验中施加32 mA直流电,首次观测到畴壁斯格明子在电流作用下沿着畴壁方向蠕动,并在电流关闭后能被明显观察到与初始态的相对位移,即图11 中红色、黄色和绿色圆框分别标注的畴壁上3 个斯格明子在不同时间段的位置变化.但由于样品中缺陷等因素对磁畴结构的钉扎效应,我们并未观察到微磁学模拟中的斯格明子连续长距离的移动.如果进一步增大电流幅值,就会实现了STT 诱导的自旋重取向转变.因此,如何设计材料和器件从而有效克服钉扎效应实现斯格明子沿磁畴壁的信息传输是下一步要解决的重要问题.

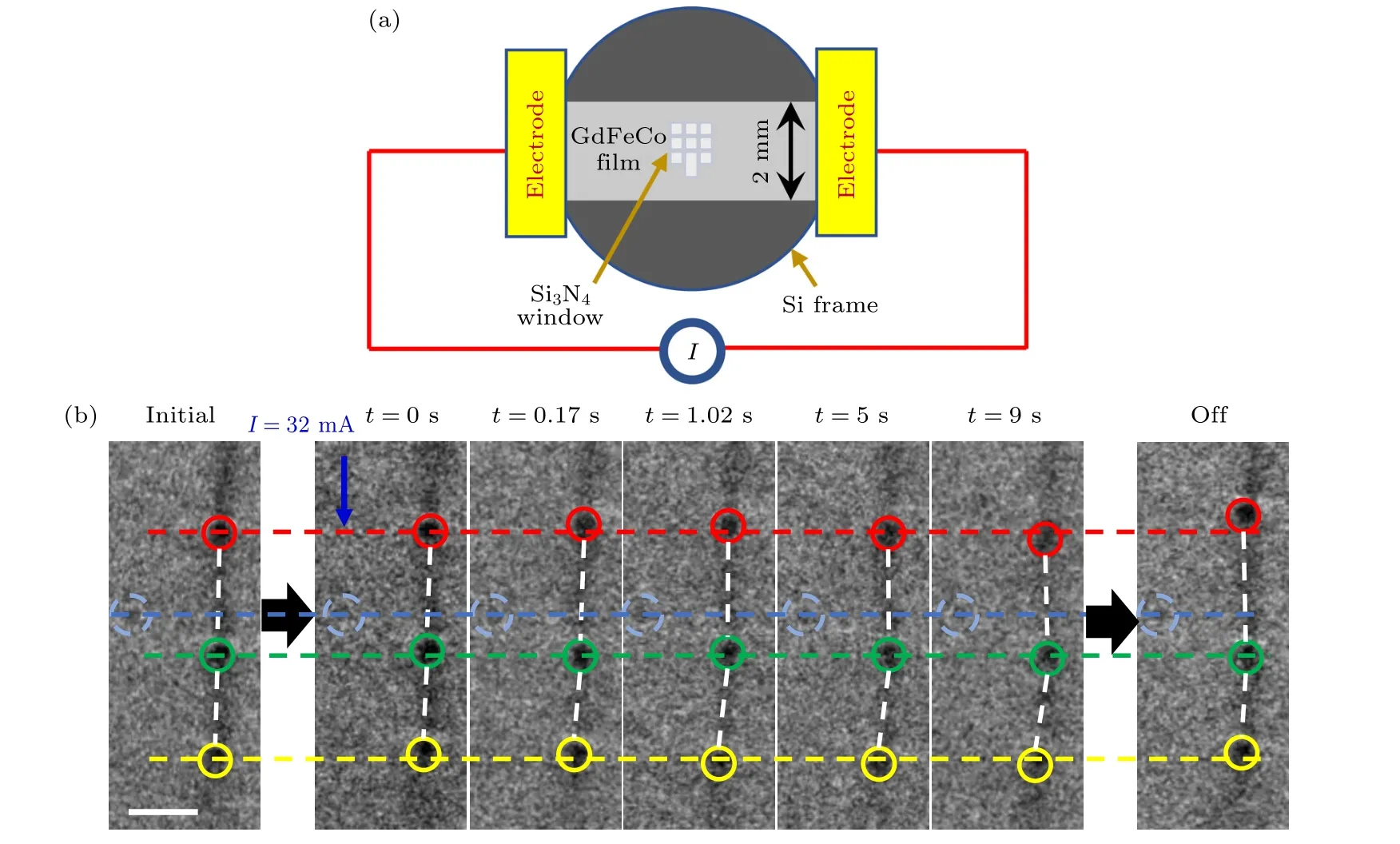
图11 电流调控实验结果[46] (a)原位电流实验示意图;(b)畴壁斯格明子在32 mA 直流下不同时间点的位置变化(标尺为500 nm)Fig.11.Experimental results under electric stimulus[46]: (a) Schematics of in-situ current experiments;(b) position change of domain wall skyrmions at different time under 32 mA DC (The scale bar is 500 nm).

4 总结与展望

利用洛伦兹透射电子显微技术及多场辅助调控,系统研究了二维材料中磁畴壁处拓扑磁畴结构的生成和转化,并利用磁性测量、微磁学模拟等手段对其物理机理进行了深入探讨.在范德瓦耳斯中心对称二维磁体Fe5–xGeTe2中,通过降温诱发自旋重取向,实现了零场下180°磁畴壁到(反)麦韧链的转变,揭示了一种新颖的磁畴壁限域效应生成新型拓扑磁畴结构的机制.依据自旋重取向、弱相互作用和磁畴壁限制对畴壁拓扑结构的关键机制,设计制备非晶亚铁磁GdFeCo 薄膜,实现了畴壁麦韧对的可控生成以及与斯格明子之间的拓扑转变,为基于磁畴壁限制作用以及天然磁畴壁螺旋磁矩排列生成畴壁拓扑结构提供了重要实验及理论依据,在自旋电子学及存储领域具有潜在的应用价值.理论提出磁畴壁斯格子数年之后[31],新型磁畴壁拓扑态在与当前微电子工艺兼容性高的二维材料中的实验发现,有望实现未来自旋电子学信息技术的突破.磁畴壁特有的外场调控下集体行为的实验研究,对畴壁内拓扑结构动力学的理解及其在电子学、自旋电子学存储中的应用创造了更多机遇.