基于泵浦强度调制的超快光纤激光器中孤子分子光谱脉动动力学研究*

方振 余游 赵秋烨 张昱冬 王治强 张祖兴‡

1) (南京邮电大学电子与光学工程学院,柔性电子(未来技术)学院,南京 210023)

2) (安徽大学,信息材料与智能感知安徽省实验室,光电信息获取与控制教育部重点实验室,合肥 230601)

1 引言

超快激光器中孤子分子是由两个或多个孤子间相互作用形成的一种束缚态结构,其形成来源于腔内非线性和色散效应、增益和损耗等物理因素引起的孤子间的排斥力和吸引力之间的平衡[1,2].孤子分子是超快激光器中的一种固有结构,其内部蕴含着丰富的非线性动力学,例如相位或间距变化的孤子分子[3]、谐波锁模孤子分子[4]以及孤子分子复合物[5]等.深入研究孤子分子对于理解孤子间复杂非线性动力学以及超快激光器内在物理机制具有重要意义.

色散傅里叶变换技术(dispersion Fourier transform,DFT)是一种实时光谱测量技术,原理是利用不同频率的光在色散介质中传播速度不同,将入射脉冲在色散介质中展宽,当远场出射端满足一定色散条件时,在时域上实现对入射场光谱强度分布的实时测量[6–8].DFT 在超快光学中的引入极大地推动了超快孤子非线性动力学领域的研究,揭示了丰富的孤子瞬态动力学,例如孤子爆炸[9]、孤子分子形成[10]、孤子分子共振[11]和混沌孤子[12]等.

区别于传统孤子,孤子分子的表征具有两个额外的自由度: 孤子间距以及孤子间相对相位.这二者取决于孤子间的相互作用强弱,孤子分子表现出孤子间距振荡型、相位振荡型或滑动型等丰富的动力学行为[13,14].通过对腔内泵浦功率、色散、光场相位等调控,一定程度上实现了对孤子分子间距和相位的操控[10,15].前期报道中观察到了泵浦调制引起的脉冲周期性振荡和光谱中心波长振荡[16–18].然而,针对脉动孤子分子的操控及相关动力学的研究尚属空白.

本文报道了基于泵浦强度调制的超快掺饵光纤锁模激光器中光谱脉动的孤子分子动力学,采用DFT 技术重点研究了光谱脉动孤子分子间距及孤子间相对相位对调制频率的响应,实现了不同内部动力学脉动分子之间的调控.研究成果对孤子分子在未来大容量光通信传输以及大容量全光存储等应用方面具有重要的指导意义.

2 实验装置

实验装置如图1 所示.光纤激光器由976 nm半导体激光器(LD)、信号发生器(SG,RIGOL,DG1022 U)、波分复用器(WDM)、掺铒光纤(EDF)、10/90 光耦合器(OC)、可饱和吸收镜(SESAM)和一个偏振控制器(PC)组成.其中LD输出功率、波形等特性由SG 控制,PC 用于改变腔内偏振态,通过SESAM 饱和吸收产生锁模脉冲.EDF 长0.7 m,在1550 nm 处色散为61.5 ps2/km,其余为单模光纤(SMF-28 E),在1550 nm 处色散为–22.8 ps2/km,全腔长为14.47 m,重复频率为14.65 MHz,腔内净色散约为–0.267 ps2.输出脉冲最后由50∶50 OC 分为两束光: 一束由光谱分析仪(OSA,YOKOGAEA,AQ6370D)进行光谱测量;另一束经过8 km 的色散补偿光纤(DCF)进行展宽,展宽后的时域脉冲信号经33 GHz 高速光电探测器(PD,Keysight)转换为电信号,接到带宽为33G示波器(OSC,Keysight Infiniium V,DSAV334A)记录实时光谱,其中DCF 在1550 nm 的色散为56 ps2/km.因此,DFT 对应的光谱分辨率为0.098 nm,时间分辨率为5 ps.

图1 实验装置图.SESAM,可饱和吸收镜;SG,信号发生器;LD,半导体光源;WDM,波分复用器;EDF,掺饵光纤;PC,偏振控制器;OC,90∶10 耦合器;DCF,色散补偿光纤;OSA,光谱分析仪;OSC,实时示波器Fig.1.Diagram of experimental setup.SESAM,saturable absorber;SG,signal generator;LD,semiconductor light source,WDM,wavelength division multiplexer;EDF,erbium-doped fiber;PC,polarization controller;OC,90∶10 coupler;DCF,dispersion compensation fiber;OSA,optical spectrum analyzer;OSC,oscilloscope.

3 实验结果及分析

图2 对比了不同调制频率情况下,泵浦激光器发出的泵浦波形和信号发生器输出的载波信号.调制信号采用矩形,高电平为1.53 V,低电平1.50 V,占空比为50%,调制深度设为2%,如图2(a)虚线波形所示.为了更好地展示光功率的实时变化,泵浦激光器输出的激光经光电转换器转换为电信号,接入示波器进行检测.图2(a)实线波形为调制后的泵浦激光器输出信号,由于PD 的功率限制,该波形是经过10∶90 耦合器后示波器的检测结果.实际最大功率为53.63 mW,最小泵浦功率为47.78 mW,调制深度为12%.从图2(a)可以看出,泵浦激光器输出的功率大小可以由调制信号进行调控,其功率变化的周期、幅度等均可通过改变调制器的调制频率、调制深度等进行控制.图2(b)给出了不同电压下泵浦激光器的输出功率.值得注意的是,在不同驱动电压情况下,即泵浦激光器上的驱动电压从1.5 V 上升至1.53 V 的区间内,激光器均能实现良好的锁模,观察到稳定的孤子分子输出,且无需对腔内任何条件进行改动.因此,后续实验仅在驱动电压从1.5 V 至1.53 V 区间内研究了激光器腔内的孤子分子动力学.

图2 (a) 输入泵浦脉冲波形(实线)和载波信号波形(虚线);(b) 调制电平和泵浦功率关系图Fig.2.(a) Input pump pulse waveform (solid line) and carrier signal waveform (dashed line);(b) modulation level and pump power relationship diagram.

当泵浦调制频率为1 kHz,得到了稳定的孤子分子,结果如图3 所示.孤子分子的实时光谱如图3(a)所示,可以观察到光谱周期性地发生红移和蓝移,这种现象被称为孤子分子光谱脉动.通过对脉动光谱的分析可知,光谱脉动的幅度为1.2 nm,脉动周期为1 ms,与调制信号的频率相对应 (1 ms),证实了光谱变化是由泵浦功率导致.通过对DFT 单次光谱进行傅里叶变化可得到其一阶光学自相关(AC).从图3(b)的自相关轨迹演化可以看出,脉冲间距保持不变,表明孤子间的间距受泵浦强度的影响较小.图3(c)给出了孤子分子总的能量随圈数的演化,清楚地表明了孤子分子光谱脉动与腔内功率即非线性强弱有关.当腔内能量较低时,孤子分子光谱发生红移;反之,腔内能量较高时,光谱发生红移,如图3(d)所示.图3(e)给出了两种典型情况下DFT 光谱的对比.这种现象可理解为增益诱导的孤子分子光谱脉动[17].在调制信号引起泵浦功率变化时,由于EDF 中Er3+集居反转数的变化使EDF 增益谱重塑,从而导致波长发生周期性红移或蓝移.然而,当腔内能量稳定时,孤子分子光谱缓慢地蓝移或红移,这一方面是因为泵浦功率随驱动电压大小响应的非线性导致,另一方面可能与超快激光器迟滞效应有关[5,13].

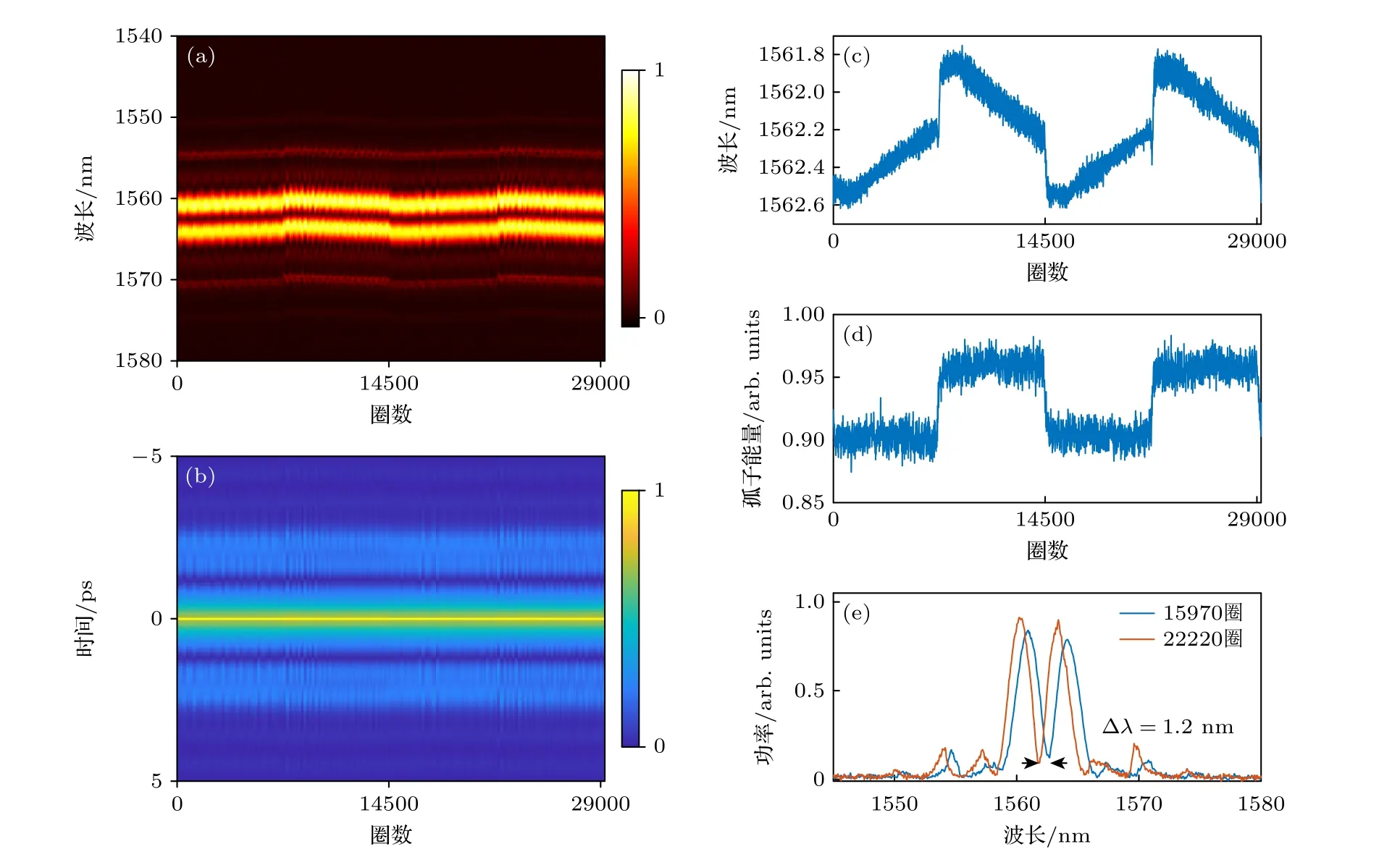
图3 当泵浦调制频率为1 kHz 时,孤子分子演化实验结果 (a) DFT 光谱随运行圈数的演化;(b) 对应的一阶自相关演化;(c) 脉冲能量演化;(d) 光谱中心波长的脉动演化;(e) 第15970 圈的DFT 光谱和第22220 圈的单次DFT 光谱Fig.3.Output characteristics of bound solitons at 1 kHz pump modulation frequency: (a) Evolution of DFT spectra with the number of cycles in operation;(b) corresponding first-order autocorrelation evolution;(c) pulse energy evolution;(d) pulsation evolution of spectral center wavelength;(e) DFT spectrum of lap 15970 and the single DFT spectrum of lap 22220.

图4 给出了调制频率为5 kHz 条件下孤子分子光谱演化实验结果,也观察到了光谱周期性蓝移/红移的脉动演化.不同的是,在周期性泵浦功率变化引发的光谱跳变同时,激发了周期性的光谱调制条纹,这说明形成了三孤子分子.调制频率的增加可以理解为对腔内增加了微扰产生频率[19],提高了腔内能量变化速率,使脉冲状态发生了改变.图4(a)表明光谱脉动的幅度为0.802 nm,脉动周期为200 μs,与调制信号周期一致(200 μs).图4(b)的自相关轨迹中周期性地出现5 个自相关旁瓣峰值,表明出现了第三个孤子的产生和湮灭[20].这种脉冲振荡几乎会持续半个周期,孤子间距在57—62 ps 内变化(图4(f)),且只在泵浦功率处于低功率时产生,处于高功率时湮灭.对比图4(c),(d),不难看出孤子分子的能量和光谱变化的特点和趋势与之前相同.图4(e)中给出了孤子相对相位随圈数的变化,需要说明的是,该相对相位是第一个孤子和第三个孤子间的相对相位,即调制条纹的相位变化,而不是第一个孤子和第二个孤子的相对相位(即孤子分子的光谱包络变化),下同.可以看到静止相位和负相位交替转变,相对相位演化图呈阶梯式.信号发生器控制的增益能量对孤子间的相对相位演变产生影响,由于负相位孤子分子能量阈值低于静止相位孤子分子,导致其在静止孤子分子和负相孤子分子之间切换,并且提高泵浦功率会破坏这种负相孤子分子的滑动相位[21].文献[21]也说明负相位孤子分子更容易在低功率产生,而正相位孤子分子更容易在高功率产生.一旦泵浦功率发生改变,由于弛豫效应,脉冲能量会缓慢地损失和增长,使得这种相位变化与泵浦变化并非严格同步.图4(g)是两种典型情况下DFT 光谱的对比.与1 kHz 相比,5 kHz 的腔内能量波动更加频繁,使得由增益诱导的孤子分子光谱脉冲出现了三孤子分子,而这种变化原因在于调制频率的上升导致腔内增益流更不稳定,这对Er3+集居反转数的变化引起的增益谱重塑过程更加复杂.

图4 5 kHz 泵浦调制频率时孤子分子输出特性 (a) DFT 光谱随运行圈数的演化;(b) 对应的一阶自相关演化;(c) 脉冲能量演化;(d) 光谱中心波长的脉动演化;(e) 相对相位演化图;(f) 脉冲间距;(g) 10290 圈单次光谱和10910 圈单次光谱Fig.4.Output characteristics of bound solitons at 5 kHz pump modulation frequency: (a) Evolution of DFT spectra with the number of cycles in operation;(b) corresponding first-order autocorrelation evolution;(c) pulse energy evolution;(d) pulsation evolution of spectral center wavelength;(e) relative phase evolution diagram;(f) pulse spacing;(g) 10290 cycles and 10910 cycles of single spectrum.

图5 为调制频率为20 kHz 下双稳态孤子分子锁模实验结果.图5(a)为DFT 实时光谱的演化,揭示了光谱脉冲由此前的周期性阶梯似的蓝移/红移转变为连续周期性的蓝移/红移,且脉动频率与调制频率相同.光谱脉动幅度为0.789 nm (图5(d)).尽管光谱中心波长脉动(图5(d))以及孤子间相对间距(图5(f))的演化依然呈现出周期性振荡,但相对变化幅度减小.图5(g)给出了两种典型情况下的光谱,证明了孤子分子光谱脉动.值得注意的是,在20 kHz 调制频率下,腔内孤子总能量随时间的演化虽呈现出周期性,但也表现出了一定的不稳定性,如图5(c)所示.此外,孤子分子内部孤子间相对相位的演化也失去了周期性而呈现出负相位发散态[14].这些现象可能是由于高调制频率情况下,泵浦激光器功率输出的不稳定性以及腔内非线性动力学瞬态变化所引起的.

图5 20 kHz 泵浦调制频率时孤子分子输出特性 (a) DFT 光谱随运行圈数的演化;(b) 对应的一阶自相关演化;(c) 脉冲能量演化;(d) 光谱中心波长的脉动演化;(e) 相对相位演化;(f) 脉冲间距;(g) 2850 圈单次光谱和3076 圈单次光谱Fig.5.Output characteristics of bound solitons at 20 kHz pump modulation frequency: (a) Evolution of DFT spectra with the number of running cycles;(b) corresponding first-order autocorrelation evolution;(c) pulse energy evolution;(d) pulsation evolution of spectral center wavelength;(e) relative phase evolution diagram;(f) pulse spacing;(g) 2850 cycles and 3076 cycles of single spectrum.

综上,在较低的调制频率下,由于腔内能量积累和泵浦功率的稳态处于主导地位,由电平切换带来的微扰对孤子分子的双稳态更加明显,因此波长变化较大,最大波长漂移为1.20 nm.而较高频率使EDF 的集居数反转加快,由EDF 的瞬态增益使得泵浦功率的瞬态变换逐渐处于主导地位,孤子能量和腔内能量积累减弱,弛豫效应影响增强,所以波长变化较小,波长漂移在0.7—0.9 nm 之间.虽然此时脉动光谱中心波长和孤子间距演化与泵浦功率、调制信号同步,但孤子间相对相位的演化失去了周期性,与调制信号不同步.孤子分子内脉冲间的相对相位演化逐渐趋于混乱,这表明脉动孤子分子可能存在固有的共振频率,与孤子分子的稳定性有关.

4 结论

本文利用DFT 技术,研究了一种基于泵浦强度调制的超快掺铒光纤锁模激光器中孤子分子光谱脉动动力学.通过对泵浦源驱动电压进行调控,探讨了外部调制信号对孤子分子光谱脉动的幅度与周期、脉动频率以及脉动孤子分子内部孤子间相对相位演化的影响,揭示了周期性光谱脉动的孤子分子以及不同相位演化的光谱脉动孤子分子态之间的切换.研究结果对深入理解孤子间相互作用以及超快激光器内在的物理机制,实现全光操控等具有重要意义,对孤子分子在编码和可调谐激光器等应用方向具有指导作用.