基于改进鲸鱼算法的多无人机协同欺骗干扰技术*
2024-01-24丁宸聪叶紫晴
丁宸聪,叶紫晴
(中国人民解放军92728部队,上海 200442)
0 引 言
在现代电磁频谱作战环境中,利用多架无人机协同干扰的方式对组网雷达进行航迹欺骗已成为近年来新的作战趋势,相较于单架无人机而言,多机协同能使得欺骗干扰效果更加显著[1-2]。多无人机协同欺骗干扰需要对研究问题进行数学建模并对目标函数进行合理优化,而多无人机协同干扰组网雷达问题多为非连续、多参数以及多约束问题,故在优化时往往需要利用群体智能算法进行求解。为了有效地对组网雷达实施干扰,文献[3]根据航迹欺骗干扰原理和无人机任务特点,对无人机实施航迹欺骗干扰模型进行了简化,并给出了模型求解流程。文献[4]针对多无人机协同干扰组网雷达问题对无人机协同飞行进行了建模,并利用遗传算法对目标函数进行了最优化求解。文献[5]根据预设虚假航迹,分析了多无人机运动约束,对多无人机协同航迹欺骗问题进行了建模,同时给出了无人机航迹欺骗干扰策略和运动方式的编码描述方法,最后采用改进差分进化算法对无人机协同航迹欺骗策略进行了优化求解。
群体智能算法是依据自然界某些生物种群的特殊群体行为而人为抽象出来的算法,广泛地运用于多个领域[6]。然而传统的群体智能算法如粒子群(Particle Swarm Optimization,PSO) 算法、蚁群算法(Ant Colony Algorithm,ACA)等在求解大规模优化问题时往往存在算法效率低、求解精度差以及容易陷入局部最优等问题,因此近年来大量新型群体智能算法先后被有关学者提出。标准鲸鱼优化算法(Whale Optimization Algorithm,WOA)作为新型群体智能算法的典型代表,其性能要优于传统群体智能算法,目前已被运用到图像分割、盲源分离等领域并取得了显著效果[7-8]。但由于算法本身也存在收敛速度慢、求解结果精度低等缺点[9],为了得到更好的优化结果,本文对标准鲸鱼优化算法进行了改进。利用改进鲸鱼优化算法(Improved Whale Optimization Algorithm,IWOA)、标准鲸鱼算法、粒子群算法以及蚁群算法分别对多机协同欺骗干扰模型进行优化,通过仿真实验对比和分析了4种算法寻优性能的差异性。
1 多机协同航迹欺骗干扰原理
多无人机协同航迹欺骗干扰主要利用多架无人机通过协同作战的方式对组网雷达系统进行欺骗干扰,无人机携带的干扰载荷可采用数字射频存储技术(Digital Radio Frequency Memory,DRFM)将接收到的雷达信号进行存储和延迟转发,使得雷达能够接收到一个或多个位于雷达与无人机连线上的回波信号[10-11]。在组网雷达系统中,真实目标与有源假目标在空间状态上存在显著差异,利用组网雷达真假目标空间状态差异来识别虚假目标的方法被称为“同源检验”,它是组网雷达系统识别真假目标的理论基础[12-13]。组网雷达系统信息融合中心基于一定的“同源检验”融合规则,对接收到的多部雷达在统一坐标系下的同一空间位置上检测到的目标信号,判断其是否为一个合理的目标航迹点,多个连续的合理目标航迹点就形成了目标航迹。图1为多架无人机对组网雷达系统进行协同欺骗干扰的示意图。
2 无人机航迹动力学优化问题
本文假设组网雷达系统共有5部雷达,每部雷达的数据更新率为10 s,规定只要有3部或3部以上雷达检测到的航迹点状态信息在统一的空间坐标系中一致,则融合中心便认为该航迹点合理,并假设20个连续的航迹点便能在融合中心建成一条航迹。因此本文将多机协同航迹欺骗干扰抽象为无人机航迹动力学优化问题,并建立了无人机航迹优化数学模型、约束条件以及对应的目标优化函数。
2.1 模型假设
假设1:无人机的雷达散射截面积较小且具有较强隐身能力,被组网雷达系统检测到的概率可以忽略,并且同一时刻一架无人机只能干扰一部雷达。
假设2:无人机的飞行速度、飞行高度、最大加速度、转弯半径以及无人机间距均控制在合理的范围内。
假设3:组网雷达系统中各部雷达的最大作用距离均为150 km,无人机进行航迹欺骗时需产生一条预先设定好的假目标航迹,并且干扰总时长假定为200 s。
2.2 数学模型
图2为无人机产生欺骗干扰航迹的数学模型示意图,根据“同源检验”规则要求,假目标航迹上的每个点处均有至少3条雷达与无人机延长线相交。当被欺骗的3部雷达与其对应的虚假航迹点确定时,则可根据无人机的飞行高度计算得出无人机在统一空间坐标系中的具体位置。

图2 无人机产生欺骗干扰航迹数学模型示意图Fig.2 Mathematical model of the deception jamming track generated by UAVs
为了利用无人机尽可能多地产生假目标航迹,需要对无人机的飞行策略进行优化。本文对无人机的协同策略作出如下假定:
1)无人机在某时刻对某部雷达进行欺骗干扰时,可根据需要对雷达回波信号进行多次延迟转发,使得该部雷达在该时刻能够接收到一个或多个位于雷达与无人机连线上的回波信号,其他无人机可利用该时刻多余的回波信号寻找生成新假目标点的机会;
2)记在某时刻无人机需要位于某个空间位置对雷达进行欺骗干扰为一次飞行任务,若在两个时刻间飞行任务符合无人机本身的动力学约束,则无人机继续执行任务;反之,该无人机则放弃执行该任务,此时调动其他空闲无人机执行原任务。
2.3 约束条件及目标优化函数

1)无人机编队数量固定,无人机飞行速度v、高度h以及无人机的转弯半径Ra均设置为合理范围;

3)根据组网雷达系统“同源检验”规则,同一时刻至少有3架无人机对组网雷达进行干扰。
综上所述,本文建立的无人机航迹动力学目标优化函数如下:
(1)
3 改进鲸鱼优化算法及模型求解
3.1 标准鲸鱼算法
鲸鱼优化算法分为3个阶段。第一阶段为座头鲸识别并包围猎物,该行为由以下规则建模:
x1(t+1)=x*(t)-a·d
(2)
d=|c·x*(t)-x(t)|
(3)
a=2ρ·r-ρ
(4)
c=2·r
(5)
(6)
式(2)~(6)中:d表示鲸鱼个体与猎物之间的距离向量;t表示当前迭代次数;a和c为系数向量,控制鲸鱼的游走方式;ρ为控制参数,在迭代过程中从2线性减少到0;N为最大迭代次数;r为[0,1]上的随机向量;x*为最佳解的位置向量,x为当前位置向量。
第二阶段为局部搜索阶段,座头鲸进行气泡网攻击,具有“收缩包围”和“螺旋更新位置”两种机制,其中“螺旋更新位置”机制迭代规则如下:
x2(t+1)=dT·ebl·cos(2πl)+x*(t)
(7)
dT=|x*(t)-x(t)|
(8)
式中:dT表示表示鲸鱼个体与猎物之间的距离向量;随机数l∈[-1,1];常数b反映对数螺线形状。
座头鲸接近猎物时,其收缩包围和螺旋更新位置行为是同时进行的,本文假定座头鲸各有50%的概率进行收缩包围和螺旋更新位置,其数学模型描述如下:
(9)
式中:p为[0,1]上的随机数。
第三阶段为全局搜索阶段,座头鲸根据同类位置进行随机搜索,规则如下:
x(t+1)=xrand-a·drand
(10)
drand=|c·xrand-x(t)|
(11)
式中:drand表示随机选取的鲸鱼个体到猎物的距离向量;xrand表示随机选择的鲸鱼个体位置向量。
3.2 改进鲸鱼优化算法
为了提高鲸鱼优化算法的全局搜索能力,提升算法的寻优速度,本文考虑引入合适的惯性权值。由于标准鲸鱼优化算法的权重值始终为1,导致其只在最优解附近寻优,无法满足算法运行的实际情况。根据较大权值全局寻优能力强、较小权值局部寻优能力差的特点,本文引入了一种基于指数函数的自适应的动态惯性权重因子ε,公式如下:
(12)
式中:ε为自适应惯性权重因子;t为当前迭代次数;N为最大迭代次数。
由式(12)可知,自适应权重ε会随迭代次数t的增加而增大。权重因子在迭代前期较小,对鲸鱼个体位置更新影响较小,但在寻优后期,较大的权重因子会加快鲸鱼位置的移动速度,从而使得算法的寻优能力增加。改进后的鲸鱼优化算法位置更新公式如下:
x(t+1)=εx*(t)-a·d
(13)
x(t+1)=εdT·ebl·cos(2πl)+(1-ε)x*(t)
(14)
x(t+1)=εxrand-a·drand
(15)
3.3 基于改进鲸鱼优化算法的求解步骤
假设无人机编队U={U1,U2,…,US}由S架无人机组成,预设假目标航迹L1={P11,P12,…,P1m}由m个假目标航迹点组成,无人机协同欺骗产生的新航迹初始设置为L2={P21,P22,…,P2m},……,Ln={Pn1,Pn2,…,Pnm}共n-1条。首先利用无人机产生航迹L1,根据“同源检测”规则可知,至少需要3架无人机才能完成该任务。随后利用剩余的无人机在满足自身飞行约束条件的前提下产生新的假目标航迹,最后统计总共产生的航迹条数。定义Fij为无人机从i时刻的空间位置飞行至j时刻的空间位置,若两者为可行线,则Fij+1,记录该条飞行线路;否则剔除,保持Fij不变,判断下一个目标点。利用改进鲸鱼优化算法对多机协同欺骗干扰模型进行求解的具体步骤如下:
步骤1 输入5部组网雷达坐标、航迹点数m、航迹条数n、无人机的数量S以及预设假目标航迹参数。初始化无人机飞行高度为2 km,设置无人机起始坐标,同时初始化鲸鱼群体数量以及最大迭代次数。
步骤2 利用3架无人机{U1,U2,U3}对组网雷达进行欺骗干扰,产生航迹L1。记航迹L1上Pi点对应i时刻无人机的空间位置,Pj点对应j时刻无人机的空间位置。利用Fij记录m个时刻内所有可行线,将无人机所有飞行任务所对应的空间位置按照时刻的先后顺序表示为求解空间T。
步骤3 根据式(1)中无人机的飞行动力约束条件利用改进鲸鱼算法对步骤2中的求解空间T中的无人机飞行空间位置进行优化,确定无人机的最优飞行轨迹,并且记录3架无人机在0~m时刻的飞行坐标。
步骤4 利用剩余的无人机{U4,U5,…,US}产生新假目标航迹。利用航迹L1上m个时刻对应的3架无人机能生成更多假目标点的特点确定剩余无人机飞行任务所对应的飞行空间位置,并且利用Fij记录m个时刻内所有可行线,将剩余无人机所有飞行任务所对应的空间位置按照时刻的先后顺序表示为求解空间Q。
步骤5 根据式(1)中航迹条数作为优化模型的适应度函数,式(1)中的约束条件为前提,对求解空间Q内的航迹进行优化,并计算每个鲸鱼个体的适应度值。
步骤6 更新鲸鱼群体中所有鲸鱼个体的位置。当p<0.5且|a|<1时,按照式(13)更新个体位置;当p≥0.5时,按照式(14)更新个体位置;当p<0.5且|a|≥1时,按照式(15)更新个体位置。
步骤7 记录更新后最优适应度值和对应航迹向量,同时更新参数ρ,a,c,l,p,ε。
步骤8 每更新一条完整的假目标航迹,n的值不变;反之,n的值减1。
步骤9 若L2~Ln每条假目标航迹更新完毕,则求解过程结束,输出最终n的值,L2~Ln的航迹点坐标以及无人机{U4,U5,…,US}的飞行坐标;若不满足,则跳回步骤6,直到满足迭代次数为止。
4 优化算法仿真及其效率评价
4.1 仿真实验参数设置
本文所有的仿真实验均在相同的测试平台上运行,硬件测试环境为Intel(R) Core(TM) i5-10400F CPU @ 2.9 GHz,软件编程环境为Matlab R2018b。假设某组网雷达系统5部雷达的空间位置坐标(单位:km)分别为R1(80,0,0),R2(30,60,0),R3(55,110,0),R4(105,110,0),R5(130,60,0)。利用首点迭代法[14]产生如图3所示的一条预设假目标欺骗航迹,其中虚假航迹点初始位置坐标为(60 600 m,69 982 m,7 995 m)。假设该点与5部雷达的连线分别与h=2 km的平面交于5点,则无人机的初始位置设定位于该5点构成的几何图形的中心处。并且假定无人机编队数量为9架,取Δt=10 s,T=200 s,即组网雷达探测时间间隔为10 s,无人机飞行时间为200 s。利用4种群体智能算法求解多机协同欺骗干扰模型的初始参数设置如下:
粒子群算法初始参数设置为,迭代次数N=100,种群数量M=50,欺骗航迹条数初设为L=20,惯性权重ω=1.2,学习因子c1=c2=2。
蚁群算法初始参数设置为,迭代次数N=100,蚁群数量M=100,欺骗航迹条数初设为L=20,信息启发因子α=2,期望启发因子β=3,信息素挥发系数ρ=0.5。
鲸鱼算法以及改进鲸鱼算法的初始参数均设置为,迭代次数N=100,种群数量M=100,欺骗航迹条数初设为L=20。

图3 预设假目标欺骗轨迹示意图Fig.3 Preset false target deception track diagram
4.2 仿真实验结果
利用蚁群算法[15]、粒子群算法[16]、标准鲸鱼算法[17]以及本文提出的改进鲸鱼算法分别对多机协同欺骗干扰模型进行优化求解,仿真结果表明,在初始设定欺骗航迹条数L=20的条件下,利用9架无人机组成的编队对组网雷达进行航迹欺骗干扰,4种算法优化求解结果均为最多产生4条虚假航迹。4种算法的适应度值收敛曲线如图4所示,利用标准鲸鱼算法与改进鲸鱼算法优化产生的假目标航迹如图5和图6所示。
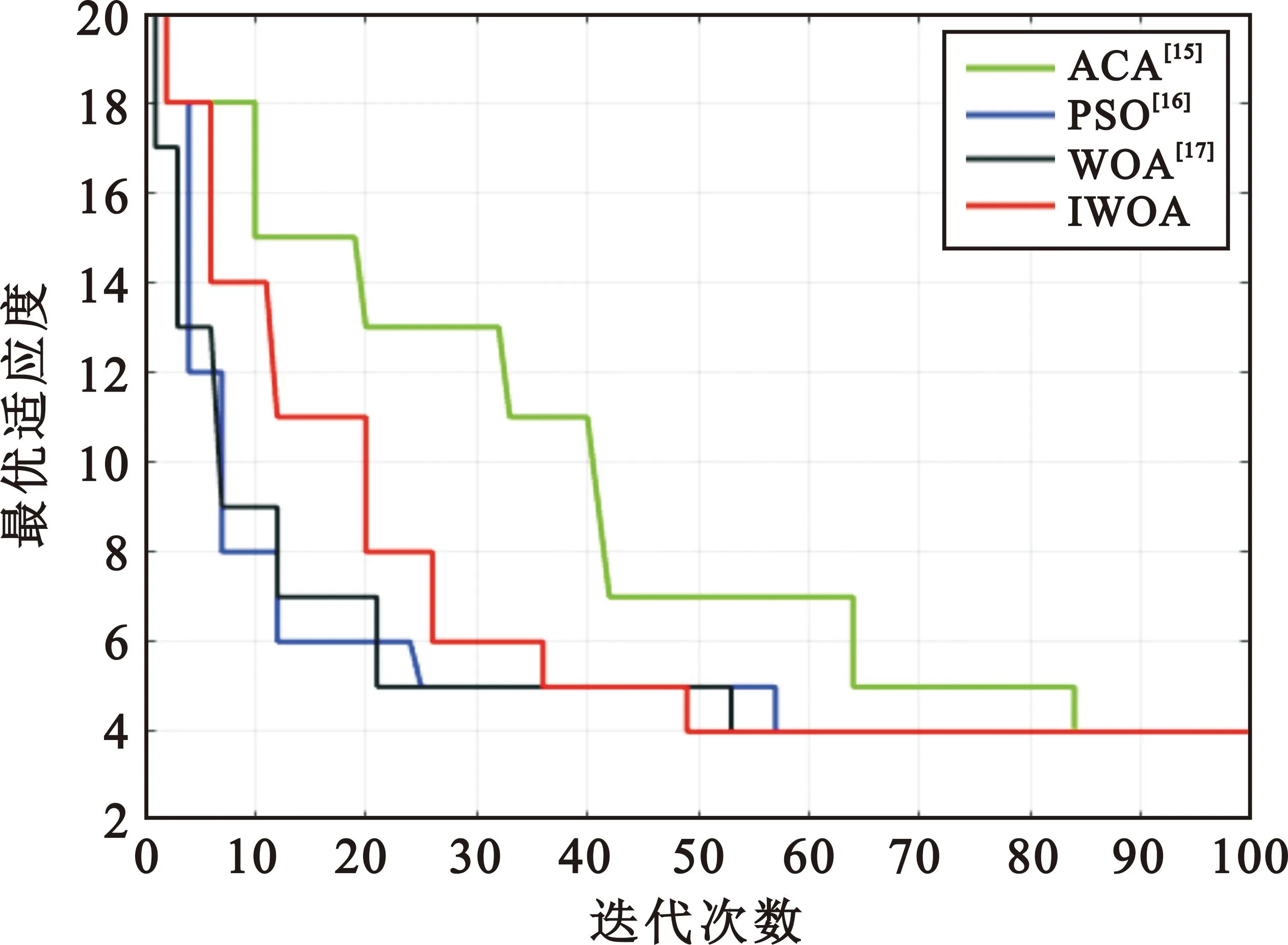
图4 4种优化算法适应度值收敛曲线Fig.4 Fitness value convergence curves of four optimization algorithms
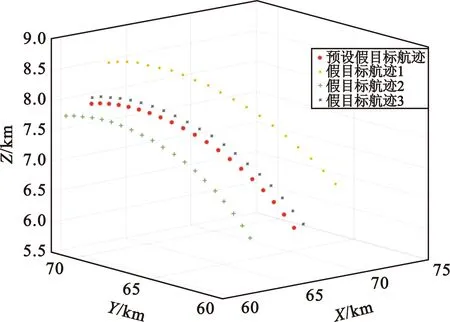
图5 鲸鱼算法产生假目标航迹图Fig.5 False target tracks generated by WOA

图6 改进鲸鱼算法产生假目标航迹图Fig.6 False target tracks generated by IWOA
4.3 算法分析与评价
4.3.1 算法效率
采用4种算法对多机协同欺骗干扰模型进行优化求解的平均执行时间以及最大迭代次数如表1所示。分析表中数据可以得出,改进鲸鱼优化算法相较于粒子群算法、蚁群算法以及标准鲸鱼算法平均执行时间短,收敛到最小值时的迭代次数少,进而得出4种算法的求解效率为IWOA>WOA>PSO>ACA。

表1 4种算法运行效率对比Tab.1 Operating efficiency comparison among four algorithms
4.3.2 算法求解精度
为了比较4种算法在优化多机协同欺骗干扰模型时的求解精度,本文通过预设航迹点的理论值与算法实际产生的航迹点的误差值的大小来反映4种算法性能的差异,并定义了式(16)来具体表征算法产生的实际航迹与理论值的误差大小。
(16)
式中:(xi0,yi0,zi0)与(xi,yi,zi)分别表示i时刻理论航迹点与实际产生航迹点的坐标值。本文对4种优化算法产生的航迹与理论预设的航迹进行了误差对比,结果见表2。分析表中数据可以得出,改进鲸鱼优化算法相较于其他3种算法产生的航迹与理论航迹的误差值最小,算法的求解精度最高。

表2 4种算法性能对比Tab.2 Performance comparison among four algorithms
4.3.3 算法全局寻优能力
改变无人机编队的数量,利用4种算法求解在不同无人机架数的条件下各自算法的最优适应度值,结果如图7所示。由图可知,利用群体智能算法求解多机协同欺骗干扰模型时,随着无人机编队数量的增加,粒子群算法和蚁群算法的全局搜索能力开始变弱,即算法的全局寻优能力会随无人机编队数量的增加而降低;相反,标准鲸鱼算法和改进鲸鱼优化算法在同等条件下处理较大规模优化问题时,能表现出较好的全局搜索能力,并且改进鲸鱼优化算法相较于标准鲸鱼算法具有更高的求解精度,算法的寻优性能更强。
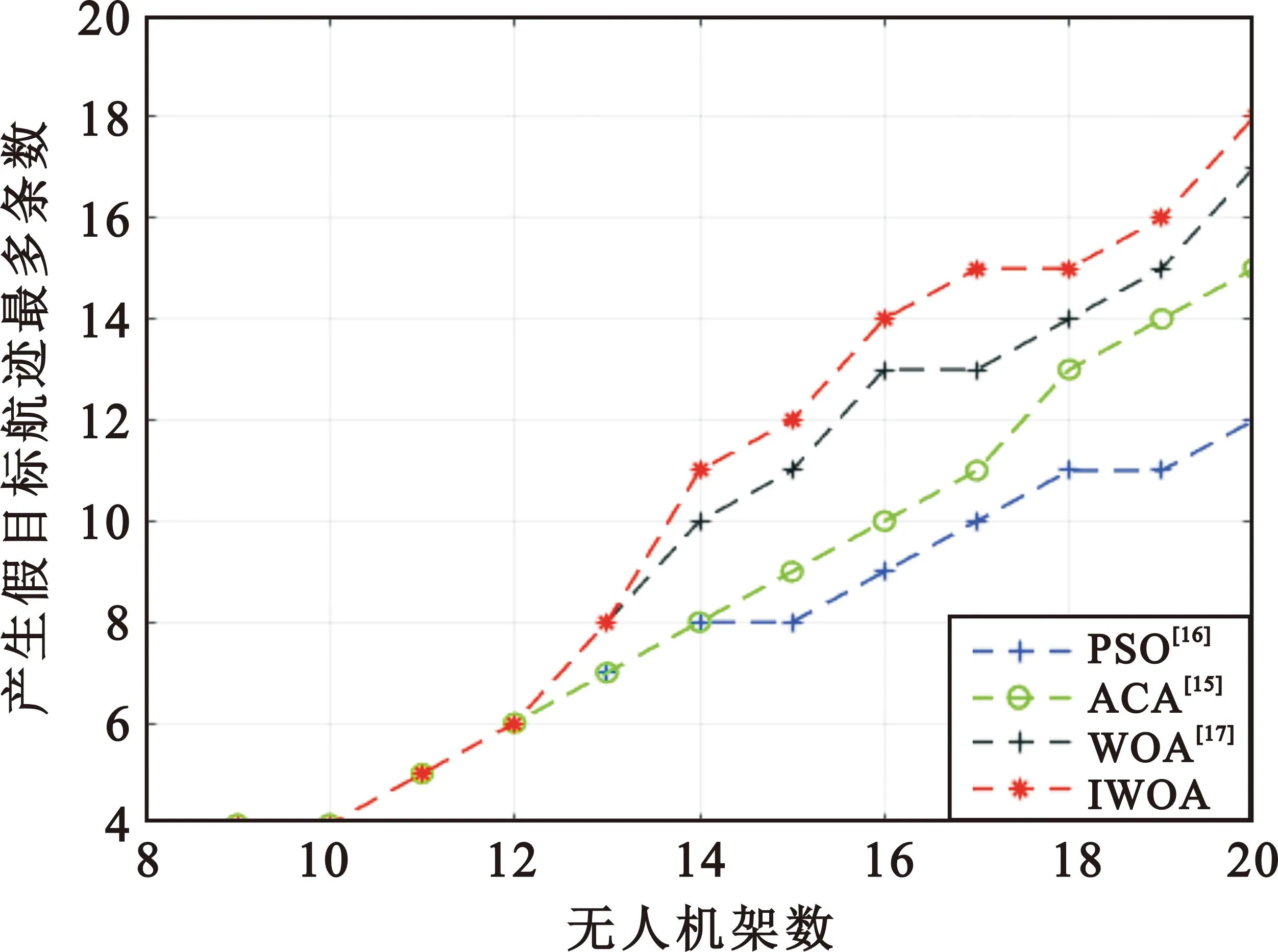
图7 4种算法在不同无人机数量下的最优适应度值Fig.7 The optimal fitness values of the four algorithms under different number of UAVs
5 结束语
多机协同对组网雷达的航迹欺骗干扰需要考虑组网雷达系统的“同源检测”规则,属于大规模无人机航迹动力学优化问题。为了得到更好的优化结果,本文提出了一种基于改进鲸鱼优化算法的多无人机协同干扰技术,并且通过仿真实验验证了改进鲸鱼优化算法在求解多无人机航迹动力学优化模型时算法效率、算法精度以及算法的全局寻优能力均优于本文中的3种对比算法,对于利用无人机对组网雷达系统进行协同欺骗干扰具有一定的参考价值。
为了进一步获得理想的求解效果,后续工作可以考虑设计更加高效的算法,以达到快速收敛的同时避免陷入局部最优解。
