地质突变条件下基于组合模型的围岩等级和TBM掘进参数预测

满 轲,曹子祥,刘晓丽,宋志飞,柳宗旭,刘汭琳,武立文

(1.北方工业大学土木工程学院,北京 100144; 2.清华大学水沙科学与水利水电工程国家重点试验室,北京 100084)

硬岩隧道掘进机(TBM)施工具有可连续操作、机械化程度高、开挖速度快、工程质量高等优点,已被广泛应用于深埋隧道的施工中[1-2]。TBM多应用于城市地铁、穿山隧道和深地实验室等工程,这些工程所处的地质环境均较复杂。当TBM施工遇到地质突变时,仅依靠主司机的施工经验进行掘进参数调整会大幅降低工程的掘进效率和安全性[3-4]。TBM开挖深埋隧道时,围岩等级的变化会产生一系列的深部岩石力学问题,如果处理不当会出现坍塌、卡机、埋机等事故[5-6]。因此,有必要对地质突变条件下,掌子面前方的围岩等级和TBM掘进参数进行预测,以指导主司机科学地调整掘进参数,并辅助施工人员采取较安全的围岩支护方式。

近年来,众多学者采用机器学习算法分析TBM掘进参数与围岩地质情况的相关性来预测TBM掘进参数和围岩等级[7-10]。围岩等级预测方面:张海龙等[11]基于TBM掘进参数(推力、扭矩、贯入度),构建了围岩强度快速估算的新方法;卢瑾等[12]通过3DEC建立了TBM滚刀破岩三维仿真模型,分析了不同地质条件对TBM掘进速率的影响;Liu等[13]通过构建SA-BPNN模型,对单轴抗压强度、脆性指数、薄弱面之间的距离、不连续面的方向4个岩体参数进行了预测分析;李宏波[14]以推力切深指数(FPI)和刀盘扭矩旋转切深指数(TPI)为输入参数,通过自组织神经网络聚类和最小二乘支持向量机的组合模型(SOM-SVM)改进围岩等级识别预测,对Ⅱ、Ⅲ、Ⅳ级围岩识别的平均准确率为83.67%;张娜等[15]以花岗岩和石灰岩地层为例,分别采用分步回归法和聚类分析法对岩石单轴抗压强度、岩体体积节理数和围岩等级进行预测,岩石单轴抗压强度和岩体体积节理数的预测结果误差均小于18%,围岩等级预测值与实际值基本相符;奚明华[16]通过对不同围岩条件下TBM掘进参数和掘进载荷分布规律的分析,利用随机森林算法以刀盘转速、刀盘扭矩、推进速度、总推进力为输入,围岩等级为输出,建立了围岩等级识别模型,识别准确率高达98.8%。掘进参数预测方面:闫长斌等[17]基于岩体指标和TBM掘进参数构建了多元非线性回归TBM净掘进速率预测模型,总体预测误差未超过10%;Mahdevari等[18]基于岩体特性和TBM掘进参数运用SVR模型预测了掘进速度,预测结果的均方误差为0.0013、拟合优度R2为0.9903;Zhu等[19]利用人工神经网络模型将刀盘扭矩、刀盘转速、总推力和推进速度作为输入变量,对净掘进速度进行预测分析,最终验证了通过历史数据预测TBM掘进性能的可能性;罗华等[20]建立了以岩石饱和单轴抗压强度和完整性系数为变量的TBM掘进速率经验模型,并对吉林引松供水隧道工程的掘进参数贯入度、推力、扭矩进行了预测,预测结果的平均相对误差均小于15.5%;张哲铭等[21]基于最小二乘支持向量机(LS-SVM)算法构建了TBM掘进参数(推进速度、刀盘转速、总推力、刀盘扭矩)的预测模型,其中刀盘转速和总推力预测结果的R2均大于0.8;Ma等[22]基于秦岭隧道南段施工数据,采用随机森林算法选取了影响TBM掘进速度的主要特征因素:推力、转速、单轴抗压强度、体积节理数,利用BPNN模型和SVR模型对推进速度进行预测分析;Gao等[23]采用RNN模型、LSTM模型、GRU模型实现了扭矩、速度、推力、腔室压力的实时预测,预测精度高于多元回归模型,并且可以对TBM掘进时采集的时间连续原位数据进行分析和预测;Zhang等[24-25]分别提出了BiGRU-ATT模型和PSO-BiLSTM模型,可对刀盘扭矩、推进速度、总推力、刀盘功率进行准确预测。

现有对围岩等级和TBM掘进参数的预测多数是采用传统机器学习算法,这些算法并没有充分利用TBM掘进参数数据集的历史信息,预测准确度偏低。利用优化算法与深度学习算法结合的TBM掘进参数预测模型的输入参数较多,模型复杂,导致模型在其他工程中应用的难度较大。由于实际工程中的岩体参数是通过实验室测得的,与岩体真实值存在一定误差,所以将岩体参数作为预测模型输入会进一步增大预测误差,预测结果对实际工程的指导意义较小。并且现在地质突变条件对围岩等级和TBM掘进参数预测的影响(有利或无利)研究较少。

为了充分利用TBM掘进参数数据集的历史信息,充分发挥深度学习算法与传统机器学习算法各自的优势,本文构建了双向长短期记忆(bidirectional long short-term memory,BiLSTM)网络与支持向量机回归(support vector regression,SVR)算法相结合的BiLSTM-SVR模型,以期提高预测模型准确度和鲁棒性。目前,TBM隧道工程掘进参数预测研究最多的包括推力(F)、扭矩(T)、转速(N)、净掘进速度(νPR)和施工速度(νAR)[24,26-29],又由于掘进参数开挖比能(ESE)对工程中围岩支护和成本控制具有重要影响,故选择掘进参数F、T、νPR、νAR、N、ESE进行研究,将其作为BiLSTM-SVR模型的输入变量,实现对围岩等级和各个掘进参数的预测。

1 BiLSTM-SVR模型

TBM掘进过程中,掘进参数数据集具有明显的时序性。由于TBM掘进参数是围岩和TBM之间相互作用的结果[30-31],因此掘进参数可以反映围岩地质信息。BiLSTM网络和SVR算法都已在掘进参数的时间序列样本预测上取得了较好成果[32-34]。

1.1 BiLSTM网络

循环神经网络(recurrent neural networks,RNN)可以对具有时间序列的样本进行预测,但当处理较长序列样本时,RNN训练时往往会出现样本信息梯度消失或梯度爆炸现象,严重影响训练效果[35]。因此,在RNN的隐藏层节点上引入“门”控操作,产生了一种长短期记忆(long short-term memory,LSTM)网络[36],引入的“门”控操作较大地提高了神经网络的性能。

双向循环神经网络((bidirectional recurrent neural networks,BRNN)是在RNN结构基础上加了一个反向循环传播层,双向传播网络结构可以同时利用前向传播和反向传播的信息。基于BRNN结构,将LSTM单元代替RNN单元,从而形成了BiLSTM网络。BiLSTM网络可以弥补LSTM不能进行反向传播信息的缺点[37]。BiLSTM网络隐藏层输出值的具体计算方法见文献[25,32,38]。

1.2 SVR算法

SVR算法在没有增加计算复杂度的同时通过非线性映射方法将训练样本映射到高维空间,在高维空间实现样本的线性或非线性回归。SVR算法对中、小规模数据样本集的学习效果较好,可以有效解决神经网络算法中经常出现的局部极值问题,引入的核函数有效避免了维度灾难问题[39]。SVR算法详细推导过程见文献[35]。

1.3 BiLSTM-SVR模型构建

用于围岩等级预测和TBM掘进参数预测的BiLSTM-SVR模型预测流程如图1所示。

图1 BiLSTM-SVR模型预测流程Fig.1 Prediction process of BiLSTM-SVR model

各数据集在进行BiLSTM-SVR模型的训练之前先进行归一化处理[38],达到消除数据间量纲差异的目的。归一化处理之后的训练集数据通过BiLSTM模型和SVR模型的训练分别得到各自模型的输出值,以BiLSTM模型和SVR模型预测结果的误差绝对值最小为损失函数,通过该损失函数确定各单一模型的最优权重(式(1)),最后BiLSTM-SVR模型利用训练集计算出的最优权重进行测试集数据预测,得到围岩等级预测值和TBM掘进参数预测值。

(1)

2 BiLSTM-SVR模型验证

2.1 工程概况及数据集建立

本文的工程背景为新疆某引水隧洞工程,隧洞埋深为200～700m,标段全长为34.751km,开挖断面直径为7.8m;TBM型号为QJYC078。本标段利用BQ法进行隧道围岩稳定性评价,主要分为Ⅱ级、Ⅲ级和Ⅳ级,再进一步将Ⅲ级围岩细分为Ⅲ-a级围岩与Ⅲ-b级围岩。TBM主要技术参数及掘进数据集参见文献[40],其中Ⅱ级围岩掘进数据共67组、Ⅲ-a级围岩掘进数据共75组、Ⅲ-b级围岩掘进数据共61组、Ⅳ级围岩掘进数据共53组。

为了使现有的各单一围岩等级达到地质突变条件,将各围岩等级(Ⅱ级、Ⅲ-a级、Ⅲ-b级和Ⅳ级)进行排列组合,共形成了24种组合类型,见表1。各地质突变类型的数据集由各单一围岩等级数据集的前50组数据构成,共200组数据,其中训练集180组数据,测试集20组数据。将Ⅱ级、Ⅲ-a级、Ⅲ-b级、Ⅳ级围岩等级用数值1、2、3、4替代,便于预测模型的预测值输出。

表1 围岩等级的组合类型Table 1 Combination form of surrounding rock grades

2.2 围岩等级预测

将F、T、νPR、νAR、N、ESE作为BiLSTM-SVR模型的输入变量,各围岩等级替代值作为BiLSTM-SVR模型的输出变量。

对训练集采用五折交叉验证法选取BiLSTM-SVR模型的参数值:BiLSTM模型设置3层隐藏层;最大迭代周期为800,学习率下降周期为500;初始学习率为0.005,学习率下降因子为0.2;模型采用Adam算法进行权重更新;模型的损失函数为均方误差。SVR模型的超参数C和γ采用网格搜索方法进行优化处理,其搜索范围为(2-10,210),搜索步距为20.5,RBF函数作为核函数。

选择均方根误差(RMSE)、平均绝对百分比误差(MAPE)和平均绝对误差(MAE)对预测围岩等级的准确度进行评价。RMSE、MAPE和MAE越小,均表明预测模型对测试样本的预测准确度越高。

由表2可知,BiLSTM-SVR模型对围岩等级的预测准确度较高,RMSE均小于0.0265、MAPE均小于0.95%:10、18、22、24组合的误差较大,MAPE均大于0.79%,即在地质突变条件下预测Ⅱ级围岩时准确度较低。Ⅲ-b级和Ⅳ级围岩预测时,各组合类型的误差均较小,MAPE基本小于0.4%,即在地质突变条件下预测Ⅲ-b级和Ⅳ级围岩时准确度较高。TBM开挖Ⅱ级和Ⅲ-a级围岩时,由于围岩稳定性高,掘进参数的波动范围较小,TBM在开挖Ⅲ-b级和Ⅳ级围岩时则相反。TBM掘进参数的波动范围越大、数据集越复杂,越有利于预测模型挖掘到岩机相互作用规律,但数据集信息过度复杂时会造成预测模型预测结果的过度拟合。当预测Ⅱ级和Ⅲ-a级围岩等级时,各种组合训练集的数据信息较复杂导致了BiLSTM-SVR模型的预测结果存在过拟合现象。

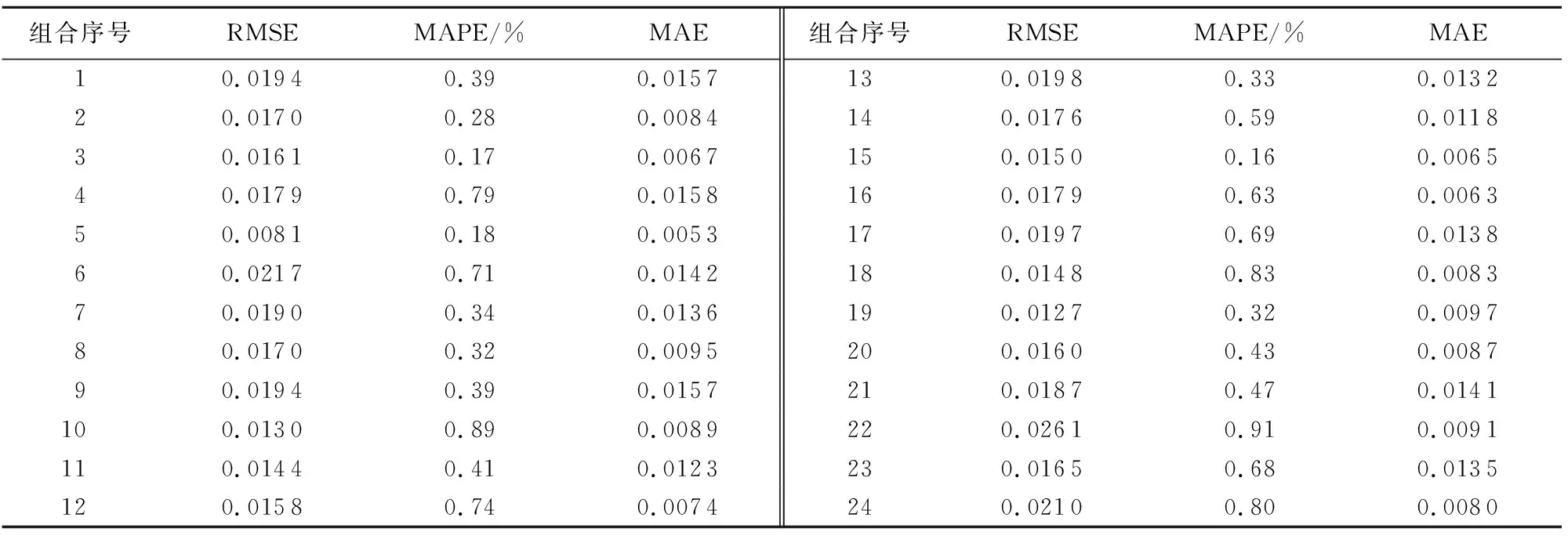
表2 BiLSTM-SVR模型预测围岩等级误差分析Table 2 Error analysis of predicting surrounding rock grades with BiLSTM-SVR model

BiLSTM-SVR模型预测围岩等级的结果看似过于理想(表2),主要原因包括该组合模型集成了BiLSTM模型和SVR模型各自的优势,模型的预测准确度和鲁棒性较高,对于挖掘复杂数据集输入特征与输出特征之间规律的能力更强;模型输入特征与输出特征之间的相关性较高(关联度均大于0.75),模型输入特征可以较准确地反映输出特征的变化趋势。但如果遇到更复杂的地质环境仍需对BiLSTM-SVR模型的预测效果做进一步的研究。

2.3 掘进参数预测

将掘进参数F、T、νPR、νAR、N、ESE作为BiLSTM-SVR模型的输入变量,依次取这6个参数之一作为BiLSTM-SVR模型的输出变量。

对训练集采用五折交叉验证法来选取BiLSTM-SVR模型的参数值:BiLSTM模型设置2层隐藏层;最大迭代周期为1000,学习率下降周期为700;初始学习率为0.005,学习率下降因子为0.2;模型采用Adam算法进行权重更新;模型的损失函数为均方误差。SVR模型的超参数C和γ采用网格搜索进行优化处理,其搜索范围为(2-10,210),搜索步距为20.1,Sigmoid函数作为核函数。

选择误差评价指标R2、RMSE、MAPE、MAE对BiLSTM-SVR模型预测各掘进参数的结果进行准确度评价。由图2可知,BiLSTM-SVR模型对F和T的预测准确度最高,对νPR和ESE的预测准确度最低。νAR的R2最大,RMSE、MAPE、MAE相对较小,即νAR的预测准确度相对较高。BiLSTM-SVR模型预测各掘进参数的R2平均值均大于0.8715、RMAE平均值均小于0.1722、MAPE平均值均小于0.5%、MAE平均值均小于0.1324。

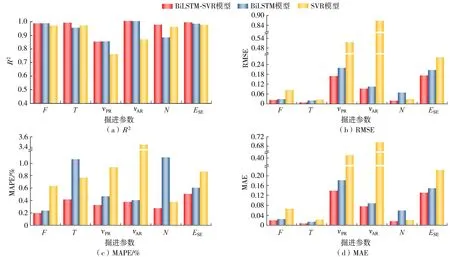
图2 各预测模型预测掘进参数误差平均值Fig.2 Average error of predicting tunnelling parameters for each prediction model

BiLSTM-SVR模型比单一BiLSTM模型和SVR模型的R2平均提高了6.53%,RMSE平均降低了41.96%,MAPE平均降低了40.60%,MAE平均降低了0.4101。BiLSTM-SVR模型的预测准确度高于单一的BiLSTM模型和SVR模型,即进行单一预测模型组合可以有效提高预测模型的预测准确度。TBM掘进参数数据集具有较强的时序性,因此可以充分利用BiLSTM网络具有记忆信息和拥有反向传播机制的优点;在现有数据集规模有限的情况下,也可以充分利用SVR算法适合中、小样本学习、强鲁棒性的优点。BiLSTM-SVR模型很好地整合了BiLSTM模型和SVR模型各自的优势,从而其预测准确度比单一预测模型高。BiLSTM模型的预测准确度高于SVR模型说明处理时序数据时预测模型具有记忆信息机制会提高模型的预测准确度。

定义最后2个围岩等级相邻时的组合形式为渐进突变,若不相邻则为间隔突变。由图2可知,渐进突变的组合形式相较于间隔突变的组合形式BiLSTM-SVR模型预测准确度更高。

围岩突变条件下围岩的稳定性较低,会加剧岩爆、突涌水、卡机等现象的出现,进而掘进参数的变化范围会加大。TBM掘进参数的波动范围越大、数据集越复杂,越有利于预测模型充分挖掘到岩机相互作用规律,但当数据集信息过度复杂时会造成预测模型过度拟合。当测试集的掘进参数数据来自Ⅱ级围岩和Ⅲ-a级围岩时,各种组合的训练集数据信息较复杂导致了BiLSTM-SVR模型的预测结果存在过拟合现象,预测准确度变低。同样当组合形式是间隔突变时,数据集信息较复杂使得BiLSTM-SVR模型的预测结果出现过拟合现象,导致预测准确度变低。

一般的TBM数据采集频率为0.2Hz,即每5s就有TBM参数写入传感器。以此采集频率来计算采集50个数据大约需要100s,TBM大约掘进4～10.5cm,说明人为创建的24种地质突变类型在较短距离内围岩等级就会发生改变。这些地质突变条件已经属于较复杂的地质环境,而BiLSTM-SVR模型仍有如此高的预测准确度和鲁棒性,证明此模型可以为TBM智能化施工提供一定的参考。

3 结 语

a.BiLSTM-SVR模型预测24种组合类型的围岩等级的准确度较高,预测结果的RMSE均小于0.0265、MAPE均小于0.95%,MAE均小于0.0160。测试样本为低围岩等级的预测准确度比高围岩等级高。当预测围岩等级的训练集数据信息较复杂以及组合类型是间隔突变时会导致BiLSTM-SVR模型的预测结果存在过拟合现象,导致预测准确度变低。

b.BiLSTM-SVR模型的推力和扭矩的预测准确度最高,净掘进速度和开挖比能的预测准确度最低。净掘进速度和开挖比能受不良地质环境的影响较大,它们的岩机相互作用规律较难充分挖掘。BiLSTM-SVR模型各掘进参数的R2平均值均大于0.8715、RMSE平均值均小于0.1722、MAPE平均值均小于0.5%、MAE平均值均小于0.1324。

c.BiLSTM-SVR模型比单一BiLSTM模型和SVR模型的拟合优度平均提高了6.53%,均方根误差平均降低了41.96%,平均绝对百分比误差平均降低了40.60%,平均绝对误差平均降低了0.4101。BiLSTM-SVR模型预测掘进参数时的预测准确度和鲁棒性高于单一的BiLSTM模型和SVR模型,即进行单一模型的组合可以有效地提高预测模型的准确度和鲁棒性。

d.本文构建的BiLSTM-SVR模型具有较高的预测准确度和鲁棒性,如果TBM场景和参数信息有较大改变,该模型的通用性依然能够得到保障。开挖比能的大小对规划工期和预估施工成本具有重要的指导意义,提高开挖比能预测精度是下一步工作的重点。由于验证BiLSTM-SVR模型在地质突变条件下预测准确度的数据集有限,所以还需进一步通过大量工程数据验证该预测模型的泛化性。