基于水光电力系统时序生产模拟模型的水光优化配比研究
2024-01-23李继清
李继清,龙 健,刘 洋
(1.华北电力大学水利与水电工程学院,北京 102206; 2.华北电力大学苏州研究院,江苏 苏州 215123;3.华能澜沧江水电股份有限公司,云南 昆明 650214)
高比例新能源的接入使电力系统的运行变得更为复杂,新能源的波动性[1-2]、间歇性[3-4]也使得电力的实时平衡变得困难,导致新能源弃电现象频现,风光资源浪费严重[5-6]。因此,充分发挥各种能源互补的特性,建立基于水电调节的多能互补系统,科学评估系统的新能源消纳能力,优化各种新能源之间的互补容量配比,对于降低新能源弃电率和含新能源电力系统的规划、发展具有重要的指导意义[7-9]。
目前,新能源消纳能力常用的分析方法主要有典型日法、随机生产模拟法、时序生产模拟法。基于典型日法[10-11]提出的调度方式得到的结果是最严重情况下的新能源平衡情况,计算结果过于保守,不利于提高新能源实际上网电力电量;随机生产模拟法[12-13]中的新能源出力和负荷采用服从某种分布的数据,无法模拟机组组合情况,忽略了与时序相关的约束,无法全面分析生产成本;时序生产模拟法[14-16]是指在给定的负荷条件下模拟各发电机组的运行状况,并计算发电系统生产费用的一种时序仿真方法。该方法的优点是能够考虑系统负荷、新能源发电出力等的时序变化特性,更适用于指导新能源的规划问题。耿路等[17]基于时序生产模拟法分析了不同负荷增长率和不同新能源接入方式下张家湾地区新能源消纳能力;葛毅等[18]将负荷划分为居民负荷和工业负荷,以经济性为目标对我国东部某省电力系统进行了时序生产模拟,得到了不同负荷的优化配比;王琨玥[19]通过考虑光伏出力与城市负荷的时序关系,并结合火电机组的调频限制,建立了一种基于时序生产模拟的光伏容量规划模型。另一方面,新能源互补容量配置的相关研究仍局限于优化互补系统的运行效率或效益,而较少研究配置方案是否利于系统稳定可靠、调度灵活性及社会发展效益等[20]。刘军涛等[21]通过分析青海省海南州各类可再生能源资源禀赋、开发条件等因素,提出了一套水风光储多能互补基地电源配置方案;申建建等[22]构建了灵活性裕量期望最大和不足期望最小模型,动态适应不同新能源接入比例、风光装机比例等场景下的水风光互补调度需求。准确量化不确定性新能源容量配比是研究以新能源为主的多能互补系统优化调度的基础[23-25],对我国电网安全、稳定和清洁能源消纳具有重要意义。
因此,本文建立计及水电站丰枯期出力波动、光伏电站日夜出力间歇性及需求端负荷变化的时序生产模拟模型,模拟产生多种不同的水光容量配比方案,并从水光系统结构性、经济性、灵活性和可靠性方面综合优选水光最优容量配比,通过金沙江上游川藏段(以下简称“川藏段”)水光互补容量优选验证模型的合理性,以期为低碳电力要求下的网源协调规划提供参考。
1 水光电力系统时序生产模拟模型
1.1 水光互补特性分析
基于出力曲线的定性分析法主要是通过绘制水电站、光伏电站同一时间尺度的出力曲线,通过观察水电站、光伏电站出力曲线峰、谷出现时间,进而定性判断水光出力的时间互补性。定量分析水光互补特性主要是借助相关分析法研究梯级水电站单独运行、联合运行条件下与光伏电站出力的相关性。较为常用的相关系数有Pearson简单相关系数、Spearman等级相关系数和Kendall相关系数。相关系数为负值,则表示随机变量之间呈负相关关系,即两者呈相反的变化趋势,互补性较好;反之亦然。一般认为,相关系数的绝对值在0~<0.33范围内时两者之间为弱相关,0.33~<0.67为中等相关,0.67~<1为强相关。
1.2 模型构建
1.2.1 目标函数
为尽量减少整个系统的投资费用、运维费用等成本,增加系统的经济性收益。水光发电系统的时序生产模拟模型以投资经济性最优为目标函数,即在满足约束条件的情况下,配置合适的光伏发电系统容量,使整个工程周期内投资收益最大[26]。引入净现值计算水光互补电站运营周期总利润,建立目标函数:
(1)
其中I(Sp)=Ep(Sp)Pp(Sp)+EhPhC(Sp)=Ccp(Sp)+Cch+Cop(Sp)+Coh
式中:Sp为光伏电站容量;n为运营周期;i为基准收益率;Ccp、Cch分别为光伏电站、水电站建设成本,包括折旧费及建设贷款偿还等;Cop、Coh分别为光伏电站、水电站经营成本;Pp、Ph分别为光伏发电和水电电价;Ep、Eh分别为光伏电站、水电站年发电量;j表示第j台机组;Nj、Nk分别为参与优化的光伏、水电机组的台数;T为优化时间总长度;Yj为二进制变量,表示机组j启动状态,1表示正在启动,0表示不在启动状态;Zk为二进制变量,表示机组k停机状态,1表示正在停机,0表示不在停机状态;Pj,t、Pk,t为光伏机组j、水电机组k在t时段的出力。
1.2.2 约束条件
a.电网负荷约束。电网负荷约束主要包括电力平衡、电量平衡约束:
(2)
Es=Ep(Sp)+Eh
(3)
式中:Ns,t为受端电网负荷需求;Es为受端电网发电量需求。
b.水电站运行约束。 水电站运行约束包括水电站水量平衡约束(式(4))、库容曲线约束(式(5))、库水位约束(式(6))、下游水位流量关系约束(式(7))、水电站水头约束(式(8))、水电站出力限制(式(9))、水电站最大过流能力限制(式(10))、机组爬坡率约束(式(11))。
Vt+1=Vt+(Qrk,t-Qfd,t-Qqs,t)ΔTt
(4)
Zsy,t+1=fZV(Vt+1)
(5)
Zsy,min≤Zsy,t+1≤Zsy,max
(6)
Zxy,t=fZQ(Qck,t)
(7)
(8)
Xj,tPmin,t≤Pj,t≤Xj,tPmax,t
(9)
Qfd,t≤Qfd,t,max
(10)
(11)
式中:Vt、Vt+1分别为t时段初、末库蓄水量;Qrk,t、Qfd,t、Qqs,t分别为t时段平均入库流量、出库流量和弃水流量;ΔT为一个时间步长;Zsy,t+1为t时段末水电站上游水位;fZV(·)为库容曲线函数;Zsy,min、Zsy,max分别为t时段末水电站上游允许最低、最高水位;Zxy,t为t时段下游平均水位;fZQ(·)为下游水位流量关系函数;Qck,t为出库流量;H为净水头;ΔHt为水电站t时段水头损失;fΔH(·)为水电站水头损失函数;Pmin,t、Pmax,t分别为t时段的最小、最大出力;Xj,t为二进制变量,表示机组j运行状态,1表示正在运行,0表示不在运行状态;Pj,max为机组j的最大出力;Dp、Dn分别为系统正、负旋转备用;CN,t为光伏发电站t时段的可信容量。除了上述约束,所有变量还必须为非负值。
c.光伏电站运行约束:
(12)
式中Np,t为光伏电站t时段的预测出力。当互补光伏电站出力超出最大出力Npmax时,需要弃掉出力Npl,t。
d.系统约束。送出通道容量限制、旋转备用约束分别为
(13)
(14)
式中:Nmax为系统送出通道容量,取为800万kW;Nt为t时段送出通道的送出电力。
1.3 模型求解
采用分支定界法对水光电力系统时序生产模拟模型进行求解。分支定界法屏蔽了解空间中明显不利于目标函数最优化的解,使整个计算过程更趋向于有最优解的分支,并针对可行分支计算了限值,减少了可选解的范围。分支定界法求解步骤主要包括分支、松弛与定界3个步骤[27]。常用的分支定界法求解器主要有GUROBI、CPLEX和IPSOLVE等,其中的IPSOLVE求解器具有计算迅速、设备兼容性好等优点,应用广泛[28],因此本文采用IPSOLVE求解器对时序生产模拟模型进行求解。
1.4 水光容量配比方案优选
基于水光电力系统时序生产模拟模型产生的水光容量配比方案,从系统结构性、经济性、灵活性和可靠性4个方面综合评价,择优选取最佳的水光容量配比方案。对于系统结构性,基于受端电网年负荷、典型日负荷特性和送端电源特性,通过拟定直流曲线分析。具体的评价指标主要有水光容量比、水光电量比、弃水率、弃光率及等效弃光率。
经济性通过对系统进行投资效益及电价竞争力分析,具体的评价指标主要有综合上网电价、落地电价及光伏资本金内部收益率。综合上网电价P综根据水光利用情况按电量加权计算(式(15))。综合上网电价加上输电价P输(含直流输电价和送端配套加价)即为落地电价P落(式(16)),落地电价越低,其在受端的电价竞争力越强,越有利于水光打捆外送。光伏资本金内部收益率根据受端落地电价,扣除输电价,反推送端光伏电价需求以及相应的光伏投资内部收益率,得到不同单位造价成本下的光伏投资内部收益率。
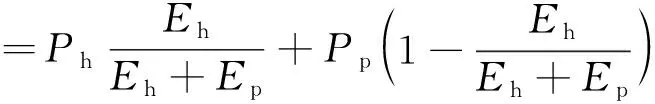
(15)
P落=P综+P输
(16)
水光系统灵活性与可靠性评价基于水光互补系统时序生产模拟模型,分别采用水光联合调节难度、受端调峰压力[22]和直流送电波动、送端电力富余定性评价,并结合结构性、经济性评价指标,综合择优选取最佳的水光容量配比。模型构建技术路线见图1。

图1 模型构建技术路线Fig.1 Technology roadmap of model construction
2 模型验证
2.1 研究区概况
金沙江玉树(巴塘河口)至石鼓河段称为金沙江上游段,全长772 km,天然落差约1516 m,水能资源丰富。根据金沙江上游“一库13级”的梯级布局,在川藏段规划布置岗托、岩比(开发存在较大不确定性,暂不考虑)、波罗、叶巴滩、拉哇、巴塘、苏洼龙、昌波8个梯级,初拟装机容量956万kW,2030年除岩比外七级水电站全部建成投产,各水电站投产时序、位置分别见表1、图2。

表1 金沙江上游川藏界河段梯级水电站投产时序Table 1 Time sequence of putting into operation of cascade power station in Sichuan-Tibet boundary of the upper reaches of Jinsha River 单位:万kW

图2 川藏段水电站位置Fig.2 Location map of hydropower stations in Sichuan-Tibet boundary
川藏段太阳能资源丰富[29-32],以太阳总辐射年辐照量为指标,按照《太阳能资源等级总辐射》分级标准,川藏段太阳能资源等级多为B级(资源很丰富区),年总辐射量基本都在6000MJ/m2以上,具备较大开发价值,初步规选光伏装机约3500万kW,其中西藏侧约3000万kW。
2.2 川藏段水光互补特性分析
2.2.1 水电站出力特性分析
金沙江上游丰、平及枯水期分别为6—10月、5月和11月、12月至翌年4月,选取远景年2030年,绘制平水年川藏段各水电站单独运行、联合运行的出力特性曲线,如图3所示。
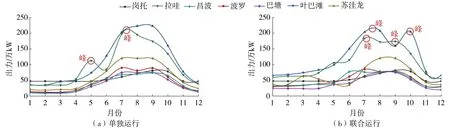
图3 川藏段梯级水电站群出力特性Fig.3 Output characteristics of cascade hydropower stations in Sichuan-Tibet boundary
由图3可知,川藏段七级水电站2030年(平水年)单独运行时,7—9月出力较其他月大,拉哇水电站的出力呈现“两峰一谷”的特点,分别于5月、7月达到峰值,出力分别为112.7万kW、198.6万kW;联合运行时,叶巴滩、苏洼龙水电站出力呈现出“两峰一谷”的特性,分别于8月、10月和3月、9月达到峰值;昌波水电站出力峰值有所提前,由7月份提前到6月,出力为77万kW;梯级水电站联合运行年发电量为429亿kW·h,较单独运行时多41亿kW·h,丰平枯期发电量比例分别约为60%∶13%∶27%,枯水期发电量占比提高了9%,年利用小时数约为4697,较单独运行时提高了450h。
对于月内、日内梯级水电站出力特性,川藏段梯级水电站调节能力较强,各水电站日内出力可在最小出力与预想出力之间根据电网负荷、光伏发电等进行调节,满足电网负荷需求,保证系统安全稳定运行。
2.2.2 光伏电站出力特性分析
基于川藏段周边江达、贡觉、德格及巴塘等六县的测光数据,并结合当地气象数据,得到光伏电站全年8760h出力曲线。对于年内出力特性,光伏电站出力存在一定季节性差异,各月平均出力系数在0.14~0.22之间,月际变化较为明显,呈现冬春季大、夏秋季小的特点。
由图4可知,光伏电站日内出力趋势较为一致,主要受昼夜影响大,出力一般12:00—14:00达到峰值,20:00至次日6:00出力为0;春、秋及冬季出力均于13:00达到峰值,夏季出力出现2个峰值,分别于12:00、14:00达到出力峰值。最小日光伏电站出力时段为7:00—19:00,于10:00、13:00达到峰值,12:00达到出力低谷,呈现出“两峰一谷”的特点。光伏电站出力随昼夜变化较大,具有间歇性。从保证出力和累计电量特性来看,光伏出力保证率水平较低,但电量累计效应明显。随着昼夜、季节及天气等变化,光伏出力具有间歇性、波动性和随机性特点。

图4 光伏电站出力特性曲线Fig.4 Output characteristics curve of photovoltaic power station
2.2.3 水光互补特性分析
对于年内水光互补特性,光伏电站与水电站单独运行、联合运行的出力过程及出力相关系数分别如图5、表2所示。

表2 平水年梯级水电站单独、联合运行时水光年内出力相关系数Table 2 Annual water-light output correlation coefficient of cascade hydropower station in normal water years when it is operated independently and jointly with photovoltaic power station
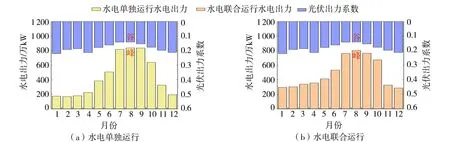
图5 金沙江上游水电与光伏电站年内出力Fig.5 Annual output of hydropower station and photovoltaic power station in the upper reaches of Jinsha River
从图5可知,光伏电站、水电站的年内各月出力均呈现出“一峰一谷”形式,光伏电站的年内各月差异较水电小,光伏电站于12—2月达到发电高峰,7—9月达到低谷;而水电站于7—9月达到高峰,12—2月达到低谷;水电站出力于8月达到最高峰,而对应的光伏电站出力达到最小值。光伏出力的峰、谷与水电出力的谷、峰在时间上对应,水电、光电的出力存在年内互补特性。由表2可知,川藏段梯级水电站无论是单独运行还是联合运行,其与光伏电站的出力均具有显著的负相关,具有较强的互补特性。
对于日内互补特性,川藏段水电站具备一定的调节能力,可根据系统负荷变化情况进行日调节,日间光伏发电时段,通过加大水电站蓄水降低水电出力,用光伏电量“置换”水电电量;夜间或光伏少发时段,通过释放水电站水量抬高水电工作位置,水光日内互补后水光系统整体出力趋于平滑[33]。
2.3 川藏段水光优化配比研究
2.3.1 水光容量配比方案
基于构建的时序生产模拟模型,考虑受端湖北电网负荷特性、直流送电通道及送端水电留存,模拟产生多个川藏段水光互补配比方案。根据湖北电网历史负荷曲线,对2030年负荷进行预测,湖北省2030年负荷呈W形,1—8月、9—12月最大负荷呈现“高-低-高”的V形变化趋势。由图6可知,日负荷特性呈现午、晚2个高峰。夏季负荷高峰出现在15:00和21:00,冬季负荷高峰出现在11:00和19:00,负荷低谷出现在5:00左右。
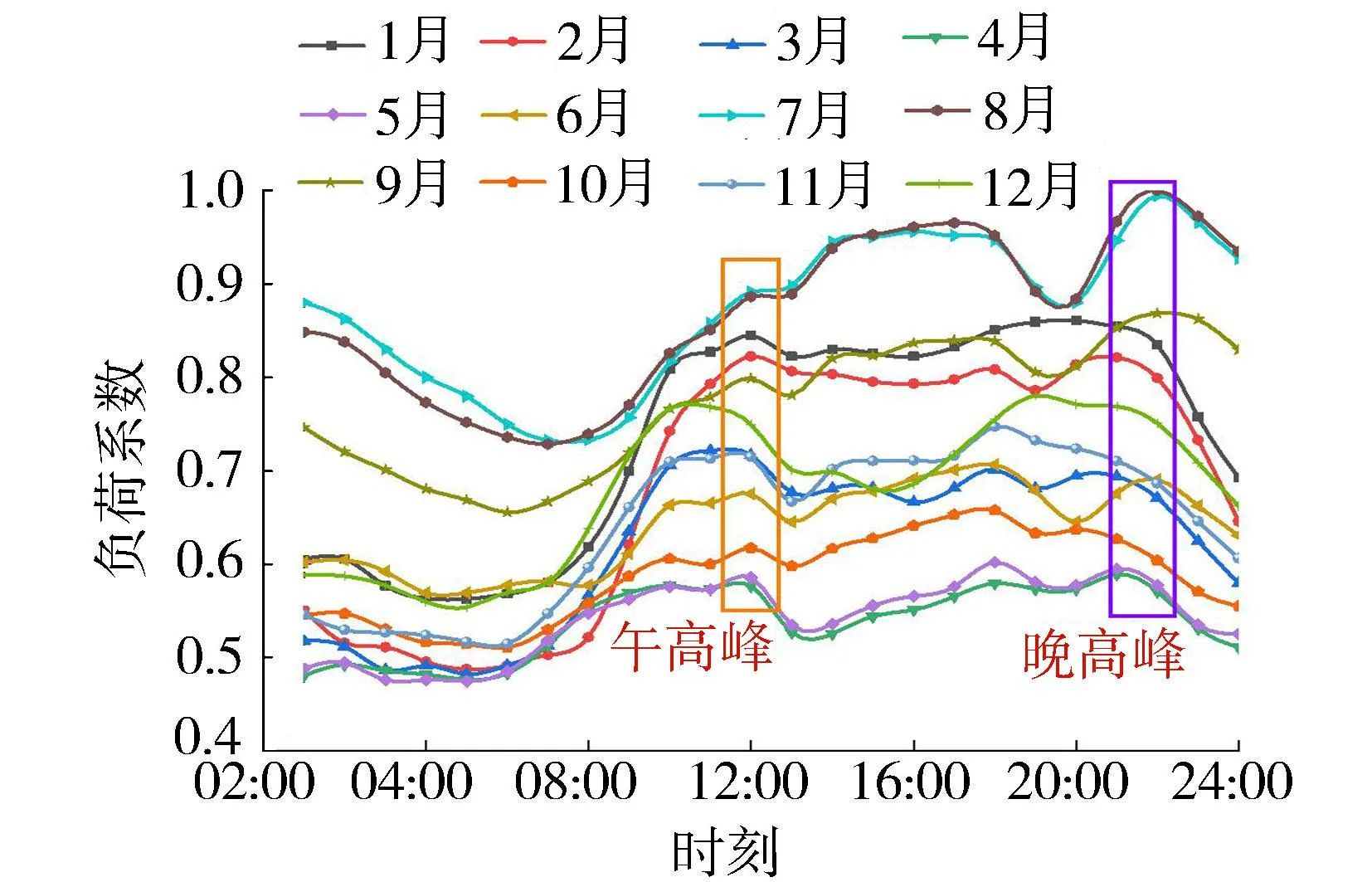
图6 湖北电网典型日负荷特性Fig.6 Typical daily load characteristics of Hubei power grid
2030年金沙江上游水电全部投产之后,水电按913.6万kW考虑,结合四川、西藏电网供需形势及受端湖北用电需求,川藏段水电留存电量暂按考虑枯期(1—4月、12月)留存本地30%,四川、西藏按1∶1分配,拟定水电不留存和水电枯期留存两类方案,时序生产模拟后求解得到的各方案水光配比容量如表3所示,其中设置水电枯期留存30%中的B1方案用于分析进一步增加光伏电站装机容量时各指标变化情况。

表3 水光容量配比方案Table 3 Water and light complementary ratio schemes
2.3.2 水光容量配比方案选取
2.3.2.1 系统结构性
2030年,配套水电装机913.6万kW、年发电量423亿kW·h,其中枯期留存34亿kW·h。由图7(a)可知,打捆外送规模400万kW光伏时,7—9月最大电力为800万kW,不调峰;12—2月最大电力约640万kW,其他时段最大电力800万kW,调峰范围为0.1~0.7 pu。直流曲线年送电量447亿kW·h,其中丰、平、枯电量占比为61%∶15%∶24%,直流利用小时数为5465,弃光率2%,考虑不弃水的折算值,等效弃光率5%。打捆外送规模500万kW光伏时,直流曲线如图7(b)所示,直流利用小时数为5500,水电站发生弃水,弃水率2%,弃光率9%。打捆外送规模600万kW光伏时,直流曲线如图7(c)所示,直流利用小时数为5912,水电站弃水率1%,弃光率3%。当打捆外送规模700万kW光伏时,如图7(d)所示,7—9月最大电力与调峰范围与打捆外送400万kW光伏时相同;12—2月最大电力约640万kW,其他时段最大电力800万kW,调峰范围0.1~0.5 pu。直流曲线年送电量488亿kW·h,直流利用小时数约为6000,弃光率8%,由于金沙江上游水电丰期电量较大,可调空间有限,导致进一步增加打捆光伏规模后等效弃光率将增加至15.4%,弃光电量增加17亿kW·h。
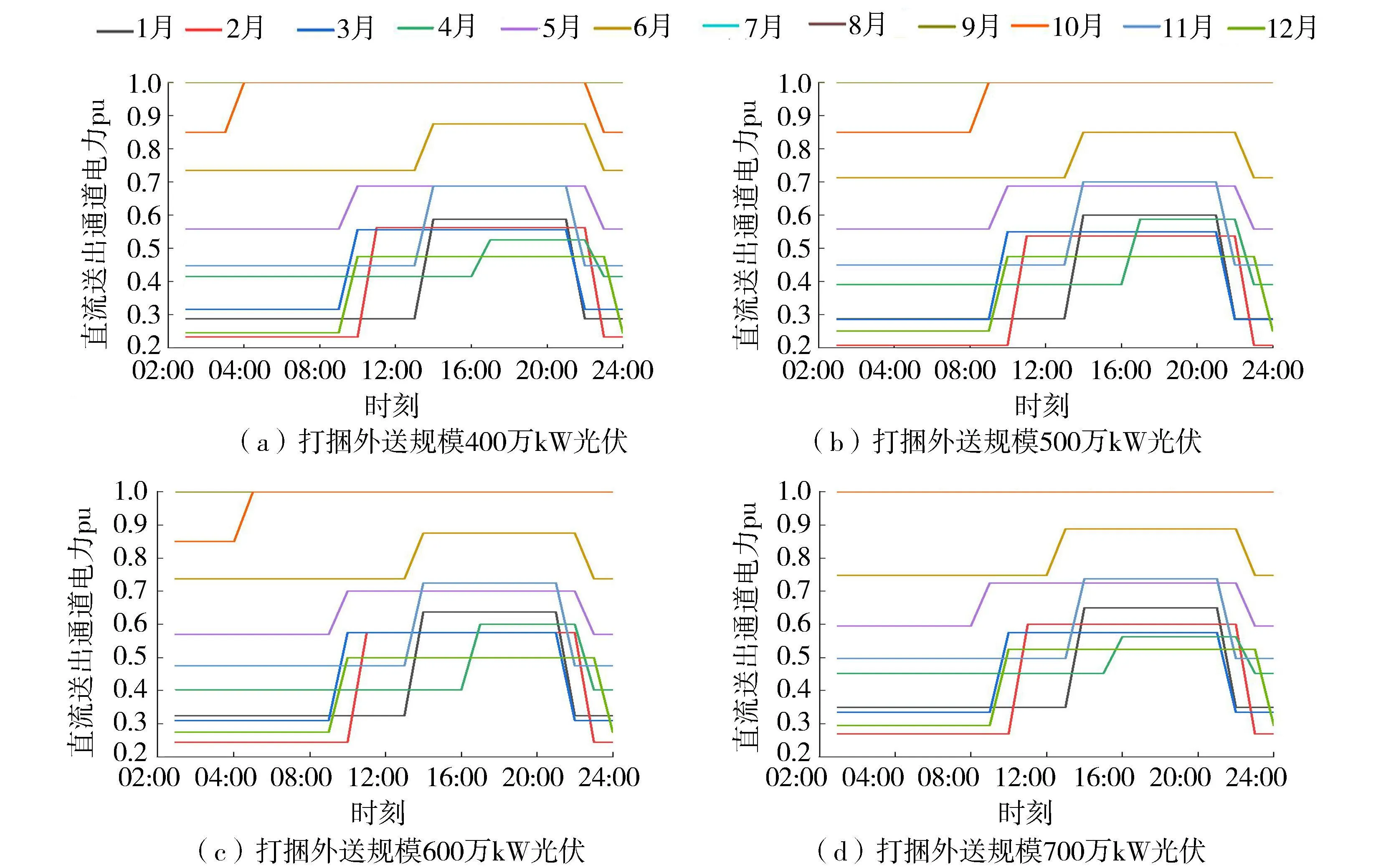
图7 直流典型日送电曲线Fig.7 Typical daily DC transmission curve
2.3.2.2 经济性
对于各水光配比方案,根据受端电价不高于湖北基准电价上浮10%,扣除输电价(含送端配套0.03元/(kW·h))后,考虑光伏项目单位造价4200、4500元/kW,反推送端光伏电价需求以及相应的光伏投资内部收益率。B1、B2方案配套光伏600万、700万kW情况下,送端光伏电价分别为0.286、0.271元/(kW·h)时,光伏资本金内部收益率5.7%~9.5%;而其他方案光伏内部收益率均低于2.0%。
由表4所示,A类方案综合上网电价相差不大;水电枯期留存30%的B类方案,直流利用小时数为6000,配套600万、700万kW光伏的方案综合上网电价较其他方案明显具有一定优势,其中B1方案较单独输送水电降低约0.025元/(kW·h);当直流利用小时数控制在5500水平,配套光伏400万~500万kW,综合上网电价相差不大。

表4 直流输电价及落地电价分析Table 4 Analysis of DC transmission price and landing price 单位:元/(kW·h)
对于落地电价,仅输送梯级水电时,落地电价为0.512元/(kW·h),配套打捆一定规模光伏的各种方案,落地电价与仅输送水电相比降低约0.021~0.033元/(kW·h)。其中B类方案中,直流利用小时数在6000水平,配套600万~700万kW光伏,受端电价竞争力相对较强。
2.3.2.3 灵活性与可靠性
对于水光系统灵活性而言,打捆的光伏容量越大,光伏电站的波动性、随机性越大,水光系统联合调节难度也越大,进而导致送出电力的波动性也就越大,造成受端调峰压力越大。因此,考虑枯期水电留存配套700万kW光伏的B1方案系统联合调节难度、受端调峰压力最大,随着配套光伏的容量越来越小,其联合调节、受端调峰压力也越来越小。A类方案也呈现相似的变化规律。
对于系统可靠性而言,打捆配套的光伏容量越大,光伏电站发电量也就越大,水电全投后其送端电力富余越大。对于B类方案,因枯期本就留存一部分电力,其电力富余比相同打捆容量下的A类方案更大,B1方案电力富余最大,A1方案送端电力富余最小。
2.3.2.4 综合比较及光伏配套规模建议
综合考虑外送通道合理利用水平、弃电率、投资效益、电价竞争力等因素,从结构性、灵活性、可靠性及经济性方面分析多个组合方案,其评价结果详见表5。由表5可知,直流利用小时数为5500~6000,A类方案整体较B类方案电价竞争力差,且弃光率、弃水率较高,资源浪费严重。B类方案中,B1方案经济性最优,综合上网电价为0.380元/(kW·h);B2方案电价竞争力差于B1,系统灵活性、可靠性增强;B4方案较B1方案综合上网电价高0.008元/(kW·h),但系统结构性、灵活性及可靠性明显提高。
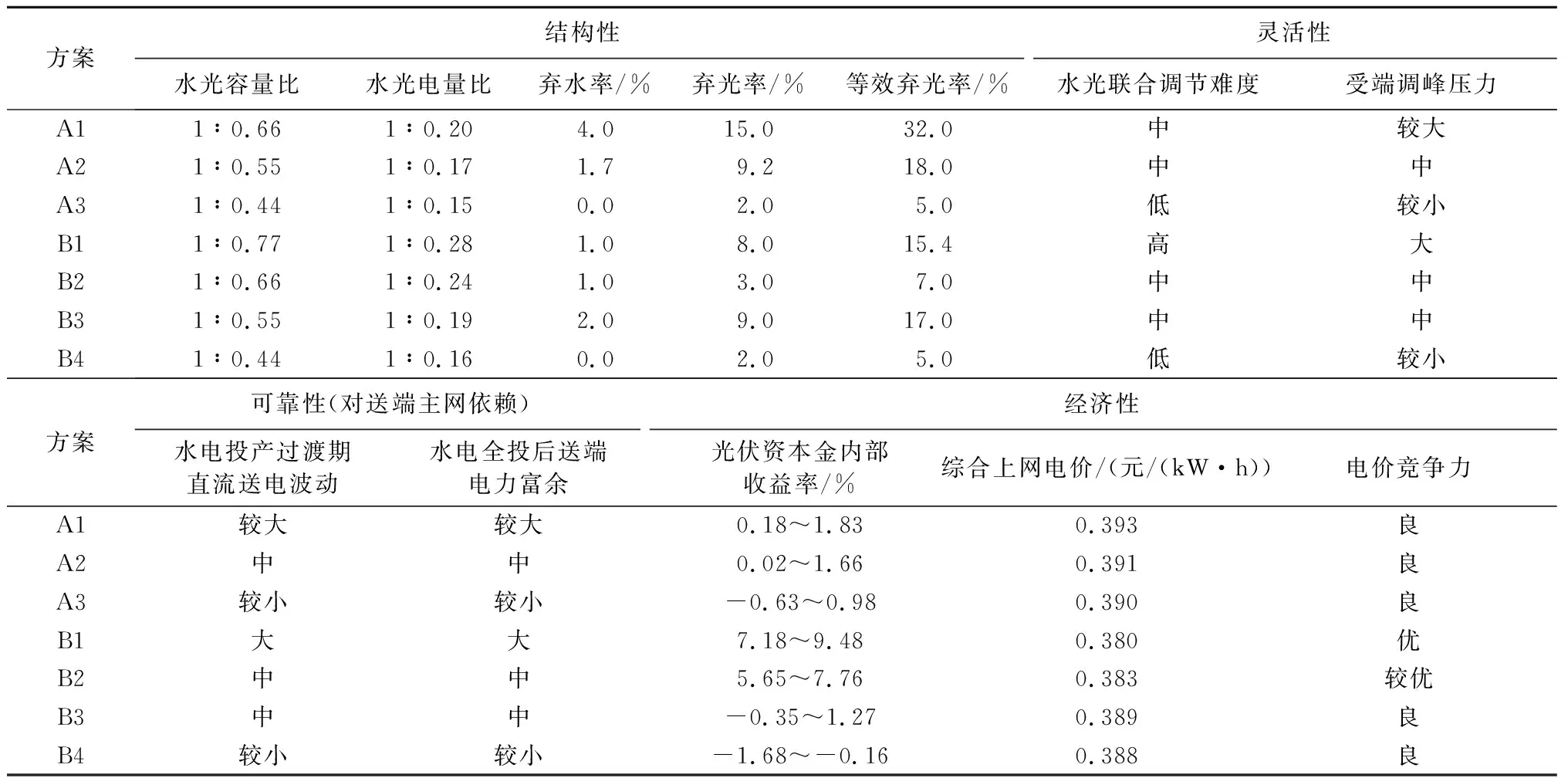
表5 水光容量配比方案综合比较Table 5 Comprehensive comparison table of water and light complementary ratio schemes
综上,推荐B4方案,新增非水可再生电量约60亿kW·h,占受端湖北全社会用电量比例约为1.7%~2%。若考虑湖北省具备调峰能力的情况下,配套光伏规模可进一步适当提高至600万~700万kW。与此同时,需要进一步加强水电站与光伏电站联合运行的安全性,避免水电站因调峰而长期在不稳定区运行。
3 结 语
本文针对新型电力系统下新能源的消纳问题,考虑系统负荷、新能源出力的时序性,建立了水光电力系统时序生产模拟模型,并从系统结构性、灵活性、可靠性及经济性等方面对方案进行评价,综合确定水光容量配比,最后通过金沙江上游川藏段水光发电系统验证了模型合理性。金沙江上游川藏段光伏电站与水电站出力具有较好的年内、日内互补特性;A类方案整体较B类方案电价竞争力差,且弃光率、弃水率较高,资源浪费严重;B类方案中,B1方案经济性最优,但综合考虑结构性、灵活性和可靠性,B4方案整体更好,其新增非水可再生电量约60亿kW·h,占湖北全社会用电量比例约为1.7%~2.0%。
