考虑干缩裂隙动态变化的优势流入渗模型
2024-01-23程实,陈瑾,罗易
程 实,陈 瑾,罗 易
(1.湖北经济学院工程管理系,湖北 武汉 430074;2.湖北经济学院碳排放权交易省部共建协同创新中心,湖北 武汉 430074;3.湖北省地质实验测试中心,湖北 武汉 430074; 4.中国地质大学(武汉),湖北 武汉 430074)
自然界中,土体因失水收缩产生表面裂缝的现象十分普遍,对于含亲水性矿物(伊利石、蒙脱石)较多的裂土,这种现象尤为突出[1-3]。干缩裂隙的产生为雨水入渗提供优势通道,导致大量雨水绕过土体基质进入裂隙底部,形成优势流[4-5]。优势流使雨水快速入渗至土体深部,是造成地下水污染[6]、水资源流失[7]及边坡失稳破坏[8-9]的重要影响因素。
为模拟雨水在裂土中的运移过程,Chen等[10-11]基于双孔隙域理论建立了优势流入渗模型。此类模型将土体孔隙分为大孔隙(常指植物根孔、生物孔洞及天然裂缝,本文特指裂隙域)与小孔隙域(常指土体基质域),认为入渗只发生在大孔隙域内(如干缩裂隙)。然后,诸多学者利用Richard方程[12]或Green-Ampt入渗模型[13]、Poiseuille方程[14]、运动波方程[13]等描述大孔隙域内的水体流动特征。然而,大量试验表明[7,15-17],雨水在裂土中的入渗同时发生在基质域与裂隙域内,雨水只在裂隙域内入渗的假设与真实情况不符。为此,Gerke等[18]基于Richard方程提出了双重渗透模型,可模拟雨水在大孔隙与小孔隙域内的入渗过程。该模型因具有明确的物理意义得到了广泛使用。Larsbo等[19-20]将其改进后用于模拟裂土的水分运移过程。其中大多数研究均假定土体基质域与裂隙域的孔隙体积及孔隙分布特征保持不变。然而,裂土中的孔隙系统往往随着含水率变化而动态变化,导致雨水入渗过程十分复杂。例如,干缩裂隙在降雨入渗过程中随含水率的增加会逐渐闭合,Favre等[21-22]认为裂隙闭合会显著降低土体渗透性,甚至使优势流现象消失。因此,静态的双域入渗模型难以用于预测干缩裂隙中产生的优势流。Liu等[23]将两域的孔隙体积变化作为土体收缩指标的函数,考虑了裂隙动态变化对入渗过程的影响,但其提出的函数关系不仅缺乏物理一致性,还包含大量难以确定的参数,导致模型存在等效性问题。此外,上述模型均基于Richard方程,存在较为明显的数值收敛问题。
Green-Ampt入渗模型因其物理意义明确、形式简单而被广泛应用于一维均质入渗问题的研究中。该模型可预测积水时间、累积入渗量及湿润锋深度等水文参数,对研究地表径流、评价灌溉效率及边坡稳定性具有重要意义。然而,目前仅有少量学者将Green-Ampt入渗模型[24-26]用于模拟裂土中的优势流,但同样未考虑干缩裂隙的动态变化。Stewart等[26]虽然考虑了干缩裂隙的动态变化,但其参数过多且仅适用于裂隙发育程度较低的情况。此外,不论是基于Richard方程还是Green-Ampt入渗模型,在模拟裂土中的优势流时,均将裂隙域作为透水材料处理,赋予其水力学参数,如渗透系数或单位水力梯度。然而,裂隙的水力学参数不能通过试验测得,其水力梯度也常远大于单位梯度,经验赋值或反算法不仅带来了误差,还严重削弱了模型的预测能力。
为此,本文基于双孔隙域入渗理论,结合Green-Ampt入渗模型,提出了可考虑干缩裂隙动态变化的优势流入渗模型,探讨了降雨强度、裂隙初始面积率及裂隙深度对土体两域积水时间、优势流入渗量及入渗深度的影响规律。
1 优势流概念模型
如图1(a)(b)所示(图中β为裂隙面积率),将土体中多条干缩裂隙按照等效面积与体积视为单个裂隙域,裂隙两侧和底部的土体基质分别划分为L基质域、B基质域。降雨过程中(定雨强),由于土体基质吸水膨胀,裂隙域与B基质域的体积将会减小。本文假设:①裂隙深度不变,土体表面的沉降忽略不计,则各域的体积与其表面积成比例变化,如图1(c)所示;②雨水仅在竖直方向运移,不考虑通过裂隙壁在L基质域与裂隙域之间的水分交换;③土体基质域的饱和渗透系数远小于裂隙域,则降雨时基质域表面将先于裂隙域积水(裂隙域积水指裂隙空间被雨水填满)。将基质域与裂隙域的积水时间分别表示为tp,m与tp,c。当降雨强度大于基质域饱和渗透系数时,考虑上述假设可将入渗过程分为3个阶段:

图1 裂土优势流建模过程示意图Fig.1 Modeling process of preferential flow in cracked soil
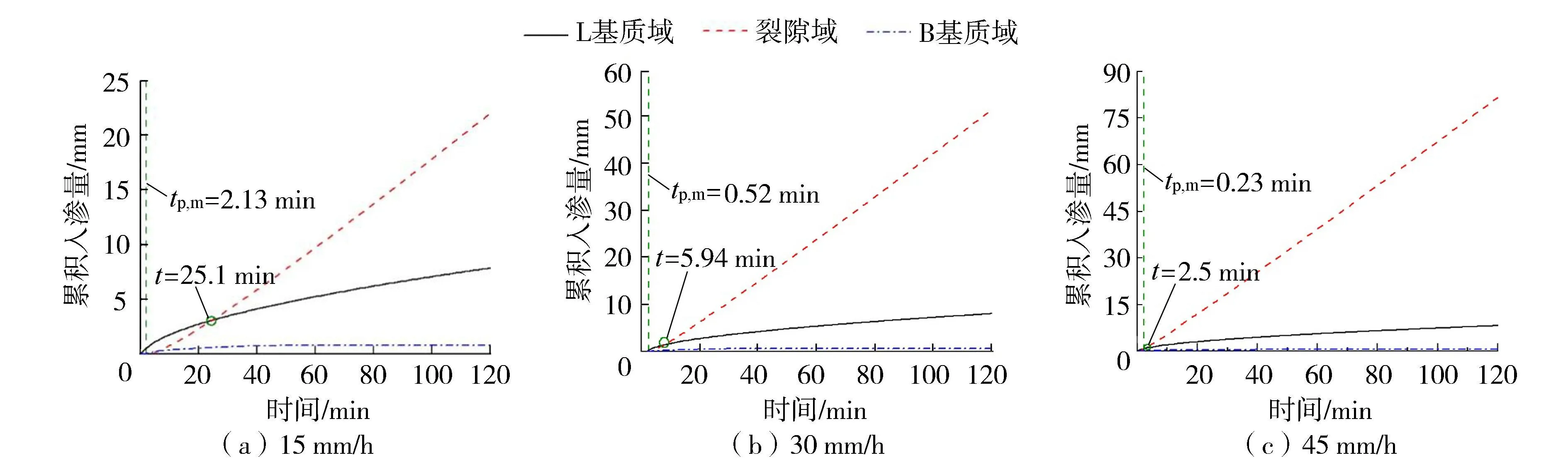
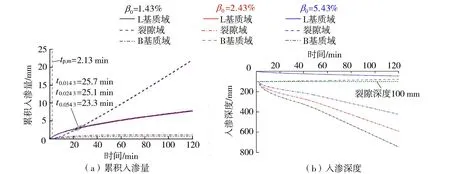
a.基质域积水前,t b.裂隙域积水前,基质域积水后,tp,m≤t c.裂隙域积水后,t≥tp,c。裂隙域被雨水填满后,B基质域内的入渗由定水头边界条件下的Green-Ampt模型求解。 此外,基于大量土体干缩裂隙发展演化规律室内试验成果,在上述过程中引入裂隙面积率、质量含水率与时间之间的经验函数,考虑了干缩裂隙动态变化对入渗过程的影响。 裂土的总入渗速率定义为[18] (1) 式中:itotal为总入渗速率;Q为水通量,下标m和c分别代表基质域与裂隙域;A为表面积;i为入渗率;β为裂隙域的体积权重系数,本文中与裂隙面积率相等。 将基质域内的入渗视为活塞流(Green-Ampt入渗模型中的假定)并对式(1)应用Darcy定律可得: (2) 式中:Ktotal为裂土的整体饱和渗透系数;dψ/dz为竖向水力梯度;Km为土体基质的饱和渗透系数(包括L与B基质域)。 需要说明的是,以往的双孔隙域渗透模型也将式(2)右端第2项裂隙域中的入渗过程视为活塞流,然后为裂隙赋水力学参数并应用Darcy定律。考虑裂隙为容水空间而非透水性材料,Darcy定律不适用于雨水在裂隙中的运移过程,因此本文式(2)中只给出裂隙域的渗透速率广义表达式。 根据Green-Ampt入渗方程解,可得水力梯度的表达式为 (3) 其中zw=I/nn=θs-θ0 式中:h0为土体表面积水深度;sf为湿润锋处土体基质吸力水头;zw为湿润锋深度;I为累积入渗量;n为容水孔隙体积率;θs、θ0分别为土体的饱和与初始体积含水率。 根据累积入渗量与入渗速率的导数关系,联立式(2)与式(3)得湿润等深度与时间的关系: (4) 裂隙面积率变化是本文考虑干缩裂隙动态变化的核心思想。大量室内外裂隙发展演化规律试验结果[8-9]表明干缩裂隙形成时,裂隙面积率与表层土体质量含水率具有良好的线性关系,即: β=aw+b (5) 式中:a、b为拟合参数,可通过裂隙面积率与含水率曲线得到[7];w为质量含水率。当认为土体胀缩为一可逆过程时,式(5)可用于描述降雨过程中裂隙的闭合规律。 降雨过程中w随时间的变化曲线可通过现场实测得到。为便于后续模型的敏感性分析,本文基于室内不同降雨强度下得到的土柱表层质量含水率测试结果,采用Boltzmann生长模型描述含水率增长过程: (6) 式中:ws为土体饱和质量含水率;w0为初始质量含水率;tmid为含水率达到w=(w0+wmax)/2的时间;tcon为拟合参数。需要说明的是,此处选用Boltzmann生长模型不仅是因为其与测试数据的拟合程度较高,还考虑到该模型有较为清楚的物理意义,与定雨强条件下表层土体质量含水率的增长过程相符。 将式(6)代入式(5)可得: (7) 2.2.1 入渗方程(t 当t (8) (9) 式中:r为降雨强度;AL-m为L基质域表面积。 各域的累积入渗量为 (10) (11) 2.2.2 入渗方程(tp,m≤t 当tp,m≤t (12) 式中:λ为常数,常取为2/3;sf,m为土体基质域中湿润锋处的基质吸力水头;nm为基质域的容水孔隙体积率。 令C=Km/nmsf,m,联立式(8)与式(12)可得tp,m的隐式表达式: (13) tp,m确定后,L基质域内的累积入渗量可表示为 (14) 将式(10)、式(12)代入式(14)可得: (15) 对于裂隙域,在其未被雨水填满之前,入渗速率可由降雨强度与L基质域的入渗速率之差求得: ic=r-iL-m (16) 相应的裂隙域累积入渗量为 (17) 为确定裂隙域的积水时间,现对B基质域的雨水入渗过程进行分析。B基质域在积水前,其入渗速率和入渗量与裂隙域相等,仍可由式(9)(11)求得。当积水开始出现在B基质域表面时,由式(12)可得其入渗速率为 (18) 式中iB-m为B基质域入渗速率。 联立式(9)与式(18),可得B基质域积水时间tp,B-m的隐式表达式: (19) 显然,B基质域与L基质域的积水时间相等。 B基质域表面积水后(裂隙域积水前),其边界条件由流量边界转为变水头边界。根据式(3),iB-m可表示为 (20) 式中:hc既为B基质域的表面水头高度,也为裂隙内的水位高度;IB-m为B基质域累积入渗量。 根据累积入渗量与入渗速率的导数关系,IB-m的隐式微分表达式为 (21) 将式(7)、式(20)表达式代入式(21),可得IB-m关于时间的常系数隐式微分方程: (22) 2.2.3 入渗方程(t≥tp,c) 当t≥tp,c时,首先确定裂隙域积水时间。定义有效裂隙深度Dc表示裂隙有限的容水空间,当裂隙内水位深度达到有效裂隙深度时,裂隙域即产生积水,由hc表达式可得: Ic-IB-m=Dc (23) 式(23)可通过式(22)得到的Ic、IB-m的时间变化曲线求解。 然后,裂隙域积水后,整个土体表面均开始产生积水,在土层缓倾斜的条件下,将产生径流,此时L基质域仍将处于弱积水状态,其入渗速率与累积入渗量仍可按式(12)、式(14)计算。 B基质域在裂隙域积水后将处于定水头边界条件直至降雨停止,其累积入渗量的隐式微分表达式为 (24) 因此,通过式(10)(11)(15)(17)(22)(24),可求得降雨期间各域任一时刻的累积入渗量。最后,各域的湿润锋深度按照容水孔隙空间大小可计算为 (25) zc=Dc-hc (26) (27) 式中:zL-m、zB-m、zc分别为L基质域、B基质域及裂隙域的湿润锋深度;Sm,a为L基质域面积率的平均值;Sc,a为裂隙域面积率的平均值;θs,m、θ0,m分别为基质域的饱和体积含水率与初始体积含水率。 总体说来,本文所提模型主要包括以下参数:a、b、w0、ws、tmid、tcon、r、Km、nm、Dc、sf,m、λ。除了最后2个参数,其他参数均可通过试验获得,具有较高的实用性。其中,sf,m可由Morel-Seytoux等[28]提出的预估模型求得。 选取文献[28]边坡足尺模型试验用土作为模拟对象,土体基本物理及水力学参数:相对密度为2.72,液限为35.7%,缩限为8.2%,塑性指数为17.3%,最佳含水率为17%,最大干密度为1.71g/cm3,自由膨胀率为42.5%。土体水力学拟合参数αm为0.002mm-1、mm为0.53,初始体积含水率为20.7%,饱和体积含水率为38.1%,残余体积含水率为10.1%,饱和渗透系数为8.45×10-3mm/min,nm为0.174,sf,m为173.36mm。土体裂隙率与质量含水率的线性关系式为(土体初始质量含水率为14.7%,饱和质量含水率为27.6%)为 β=-0.0019w+0.0542 (28) 不同降雨强度下的土体入渗试验测得表层土体(2~5cm)的质量含水率变化曲线及Boltzmann生长模型拟合曲线如图2所示。随后开展降雨强度、裂隙初始面积率、裂隙深度变化对雨水入渗过程的影响分析,各工况模拟参数见表1。 表1 不同工况模拟参数Table 1 Simulation parameters of different conditions 图2 不同降雨强度下质量含水率变化拟合曲线Fig.2 Fitting curves of mass water content under different rainfall intensity 由图3可知,裂隙域累积入渗量在降雨前期小于L基质域入渗量,随后超过L基质域并快速增加;随着降雨过程的进行,L基质域入渗速率降低,累积入渗量增幅逐渐变缓;B基质域累积入渗量较少,后期受裂隙闭合影响较大,累积入渗量增幅减小。总体看来,裂隙域最终累积入渗量显著大于基质域,且随降雨强度增大而增大,增幅达29.73mm;L基质域的最终累积入渗量也随降雨强度增大而增大,但其增幅较小,仅为0.28mm;然而,B基质域最终累积入渗量却随降雨强度增加而减小,降幅分别为0.09mm及0.16mm。此外,随降雨强度增大,基质域积水时间与裂隙域入渗量超过基质域入渗量的时间均明显缩短。 图3 累积入渗量Fig.3 Cumulative infiltration amount 由图4可知,L基质域入渗深度随降雨时间增加增幅逐渐变缓;B基质域入渗深度积水后先陡增,后缓增,最后以近线性方式增加;裂隙域积水水位高度(入渗深度)逐步上涨,并在降雨强度为30mm/h及45mm/h的条件下与L基质域湿润锋(入渗深度)相交。总体看来,B基质域最终入渗深度远大于L基质域,并随降雨强度增大而增大,增幅分别为69mm及124mm;L基质域最终入深深度随降雨强度增大增幅较小,仅为1.486mm及0.5113mm;裂隙域内最终积水水位高度随降雨强度而增大,分别为22.02mm、51.76mm及81.65mm,均小于100mm,故裂隙域未达到积水产生的时间。 图4 入渗深度Fig.4 Infiltration depth 式(28)表明在初始质量含水率为14.7%时,裂隙面积率为2.63%,在饱和质量含水率为27.6%时,其裂隙面积率为0.176%。保持饱和含水率对应的裂隙率不变,通过改变初始含水率下的裂隙面积率,可模拟土体胀缩能力对降雨入渗的影响。模拟的工况参数见表1,计算结果如图5所示。 图5 不同初始裂隙面积率条件下累积入渗量与入渗深度Fig.5 Cumulative infiltration amount and infiltration depth with different initial crack area ratios 由图5(a)可知,随着裂隙面积率增大,裂隙域与B基质域的累积入渗量增大,L基质域累积入渗量逐步减小,裂隙域入渗量超过基质域入渗量的时间也逐步缩短。然而,总体看来,不同裂隙面积率下的各域最终入渗量差值相差较小,其中B基质域的变化较裂隙域和L基质域明显。由图5(b)可知,随着裂隙面积率增大,L基质域入渗深度逐渐减小,裂隙域积水水位深度增加,但二者变化均较小。B基质域入渗深度变化较大,主要表现为随裂隙面积率增大而减小。 由图6(a)可知,干缩裂隙深度为50mm时,裂隙域在第76.23分钟积满水,由于裂隙域按面积占比计算的降雨强度(18.2×10-3mm/min)大于土体饱和渗透系数(也大于B基质域入渗速率),故裂隙域内累积入渗量、积水水位高度将不再变化,此时B基质域表面由变水头边界转换为定水头边界,其最终累积入渗量较裂隙域未积水有所减小;当干缩裂隙深度为100mm及300mm时,裂隙域未积满水,二者各域累积入渗量变化曲线一致。由图6(b)可知,随着干缩裂隙深度增加,裂隙域内的积水水位与L基质域湿润锋深度相交的时间延后甚至不相交;B基质域最终入渗深度增加;L基质域入渗深度随裂隙深度增加无明显变化。 3.4.1 干缩裂隙对优势流入渗的影响 降雨强度增大不仅增加总降雨量,还会显著缩短裂隙两侧基质域表面积水时间,导致积水更早进入裂隙域,故裂隙域内最终累积入渗量随降雨强度增大而增大。同时,基质域入渗速率在表面积水后将不再受降雨强度控制,不同降雨强度下其最终入渗量差值主要由积水前雨水完全入渗引起,由于基质域积水时间较短,故不同降雨强度下的最终累积入渗量差值亦较小。值得注意的是,随降雨强度增大,裂隙面积减小速度加快,裂隙底部基质域在积水前按面积占比所获得的雨水完全入渗量减少,故其累积入渗量随降雨强度增大不增反减。此外,由于降雨时裂隙两侧基质域膨胀引起的面积增量远小于基质域面积,且不同降雨强度下基质域累积入渗量相差较小,故其入渗深度变化曲线较为平滑且变化较小;裂隙域内积水水位深度与其累积入渗量成正比,故其随降雨强度增加而增加;虽然裂隙底部基质域累积入渗量因裂隙面积的快速减小而减小,但裂隙面积减小不仅使其上部水头快速增大,还使雨水下渗所要填充的总容水孔隙空间减小,故其下渗深度仍随降雨强度增大而增加。 裂隙面积率通过影响各域的受水面积及容水孔隙空间进而影响入渗量及入渗深度。当其他参数不变时,较小的裂隙初始面积率会使优势流入渗量(裂隙域与B基质域入渗量)减小,但却会引起优势流入渗深度的增加。例如,当降雨强度为15mm/h,裂隙深度为100mm时,1.43%初始裂隙面积率的优势流最终入渗深度大于裂隙初始面积率为2.43%与5.43%的入渗深度。上述模拟结果或可解释在诸多前人的试验中存在的普遍现象[7,29],即在裂隙或者大孔隙不易被观察到的土体中,优势流仍使雨水快速下渗至土体深部。 裂隙深度主要影响裂隙域积水时间、优势流入渗量及入渗深度。随裂隙深度增大,其容水空间也逐渐变大,当不限制降雨时长时,裂隙域积水时间会逐渐变长。裂隙域积水后,大量雨水通过径流流失,使得优势流入渗量减小,其入渗深度随之减小。本文的模拟结果表明,土体干缩裂隙产生的优势流入渗量占总降水量的73.4%~91.4%,优势流入渗深度为裂隙深度的3.1~7.2倍。 3.4.2 优势流模型存在的问题 由于本文的优势流模型是基于Green-Ampt入渗理论发展而来的,故该模型也将水分在土体基质域的运移过程视为活塞流,且湿润锋后的土体假设达到完全饱和,这有可能高估基质域内(L基质域和B基质域)的累积入渗量,进而高估了优势流的入渗深度。此外,雨水进入干缩裂隙时,部分雨水会通过裂隙侧壁水平入渗至基质域,但该模型目前的形式中未考虑裂隙侧壁的水平入渗,其入渗量可能成为了模型中裂隙域内积水深度hc及B基质域入渗量IB-m的一部分,导致相应计算结果偏大。有学者认为干缩裂隙形成后其侧壁会产生显著的毛细屏障作用[28],水平入渗效应被严重削弱,即该部分入渗量对计算结果的影响可能较小,但仍需进一步验证。 尽管本文所提优势流模型存在上述问题,但其具有较为明确的物理意义且较好地体现了干缩裂隙对雨水入渗过程的影响。同时,所提优势流入渗模型将干缩裂隙作为容水空间而非透水性材料,与实际物理过程相符,还可避免为裂隙赋水力学参数带来的不便与误差。该模型还可为目前大量应用Green-Amp入渗理论预测边坡失稳的模型提供新思路。未来对该模型的改进应将裂隙底部的雨水弥散与侧壁水平入渗考虑在内。 a.土体干缩裂隙产生的优势流入渗量占总降水量的73.4%~91.4%,优势流入渗深度为裂隙深度的3.1~7.2倍。 b.降雨强度增大使基质域积水时间缩短,裂隙闭合速度加快,裂隙两侧基质域及裂隙域内累积入渗量增加,裂隙底部基质域累积入渗量减小,各域入渗深度均增大。 c.干缩裂隙动态变化显著影响优势流入渗量与入渗深度。降雨过程中裂隙率减小使优势流入渗量减小;裂隙初始面积率增大使基质域入渗量及入渗深度减小,优势流入渗量增大但入渗深度减小;裂隙深度增大主要使优势流入渗深度增大。 d.模型计算结果可较好地反映干缩裂隙雨水入渗的规律,与前人试验结果相符。同时,模型将双孔隙域入渗理论中的裂隙域作为容水空间而非渗透性材料,与实际干缩裂隙入渗过程相符,参数选取简单快捷。2 模型控制方程
2.1 双孔隙域Green-Ampt入渗模型
2.2 分阶段基质域与裂隙域入渗方程
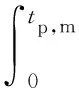
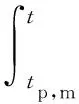
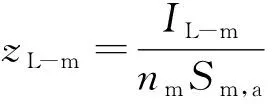
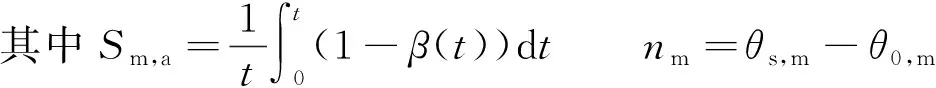
3 实例模拟验证


3.1 不同降雨强度的影响

3.2 不同初始裂隙面积率的影响
3.3 不同裂隙深度的影响
3.4 讨论
4 结 论
