考虑孔隙比影响的堆石料湿化试验及湿化模型

2024-01-23王柳江毛航宇刘斯宏傅中志韩华强沈超敏

河海大学学报（自然科学版） 2024年1期

王柳江,毛航宇,2,刘斯宏,傅中志,韩华强,沈超敏

(1.河海大学水利水电学院,江苏南京 210098; 2.河海大学土木与交通学院,江苏南京 210098;3.南京水利科学研究院岩土工程研究所,江苏南京 210029)

土石坝具有可就地取材、对复杂地形地质条件适应性好等优点,是我国水电开发的主力坝型[1]。受大坝蓄水、降雨入渗、库水位升降的影响,筑坝堆石料会由干态转变为湿态,在此过程中产生湿化变形[2-4],从而产生较大的湿陷变形[5]和不均匀沉降[6-7],损坏坝体防渗系统。因此开展堆石料湿化变形研究对保证土石坝工程的安全运行具有重要意义。

堆石料的湿化试验主要有单线法和双线法2种[8-9]。单线法更接近堆石坝实际浸水饱和过程,因此,现有湿化试验大多采用单线法[10-12],即在维持三轴剪切应力条件下对试样进行蓄水饱和并测量湿化变形[13]。朱俊高等[14-19]通过试验分析了湿化应力大小、颗粒级配、母岩岩性、应力路径、降雨强度、干湿循环等因素对堆石料湿化变形的影响,探究了堆石料湿化变形的一般规律。除上述影响因素外,密实度同样会影响堆石料的湿化变形,左元明等[20-21]通过分析不同密度的堆石料湿化试验结果发现,等应力状态条件下,密度的提高会减小堆石料的湿化变形量。张延亿[22]的试验结果则表明,制样密度较低时湿化变形随着密度的增大而减小,当制样密度超过一定值后湿化变形随着密度的增大略微增大。魏松[23]开展了密实堆石料的湿化试验,观察到了低围压条件下湿化轴向应变大于高围压的现象,以及低围压高应力水平条件下体积膨胀的现象。密实度对粗粒料湿化变形规律的影响较为复杂,有必要开展更为系统的研究。

湿化模型一般是通过构建拟合公式对湿化试验规律进行描述。例如:李广信[24]分别采用双曲线函数及幂函数描述湿化轴向应变及湿化体积应变规律;程展林等[25]分别采用指数函数及线性方程描述湿化轴向应变及湿化体积应变规律。上述模型均是通过不同的拟合方程直接计算湿化轴向应变与湿化体积应变。考虑到三轴湿化试验中的湿化体积应变测量结果可能存在误差,迟世春等[26]通过分析大量湿化试验结果发现,湿化过程中体积应变增量与轴向应变增量的比值保持不变,由此提出通过轴向应变计算结果间接得到体积应变的建模思路,并基于非线性弹性理论提出了湿化割线模量及泊松比模型。周雄雄等[27]基于试验结果推导了湿化体积应变与湿化轴向应变比值的计算公式,结合湿化轴向应变与应力水平的双曲线关系,间接计算湿化体积应变。湿化试验是一种应力状态恒定的特殊试验,参考弹塑性本构理论[28-29],可认为湿化过程中湿化体积应变增量与湿化轴向应变增量的比值为湿化剪胀比,其计算公式即湿化剪胀方程,结合合适的湿化轴向应变计算公式,即可间接得到湿化体积应变。由于湿化剪胀比的数值可正可负,因此间接计算湿化体积应变的方法在综合反映湿缩及湿胀等复杂湿化体积应变规律时具有一定的优势。

本文对某堆石坝的坝壳料进行了一系列不同初始孔隙比的单线法大型三轴湿化变形试验,分析了初始孔隙比及应力状态对湿化变形的影响规律, 并基于试验结果建立了一个能够考虑初始孔隙比影响的变形计算模型。

1 试验内容及方法

1.1 试验内容

湿化试验在河海大学的大型三轴仪上进行,试样直径300mm,高度600mm。试验所用堆石料为某混合坝右岸心墙堆石坝的坝壳料,母岩岩性为粉质砂岩,母岩抗压强度为94.16 MPa,软化系数为0.61。由于设计级配最大粒径较大,对设计级配进行了缩尺,缩尺方法采用相似级配法和等量替换法相结合的混合法,图1为设计级配曲线及试验级配曲线。为研究初始密实度对湿化变形特性的影响,制样时控制初始孔隙率为19%、22%和25%,对应的初始孔隙比为0.234、0.282、0.333。

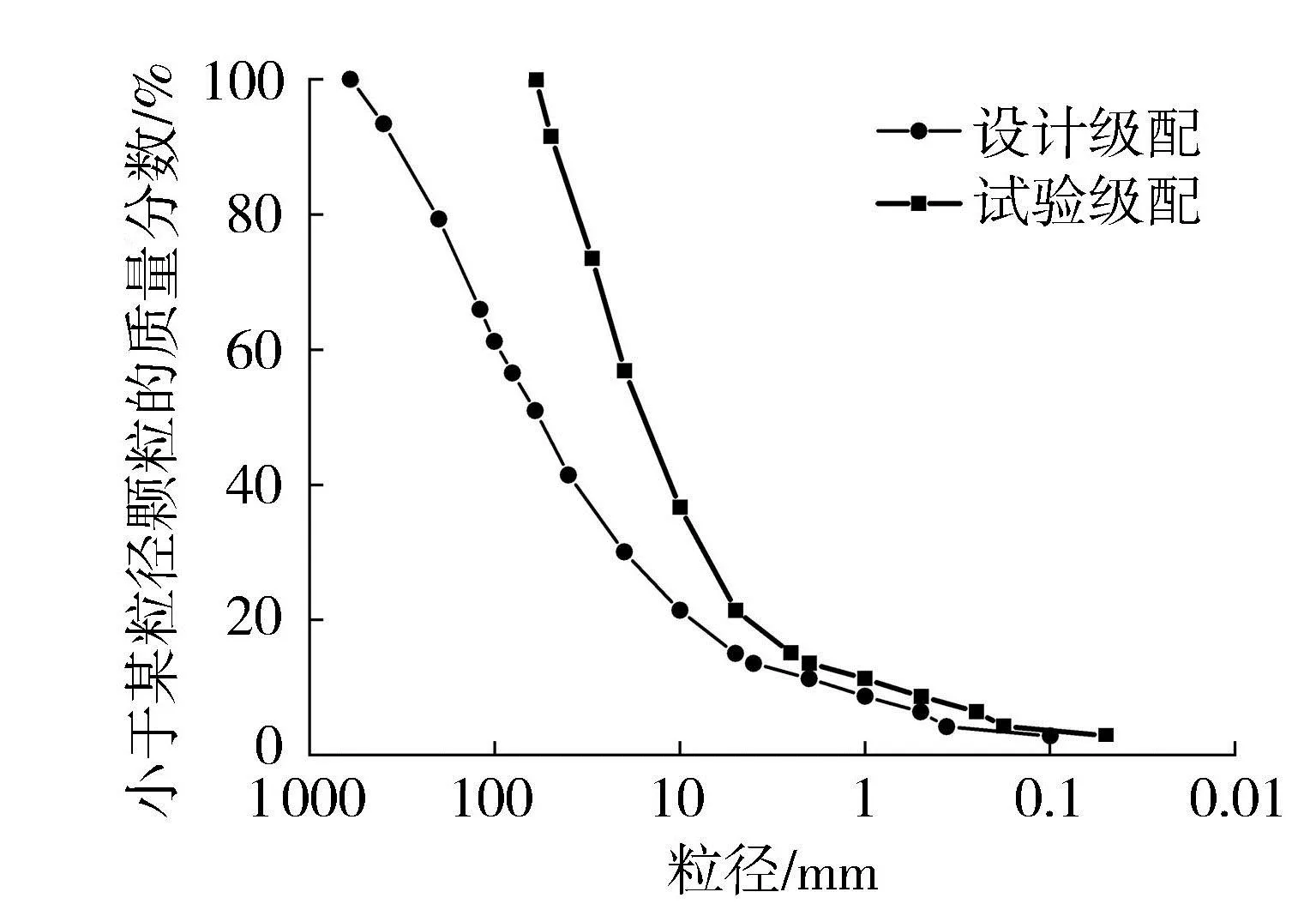
图1 试验材料级配曲线Fig.1 Grain size distribution curve of test material

1.2 试验方法

参考GB/T 50123—2019《土工试验规程》开展单线法湿化试验,试验步骤:①干样三轴剪切(图2中的OA段)。试样初始状态为干态,该阶段按干态试样常规三轴压缩试验方法进行,采用应变控制式加载, 加载速率为0.02%/min。试验过程中采集试样的轴向变形、外体积变化以及轴向力,加载直至试验预设应力水平SL所对应的偏应力(σ1-σ3)w。②干样变形稳定(图2中的AB段)。剪切至预定轴向压力后,保持围压及轴向应力不变,稳定3～5h后观察试样轴向应变变化量,当30min内轴向应变变化量小于0.01%,判定干样变形稳定。③浸水湿化(图2中的BC段)。干样变形稳定后继续保持围压和轴向应力不变,同时从试样通水,进行水头饱和,待通入试样的水从试样顶部连续流出且无气泡排出时认定饱和完成,随后静置至试样变形稳定。浸水湿化过程中记录试样的轴向变形及体积变化,其中体积变化仍采用外体积变化量测方法测量。当30min内轴向应变的变化量小于0.01%时可认为湿化变形稳定,随后根据记录的变形量计算湿化轴向应变Δεa,w及湿化体积应变Δεv,w。④湿样三轴剪切(图2中的CD段)。切换加载控制方式,采用应变控制式加载进一步剪切试样到破坏,加载速率为0.02%/min。

图2 典型湿化试验曲线Fig.2 Typical wetting deformation test curve

分别对不同初始孔隙比(e0=0.234,0.282,0.333)的试样,在不同围压(σ3=0.2,0.4,0.8,1.2MPa)条件下开展三轴湿化试验,每个围压条件下分别设置4个不同的湿化应力水平,共计48个试样。

2 试验结果与分析

2.1 应力-应变关系曲线

图3中应力-应变关系的水平段即为湿化变形段,其对应的轴向应变及体积应变差值分别为湿化轴向应变及湿化体积应变。由图3可知,不同初始孔隙比试样的湿化规律基本一致,即湿化轴向应变和湿化体应变均随着湿化应力水平的增大而增长。此外,当初始孔隙比较小时,即试样密实程度较高时,其三轴剪切阶段的应力-应变曲线为应变软化型,体积变形表现为剪胀;随着初始孔隙比的增大,试样密实程度降低,其三轴剪切阶段的应力-应变曲线逐渐转变为应变硬化型,且剪胀性明显减弱。由于本文的试验工况较多,其余3个围压(σ3=0.4,0.8,1.2MPa)条件下的试验曲线不再给出,仅在表1中列出所有试验工况对应的湿化变形统计结果。

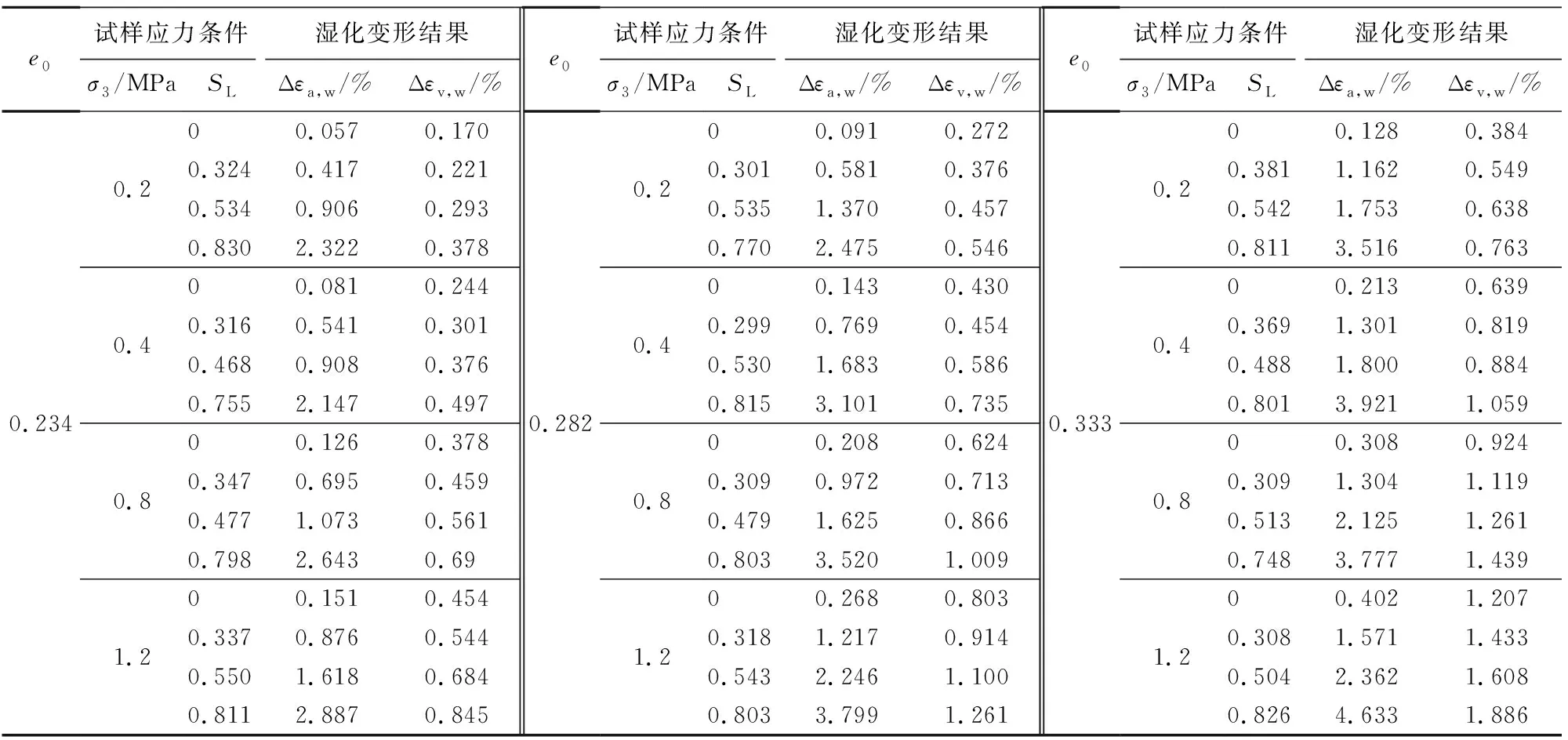
表1 不同试验工况的湿化变形统计结果Table 1 Statistical results of wetting deformation under different test conditions

图3 三轴湿化试验应力-应变关系(σ3=0.2MPa)Fig.3 Stress-strain relationship of wetting tests (σ3=0.2MPa)

2.2 湿化变形规律分析

由图4可知,堆石料的湿化轴向应变不仅与湿化应力水平SL相关,还与σ3相关,随着SL和σ3的增大,对应的湿化轴向应变也呈增大趋势,且当SL达到0.5后,湿化轴向应变随着SL的增加而急剧增加;堆石料湿化体积应变同样随着SL和σ3的增大而增大,且与SL之间呈较好的线性关系。

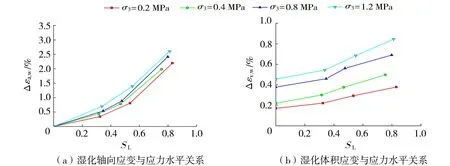
图4 堆石料湿化应变与应力水平关系(e0=0.234)Fig.4 Relationship between wetting strain and stress level of rockfill (e0=0.234)

由图5可知,在相同σ3下,湿化体积应变随着初始孔隙比的减小而减小,当σ3较小时,初始孔隙比对湿化体积应变的影响较小,但随着σ3的增大,初始孔隙比对湿化体积应变的影响明显增大,即提高堆石料的密实度可以有效减小湿化产生的体积变形。

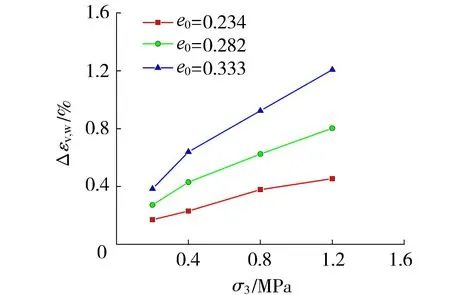
图5 各向等压条件下(SL=0)湿化体积应变与围压的关系Fig.5 Relationship between wetting volumetric strain and confining pressure under isotropic pressure (SL=0)

由图6可知,当SL相同时,随着初始孔隙比的减小,堆石料的湿化轴向应变和体积应变均有明显降低;对于湿化体积应变,在不同SL下,由密实度变化引起的堆石料湿化体积变形差异基本相等;而对于湿化轴向应变,当SL较低时,堆石料密实度增加对减小湿化轴向应变的效果不明显,但在SL较高时,堆石料密实度增加可有效减小湿化轴向应变。堆石料的湿化变形主要源于颗粒破碎后的颗粒重排,且变形均表现为体缩变形。对于密实度较高的试样,堆石颗粒湿化破碎后体积进一步缩小的空间较小,相应的湿化变形较小。因此,在实际工程中可以通过提高压实质量减小湿化变形量。

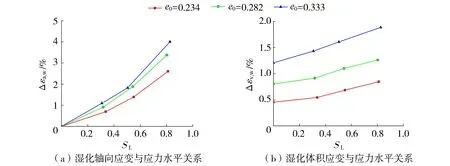
图6 不同初始孔隙比条件下堆石料湿化应变与应力水平关系(σ3=1.2MPa)Fig.6 Relationship between wetting strain and stress level under different initial void ratio (σ3=1.2MPa)

3 湿化模型及验证

3.1 湿化剪胀方程

湿化变形过程中,体积应变与轴向应变的关系一般可近似认为是直线关系[25],即图2中体积应变-轴向应变关系的BC段。可以通过定义湿化剪胀比dw表示湿化过程中体积应变与轴向应变直线关系的斜率:

dw=Δεv,w/Δεa,w

(1)

周雄雄等[27]通过分析大量堆石料单线法湿化试验结果发现,当dw相等时,相应的平均正应力p和广义剪应力q关系为经过原点的直线,即dw与应力比η存在一一对应关系;进一步分析发现η与dw的试验点存在凹曲线、直线和凸曲线3种可能,而指数函数可以同时描述这3种情况,基于材料各向同性假设,给出了如下表达式:

η=q/p=a(bdw-b3)

(2)

式中a和b为拟合参数。

根据本文试验结果统计不同初始孔隙比条件下堆石料的dw与η的关系,如图7所示。由图7可知,不同初始孔隙比条件下,η与dw的试验点基本都分布在同一条曲线上,即η与dw的关系基本不受初始孔隙比的影响。利用式(2)对试验点进行拟合,发现拟合效果较好,相应的拟合参数a=2.38,b=0.26。

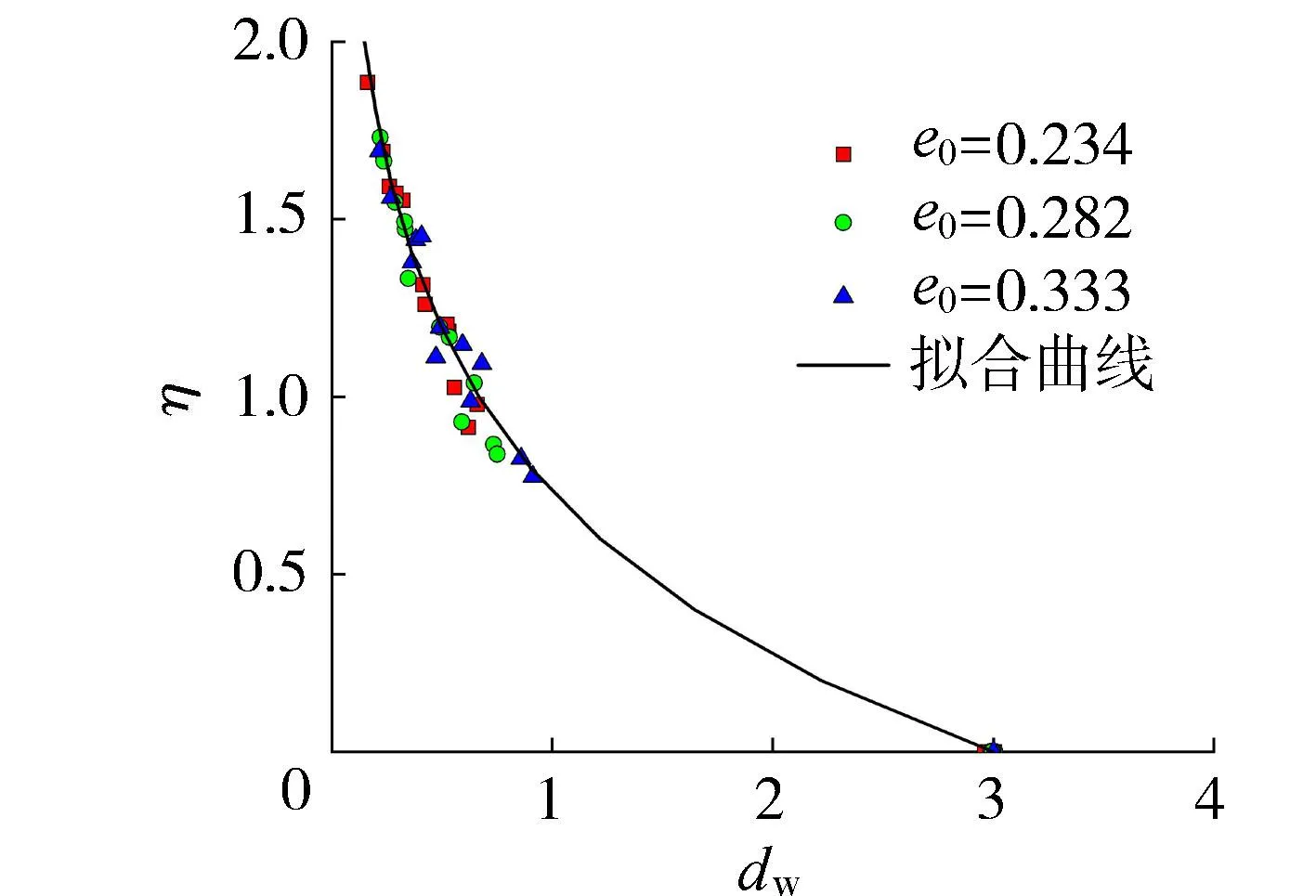
图7 堆石料湿化剪胀比与应力比的关系Fig.7 Relationship between dilatancy ratio and stress ratio

对式(2)进行变换,可得到湿化剪胀方程为

dw=logb(η/a+b3)

(3)

利用式(3)可计算不同湿化应力比条件下的湿化剪胀比,得到湿化体积应变与湿化轴向应变的比例关系。

3.2 湿化轴向应变

通过对本文湿化试验数据的分析,发现湿化轴向应变与湿化时的应力水平以及围压均存在一定的相关性。程展林等[25]提出了基于指数函数的湿化轴向应变模型,但该模型仅考虑了与湿化应力比之间的相关性,未考虑围压的影响。为此,本文以湿化过程中的应力比与平均正应力作为变量,提出湿化轴向应变表达式:

Δεa,w=Alg(p/pa)eBη

(4)

式中:A和B为模型参数;pa为大气压。

由于η和p分别对应SL和σ3,说明式(4)能够同时考虑SL和σ3的影响。由图8可知,对于初始孔隙比相同的试样,其在不同σ3下的Δεa,w/lg(p/pa)与η试验点基本在一条曲线上,说明式(4)能够统一考虑围压对湿化轴向应变的影响。此外,对于初始孔隙比不同的试样,Δεa,w/lg(p/pa)与η的关系为3条趋于平行的曲线,其中,在相同η下,初始孔隙比越大,对应的Δεa,w/lg(p/pa)越大。采用式(4)对图8中的试验数据进行拟合,拟合结果见表2。由表2可知,式(4)拟合效果很好,相关系数均大于0.97,其中,参数B基本保持不变,而参数A随初始孔隙比的增大呈指数函数增长趋势。基于此,对式(4)进行修正:

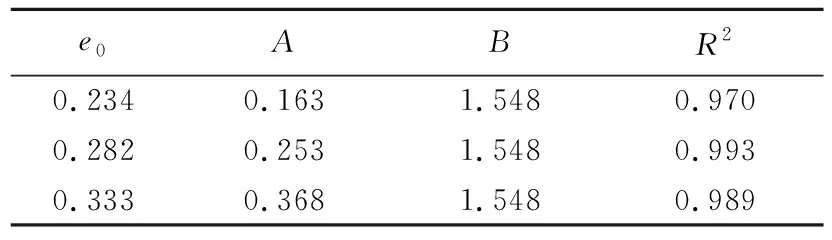
表2 式(4)参数拟合结果Table 2 Fitting results of parameters for Equation (4)

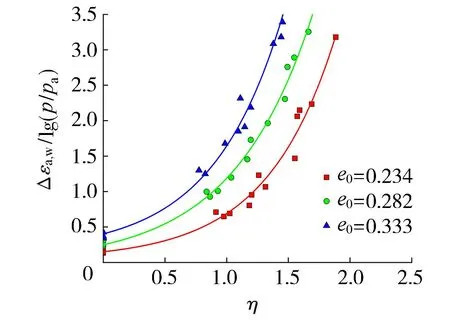
图8 Δεa,w/lg(p/pa)与η的关系Fig.8 Relationship between Δεa,w/lg(p/pa) and η

(5)

式中A0和n为模型拟合参数。

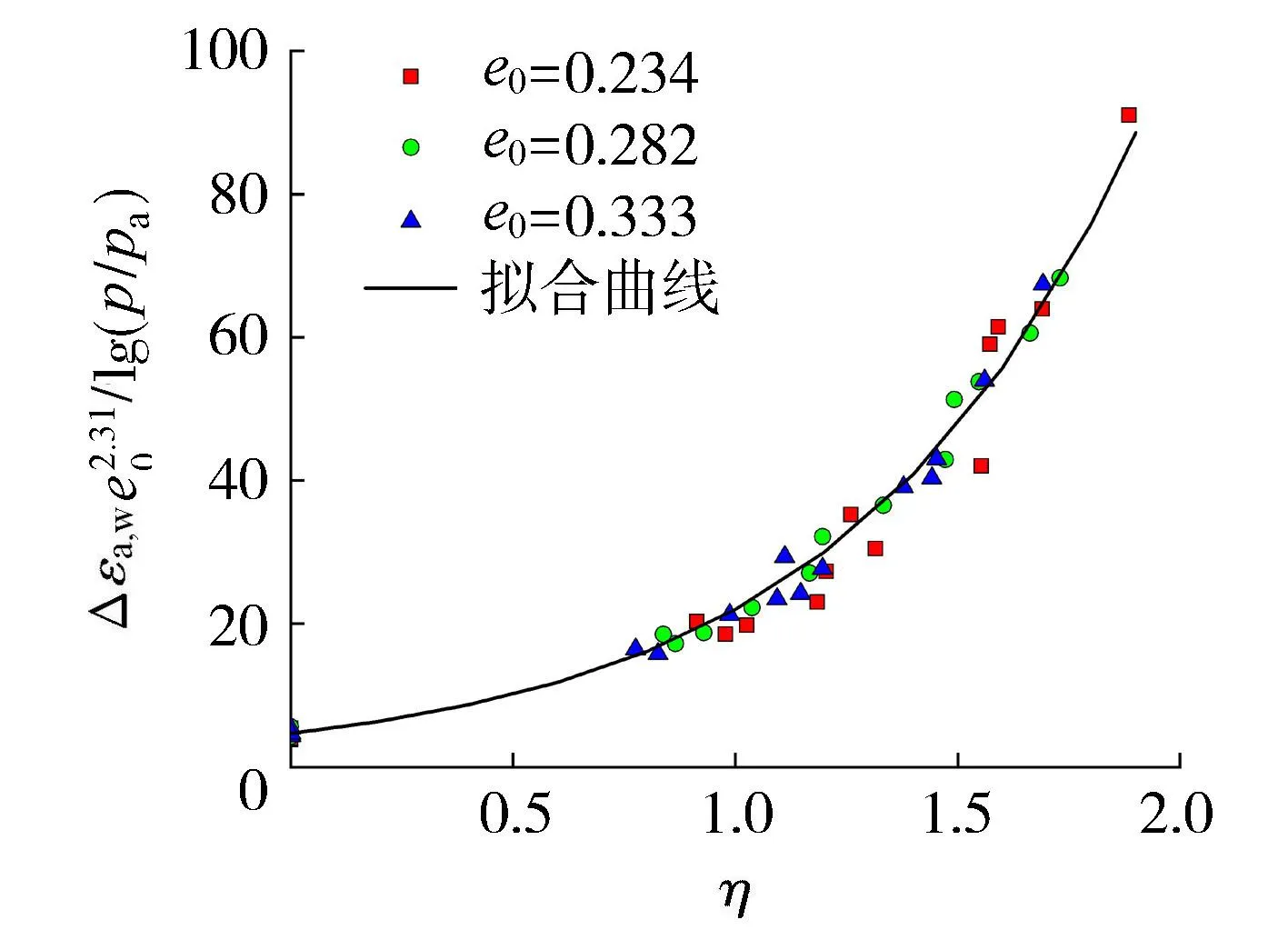
图9 与η的关系Fig.9 Relationship between

联立式(3)和式(5),即可得到湿化体积应变表达式:

(6)

由式(6)可知,本文提出的湿化模型参数简单,仅包含5个参数,分别为a、b、A0、n、B,通过三轴湿化试验即可获得。考虑到在有限元分析计算中常用广义剪应变作为一般应变分量,而在轴对称三轴应力状态下广义剪应变εs与轴应变以及体应变有如下对应关系:

εs=εa-εv/3

(7)

在开展有限元分析计算时,可以联立式(5)(6)(7),将轴向应变转换为广义偏应变。

3.3 模型验证

根据本文试验结果,拟合得到模型参数:a=2.38,b=0.26,A0=4.676,n=2.31,B=1.548。将拟合参数代入湿化模型,即可得到不同初始孔隙比试样在不同围压和应力水平下的湿化轴向应变和湿化体积应变。由图10～12可知,对于不同初始孔隙率的堆石料,其在不同围压和湿化应力水平下的模拟结果与试验数据吻合很好。

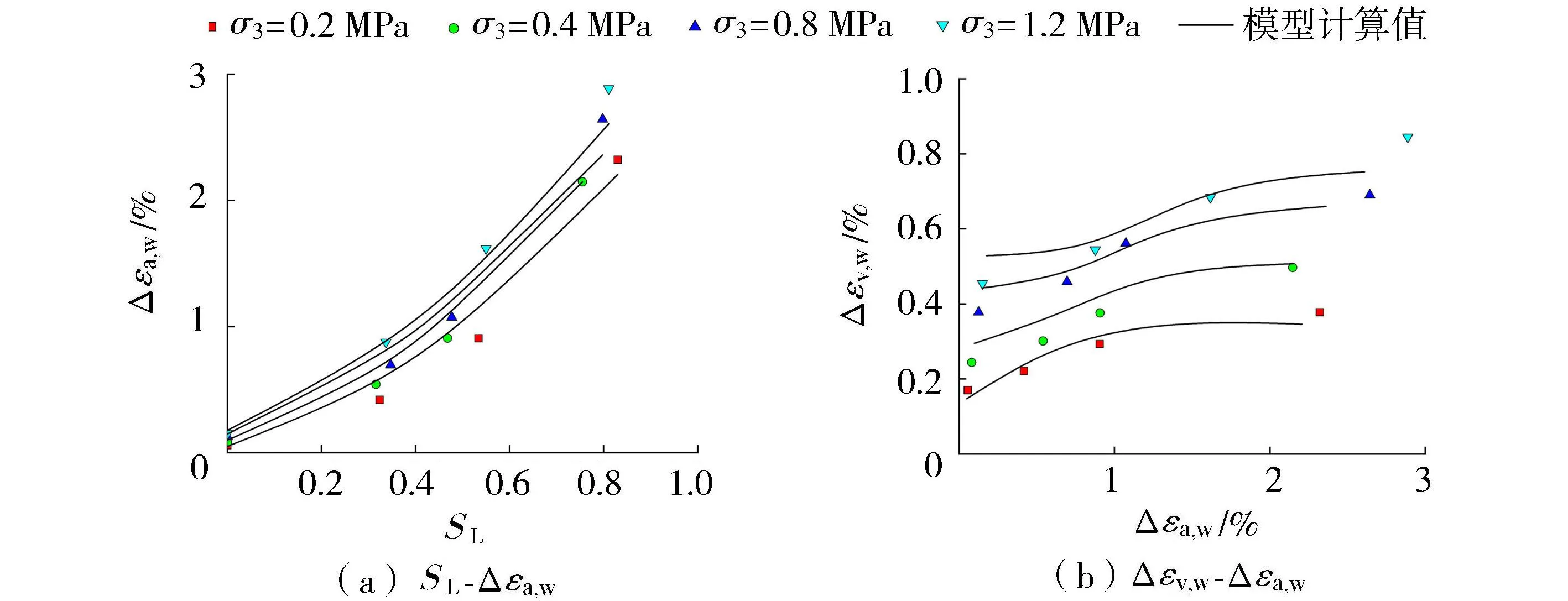
图10 堆石料湿化试验模拟(e0=0.234)Fig.10 Simulation of rockfill wetting test (e0=0.234)

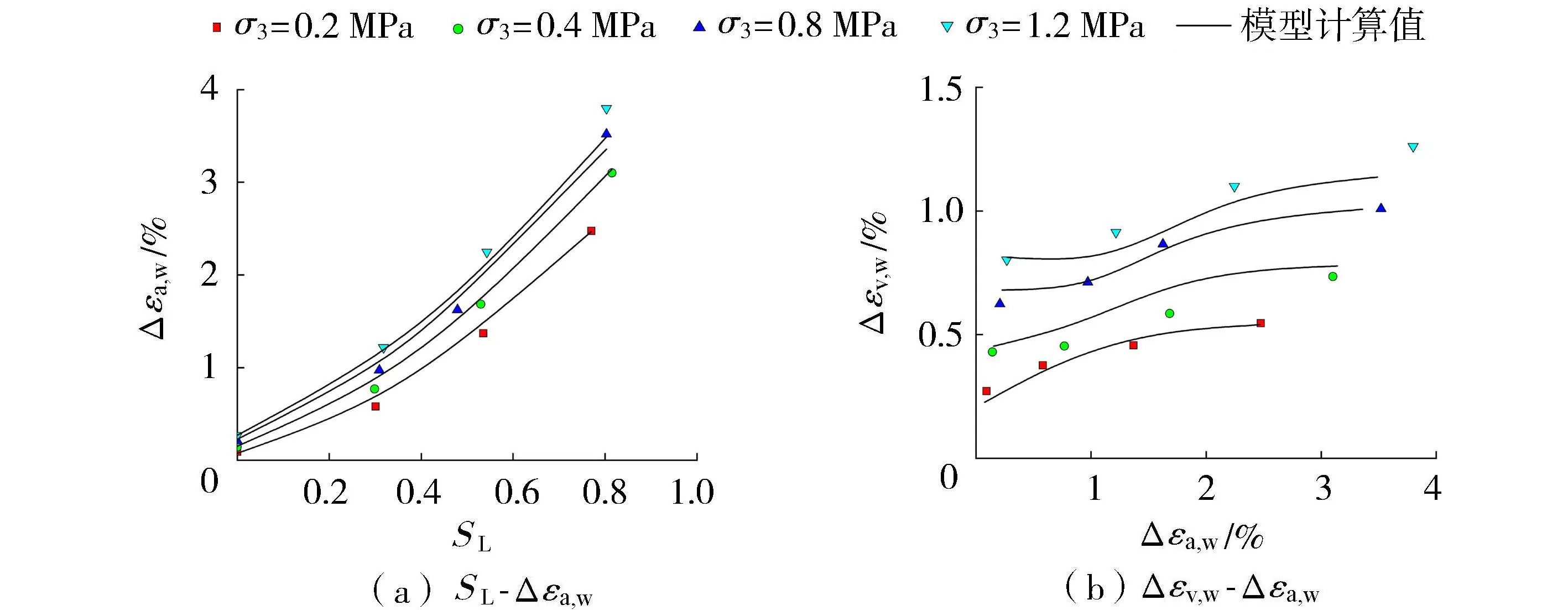
图11 堆石料湿化试验模拟(e0=0.282)Fig.11 Simulation of rockfill wetting test (e0=0.282)

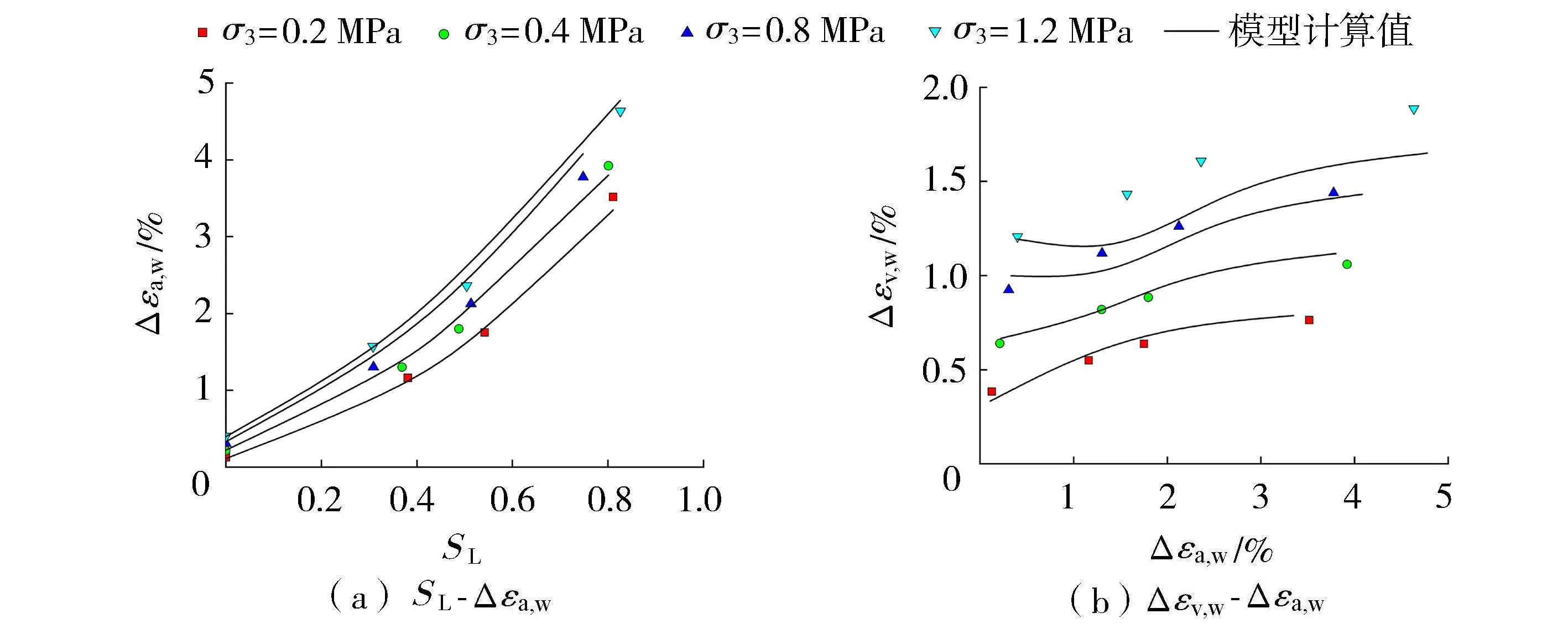
图12 堆石料湿化试验模拟(e0=0.333)Fig.12 Simulation of rockfill wetting test (e0=0.333)

工程中通常采用李国英等[30]改进后的沈珠江模型(又称沈珠江三参数湿化模型)计算湿化应变:

Δεv,w=Cw(σ3/pa)nw

(8)

Δγw=DwSL/(1-SL)

(9)

式中:Δγw为湿化剪切应变;Cw、Dw、nw为参数。

由式(8)可知,相同围压下,湿化体积应变保持不变,即湿化体积应变不随湿化轴向应变的变化而变化,而本文试验结果显示,湿化体积应变与初始密实状态、围压以及湿化应力水平均相关,随着湿化轴向应变的增加,湿化体积应变同样呈增长趋势。对于式(9),尽管其能够考虑湿化应力水平对湿化剪切应变的影响,但目前尚无法考虑堆石料压实状态的影响。因此,沈珠江三参数湿化模型在描述堆石料的湿化体积应变时有一定局限性。相比较而言,本文提出的模型能够较好地反映不同密实状态下的堆石料湿化变形特性,能够更好地预测实际工程中堆石料的湿化变形。