代理模型参数率定方法在TOPKAPI模型中的应用

汤 岭,王海军,李致家,黄迎春,盛奕华

(1.河海大学水文水资源学院,江苏 南京 210098; 2.山东省水文中心,山东 济南 250013)

随着计算机技术的发展,水文模型发展迅速,从单一模型不断优化改进为综合模型[1-3],再到如今广泛使用的基于物理基础的分布式水文模型[4-7]。分布式水文模型大多以DEM网格为计算单位,参数均具有明确的物理意义,每个网格代表的实际下垫面情况均可以通过参数反映[8],水流运动一般通过连续方程和动力方程求解,能较全面地描述水文过程。但由于其计算量大、参数数量多[9-10],模型需要较长时间的模拟,且相比单目标优化[11-13],多目标优化更是需要长时间运行模型才能找到全局最优解。因此,分布式水文模型参数优化的时效问题成为了热点和难点问题[14-16],制约了模型的实用性。

基于代理建模的优化方法是一种减少参数优化计算量的有效方法,已广泛应用于水文建模和水资源管理中[17]。近年来,出现了许多基于代理建模的多目标优化方法,其中一些是基于经典的多目标非支配排序,使用廉价代理模型替代昂贵的动态模型。例如:Syberfeldt等[18]提出了多目标并行代理辅助进化算法(multi-objective parallel substitute-assisted evolution algorithm, MOPSA-EA),该算法使用一个ANN作为代理,考虑了代理计算的不确定性和并行性;宋晓猛等[19]使用响应曲面对新安江模型进行参数优化,认为代理模型可有效降低计算效率且稳定性较好;Kourakos等[20]开发了一种基于模块化神经网络代理的多目标优化算法MOSA (multi-objective surrogate assisted algorithm ),在希腊圣托里尼的含水层管理中应用效果很好。

为解决复杂水文模型参数优化的时效问题,本文以沂河下游临沂水文站以上流域(临沂流域)为研究区进行洪水模拟,将多目标自适应代理模型优化(multi-objective adaptive surrogate modeling-based optimization,MO-ASMO)算法应用在TOPKAPI(topographic kinematic approximation and integration)模型的参数率定中,并与传统多目标优化算法NSGA-Ⅱ(non-dominated sorting genetic algorithm Ⅱ)、NSGA-Ⅲ进行比较,以期提高TOPKAPI模型在湿润半湿润地区的模拟精度。

1 研究方法

1.1 TOPKAPI模型

TOPKAPI模型由Todini[21]基于运动学和流域地形学结合的理念构建,该模型将研究区域细分为多个网格,并假设当前计算网格只与下游唯一的网格相连接,通过网格之间的高程差计算径流路线。空间上采用非线性运动波方程模拟水流运动,以3个结构上相似的非线性水库方程分别描述土壤、地表和河道中的水流运动规律,从而得到整个流域的水文过程。

1.2 NSGA-Ⅱ、NSGA-Ⅲ

NSGA-Ⅱ是Deb等[22]于2002年提出的多目标优化算法,由NSGA改进而来,降低了计算复杂度,并能保持种群的多样性;引入了精英策略,扩大了采样空间,防止最佳个体的丢失。具体流程如图1所示。

NSGA-Ⅱ在求解目标维数较低的问题时较为有效,但面对三维及以上的高维目标优化问题效果不理想[23]。NSGA-Ⅲ的整体流程与NSGA-Ⅱ一致,皆通过交叉变异和非支配排序得到Pareto前沿,两者的区别在保持种群多样性方面,NSGA-Ⅱ是利用拥挤度比较操作,NSGA-Ⅲ则通过参考点机制。NSGA-Ⅲ具体流程如图2所示。

1.3 MO-ASMO算法

MO-ASMO算法可以满足复杂的基于物理基础的分布式水文模型的参数优化[24],主要有3个步骤:

a.选择最合适的初始采样和代理建模算法。用好格子点法[25]作为初始采样方法,高斯回归(GPR)[26]作为代理建模算法。GPR是一种具有多种协方差函数的灵活回归方法,可以适应不同的插值和回归任务。此外,超参数值还可以控制GPR的行为。例如,如果噪声项设置为0,则GPR可视为多维插值方法。如果特征长度较大,则GPR是平滑的,如果较小,则GPR对输出的微小变化很敏感。为了选择合适的超参数值,使用SCE-UA算法最大化边缘似然函数。

b.使用最具代表性的Pareto子集进行模拟。这种自适应抽样策略可以简单而有效地平衡收敛性和多样性。

c.通过设置MO-ASMO算法参数调整模型运行终止条件,本文设置算法参数为运行迭代次数。

MO-ASMO算法具体流程如下:①采用GLP抽样生成初始待率定参数矩阵,放入TOPKAPI模型生成模拟流量过程线并计算目标函数矩阵。②将参数矩阵和目标函数矩阵输入GPR代理模型,得到相关关系。③原MO-ASMO算法用NSGA-Ⅱ对代理模型进行多目标优化,本文考虑到有3个目标函数,将其改进使用NSGA-Ⅲ对代理模型优化得到Pareto解集,取20%的Pareto最优解放入TOPKAPI模型运行并生成目标函数矩阵。④利用新生成参数矩阵和目标函数矩阵更新训练数据,再次构建代理模型,在满足回归迭代次数条件前,重复步骤②～④。⑤输出最终Pareto前沿对应的参数样本和目标函数值。

1.4 Morris法

Morris法是Morris[27]于1991年提出的一种全局敏感性分析法, 通过独立随机的“一次变化法”抽样,再评价每个参数值的改变对目标函数的影响,从而可以定性分析出敏感参数。

2 实例应用

2.1 研究区概况

临沂流域面积为10316km2,呈扇形,属温带大陆性季风气候。该流域雨量分布时空不均,夏秋多,冬春少,年降水量约800mm;最高气温36.5℃,最低气温-11℃,全年平均气温14.1℃,沂河上兴建了大量的水利拦河工程,有跋山水库、唐村水库、岸堤水库、许家崖水库4个大型水库,4个水库控制区域产生的径流作为入流处理。

2.2 基础数据及预处理

TOPKAPI模型需要输入的数据包括DEM、土壤类型、气象数据等。本文DEM (图3)来自地理空间数据云SRTM数据,分辨率为1 km;土壤类型数据(图4(a))来自世界土壤数据库,分辨率为1 km;土地利用数据(图4(b))来自中国科学院资源环境科学数据中心,采用中国土地利用现状遥感监测数据库数据集,分辨率为1 km;通过Strahler方法(图4(c))对河道分级;气温数据来源于中国气象数据网(http://data.cma.cn),采用中国地面气候资料日值数据集(V3.0);降水量、实测流量和实测入流等数据由淮河水文局提供,时间跨度为2011—2021年,时段间隔为2h。

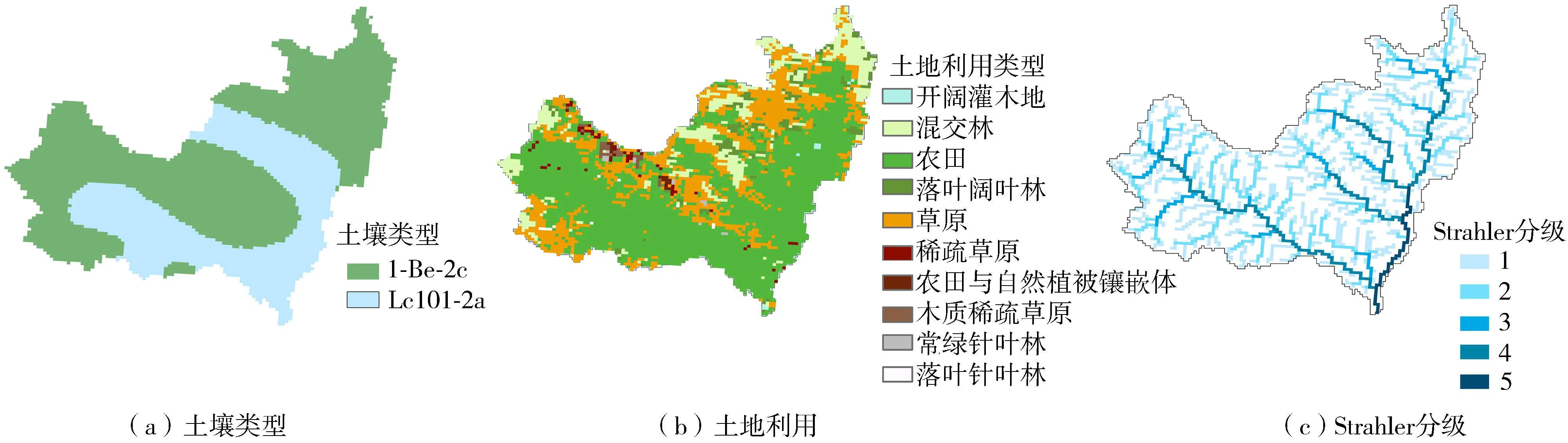
图4 临沂流域土壤类型、土地利用分布和Strahler分级Fig.4 Soil type, land use distribution and Strahler grading chart in the Linyi Basin

2.3 评价指标

在半湿润半干旱的淮河流域,洪水过程常常历时短、涨水退水过程迅速,因此选择洪峰流量、峰现时间和纳什效率系数为主要评价指标。

洪峰流量误差REp表示单场洪水过程实测洪峰与模拟洪峰的相对误差绝对值,越小表明预报洪峰流量偏离实测洪峰流量的幅度越小。峰现时间误差TEp表示单场洪水过程模拟的峰现时间与实测峰现时间的绝对误差;纳什效率系数NSE表示单场洪水过程模拟系列与实测系列之间拟合程度,越接近1,表明模拟系列与实测系列整体拟合越好。设MREp、MTEp、MNSE分别为多场洪水的平均洪峰流量误差、峰现时间误差和纳什效率系数。

2.4 Morris法分析结果

TOPKAPI模型参数众多[28],优化不敏感参数会降低率定效率。因此本文采用Morris法对23个TOPKAPI模型参数抽样100次,对得到的2300组样本进行敏感性分析,选取率定期10场洪水的各参数敏感性平均值作为该参数的整体敏感性,敏感性分析结果见表1。

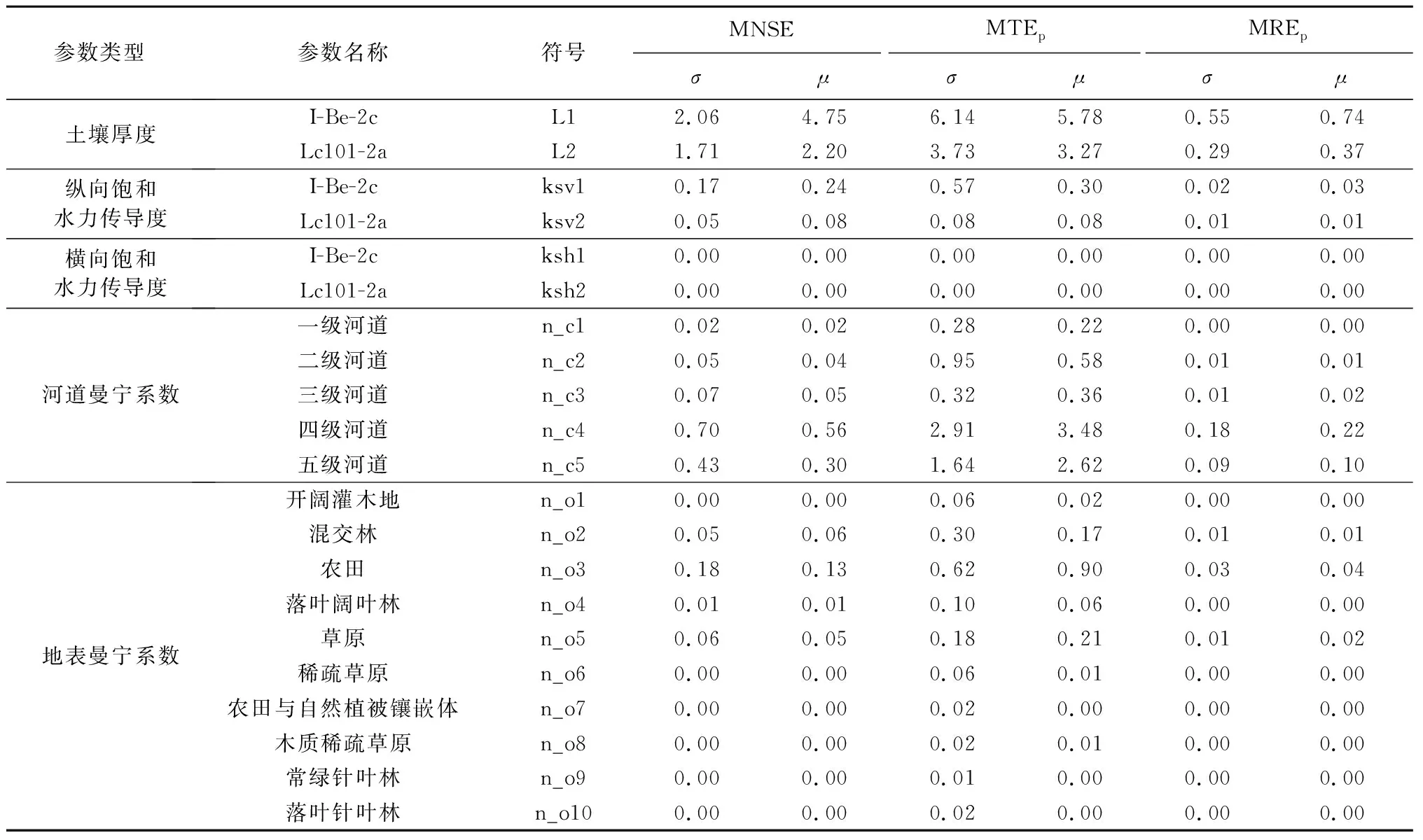
表1 敏感性分析结果Table 1 Sensitivity analysis results

可以看到影响3个目标函数的敏感参数具有高度相似性,土壤厚度为最敏感的一类参数,其次为汇流参数中的河道曼宁系数,主要是四级和五级河道的曼宁系数影响较大,土壤横、纵向水力传导度对目标函数也有一定的影响,地表曼宁系数中存在部分类别对峰现时间误差有一定的影响。综合上述结果,选取影响最大的12个参数进行参数率定,分别为L1、L2、ksv1、ksv2、n_c1、n_c2、n_c3、n_c4、n_c5、n_o2、n_o3、n_o5。

2.5 参数率定结果

从临沂流域2011—2021年资料中选取15场洪水进行模拟分析,其中前10场洪水为率定期,后5场为验证期。考虑到计算机的运行效率,3种多目标优化方法均驱动原始模型(TOPKAPI模型)5400次,不同参数优化方法得到Pareto前沿如图5所示。

图5 NSGA-Ⅱ、NSGA-Ⅲ和MO-ASMO算法的Pareto前沿Fig.5 Pareto frontiers of NSGA-Ⅱ, NSGA-Ⅲ and MO-ASMO

由图5～7和表2知,验证期MNSE效果普遍比率定期好,原因可能是率定期的10场洪水中出现个别模拟较差的场次,从而拉低了率定期的MNSE,验证期MREp与MTEp比率定期稍差。验证期MO-ASMO算法和NSGA-Ⅲ表现各有优劣,MTEp评价指标方面,NSGA-Ⅲ得到更好更集中的Pareto前沿,而MNSE和MREp方面,MO-ASMO算法表现更好。综合来看,在TOPKAPI模型中,MO-ASMO算法比NSGA-Ⅱ和NSGA-Ⅲ能取得更好效果。NSGA-Ⅲ和MO-ASMO算法各项指标均优于NSGA-Ⅱ,原因是NSGA-Ⅲ增加了参考点机制,从而导致样本点分布更分散,自变量多样性增加,从而更容易得到全局最优解。

图6 率定期3种算法目标函数比较Fig.6 Comparison of objective functions of three algorithms in calibration period

图7 验证期3种算法目标函数比较Fig.7 Comparison of objective functions of three algorithms in verification period

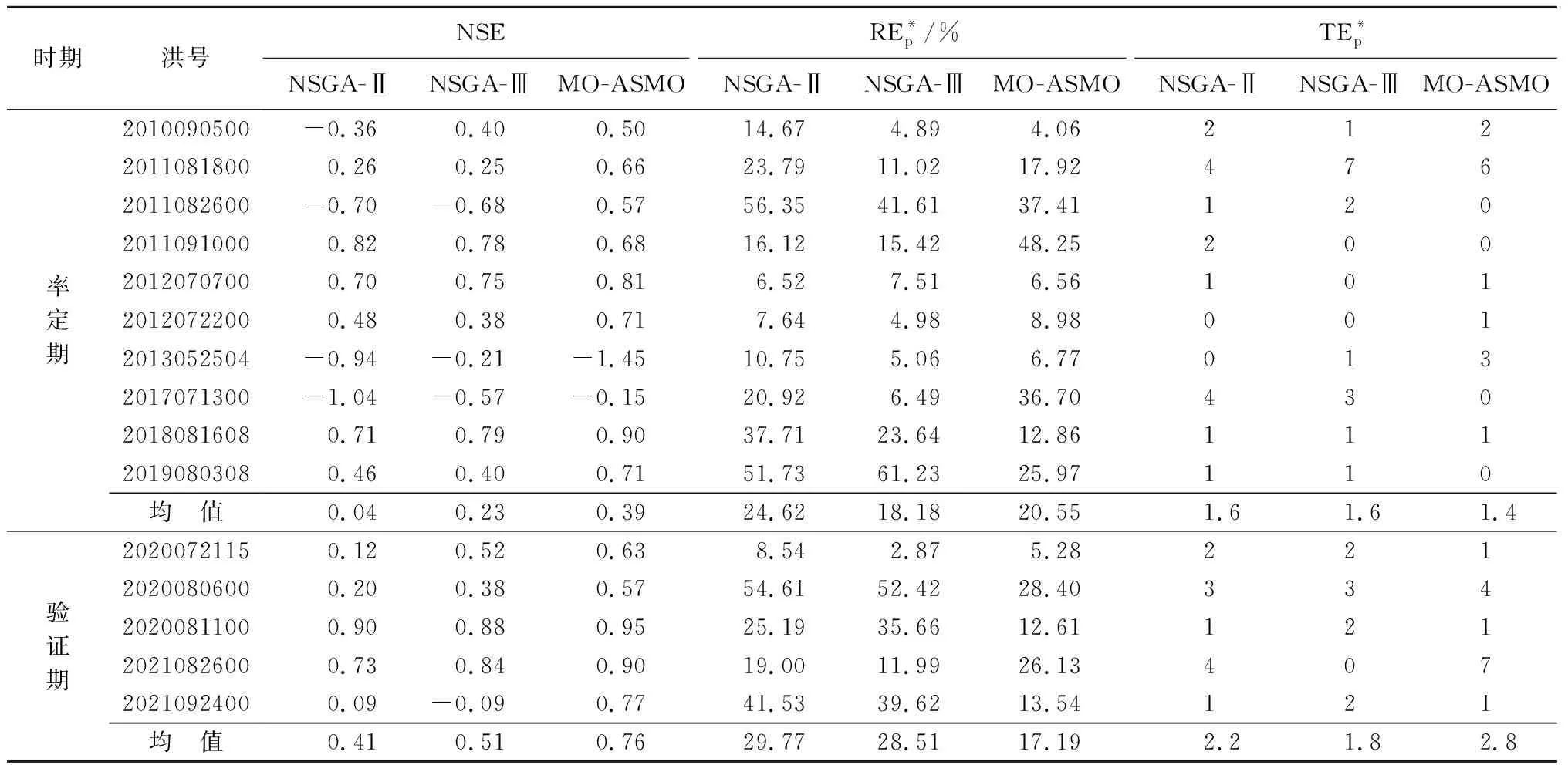
表2 3种算法目标函数对比Table 2 Comparison of objective functions of three algorithms

考虑到3种多目标优化算法得到Pareto解集个数不一致,本文对每个Pareto解集进行归一化,再求其最小欧几里得距离得到一组参数作为各个方法的最终参数,运行TOPKAPI模型得到不同方法每场洪水的目标函数值(表2)。率定期10场洪水,NSGA-Ⅱ、NSGA-Ⅲ和MO-ASMO算法的洪峰合格率分别为50%、70%和60%,峰现时间合格率为60%,70%和70%;验证期5场洪峰合格率分别为40%,40%和60%,峰现时间合格率为40%,20%和60%,MO-ASMO算法在率定期和验证期对洪峰误差的控制较好,峰现时间误差也合格,综合看比其他2种方法更优。图8为部分洪水实测与模拟结果对比,3种不同率定方法下各场洪水模拟与实测过程线在低水阶段较吻合,高水处出现不同程度偏差,总体来说MO-ASMO算法结果较好,其中2012070700号洪水第一个峰3种方法模拟均偏大,原因为TOPKAPI模型退水时间较长,洪水后期的降雨直接转化为径流,从而导致峰值模拟偏大。

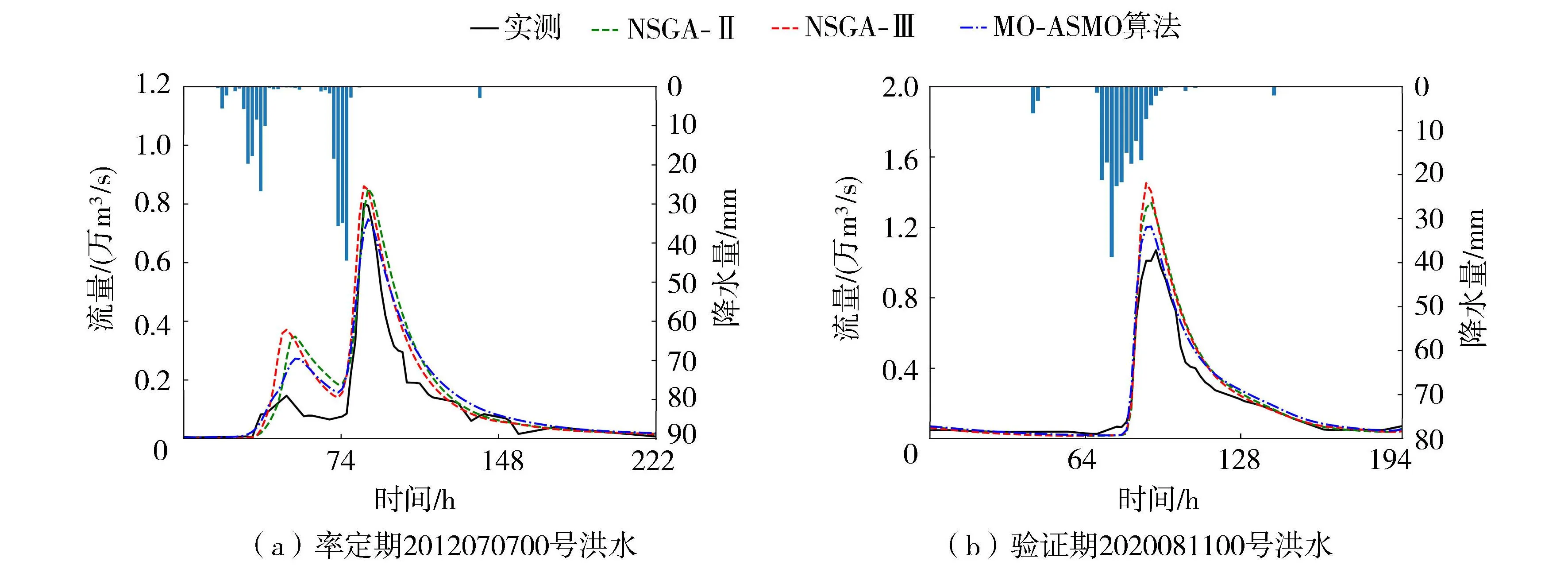
图8 部分洪水实测与模拟结果对比Fig.8 Comparison of partial measured floods and simulated results

3 结 语

为提高复杂水文模型参数优化效率,通过Morris敏感性分析方法成功筛选出12个敏感性参数,减少了参与率定的参数个数。在多目标参数优化方面,将多目标自适应代理模型优化(MO-ASMO)算法应用在TOPKAPI模型的参数率定中,对比NSGA-Ⅱ和NSGA-Ⅲ算法,MO-ASMO算法在相同模型运行次数下产生更好的Pareto前沿。通过分析相对最优解的模拟结果,MO-ASMO算法在各项指标均取得较高的合格率,有效提高了模型参数优化的效率,验证了该方法的适用性。但本文仅从模型参数率定方面探究其对模拟结果的影响,实际流域的情况比模拟复杂许多,下一步的研究中,需要考虑流域的实时变化,深入探讨代理模型在水文模型中参数实时校正等问题。