混沌系统的有限时间间歇模糊同步控制

2024-01-23闫丽宏胡鹏超陈西西

物联网技术 2024年1期

闫丽宏，陈楠，石磊，胡鹏超，陈西西，张娜

（1.咸阳师范学院数学与统计学院，陕西咸阳 712000；2.延安大学数学与计算机科学学院，陕西延安 716000）

0 引言

众所周知，混沌是一个存在于自然界和工程领域的典型非线性动力系统。一般地，当研究非线性动力系统时，遵循由确定系统到随机系统再到不确定系统的研究思路。对于确定和随机混沌系统，许多学者从不同角度进行了深入研究，并取得了相应成果，如混沌模型构造[1-2]、混沌性质刻画与分析[3-4]、混沌控制与同步[5-7]。但是，对于不确定混沌系统同步控制的研究仍较少。

T-S 模糊理论是解决不确定复杂系统甚至是病态非线性动态系统[8-10]建模和控制方面问题的非常有效的方法。通过T-S 模糊理论，可以将非线性混沌系统转化为含有非线性系数的线性系统，进而实现系统的性能分析与控制[11-13]。同时可以将模糊控制理论应用到混沌系统的同步控制中，主要包括基于模糊的控制[14-16]、自适应模糊同步控制[17-19]、脉冲模糊控制[20]、模糊滑模控制[21]、模糊间歇同步控制等[22]。间歇控制方法基于受控系统状态，将控制作用间歇地作用到受控系统中，可以节约控制成本，提高控制效率，目前在复杂动态网络等非线性系统的同步控制中得到应用。

基于以上考虑，本文针对一类低维的非自治混沌系统，通过理论分析和数值模拟，阐述基于T-S 模糊理论与自适应反馈控制策略实现耦合混沌系统同步的基本思想。

1 问题描述

考虑如下混沌驱动系统：

式中：x=(x1,x2,...,xn)T∈Rn表示驱动系统的状态；A∈Rn×n是线性参数矩阵；f(x(t))是混沌系统的非线性部分。

相应的响应系统为：

式中：y=(y1,y2,...,yn)T∈Rn表示混沌响应系统的状态向量；u(t)是待设计的外部控制器。

这里采用如下的模糊规则：

规则l：θi(t)是第i个节点的先验变量，i=1, 2,...,m；Flm是具有隶属函数特征的模糊集。如果θ1是Fl1，θ2是Fl2,...,θm是Flm，那么：

式中：r是IF-THEN 规则的数量；Al∈R3×3是模糊矩阵。采用标准的模糊推理方法，通过单点模糊推理、乘积模糊推理和中心平均去模糊法，模糊混沌系统可以推导成如下形式：

式中：θ(t) =[θ1(t),θ2(t), ⋅⋅⋅,θm(t)]；；。

模糊权函数μl(θ(t))满足：

同步误差为：

式中，e(t)=(e1(t),e2(t),...,en(t))T。

在模糊规则l(l=1, 2,...,r)下，误差系统为：

式中，u(t)是待设计的有限时间间歇控制器。

如果θ1是Fl1，θ2是Fl2,...,θm是Flm，那么：

式中，对角矩阵Kl是正的控制增益矩阵，l=1, 2,...,r。参数ζ>0 是可调实常数，实数α满足0<α<1，T>0 是控制周期，δ>0 是控制宽度，m∈Z/Z-。向量sgn(e(t))|e(t)|α=(sgn(e1)|e1|α,sgn(e2)|e2|α,..., sgn(en)|en|α)T。

控制器设计如下：

将模糊控制器设计公式（9）代入到误差系统公式（7）中，可以推导出模糊控制系统公式（10）的T-S 模型。

为了进一步讨论方便，首先介绍如下引理。

引理1[20]：假设连续正定函数V(t)满足如下微分不等式：

式中，常数α>0，0<ε<1，那么对于任意给定t0，V(t)满足如下不等式：

式中：

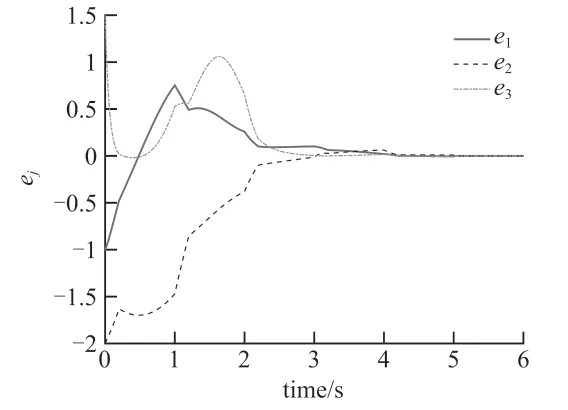
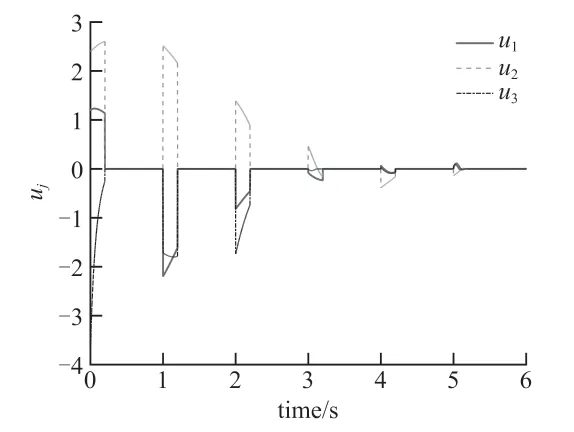
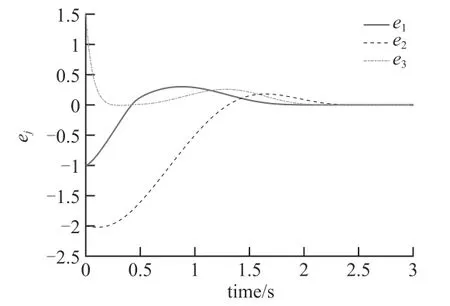
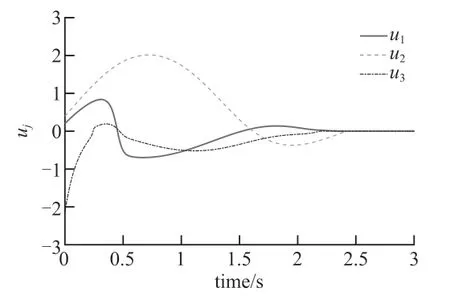
引理2[21]：如果x1,x2,...,xn是任意整数，0

引理3[22]：假设连续正定函数V(t)满足如下微分不等式：

式中，0<ε<1，I>0，κ>0，那么驻留时间t2满足：

引理4[23]：假设函数V(t)在t∈[0, ∞)是连续且非负的，并且满足如下条件：

式中，α，β>0，T>0，0<η，θ<0，那么如下不等式成立：

2 模糊间歇同步控制

本节将给出驱动-响应混沌系统式（1）和式（2）实现有限时间同步的结论。

定理1：假设存在正定对角矩阵Kl使得如下不等式成立：

那么在控制器设计公式（9）的作用下，驱动-响应混沌系统式（1）和式（2）在时间tf内可以实现有限时间同步，则有：

证明：构造如下Lyapunov 函数：

情形1：当mT≤t

所以：

其中，sym(Al)=Al+AlT，sym(Kl)=Kl+KlT。根据引理2，则有：

所以：

根据式（19）的条件，则有：

情形2：当mT+δT≤t

简化上述方程可得：

结合式（27）和式（29），可得：

根据引理3，则有：

结合引理4，可得：

证毕。

值得注意的是，如果控制宽度δ=1，那么间歇控制器简化为连续控制输入，有如下推论。

推论1：假设存在正定对角矩阵Kl使得如下不等式成立：

那么利用控制器设计公式（9）和驱动-响应混沌系统式（1）和式（2）在时间te内实现有限时间同步，则有：

3 数值仿真

本节中，我们将利用数值计算说明驱动-响应混沌系统式（1）和式（2）的有限时间同步控制结论。不失一般性，选择Chen 混沌系统进行仿真。

当参数α=0.2、β=5.7 时，系统是混沌的。选择x1、x3作为观测变量，通过计算，可知变量x1和x3的取值区间分别是[-9.2 11.5]和[0.01 22.96]。矩阵Ai，i=1, 2 分别表示为：

进一步，特征值分别为：λmax(sym(A1))=0.039 1，λmax(sym(A2))=28.504 2，所以可知λA=28.504 2。根据条件式（19），反馈矩阵分别取为：K1=diag{29 0.6 0.3}，K2=diag{28.6 0.3 0.2}；模糊权函数μl(θ(t))在l=1, 2 时分别为：μ1(θ(t))=(1+2 sin2t)/3，μ2(θ(t))=2 cos2t/3。调节因子ζ=1.5，正指数α=0.5。仿真过程中，间歇控制器设计公式（9）的参数分别取为：T=1，δ=0.2。系统初始条件为：x(0)=[2 -1 3]，y(0)=[1 -3 4.5]，迭代步长h=0.000 1。

数值仿真结果如图1 ～图6 所示。图1 展示了驱动-响应系统的同步误差演化过程，可以看到系统的状态在有限时间内趋于0，这与理论分析结果一致。图2 是模糊周期间歇控制器的状态，该控制器在有限时间内稳定到0。而且，当增加反馈控制增益的值由K1=diag{30 2 1}到K2=diag{29.6 1.3 1.2}时，通过仿真发现，反馈增益越大，实现同步的时间越短。仿真结果如图3 和图4 所示。