包装件随机振动时域响应和PSD 快速获取方法研究
2024-01-23薛阳宋卫生
薛阳,宋卫生
(河南牧业经济学院,河南 郑州 450046)
在公路运输环节,货物(包装件)受到的激励主要是随机振动,来自运输工具(车辆)底板。要深入地分析包装件或包装件内易损零部件的振动行为,需要得到包装件或易损件的振动响应和其功率谱密度(PSD)。目前有两种方法可以实现,分别是从试验和仿真分析的角度出发。
试验方法是将加速度传感器固定在包装件指定位置上,记录运输环节包装件的加速度时域信号,然后将采集到的时域信号转换成加速度功率谱密度。也可以将随机振动记录仪固定在车辆底板指定位置上,采集车辆底板的加速度时域信号,转换成加速度功率谱密度后在随机振动试验台上复现,而后利用随机振动试验台获取包装件的振动响应和功率谱密度[1]。试验方法操作简单,精度高,但耗时长,成本较高。
仿真分析方法是首先建立路面不平度模型,生成路面对车辆的激励;建立车辆的多自由度振动模型,得到车辆底板即包装件底部的振动响应,该响应即为包装件受到的振动激励;根据实际情况建立包装件的单自由度/多自由度或者非线性振动模型,最后得到其振动响应和功率谱密度[2]。仿真分析方法耗时非常短,精度相对较高,但对操作者的理论水平和数值计算程序编写能力要求较高。基于仿真分析方法的以上优缺点,本文意图清晰地梳理整个设计过程,并结合相应程序进行介绍。
1 路面不平度模型构建
1.1 路面频域模型
国家标准GB 7031 建议采用路面频域模型即功率谱密度来描述路面不平度,如下所示:
式中,和分别是参考空间频率和空间频率,单位是,,是谱密度指数,一般设置为2,和分别表示对应空间频率下的路面位移谱密度,单位为,也称为路面不平度系数。
为了方便地研究车辆与包装件的振动特性,常常需要将路面不平度的频域模型转换成时域模型,其中常用的方法是滤波白噪声生成法[3]。
1.2 路面时域模型
利用滤波白噪声生成法可以建立路面不平度的时域模型,如下所示:
式中,是路面受到的随机激励,为车辆速度,单位是m/s,是零均值白噪声过程,其方差,和是对应路面等级下的常数[4]。
基于上述分析,可基于Matlab 软件的Simulink仿真模块建立路面对四轮车辆输入的时域仿真模型[5],如图1 所示。
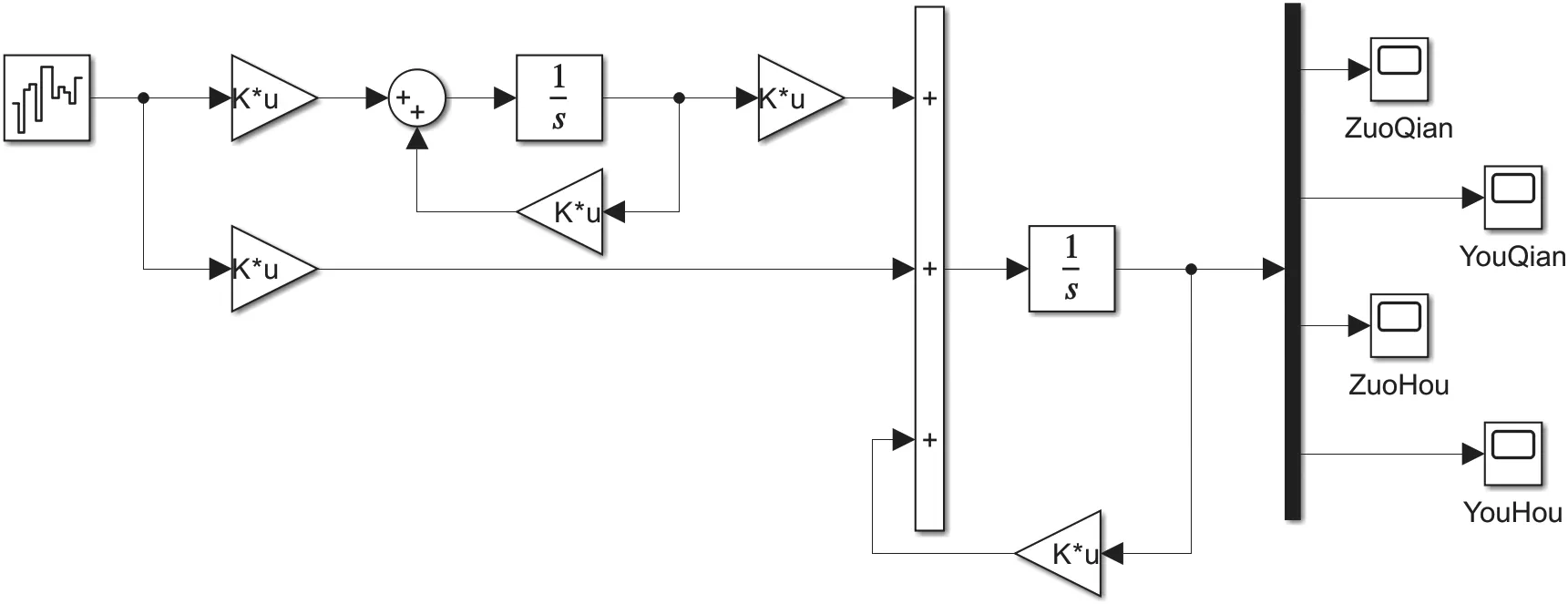
图1 路面对四轮车辆输入的时域Simulink 仿真模型
2 四轮车辆振动模型构建
基于拉格朗日方程,可以建立多自由度运输车辆的振动方程[2,4]:
其中,分别是系统的质量、刚度和阻尼矩阵,是车辆的位移响应列向量,是轮胎刚度矩阵,是路面对车辆前后四轮随机激励的列向量。
为了方便地使用Simulink 仿真模块对上述模型进行求解,可以用状态空间表达式对振动方程进行转换,进而得到车辆底板的时域响应。假设车辆速度为15m/s,行驶在C 级路面上,仿真时间设置为50s,则四轮车辆底板的位移响应、加速度响应如图2 所示,加速度均方根值为0.1739g。加速度功率谱密度可以使用Welch 平均周期图法来进行绘制,在Matlab 软件中的调用函数是pwelch( ),计算得到的加速度功率谱总均方根值为0.1739g。

图2 四轮车辆底板的位移和加速度响应
3 包装件振动模型构建
在上一部分,已经介绍如何获得四轮车辆底板的时域响应。建立好包装件振动模型,将四轮车辆底板的响应作为包装件的输入,可通过计算得到包装件的振动响应。如果包装件是单自由度/多自由度线性振动模型,可以用上一部分的状态空间表达式对包装件的振动方程进行处理。
如果包装件是非线性振动系统,比如包装件内缓冲材料是三次非线性或者包装件内易损零部件需要看作是简支梁式/悬臂梁式结构的情况,笔者建议包装件的模型求解部分使用自写程序的方式来解决。因为Simulink 仿真模型自带的state-space 在continues模块组下只能描述线性系统。接下来以二自由度非线性包装件为研究对象介绍后续程序如何设计。
二自由度包装件系统模型如图3 所示,其中m1是易损零部件的质量,m2为除易损件外包装件主体的质量。假设易损件与主体连接部分的弹性力是线性,包装件主体与车辆底板之间缓冲材料的弹性力为三次非线性,表达式为F(x)=k2x+rx3,k2是初始弹性系数,r 是非线性常数,c1和c2是相应部分的阻尼,u 是四轮车辆底板的随机位移激励,已经在上一部分完成求解。对于此二自由度振动问题,可以以易损件静平衡位置处为坐标原点,建立坐标系x1,以包装件主体静平衡位置处为坐标原点,建立坐标系x2,两个坐标系都以向上为正方向,可建立系统的动力学方程:
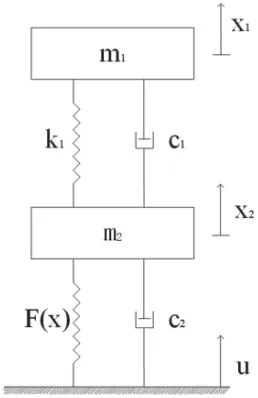
图3 二自由度包装件系统模型
接下来可以用龙格库塔数值算法对式4 的动力学方程进行求解,需要注意的是,由于系统的外部随机激励u和不能用一个关于时间的函数表示,因此需要对u和进行插值处理,找到任意时刻t 对应的值。程序设计如下所示:
y0=[0;0;0;0];%易损件与包装件主体的初位移和初速度
tspan = u(:,1);%计算时间跨度
[TT, Y] = ode45(@ (t, y) odefun_2(t, y, k1,k2, c1, c2, m1, m2, r, u, du), tspan, y0);
function dydt = odefun_2(t, y, k1, k2, c1,c2, m1, m2, r, u, du)
dydt = zeros(4,1);
dydt(1) = y(3);
dydt(2) = y(4);
%对位移激励做一个插值
Ut = interp1(u(:,1), u(:,2) , t, ‘spline’);
dut = interp1(u(:,1), du, t, ‘spline’);
dydt(3) = (k1/m1)*(y(2) - y(1)) + (c1/m1)*(y(4)- y(3));
dydt(4) = (k2/m2)*(ut - y(2)) + r*(ut -y(2))^3 + ...
(c2/m2)*(dut - y(4)) - (k1/m2)*(y(2) - y(1)) -(c1/m2)*(y(4) - y(3));
end
运行上述代码后,可以得到包装件主体以及易损件的位移响应,如图4 所示。
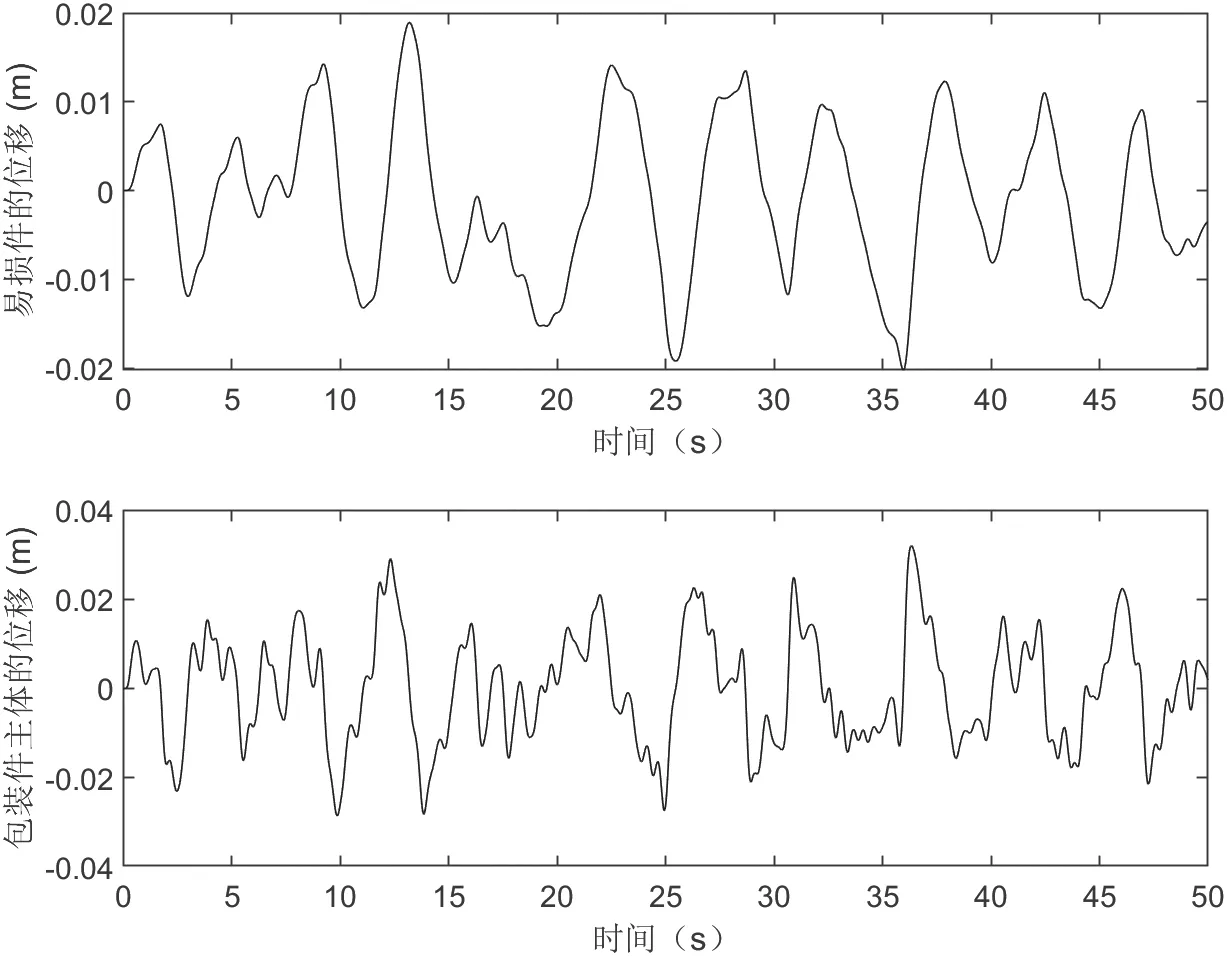
图4 包装件主体和易损件的位移响应
易损件和包装件主体的加速度响应可通过下面代码计算,结果如图5 所示。计算各自的加速度均方根值分别是0.0037g 和0.0042g。
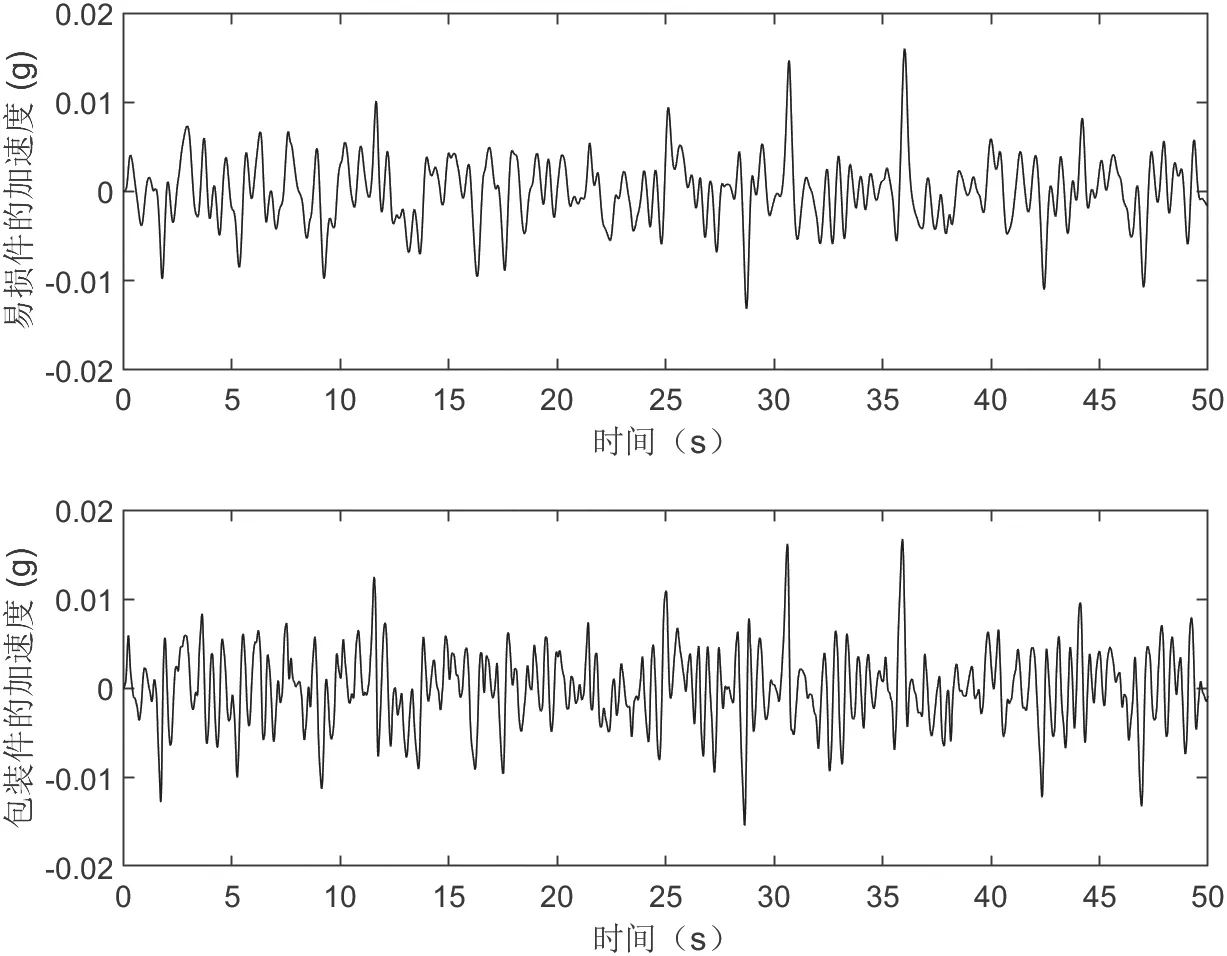
图5 包装件主体和易损件的加速度响应
%输出每个时刻易损件的加速度ddXX1
ddXX1 = (k1/m1)*(Y(:,2) - Y(:,1)) + (c1/m1)*(Y(:,4) - Y(:,3));
ddXX1 = ddXX1/g;
disp ([‘易损件的加速度均方根值为 ‘ num2str(rms(ddXX1)) ‘ g’]);
dut = interp1 (u(:,1), du, TT, ‘spline’);
ut = interp1 (u(:,1), u(:,2) , TT, ‘spline’);
%输出每个时刻包装件的加速度 ddXX2
ddXX2 = (k2/m2)*(ut - Y(:,2)) + r*(ut -Y(:,2)).^3 + ...
(c2/m2)*(dut - Y(:,4)) - (k1/m2)*(Y(:,2) -Y(:,1) ) - (c1/m2)*(Y(:,4) - Y(:,3));
ddXX2= ddXX2/g;
disp([‘包装件加速度均方根值为 ‘ num2str(rms( ddXX2)) ‘ g’ ]);
使用平均周期图法可以计算易损件的加速度功率谱密度,具体代码如下。计算结果如图6 所示。计算得到的加速度功率谱密度总均方根值为0.0038g,与车辆底板相比,随机振动强度大幅减弱,说明缓冲包装可以有效地保护易损零部件。

图6 易损件的加速度功率谱密度
xn = ddXX1;
nfft = 1024;
noverlap = 20; %数据无重叠
window = boxcar(100); %矩形窗
[pwelchx,Fxx] = pwelch (xn, window, 20,nfft, Fs, ‘psd’);
plot(Fxx,pwelchx);
P S D_G r m s_p w e l c h x = C a l_P S D_Grms(Fxx,pwelchx); %计算功率谱密度的总均方根值
disp([‘平均周期法PSD 的总均方根值为 ‘num2str(PSD_Grms_pwelchx) ‘ g’]);
xlabel(‘频率(Hz)’); ylabel(‘易损件加速度功率谱密度(g^2/Hz)’);
set(gca,’yscale’,’log’);%取对数实现纵坐标不均匀分布set(gca,’xscale’,’log’);%取对数实现纵坐标不均匀分布
xlim([0 200])
4 结语
本文较为详细地从仿真角度介绍了如何快速计算公路运输过程包装件随机振动时域响应和功率谱密度的方法,并且给出了相关程序。上述程序适用于非线性包装件振动模型,对于易损件为简支梁或悬臂梁结构,可以运用有限差分法对模型进行求解。由于篇幅有限,笔者在这里不过多赘述。希望本文可以为相关研究者提供一些参考,同时为包装工程本科生学习运输包装课程时提供一些帮助,加深对包装件随机振动的认识。
