基于梯度提升的优化集成机器学习算法对滑坡易发性评价:以雅鲁藏布江与尼洋河两岸为例
2024-01-22林琴郭永刚吴升杰臧烨祺王国闻
林琴,郭永刚,吴升杰,臧烨祺,王国闻
(西藏农牧学院水利土木工程学院,西藏 林芝 860000)
雅鲁藏布江与尼洋河位于青藏高原东南部,盆地内山脉纵横起伏,形成大量冲沟、峡谷和河流。内部动力作用非常活跃,地壳中初始高压应力释放,盆地岩石结构松弛。崩塌、滑坡和泥石流等自然灾害频繁发生(苏立彬,2020;武辰爽,2021)。滑坡是自然和人类活动引起的对土壤的破坏(Taalab et al.,2018)。它是一种以大量岩石、碎屑或泥土向坡面移动为特征的自然灾害。无论是由自然还是人类活动造成的滑坡,每年都会造成重大的经济损失(Tien et al.,2018)。因此,利用高效稳定的滑坡灾害评估技术,针对滑坡易发区,快速准确地识别高易发区的灾害,预测滑坡灾害的发生,可以有效地提高灾害预测的效率,减少滑坡灾害造成的损失,为防灾减灾提供参考(张琪等,2023;周硼焜等,2023)。
滑坡易发性划区是通过滑坡发生后的影响因子属性来预测滑坡发生的概率,是滑坡预测的有效方法(沈玲玲等,2016;孟晓捷等,2022)。滑坡易发性评价通常采用传统的定性方法和定量方法(贾俊等,2023)。定性方法依赖于专家在历史资料和滑坡清单的经验和意见,如加权线性组合与层次分析法(Rehman et al.,2022),但计算结果受人为因素影响。定量方法包括数据模型和确定性模型。确定性模型可以提供精确的分析结果,但需要大量的数据,尤其是在大尺度地区实践中难以获得(杨创奇等,2022)。近年来,包括机器学习和统计学的数据驱动模型在地质灾害研究方面取得了显著进展,如证据权模型(WoE)(Batar et al.,2021)、频率比(FR)(Khan et al.,2019)和确定性系数法(CF)(乔德京等,2020)等。这些算法计算简便,甚至在一些大型区域也能适用,但是过分依赖样本质量且无法有效处理复杂的滑坡及其影响因子之间的关系。机器学习中的随机森林(Arabameri et al.,2019)、决策树(Hong et al.,2018)、BP神经网络(康孟羽等,2022;张林梵等,2022)、梯度提升等也被广泛地运用在滑坡识别中(张文龙等,2023),较好地解决了非线性关系表达的问题,提高了滑坡识别的精度。然而,这些模型通常依赖于单一的学习器,滑坡易发性所涉及的影响因子众多,通常很难获得理想的预测结果,容易发生过拟合现象。因此,笔者利用集成学习将多个单学习器组合起来进行区域滑坡易发性评估,以比较其与传统方法更具有优越性和高效性。
近年来,大量基于机器学习的方法被成功应用于地质灾害研究,而较新的梯度提升(Boosting)模型,包括XGBoost 和LightGBM 模型,在滑坡易发性方面很少被研究与比较,且不平衡类分布可能会影响特征选择的假设。在此基础上,笔者以雅鲁藏布江与尼洋河两岸为例,首次引入了基于基尼系数的加权随机森林作为特征选择过程过程,并与基于Boosting 算法的XGBoost和LightGBM 模型对研究区滑坡易发性进行分析和比较。
1 研究区与数据
1.1 研究区
笔者选取雅鲁藏布江下游与尼洋河两岸为研究对象(图1)。研究区位于西藏自治区林芝市西部,E 92°09′~95°51′,N 27°55′~30°36′,总面积约为68 000 km2,包括工布江达县、波密县、米林县、朗县、墨脱县。研究区属于典型的高原丘陵、高山峡谷地貌,是世界陆地垂直地貌落差最大的地带,区内地形起伏大,呈现北高南低走势,山脉多为东西走向,绝大多数为高海拔大起伏山地,其次为高海拔极大起伏山地与中高海拔极大起伏山地,最高海拔7 782 m,地处米林县与墨脱县的交界地带。研究区位于高原温带湿润半湿润季风区气候带寒带跨越到热带。地区水汽含量高,雨季开始得早,结束晚,持续时间长,年平均降水量约为650 mm,年平均气温为9.1 ℃。研究区内有日土-青丁断裂、达机翁-朗县断裂、贾桑断裂、札达-邛多断裂等断裂带,主要出露底层有盆地相上三叠统的砂岩、夹板岩、火山岩以及海相下—中三叠统的千枚岩、砂岩、含砾状灰岩等。由于高降雨量以及土壤和板块内动力活跃,该区域极易发生滑坡。

图1 研究区地理位置及滑坡分布Fig.1 Geographical location and landslide distribution of the study area
1.2 数据来源与处理
主要数据来源包括:①地理空间数据云的ASTER GDEM 30 m 分辨率数字高程数据,基于ArcGIS 软件对坡度信息进行了提取。②1∶5 万地质图来源于中国地质调查局,用来提取地层岩性性质。③Landsat8影像来源于地理国情普查,用于土地利用数据的提取。④滑坡数据出自中国科学院资源环境科学数据中心。⑤断层带从地震活动断层探察数据中心获取。
笔者在已有的研究方法上将30 m×30 m 栅格大小设定为基础的评价单元(Tanyas et al.,2019),研究区域划分为123 156 296 个网格。同时为了解决样本不均衡问题,笔者采用下采样方式从非滑坡区选取等量滑坡点组成188 个样本点(Polykretis et al.,2018),滑坡单元设为1,非滑坡单元设为0,从中随机抽取70%(131)数据作为训练样本,剩余30%(57)作为测试样本。滑坡点具体流程见图2。

图2 流程图Fig.2 Flow Chart
2 评价因子选取与独立性检验
2.1 评价因子选取
已有对雅鲁藏布江流域的研究结果和现场勘查表明:河水对河谷的不断侵蚀作用加上高海拔高寒区冻融加剧滑坡区岩石的风化,使得雅鲁藏布江流域极易孕育滑坡(赵永辉,2019);地层岩性是滑坡产生的重要因素(赵永辉,2021);坡度为滑坡发生的主控因素(王瑞琪等,2019)。再根据对研究区的地质灾害形成条件与地质环境背景研究分析,选取高程、坡度、断裂带与断层、河流、道路、地层岩性、土地利用7 个评价因子。利用ArcGIS 软件,将高程、坡度、地层岩性、土地利用4 个连续型因子结合分布规范,采用自然间断法将研究区分为5 个等级(图3a~图3d),对于离散型因子例如断裂带与断层、河流、道路利用多环缓冲区工具建立0~200、200~400、400~600、600~800、>800 m 共5 个等级范围(图3e~图3g)。
统计各评价因子分级范围内滑坡点数量并绘制蔟类柱状图(图4)。结果表明:当高程处在32~1 544 m时,滑坡发生的最多,占总数的30.9%,其次是出现在2 722~3 752 m 范围内。其原因是在海拔低于1 544 m时,开挖坡脚等人类活动频繁,随着海拔的提升,坡度增大,加剧了滑坡的发生;随着坡度上升,滑坡数也增加,直到坡度上升达到阈值40°,发生灾害的概率降低,由原来的41.5%逐渐降低到16.0%;当地层岩性为雅鲁藏布江带闪片岩时,相比其他岩性,滑坡发生最频繁;草地土壤侵蚀严重,是浅层滑坡的重要原因。本研究中大量滑坡点分布在坡度为10°~20°的草地上;断裂带与断层会降低岩层的强度和完整性,是滑坡易发性增大的关键,在距断层带200 m 以内容易发生滑坡,滑坡点占总数的41.5%,离断裂带与断层越远滑坡灾害越少;河岸受水流不断冲刷,土石在地下水及重力作用下越发失稳,因此越靠近河流越容易发生滑坡,滑坡在距河流200 m 以内,发生次数最多,达到40.4%;修建铁路、公路时因大力爆破、强行开挖,常使坡体下部失去支撑而发生下滑,距离道路200 m 以内的滑坡数占了总数一半以上达到52.1%,距离道路越远,滑坡活动减少。文中结论与相关研究均吻合(Kouhartsiouk et al.,2021;Zweifel et al.,2021)。
2.2 评价因子独立性检验
为了研究各评价因素的相对独立性以及评价模型的准确性和可靠性,笔者采用皮尔逊相关系数计算影响评价因子的相关性。皮尔逊相关系数是用于度量两个变量之间的线性关系,利用两个变量间的协方差和变量的标准差进行计算而来(Lee et al.,2020)。
式中:X,Y表示变量,N表示取值个数。
变量间呈现极弱相关时,相关系数为0.0~0.2;0.2~0.4 表示变量之间弱相关性。将评价因子的7 个属性值代入式(1)计算,结果见表1,发现相关性最高为坡度与道路(R=0.349 3),其他变量间相关关系均小于0.4。总体而言,变量的共线性不强。

表1 因子间皮尔逊相关系数表Tab.1 Pearson correlation coefficient between factors
3 雅鲁藏布江与尼洋河两岸滑坡易发性评价
3.1 基于Gini-RF 的滑坡易发性评价
随机森林(Random Forest)是一种基于决策树模型的Bagging(Bootstrap AGgregation)的优化版,由于其具有对特征鲁棒性强、适用于高维稠密性数据、并行集成、对不平衡的数据集可自动调整误差、微调超参数等优势,可以获得准确结果,常被用于各种分类和回归任务(Alsahaf et al.,2018)。它的基本单元是决策树,但其本质是集成学习方法,是机器学习的一个分支,其核心思想始终为Bagging。然而,已经做了一些特有的改进,随机森林使用CART 决策树作为基学习器。
基于Gini 系数的随机森林建立在许多决策树上并支持各种特征权重度量。其中之一为特征与不平衡数据输出的相关性,一旦分类器测量了Gini 系数,这种特征选择技术就在 RF 中采用了权重调整技术。Gini 指数具有在特定节点中划分二进制类的能力(Disha et al.,2022)。对于具有两个以上不同值的属性,考虑属性子集,通过调整不平衡类分布的随机森林算法中的权重,使用Gini 系数标准来分裂树,计算特征重要性得分。GI 值越高,特征对模型预测的平均贡献越大,模型的解释能力越好,所有GI 特性之和为1。
公式(2):GIm为基尼指数,K代表k个类别,pmk表示节点m中k的比例;公式(3):表示特征i在第j颗树的权重;公式(4)表示对所求出的所有重要度得分进行归一化处理。
笔者把94 个滑坡点记为‘1’,等量非滑坡点记为‘0’,将7 个评价指标因子的属性提取至训练集,构造随机森林二分类模型,并从sklearn 库中调用Random Forest Classifier 方法,将训练集代入RF 模型进行训练。同时为了确保结果的可靠性和准确性,在原本的参数设定基础上,采用贝叶斯优化算法搜索最优参数值。优化结果中,当每次迭代完成后更新权重时的步长取0.1,max_depth 取4,num round 取30 时,效果最佳。用测试集对RF 模型进行预测,结合公式(3),将得到各评价因子的权重归一化后导入ArcGIS 中的栅格计算器生成滑坡易发性图,采用自然间断法将分区图划分为极高、高、中、低、极低5 个等级(图5),易发性越高代表越容易发生滑坡。

图5 Gini-RF 模型滑坡易发性分区图Fig.5 Susceptibility zoning map of Gini-RF
3.2 XGBoost 易发性评价
XGBoost 是一种基于决策树模型和梯度提升的集成机器学习算法,为了控制模型的复杂度,它将正则化项添加到损失函数中,正则项包括每个叶子节点权重的平方和与节点个数。XGBoost 处理缺失值并通过学习模型选取缺失值最佳的默认分割方向(Inan et al.,2021)。
描述的数据在预处理过程之后,基于Python3.6与R 语言,采用Scikit-learn 构建XGBoost 多分裂滑坡易发性模型(Alsahaf et al.,2018)。同时为了在独立的验证数据集上对子序列进行测试降低偶然性,选取最优子树,通过贝叶斯算法优化,利用五折交叉验证获得每个模型评价度量的平均值,所有测试集的平均指标被认为是最终结果。将预测结果导入ArcGIS 绘制滑坡易发性图(图6)。样本集在所选参数值上的交叉验证准确度结果显示:当进行第5 次五折交叉后,训练集和测试集的AUC 值达到最大值并趋于稳定(图7)。
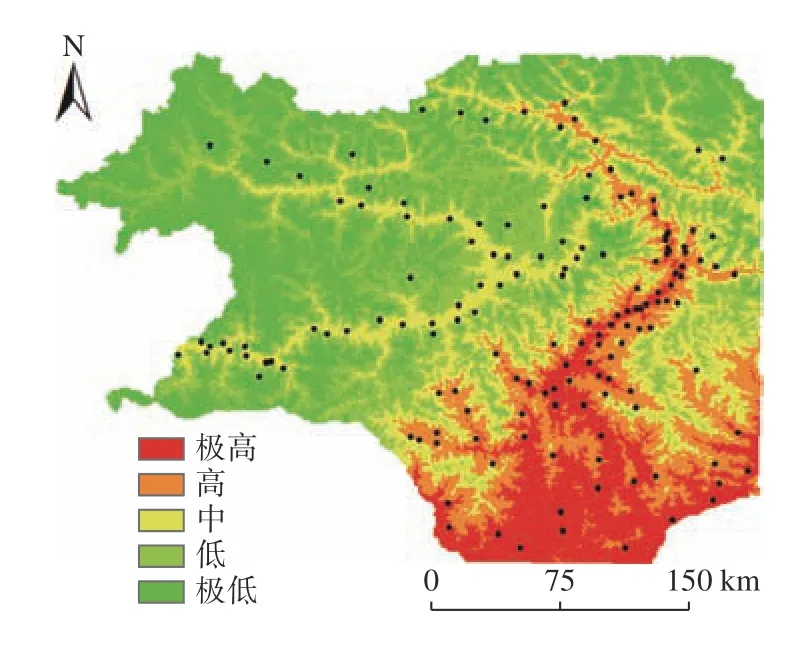
图6 基于XGBoost 的滑坡易发性图Fig.6 Susceptibility zoning map of XGBoost

图7 XGBoost 五折交叉验证结果Fig.7 XGBoost 50% ross validation results
3.3 LightGBM 易发性评价
Light Gradient Boosting Machine(LightGBM)是一种高性能、开源、快速的分类、回归、排名的方法,同时也是基于决策树算法的梯度提升算法。LightGBM采用直方图算法来降低内存消耗,使数据分割更简单,将浮点的连续特征离散化为式子中的k 个离散值,构造一个宽度为 k 的直方图,将数据进行遍历训练,计算直方图中每个离散值的累积统计信息,在特征选择中,只要根据直方图离散值搜索最佳的分割点即可(Zeng et al.,2019)。
在4.2 使用方法基础上,将研究区的123 156 296个栅格提取各评价因子的属性值到点,生成123 156 296×7的表格,导入训练好的机器学习模型中,预测每个栅格发生滑坡的概率,利用点转栅格工具将所有的点生成栅格数据,再用自然间断法将研究区的滑坡易发区分为极高、高、中、低、极低5 个类别(图8)。图9 为LightGBM 的学习曲线。

图8 基于LightGBM 的滑坡易发性图Fig.8 Susceptibility zoning map of Gini-RF
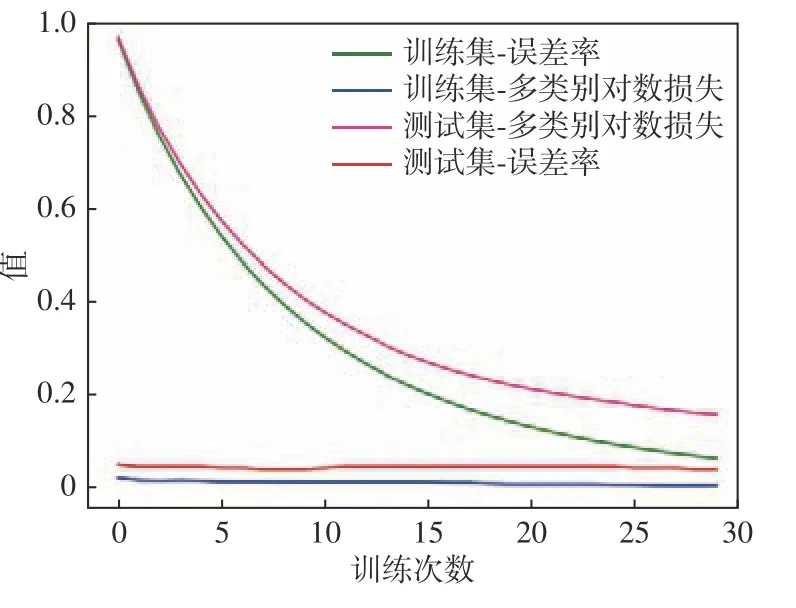
图9 LightGBM 学习曲线Fig.9 LightGBM learning curve
4 滑坡易发性评价结果验证
4.1 易发性分区结果与对比
基于ArcGIS,分别统计3 种不同机器学习模型在每个易发性分区的栅格个数与滑坡点个数(表2),3种模型的滑坡易发性结果呈现出一定的差异,但整体趋同。Gini-RF、XGBoost 和LightGBM 模型均在极低类别中的百分比值最高。对于Gini-RF 模型,从极高到极低易发性的面积比分别为11.99%、12.63%、19.58%、26.77%和29.03%。XGBoost 模型的极高、高、中、低和极低易发性区域分别占12.05%、12.50%、19.62%、26.78% 和29.05%。对于LightGBM 模型,极低、低、中、高和极高易发性区域分别占12.14%、12.41%、19.43%、26.47%和29.55%。根据滑坡位置的分布可以看出,大多数历史滑坡记录位于高易发性地区,正如Gini-RF、XGBoost 和 LightGBM 模型所预测的那样。LightGBM 模型的性能最高,其次为XGBoost 与Gini-RF。

表2 机器学习模型易发性分区对比Tab.2 Comparison of machine learning model vulnerability zones
根据评价因子的选取及易发性评价分区图可知,滑坡高和极高易发区多位于墨脱县的达木乡、帮辛乡,林芝县的丹娘、里龙、扎西饶登乡,朗县的陇村,工布江达的江达乡。在这些地区应采取相应的地质灾害防治措施。特别是位于雅鲁藏布江与尼洋河两岸海拔较低、坡度为30°~40°,距河流、道路、断裂带200 m以内的区域。
究其原因,这类地区位于雅鲁藏布江与尼洋河两岸南部与印度板块和亚欧板块交界,地壳运动剧烈,孕育一系列区域性断裂,断裂带与断层降低了岩层的完整性和强度,并且高程多位于200~1 000 m,大多数坡度小于40°,在此范围内人工多进行切坡建房和道路建设等强烈活动,造成大量的裸露斜坡,加上长期的流水作用,使河流两岸遭受严重的侵蚀和冲刷,导致沉积物饱和,从而降低斜坡的完整性,使斜坡运动或质量运动,且距道路越近,道路建设所造成的破坏性会对边坡稳定性产生负面影响,因此滑坡灾害频发。
相反,滑坡低易发区主要分布在工布江达县的错高、朱拉区,林芝市的冲果俄、港阿如,米林县的苏鲁胖地区,其特点是坡度较缓、人类活动较少,远离道路、河流、断裂带。
4.2 模型精度比较
在机器学习中,性能指标通常用于二进制分类中测试集的正确预测数。笔者使用准确度(Accuracy)、精确度(Precision)、召回率(Recall)、F1 分数、(ROC)曲线和AUC 值6 个指标对不同机器学习模型的精度进行了评价。准确度分数是评估模型在二元分类问题中的性能的最常用指标,表示在所有样本中,能被正确识别的概率;精确度是通过计算模型预测为真时实例为正样本的频率来评估模型性能的度量;召回率是模型正确检测真阳性实例的度量;F1 分数是召回率和精度之间的权衡指数,同时考虑了FP 和FN,使模型整体更具准确性。具体公式如下:
式中:TP和TN分别为真阳性和真阴性,代表正确分类的像素数;FP和FN分别是假阳性和假阴性,代表错误分类的像素数。
为了得到不同机器学习算法在测试数据集上的预测准确性,基于上述方法,利用公式(5)~公式(8)计算精确度、精确度、召回率和F1 指数,随机抽取30%样本作为测试样本,得出模型的泛化能力和准确率(表3)。可以看出,基于不同框架算法的预测性能不一样。3 种机器学习模型中,LightGBM 模型在超参数优化下其AUC(0.843 2)、ACC(0.853 1)、F1 分数(0.834 5)、Precesion(0.825 1)均高于另外两种机器学习模型。

表3 各机器学习模型准确率Tab.3 Accuracy of each machine learning model
在机器学习中,ROC 曲线被广泛应用于二分类问题中来评估分类器的可信度(张玘恺等,2020)。AUC为ROC 曲线下面积。AUC=1 表示该曲线存在至少一个阈值能得出完美预测。曲线纵轴为真阳率TPR,横轴为假阳率FPR,越靠近左上角,则认为该判断指标预测能力越好。从这条 ROC 曲线可以看出,经过网格搜索与5 折交叉验证后的蓝色曲线LightGBM 模型更接近左上角,AUC 值为0.843 2,与Gini-RF 模型的0.822 5 有较大提升,且准确率高于XGBoost 模型的0.935 8(图10)。XGBoost 相比Gini-RF 而言,对模型的损失函数进行了改进,并加入了模型复杂度的正则项,而LightGBM 是在XGBoost 基础上,优化了模型的训练速度。因此,LightGBM 的泛化能力最好,易发性划区可靠性高。
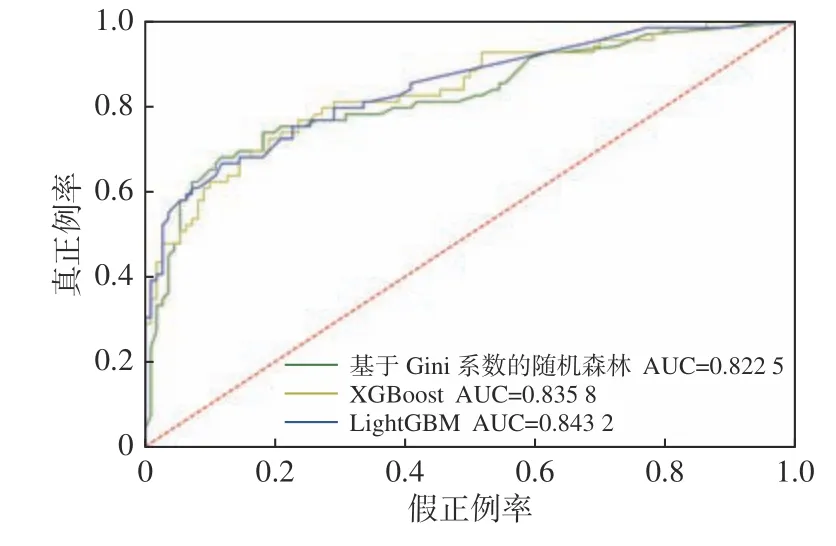
图10 机器学习模型ROC 曲线Fig.10 ROC curve of machine learning model
4.3 典型滑坡验证
对比近几年来雅鲁藏布江与尼洋河两岸发生的滑坡事件(表4),将9 个滑坡信息导入生成的滑坡易发性图中,可知3 个滑坡点位于中易发区,3 个滑坡点位于高易发区,剩余均出现在极高易发区。

表4 近几年以来滑坡事件Tab.4 Landslide events in recent years
为了进一步验证本研究分析方法的可靠性,选择羌纳巴嘎滑坡与墨脱县公路滑坡两处滑坡现场调查进行对比验证(图11)。

图11 典型滑坡验证Fig.11 Verification of typical landslides
西藏自治区林芝地区米林县羌纳乡巴嘎村滑坡位于E 94°24′34″,N 29°20′16″;所处地形地貌为高山河谷地貌;下付基为板岩;斜坡结构为岩土复合斜坡,坡度为30°;植被覆盖率一般,土地利用较低;滑坡前缘至斜坡下方公路,后缘至斜坡山脊处,滑坡体主要为碎土石,滑床为板岩。该滑坡变形特征主要为前方公路开挖斜坡坡脚,导致斜坡失稳。
林芝地区墨脱县公路地处E 93°38′10″,N 29°08′28″,滑坡长为30 m,宽为40 m,厚度为2 m,面积为1 200 m²,体积为2 400 m3,坡度为35°,坡向为260°,滑坡侧边界、前缘清晰可辨。该滑坡微地貌为陡坡,地层岩性为泥岩,位于白龙断层附近,斜坡结构类型为土质斜坡,坡形为凸形,滑坡下方人类活动较少,仅有一小段公路,植被覆盖率较低,为低矮灌丛,滑坡位于河流右凸岸。目前状况为不稳定。
两处滑坡均处于滑坡高易发区,再次验证了本研究机器学习模型划区的准确性。研究结果可供区域滑坡防治相关部门参考。
5 结论
(1)统计各评价因子分级范围内滑坡点数量,表明在高程为32~1 544 m 与2 722~3 752 m、坡度为30°~40°、地层岩性为雅鲁藏布江带闪片岩、土地利用为草地、距断裂带、河流与道路200 m 以内滑坡发生的次数最多。
(2)采用五折交叉验证后,基于贝叶斯优化算法的Gini-RF 模型准确率由原来的0.752 4 提升到0.822 5,XGBoost 与LightGBM 模型准确率也提升了0.032 3与0.017 6。3 种模型对研究区的滑坡分区都具有很高的准确性,其中LightGBM 模型的性能最好,AUC 值、精确度、F1 分数、泛化能力、拟合程度、精确率更高。
(3)利用Gini-RF、XGBoost、LightGBM 等3 种集成机器学习模型对滑坡易发性进行分析,表明滑坡高和极高易发区多位于 墨脱县的达木乡、帮辛乡,林芝县的丹娘、里龙、扎西饶登乡,朗县的陇村,工布江达的江达乡。特别是位于雅鲁藏布江与尼洋河两岸海拔较低、坡度为30°~40°、距河流、道路、断裂带200 m以内的区域。在这些地区应采取相应的地质灾害防治措施。
(4)滑坡极高与高易发性区占比分别为12.14%和12.41%,低和极低易发区分别占26.47%与29.55%,区内一半以上的地区不容易发生滑坡灾害。滑坡易发性分区结果与现场滑坡灾害调查结果吻合较好,同时利用研究区近几年已发生的滑坡点进行验证,表明模型的可靠性高,滑坡分区图可为有关地方部门的防灾减灾活动提供指导。
