镇域尺度下秦巴山区堆积层滑坡易发性不同单元评价性能对比研究

李泽芝，王新刚

（大陆动力学国家重点实验室，西北大学地质学系，陕西 西安 710069）

秦巴山区地质构造强烈，地形起伏大，地貌形态与岩土体结构类型复杂多样，岩体节理裂隙发育，风化严重，降雨丰富，人类工程活动活跃，导致区内灾害频发，尤其是以第四纪堆积层滑坡为主的地质灾害（隐患）具有数量多、分布广、密度大、频次高等特点，所造成的危害严重，是中国地质灾害的重灾区之一（强菲等，2015；赵力行等，2020；刘伟等，2021）。因此，秦巴山区堆积层滑坡具有孕灾条件复杂多样、部分灾害评价数据获取难度大等特征（张世林，2020），如斜坡堆积层厚度、斜坡结构类型。

滑坡易发性评价模型建立流程为：区域滑坡数据及孕灾条件编录→评价因子提取与选择→评价模型选取→模型参数推定→评价结果精度验证与分析等步骤，可见评价模型是十分重要的一环，关乎评价结果的准确性与可信度（黄发明等，2022）。目前滑坡易发性评价模型主要分为知识驱动模型、物理驱动模型、数据驱动模型3 类，其中，数据驱动模型以区域基础环境因子为数据输入，通过机器学习模型、数理统计模型等得到评价结果（Saro Lee et al.，2015；张林梵等，2022）。据研究表明，机器学习模型的预测性能明显高于数理统计模型与传统的知识驱动模型，其中随机森林模型在预测精度、提高泛化能力等方面较其他机器学习模型有着更好的表现，如Merghadi 等（2018）以北非米拉盆地为例，比较了基于随机森林、梯度提升机、逻辑回归、神经网络和支持向量机5种评价模型下滑坡易发性的预测结果，得出随机森林模型预测性能更高的结论。

目前，滑坡易发性评价时所使用区划单元类型主要为栅格单元与斜坡单元（田述军等，2019；常志璐等，2023）。栅格单元区划在空间上破坏了评价区域斜坡的自然属性，但划分时操作简单，在给单元赋值时有更强的唯一性，信息损失较少；斜坡单元划分时相较于栅格更复杂，给单位赋值时可能造成信息损失，但能够很好的反应区域滑坡易发性的地形分布情况，对某些基于斜坡的特征因子有更好的表征，如斜坡结构、堆积层厚度等。

近年来，随着1∶10 000 地质灾害风险评价的开展，评价区域的尺度也转向镇域级，意味着对地质灾害风险区的划分有了相对县域级评价更高的精度要求，主要表现在对全域内每个斜坡孕灾地质条件的掌握（陕西省自然资源厅，2021）。不同地质环境背景下滑坡的主要孕灾因子不尽相同（黄润秋等，2007），如黄土地区由于土体的水敏性、灌溉等因素所致滑坡较为普遍（段钊等，2018），故土地利用类型为黄土地区滑坡易发性评价的重要因子；而秦巴山区多以堆积层碎石土-基岩的二元结构斜坡为主（范立民等，2004；唐睿旋，2017）层间的渗透性差异使该地区以堆积层滑坡为主，故堆积层厚度为堆积层滑坡易发性评价的重要因子。

基于上述分析，笔者选取秦巴山区柞水县小岭镇作为典型研究区，结合堆积层滑坡特点，采取栅格单元、斜坡单元两种单元类型，运用随机森林模型方法对该区域进行了滑坡易发性评价与精度分析，得到镇域滑坡空间概率，并探讨易发性评价在两种划分方法下的差异，研究成果对当地政府部门的减灾防灾措施部署等具有重要意义。

1 研究区及模型特征因子分析

1.1 研究区概况

小岭镇地处秦巴山区腹地（图1），区内地形陡峭、沟壑纵横，其地质构造受东西展布的山阳—凤镇等深大断裂影响较大，其滑坡孕灾条件也较为复杂：区域内斜坡以二元结构的陡坡为主，丰富的矿产资源与稀少的平缓地带，不可避免的形成了区内削坡建房频繁、切坡修路密集、毁林造地普遍、矿山开发持续的现象，这些现象导致了斜坡开挖形成临空面致使开挖处剪应力集中，加之堆积层大都为渗透性强的松散碎石土，矿区附近更有矿渣堆积使得堆积层自重增大，孔隙水压力增强，导致堆积层滑坡在研究区内极易发育，经统计发现（表1），研究区地质灾害以堆积层滑坡为主，占区内滑坡的92.86%，主要分布在道路两侧的陡坡处（图2）。

表1 研究区滑坡规模分类Tab.1 Classification of landslide scale in study area

图1 研究区位置图Fig.1 Location of the study area

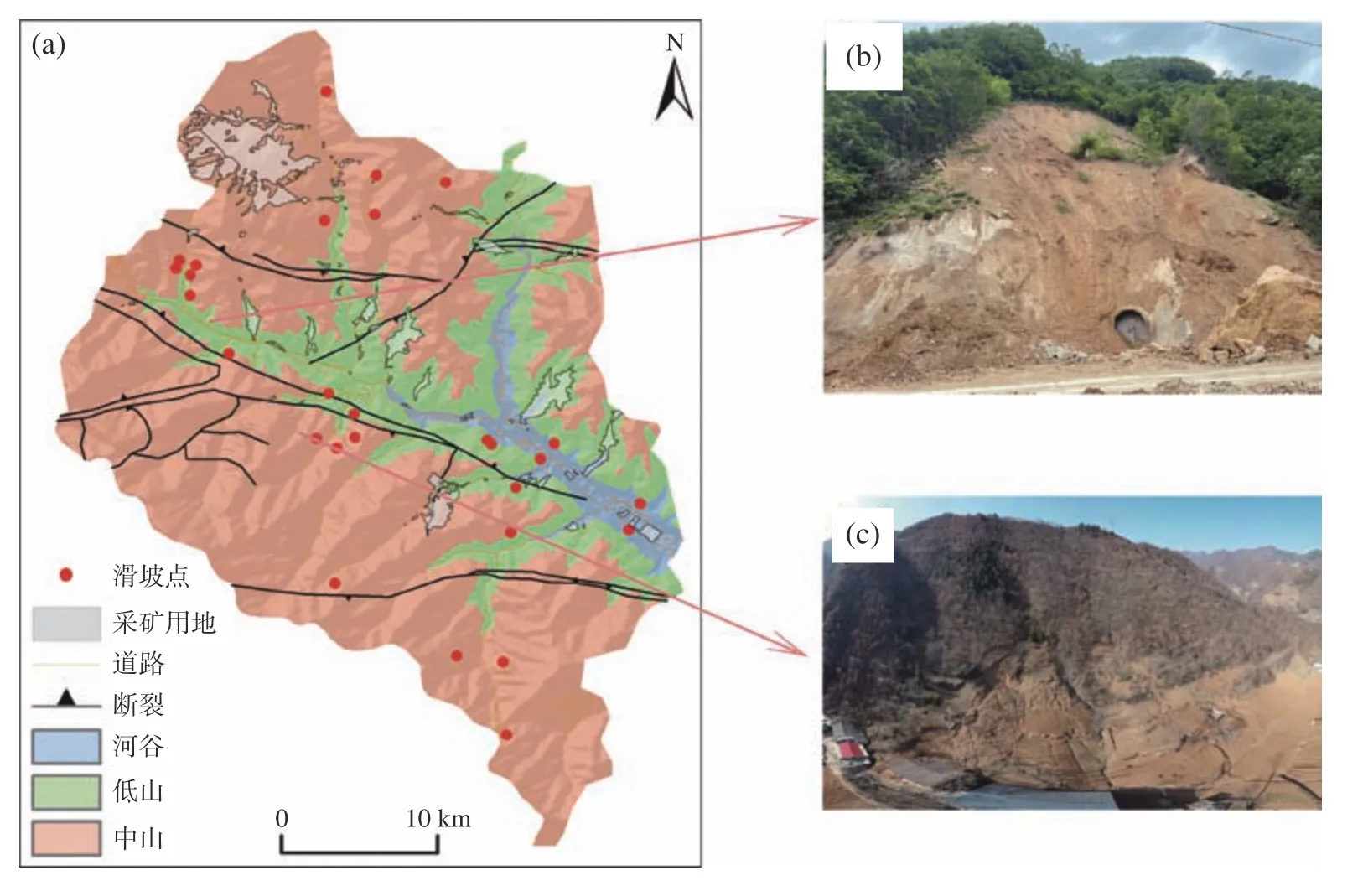
图2 研究区已有堆积层滑坡分布图Fig.2 The distribution of alluvial landslide in the study area

1.2 随机森林模型简介

随机森林是一种集成Bagging 算法，可用于分类问题与回归问题（方匡南等，2011）。在分类问题中，旨在生成众多决策树，并通过对建模数据集的样本观测和特征变量分别进行随机抽样，每次抽样结果均为一棵树，且每棵树都会生成符合自身属性的规则和分类结果，而森林最终集成所有决策树的规则和分类结果，实现随机森林算法的分类。其主要特点在于数据采样随机、特征选取随机。

2 模型数据制备

2.1 数据来源及用途

将镇域孕灾因子数据赋予评价单元作为随机森林分类模型的样本数据，其中孕灾因子为模型特征因子，区域滑坡环境特征因子数据源主要包括遥感影像数据、表面数字高程模型、地质图、野外调查数据等，其分类及用途见表2。

表2 数据类型及用途Tab.2 Data types and uses

2.2 评价单元

①栅格单元：研究区栅格共计4 576 590 个栅格；提取出滑坡周界内所占栅格，共计6 192 个栅格单元（图3）。

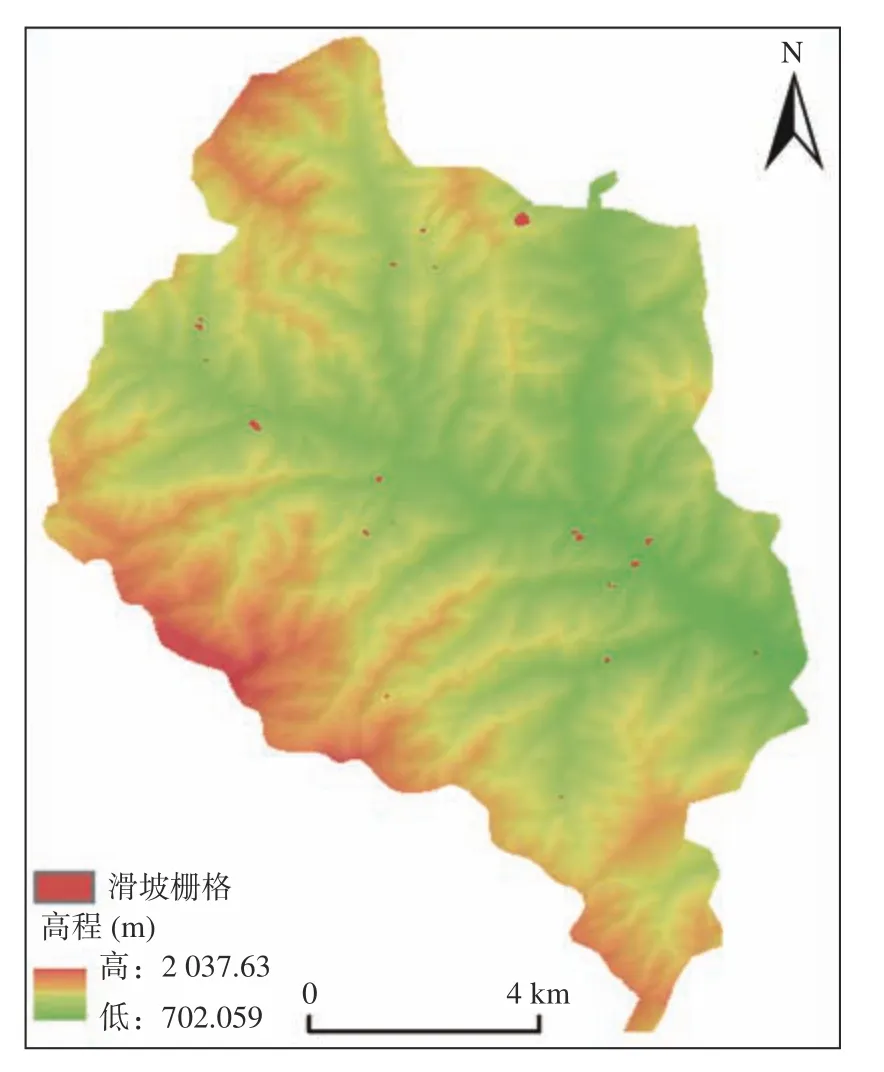
图3 研究区栅格单元划分Fig.3 Grid division of Study Area

②斜坡单元：对研究区DEM 用水文分析模型进行斜坡单元初步划分，再结合研究区卫星影像图与10 m 等高线进行人工校正（谷天峰等，2013；刘彬等，2021），最终将研究区划分为729 个斜坡单元（图4），单个面积概况见表3，对其中滑坡所在斜坡单元进行标记，共计28 个斜坡单元。

表3 斜坡单元面积概况Tab.3 Overview of slope unit area

图4 研究区斜坡单元划分Fig.4 Slope division of study area

2.3 特征因子

滑坡的发生是一个由多种因素作用下产生的非常复杂的非线性过程，要通过机器学习模型对全区发生滑坡的概率进行分级，特征因子的选取至关重要（Ahmed et al.，2016；吴润泽等，2021），当根据研究区滑坡的孕灾特点，有针对性的选取。在前人研究基础上，结合区域孕灾特征，初步选9 个孕灾因子作为模型特征因子用于建模，并依据特征属性，将特征因子进行离散化后做出属性空间划分（图5），具体如下：

图5 研究区滑坡地质灾害易发性评价指标因子Fig.5 Index factors of landslide geological hazard Susceptibility assessment in the study area

①地形因子：坡度、坡高。

滑坡的主要动力来源于自重，坡度则控制着斜坡内部的应力分布，是滑坡的重要影响因素。将研究区斜坡坡度划分为：0～15°、15°～25°、25°～35°、35°～45°和＞45°等5 个属性空间。

在岩土类型大致相似的地质环境下，坡体高度影响着坡体自重大小以及斜坡范围内地形变化，进而影响滑坡的规模与范围（郭芳芳等，2008）。先将DEM重采样为5 m×5 m 栅格，再利用分区统计工具得到坡体高度范围，将其分为0～20 m、20～50 m、50～100 m、100～300 m、＞300 m 等5 个属性空间。

②斜坡自身特征：斜坡坡面形态、斜坡结构、斜坡堆积层厚度。

斜坡形态以其剖面曲率划分，剖面曲率定义为曲面在最陡斜坡方向上的曲率，当曲率值＜-0.5 时值判断为凹型坡，曲率值＞0.5 时判断为凸型坡，曲率值在-0.5～0.5 之间时判断为直线型坡。

据前人研究，斜坡结构在堆积层滑坡的发生中也是一个重要的影响因素（邢林啸等，2012；贾琳等，2021），从研究区已发生的堆积层滑坡来看，39.13%都发生在顺向斜坡中，而逆向斜坡中无已发生滑坡，故根据野外调查数据，将区内斜坡结构划分为：顺向斜坡、斜向斜坡、横向斜坡、近水平状斜坡、切向斜坡、逆向斜坡等6 个属性空间。

由于区内滑坡大都为堆积层滑坡，堆积层厚度在一定程度上决定了土地利用类型、边坡开挖程度、地下水位埋深，对堆积层滑坡起着重要启发作用，但对于这一指标，目前缺乏经济又精准的测取方法，本研究方法如下：对每个坡体随机抽点使用插杆进行测量得到平均数，结合依托项目的工程钻探数据对调查结果进行修正并类比到全区，赋值给每个斜坡，将该因子划分为：0～1 m、1～3 m、3～6 m、6～10 m、＞10 m等5 个属性空间。

③人类工程相关特征：距道路距离、距河流距离、距矿区距离。

区内平缓地带稀少，道路开通处往往伴随着边坡开挖，形成陡立临空面；河流对坡脚的侵蚀、依河而居带来的切坡建房；矿山的开挖、震爆、不合理的矿渣堆积，这些因素都为滑坡的发生提供了有利条件。距河流、道路、矿区的距离均可反应人类工程活动的强弱程度，其各自属性区间划分如图5 所示。

④地质条件：距断裂距离。

区内受山阳—凤镇等深大断裂影响较大，该断裂呈近东西展布，经凤镇横贯研究区，该断裂对区内表层岩体破坏严重，加之研究区内节理裂隙极为发育，极大地破坏了岩土体的完整性，增加了滑坡的发生概率。对研究区地质图进行矢量化，提取研究区内断裂为矢量文件，对其做缓冲分析，划分为0～100 m、100～400 m、400～700 m、700～1000 m、＞1000 m 等5 个属性区。将上述特征因子赋值给两种划分单元：①栅格单元：在Arcgis10.7 中，将栅格转化为点数据，用“多值提取至点”工具将各因子值提取至点，与初步选取的9 个因子构成矩阵A4576590×9，作为原始样本1。②斜坡单元：除斜坡结构等因子在每个斜坡单元有唯一值外，对于坡面形态等离散型变量，取其众数赋值；对于坡度等连续型变量，取其平均数赋值，729 个斜坡单元与初步选取的9 个因子构成矩阵B729×9，作为原始样本2。

对两种划分单元下的原始样本分别进行频率比分析，得到各因子属性区间的频率比值。频率比值的大小可反应该属性空间滑坡发育的优势程度（郭子正等，2019），若某属性空间评价单元样本数过少（如斜坡单元中近水平斜坡数量），则在选择优势空间时，剔除该属性空间，最终统计得各因子的滑坡发育优势空间（表4）。

表4 两种评价单元下各因子的滑坡发育优势空间Tab.4 Dominant space of landslide development of each factor under two evaluation units

随机森林模型对特征因子的相关性有一定要求，因子之间相关性过高会降低模型的训练精度。对研究区特征因子首先进行正态性检验，以确定相关性分析的计算方式。若数据满足正态分布，则选用Pearson相关性分析；若数据不满足正态分布，则用Speraman相关性分析；针对有序变量数据，则选用Kendall’staub 等级进行相关性分析。

由表5 可知，两种评价单元下各因子显著性P 值均为0.000***，水平呈现显著性，拒绝原假设，因此数据不满足正态分布。由于数据为有序数据，选用Kendall’s tau-b 等级进行相关性分析（表6、表7）。由结果可知，栅格单元下，研究区距河流距离与距道路距离特征因子的相关性系数为0.653＞0.3；斜坡单元下，研究区距河流距离与距道路距离特征因子的相关性系数为0.606＞0.3，说明两种评价单元下道路与河流之间的相关性都较高。由于研究区堆积层滑坡主要分布在道路两侧，故剔除河流距离因子，最终采用其他剩余8 个因子进行建模评价。

表5 特征因子数据正态性检验结果Tab.5 Characteristic factor data Normality test results

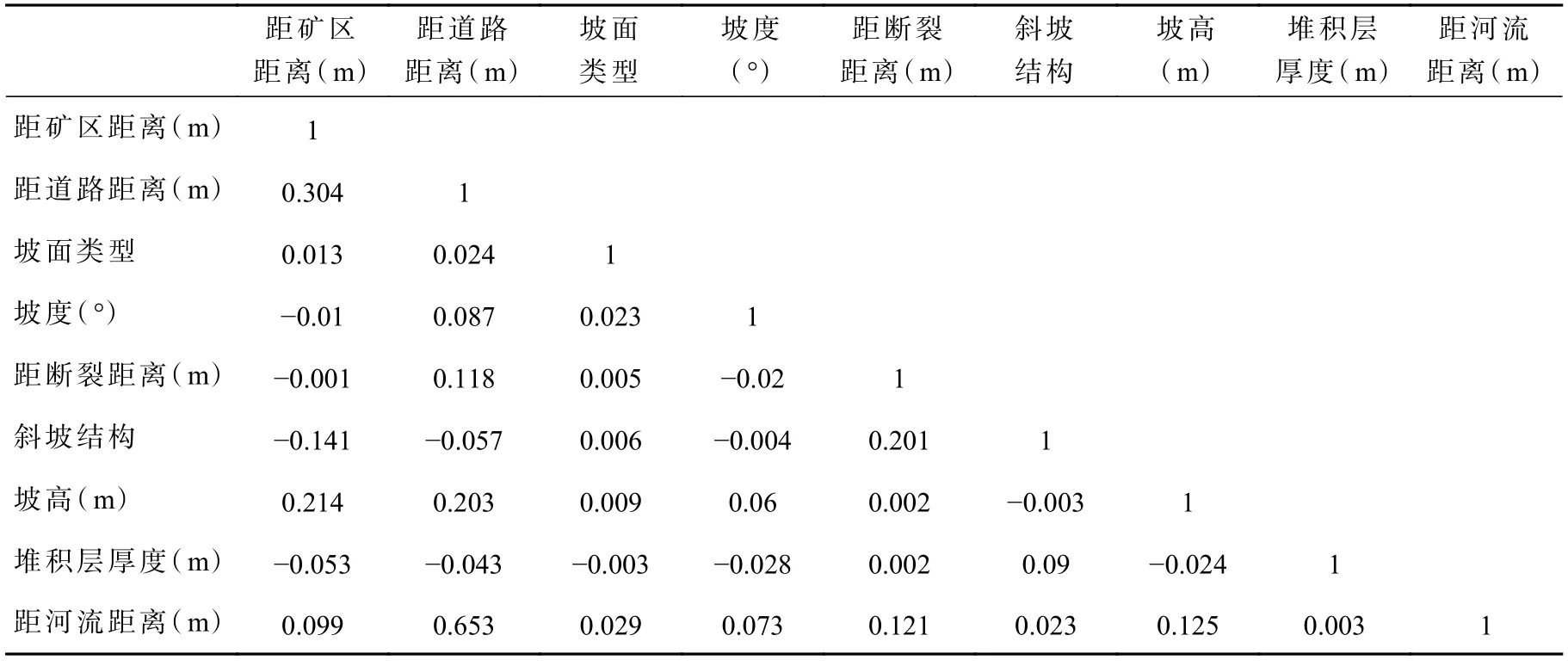
表6 特征因子Kendall’s tau-b 等级相关系数矩阵（栅格单元）Tab.6 Characteristic factor Kendall’s tau-b rank correlation coefficient matrix (grid units)

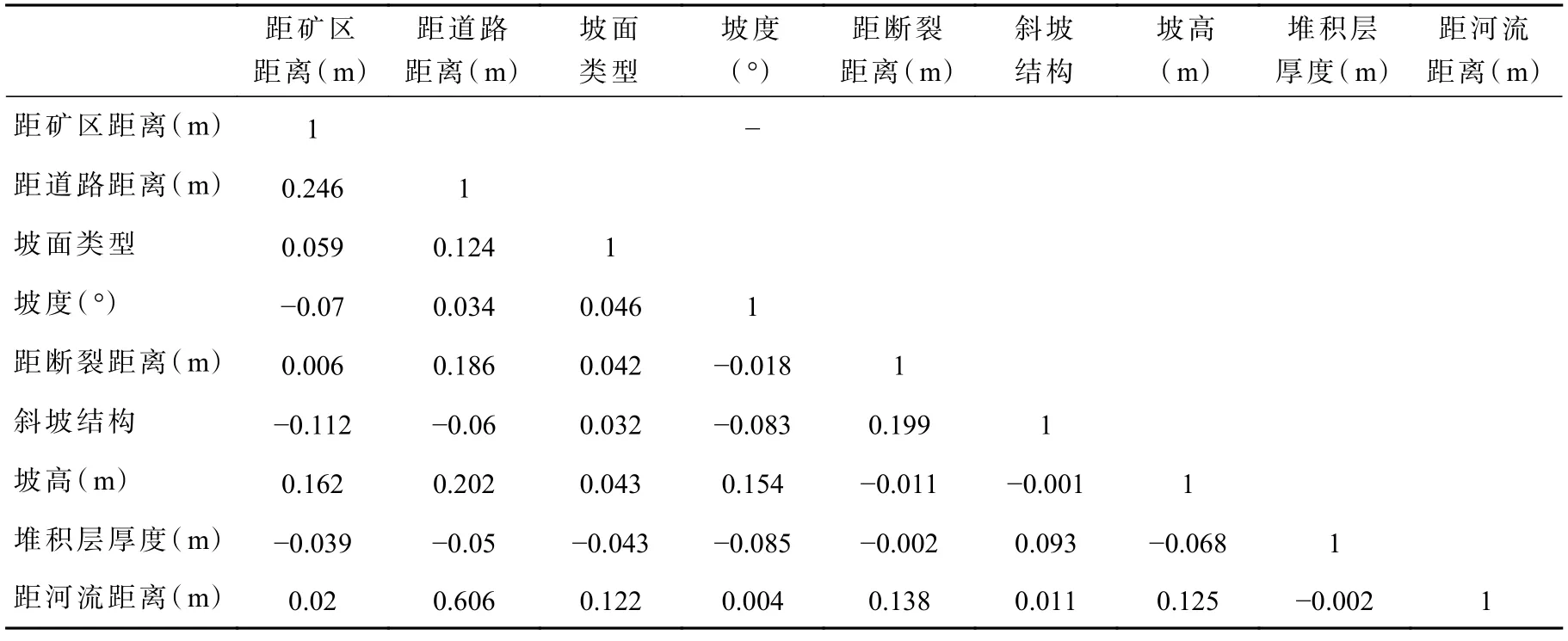
表7 特征因子Kendall's tau-b 等级相关系数矩阵（斜坡单元）Tab.7 Characteristic factor Kendall's tau-brank correlation coefficient matrix (slope units)

3 评价及结果对比分析

3.1 评价结果

对于栅格单元，将4 576 590 个栅格单元转化为连接有各因子数据的点后，将6 192 个滑坡栅格点作为滑坡样本并将其易发性赋值为1，占总样本的0.13%，在滑坡范围外选取3 倍于滑坡样本的点作为非滑坡样本，以减少滑坡与非滑坡样本之间的数量不平衡与空间相关性，并将其易发性赋值为0，两类数据合并后以7∶3 的比例划分为训练集与测试集，在R 语言的RF 软件包中构建随机森林模型，将合并后数据输入进行训练。训练结束后，将整个研究区点数据输入，得到所有点的易发性值。将点数据转为栅格，利用自然间断法划分出极低、低、中、高、极高等5 个易发区（图6）。对于斜坡单元，选取28 个滑坡所在的斜坡单元作为滑坡样本并将其易发性赋值为1，占总样本的3.8%，在滑坡范围外选取3 倍于滑坡样本的点作为非滑坡样本，并将其易发性赋值为0。剩余操作与栅格单元类似，结果见图6。由图6、表8 可知：①两种评价单元下滑坡易发性分区大体相近，滑坡高、极高易发区主要位于镇域北部矿区附近、西北部道路切坡密集区域、西南部盘山公路切坡密集道路附近，表明研究区内滑坡的发育与道路、矿区的影响有较强的相关性，这也与实际情况相符合。②栅格单元下预测的极低、低、中、高和极高易发区占研究区全区比例为：66.76%、19.50%、8.99%、3.04%和1.71%，已知滑坡样本在高、极高易发样本量中占95.49%；斜坡单元下预测的极低、低、中、高、极高易发区占研究区全区比例分别为61.92%、17.70%、10.09%、5.25% 和5.04%，已知滑坡样本在高、极高易发样本量中占96.42%。③栅格单元下高、极高易发区频率比之和占总频率比值为0.93，略低于斜坡单元下比值0.98，可知斜坡单元下的滑坡易发性可更好的判断已知滑坡，且斜坡单元下的评价可很好的表现滑坡的地形分布特点。

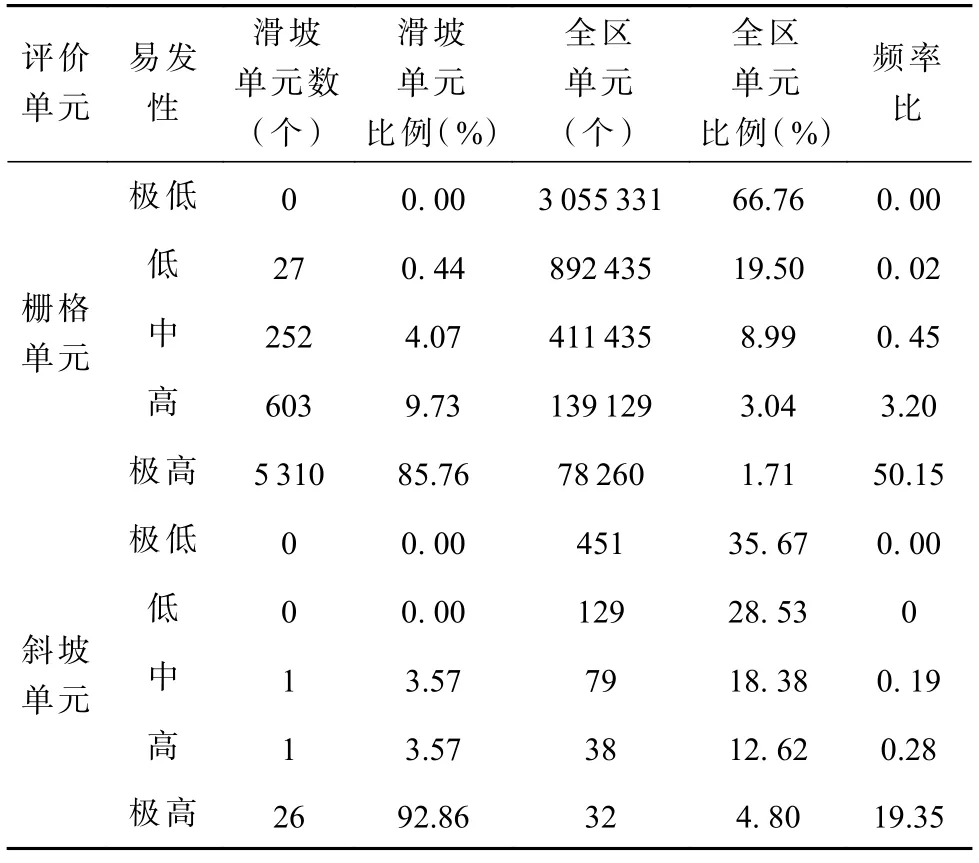
表8 栅格单元与斜坡单元下评价结果频率比Tab.8 Frequency ratio of evaluation results under grid unit and slope unit

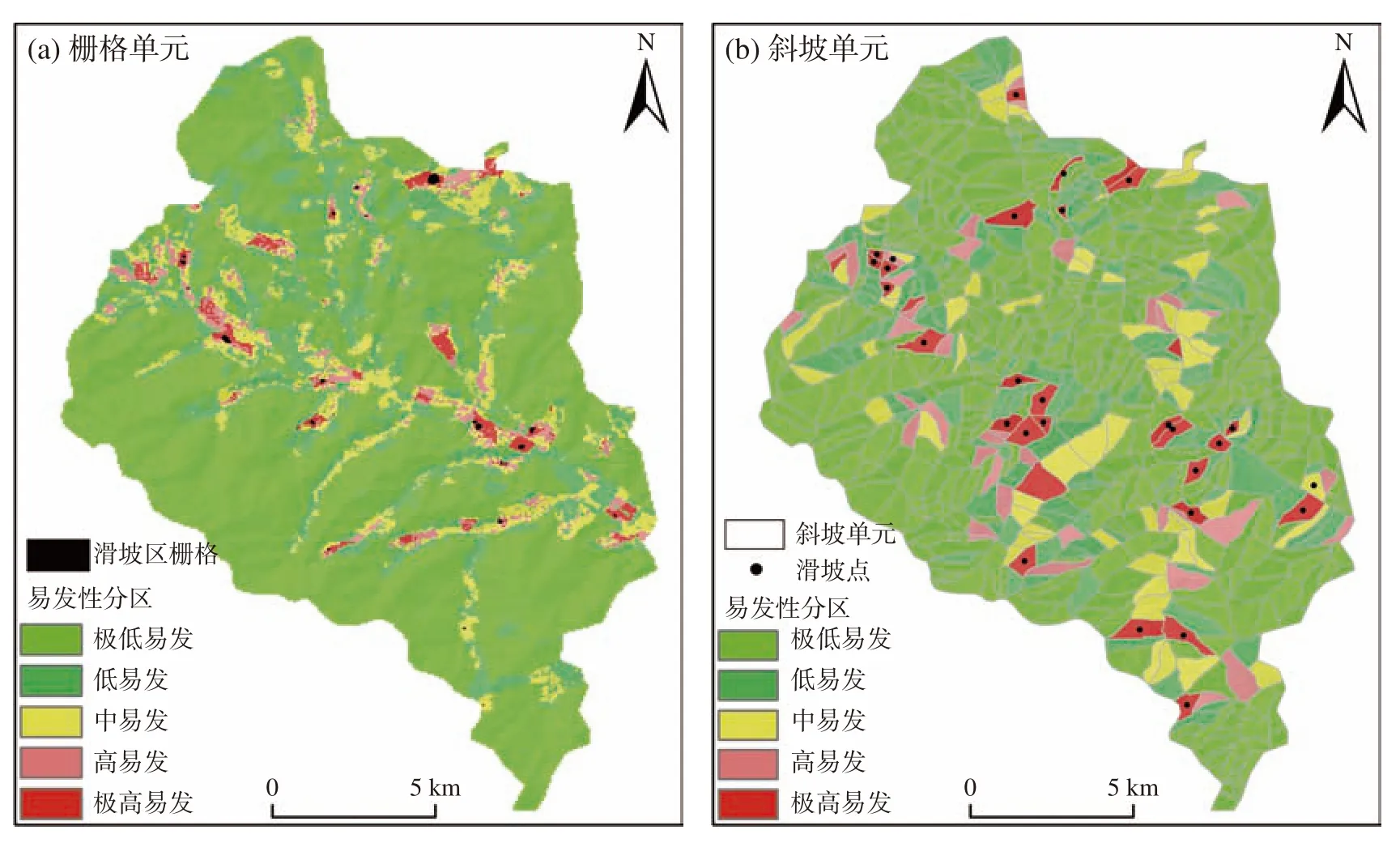
图6 研究区滑坡易发性区划Fig.6 The division of landslide susceptibility in the study area

由模型得到两种评价单元下各特征因子的重要性比例（图7），可知道路开挖、斜坡结构对滑坡的发生起主要作用，事实上，现有滑坡多发生在道路两旁及顺向结构斜坡中。

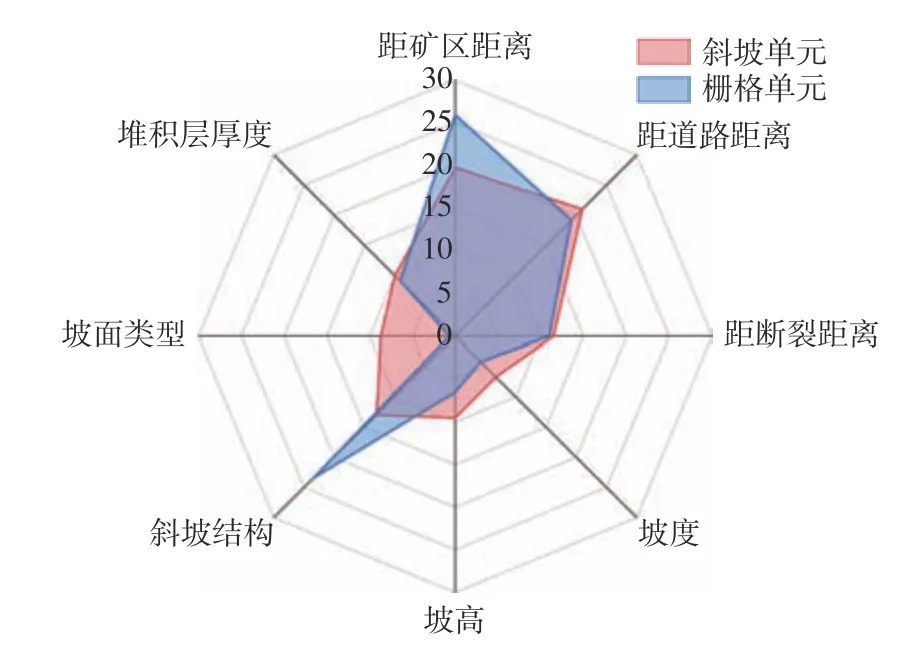
图7 各特征因子贡献值Fig.7 Contribution value of each characteristic factor

3.2 模型精度及评价结果对比

结合前人研究（刘坚等，2018；郑迎凯等，2020），笔者选取ROC 曲线来进行模型精度验证。将全部样本滑坡易发性概率递减排序，阈值从1 至0 变更，计算各阈值下对应的（FPR、TPR）数值对，将数值对绘制于直角坐标系中。横坐标FPR 代表非滑坡预测为滑坡的数量/真实非滑坡数量；纵坐标TPR 代表滑坡预测为滑坡的数量/真实滑坡数量。曲线下面积（AUC）越接近1，则说明模型预测性能越高。根据两种评价单元下预测结果，绘制各自ROC 曲线（图8），可以看出，基于栅格单元、斜坡单元下随机森林模型的AUC值分别为0.864、0.921。表明5 m 高精度栅格单元下随机森林模型的预测精度小于基于斜坡单元下模型的预测精度。

图8 ROC 曲线Fig.8 ROC curve

滑坡的发生相对于整个区域是一个小概率事件，整个区域内滑坡易发性概率在预测模型精度较高的情况下，均值越低，表明预测的不确定性越低；标准差越低，表明预测区分度更优，由表9 可知，栅格单元下预测滑坡易发性概率均值为0.10 小于斜坡单元下滑坡易发性概率均值0.13；栅格单元下预测滑坡易发性概率标准差为0.13，小于坡单元下滑坡易发性概率标准差0.18。说明栅格单元作为评价单元，预测结果具有较差的区分度，斜坡单元反之。

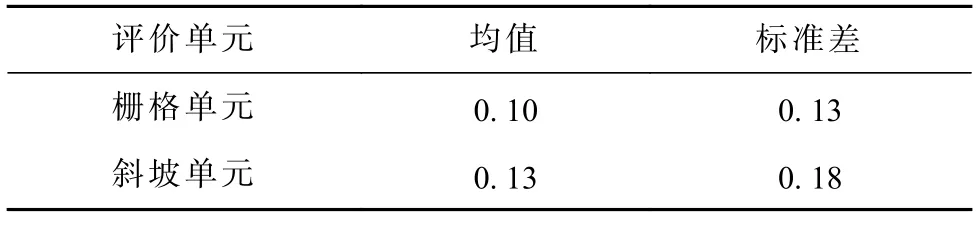
表9 不同评价单元下易发性概率均值与标准差Tab.9 Mean and standard deviation of probability of Susceptibility under different evaluation units

4 结论

（1）结合研究区孕灾特征，选取了坡度、坡高、坡面形态、斜坡结构类型、堆积层厚度、道路、矿区、区域地质断裂等8 个孕灾因子作为模型特征因子，栅格单元、斜坡单元两种评价单元的预测结果，均发现模型主要根据道路、斜坡结构等因素区分滑坡、非滑坡区域。据各因子频率比值可知，研究区内，在距道路100 m 内的顺向浅层堆积层斜坡中，最易发生滑坡。

（2）在栅格单元、斜坡单元两种评价单元下，研究区95.49%、96.42% 的滑坡落在随机森林模型预测分区出的高、极高易发区内；通过AUC 值、易发性概率均值、易发性概率标准差对比表明：随机森林是一种可靠、全面的滑坡易发性预测模型，评价单元为斜坡单元时预测精度更高、准确性更强。

（3）滑坡易发性评价中，栅格单元与斜坡单元在评价结果上，两种评价单元的预测结果都有良好的表现。栅格单元的样本数远高于斜坡单元，意味着样本数据中滑坡样本比例减小，样本的不均衡性增大，使得随机森林模型的预测结果性能变弱，但以栅格单元为评价单元可减少特征因子的数据损失，在灾害防治具体空间部署上有着更精细的参考；斜坡单元在特征因子赋值时，会造成部分数据损失，但其能更好体现滑坡灾害的地形空间属性，相较于栅格单元其样本的不均衡性更小，使得其基于随机森林模型的预测性能高于栅格单元。