自动泊车系统规划与控制方法研究

孙柯阳,王兆强,梁威,刘斌山,孙崇智

（1.上海工程技术大学机械与汽车工程学院,上海 201620；2.甘肃省特种设备检验检测研究院,甘肃 兰州 730050）

由于民用汽车拥有量的增长,在有限的生活空间内,司机在泊车过程中容易产生泊车事故,自动泊车系统是解决此类问题的一种有效方法[1],通过传感器与控制算法技术的融合,自动泊车系统可以提升城市空间的利用效率,降低事故发生率及保障行人安全.

自动泊车系统主要有环境感知、决策规划及控制执行[2-3]三大关键技术.现已有许多与自动泊车系统相关的研究,如：Vorobieva 等[4]分别基于单个和多个圆弧规划不同的泊车路径,且根据回旋线进行平滑处理,然而此方法规划的泊车路径起点与终点处的曲率不为零,会造成车辆原地转向；Zips 等[5]将运动学微分方程离散化制定静态优化问题,通过迭代求解,缩短了泊车路径,但此方法由于忽略了路径曲率的连续性,因此泊车过程车辆行驶不平顺；钱立军等[6]基于最短泊车时间,提出最优控制问题,且使用高斯伪谱法提升了求解效率,然而此方法缺乏对控制器的研究,因此跟踪精度低.针对上述研究中泊车路径曲率不连续与缺乏控制器跟踪控制的问题,本文重点对泊车的路径规划、车辆跟踪控制及控制器的优化进行研究.

1 动力学模型建立

车辆是由车身、底盘及发动机组成的复杂的非线性系统,需要繁杂的非线性微分方程来表示车辆数学模型,然而此方法会增加系统的计算量及降低实时性,因此本文在简化车辆模型的基础上,结合阿克曼转向几何建立了车辆动力学模型,如图1 所示.

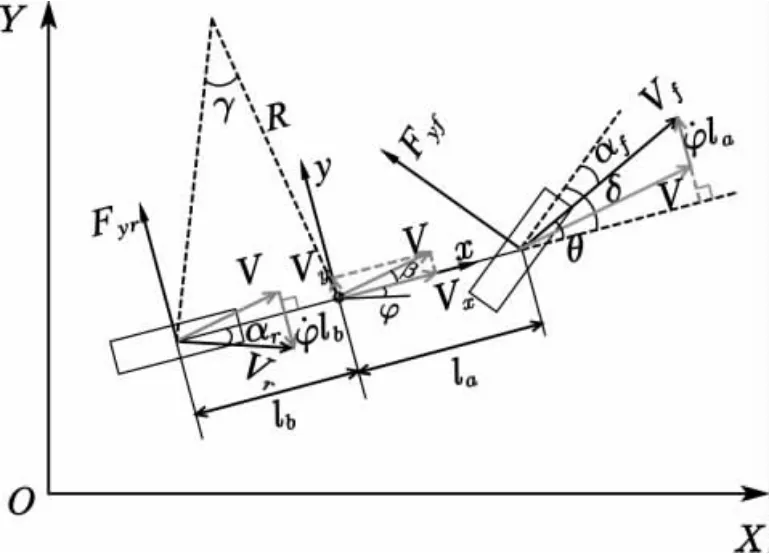
图1 车辆动力学模型Fig.1 Vehicle dynamics model

图1 中,R为质心处转弯半径,Vf、Vr、V分别为前后轮速度及质心速度,la和lb分别是前后轴到质心处的距离,αf、αr、β、δ、φ、θ 分别是前轮侧偏角、后轮侧偏角、质心侧偏角、前轮等效转角、横摆角及航向角、Fyf和Fyr分别为前后轮所受侧偏力.对图中车辆模型进行受力分析可得

式（1）中：m是整车质量,I为转动惯量.当轮胎侧偏角很小时,轮胎侧偏力与侧偏角呈线性关系,可表示为Fy=Cα,其中C是侧偏刚度,因此前轮等效转角较小时,根据式（1）可得

对图中速度关系进行分析可得

由于车辆行驶过程中,轮胎侧偏角较小,因此可以求得前后轮侧角αf与αr的大小

根据公式（2）（3）和（4）,可以得到关于Vy和的状态方程

2 泊车路径规划

2.1 B-spline 曲线

B-spline 曲线具有易于控制、节点间连接平滑且可以进行局部修改曲线形状的优点,因此本文采用B-spline 曲线用以规划泊车曲线,n次B-spline 曲线的公式见式（6）

式（6）中：u∈[0,1]；n为样条曲线的阶数；Pi表示第i个控制点；Bi,n（u）表示第i个n次基函数,如式（7）所示

由于三阶B-spline 曲线的二阶导数连续,满足泊车过程中,参考曲线曲率连续的要求,因此,公式（6）与公式（7）中n=3,可求得三阶B-spline 曲线的表达式,如式（8）

其中P1、P2、P3与P4为曲线的控制点,根据公式（8）即可得出参考路径的斜率与曲率公式,如式（9）（10）

2.2 曲线控制点的计算

在计算控制点的过程中考虑碰撞约束且采用逆向泊车法对操作过程进行研究,具体过程如图2所示.

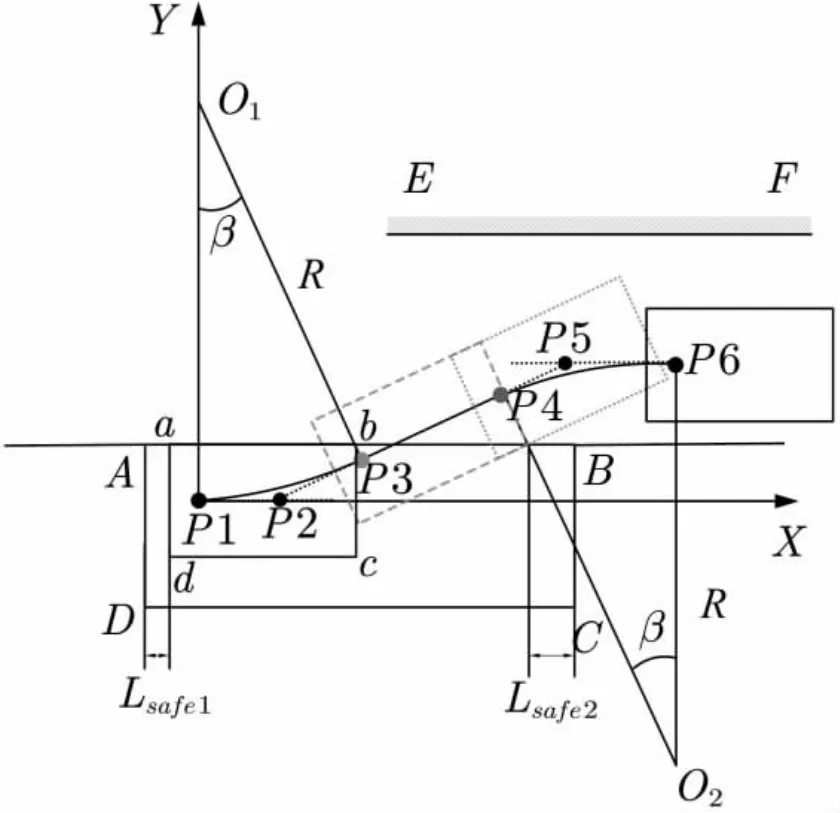
图2 逆向泊车过程Fig.2 Reverse parking process

车辆从车位驶出总共分为三个阶段：P1P3、P3P4 与P4P6.在P1P3 段,车辆行驶至虚线位置时,车辆外轮廓点c与车位拐点B有一定的安全距离Lsafe2=Lsafe1=200 mm,此时车身转动β 度,可求得

根据β 的数值可以求得P1 与P3 之间坐标差值ΔP13 为

为避免右侧车身与拐点B发生碰撞,需要回正方向盘,使车辆沿直线行驶至图中点线位置,根据图中关系可求得P3 与P4 之间坐标差值ΔP34 为

在P4P6 阶段,可以求得P5 与P6 之间坐标差值ΔP56 为

由于参考曲线的曲率不能过大,因此取P3P4 的延长线与P1 点切线的交点为P2 点,同理可得P5点,P2 与P3 之间坐标差值ΔP23 为

P4 和P5 点之间的坐标差值ΔP45=ΔP23,因此确定P1 点坐标即可确定各个控制点的坐标.设P1=（x,y）,则各控制点的坐标计算如下

3 基于LQR 与FLA 的控制器的设计与优化

3.1 基于LQR 的控制器设计

自动驾驶车辆在行驶过程中,由于外部环境与自身因素的影响,车辆实际运动路径与参考路径之间存在一定的误差,见图3.

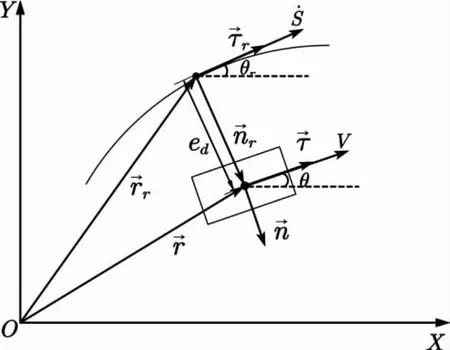
图3 横向误差示意Fig.3 Schematic diagram of lateral error

令φ=eφ+θr,根据公式（17）可以得到以下公式

实际道路曲率变化较为平缓,因此可以忽略的计算,将公式（18）带入公式（5）可得

公式（19）可以简化为

分析公式（20）可知,控制器的目标为选取合适的控制输入u,使得实际路径与规划路径之间的误差e尽量小,因此可以将此类问题转化为求解线性二次型调节器（linear quadratic regulator,LQR）问题[7],即

式（21）中：X为误差量err,Q=[q1,q2,q3,q4]和R=[r]分别为误差与输入对应的权重矩阵,由于参考路径是由大量离散化的参考点所组成,需要将=AX+Bu离散化为Xk+1=AXk+Buk,然后进行求解代价函数的极小值,因此可得如下公式

式（22）中：ξ∈[t,t+dt],进一步利用欧拉法处理公式（22）并化简可得

基于拉格朗日乘数法构造如式（24）所示函数,即可求得代价函数的极值

为了简化式（24）,可构造Hamilton 方程[8],令可得

通过求解上述公式,最终可以得到一个Riccati 方程

进一步可求得控制量uk的表达式

式（27）可以简写为u=-KX,其中,系数和R已知.

分析公式（20）可知,K取任意值时,系统无法同时消除误差及其变化量,因此,引入一个控制量δf,有,当e˙rr=0时,,因此可以选择合适的控制量δf使得err=0,式err为

式（28）中：系数K1和K3由LQR 求出,当横向误差ed=0 时,对于横摆角误差eφ,根据图1 进行分析,由于质心处转弯半径R远大于后轴到质心的距离lb,因此,有eφ=-γ-αr,根据包含γ 角的虚线三角形的角度关系有β=γ+αr=-eφ,带入eφ=φ-θr,可得θ=θr,车辆的航向角误差总是为零.

3.2 基于FLA 的控制器优化

通过对LQR 控制器的设计过程进行研究,分析得出影响泊车系统性能的因素主要有泊车行驶速度及控制器的权重矩阵Q=[q1,q2,q3,q4]和R=[r],具体影响效果如图4、图5 所示.

图4 不同速度下状态矩阵Fig.4 State matrix at different speeds

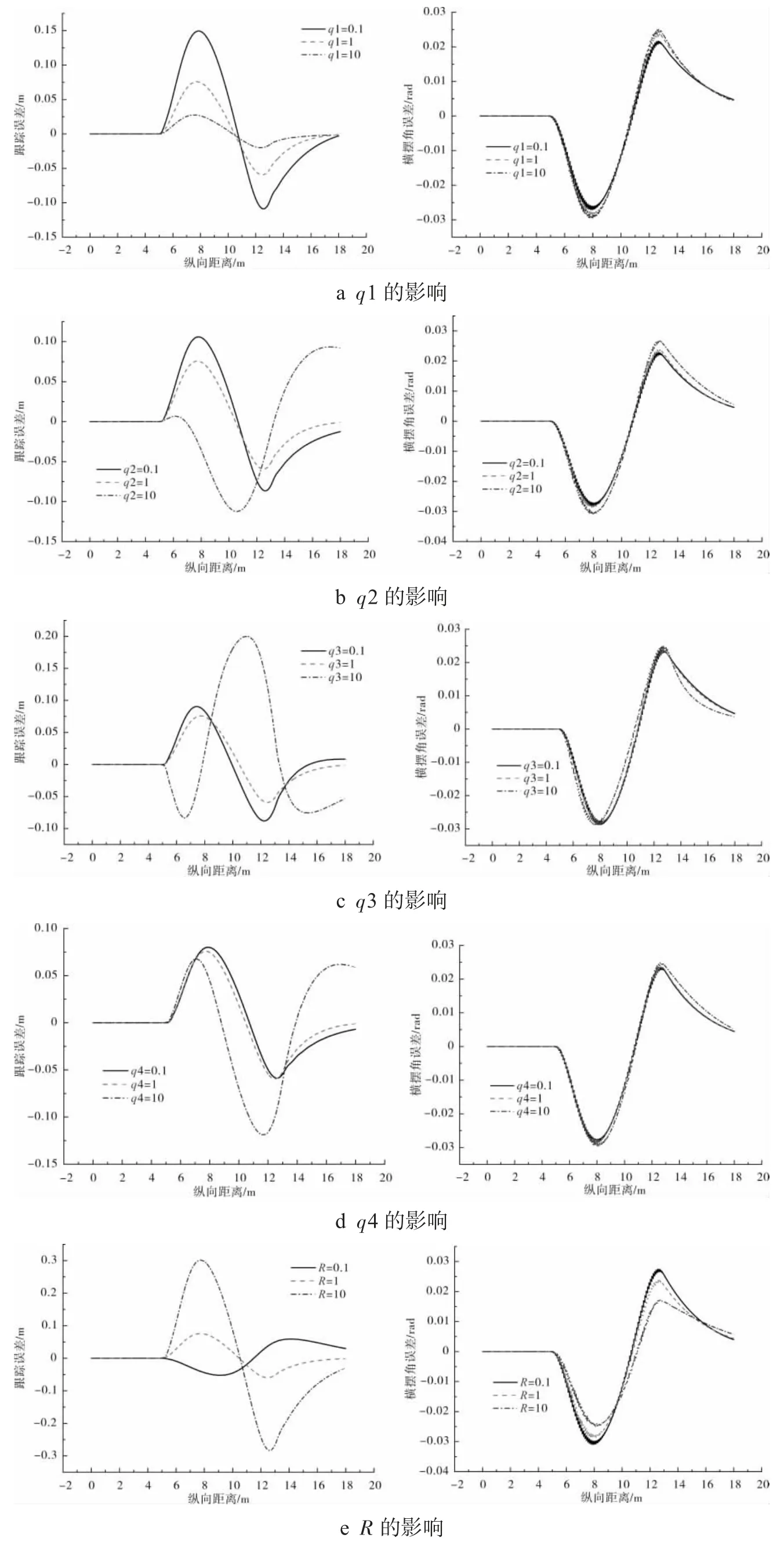
图5 不同系数下控制效果Fig.5 Control effects under different coefficient

图4 为不同速度下状态矩阵A的变化,对比图4-a、b、c 和d 可以得出随着速度的增大,状态矩阵中的部分系数随之减小,因此,在不同速度场景下泊车精度不同.图5 为不同权重系数条件下车辆跟踪五次多项式S 型曲线,车辆的跟踪误差与横摆角误差,对比图5-a、b、c 和d 可以发现q1 与q4 作用下的控制器稳定且跟踪误差与横摆角误差较小,相反的,q2 与q3 对控制器的精度影响较小且会降低控制器的稳定性.对于权重系数R,当R=0.1 与R=10 时,控制器的跟踪效果不佳,因此直接取R=1,即有较好的控制效果.

现阶段可以通过不断试验调整权重矩阵以达到良好的跟踪效果,然而此方法人工成本较高,随着计算机技术的发展,有各类优化算法被广泛地应用于权重系数的选取,如灰狼算法[9]、蓝鲸算法[10]与神经网络[11],而智能控制算法中的模糊逻辑算法（Fuzzy Logic Algorithm,FLA）是基于人的经验进行设计的,因此,对于精度低,非线性与时变性的被控对象也有很好的控制效果,可通过模糊逻辑算法代替人工进行参数调整.模糊逻辑算法的设计过程主要有三步：模糊化、模糊推理与解模糊[12].以误差e为输入,控制因子r为输出,最终通过q=10r计算得出最终的权重系数.首先,确定模糊词汇为：负大（NB）、负小（NS）、零（ZO）,正小（PS）和正大（PB）,定义输入量的论域为[-0.6,0.6],输出量的论域分别为[-1,1]和[-1,0.5],得到隶属度函数,见图6.

图6 各隶属度函数Fig.6 Membership functions

为了后续的模糊推理,需要制定相应的模糊规则库,研究图5 中各系数作用下的控制规律可得到规则库,见表1 和表2.

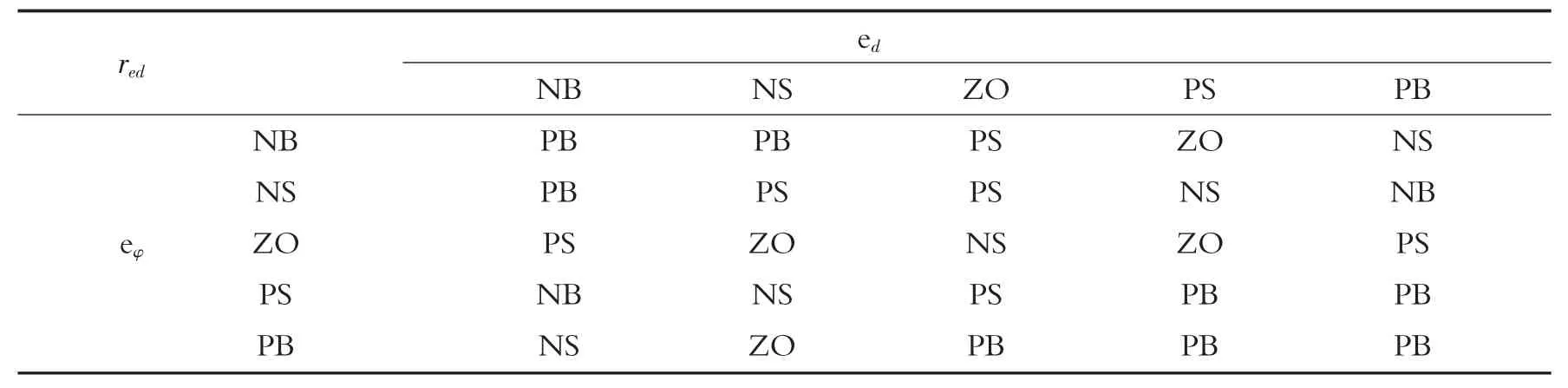
表1 red 的规则库Tab.1 The rule base of red

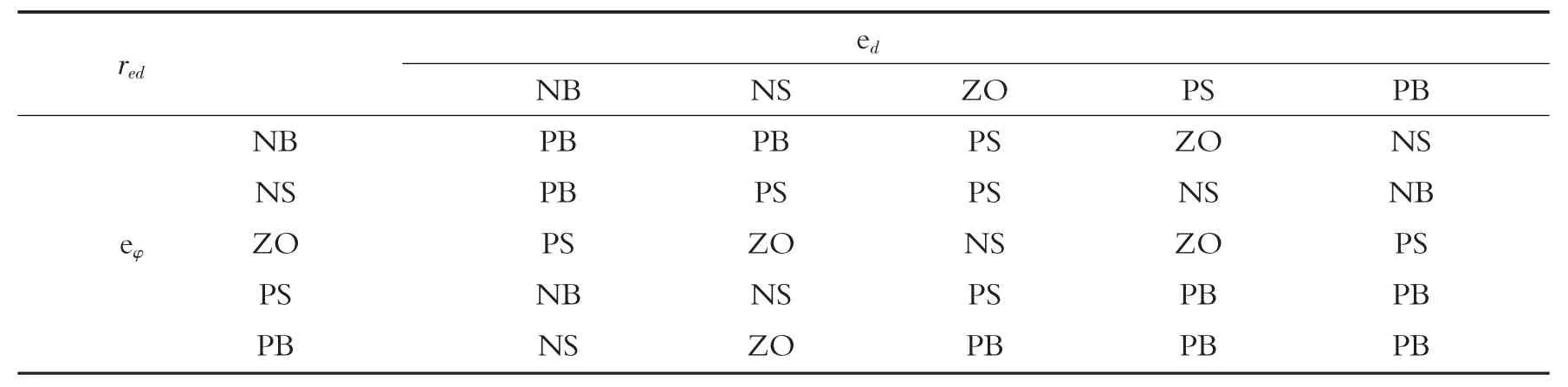
表2 reφ的规则库Tab.2 The rule base of reφ

由模糊推理得到的值为模糊值,需要相应的解模糊方法将模糊值转化为实际值,本文使用加权平均法进行处理,得到控制器所需的实际值如图7 所示.

图7 输出精确值Fig.7 The exact value of output

3.3 基于Frobenius 范数的更新方法

由于实际泊车场景的复杂性,泊车过程中车辆在不同场景下行驶速度不同,且模糊逻辑算法计算过程是实时的,需要相应的更新方法以降低计算量,提升对不同速度的泊车场景的适应度,因此,本文将基于Frobenius 范数的相似度计算引入优化过程中,通过对比范数的接近程度,可以确定两个矩阵之间的差异.

以状态矩阵A为例,矩阵A为当前速度下的状态矩阵,A1 为另一速度下的状态矩阵,则有差异矩阵D=A-A1,则D的Frobenius 范数为,两个状态矩阵的相似度为

式（29）中：差异矩阵的范数值越小,状态矩阵A和A1 之间的相似度越高,同理,权重矩阵Q的更新方法亦是如此,更新方法制定完成后需选择相应的更新阈值,当相似度小于阈值,则更新权重矩阵与状态矩阵,反之,则不更新矩阵,考虑到计算量与精度的要求,本文设置的更新阈值为0.8.

4 仿真与分析

为了验证本文规划的参考路径与控制器的有效性,使用MATLAB/Simulink 与Carsim 进行联合仿真测试,仿真采用的车辆参数为软件内部车辆模型,具体参数如表3 所示.

表3 车辆参数Tab.3 Vehicle parameters

选取车位尺寸为[7.5 m,2.5 m],计算得出以后轴中心为参考点的参考路径与路径曲率,如图8 所示.

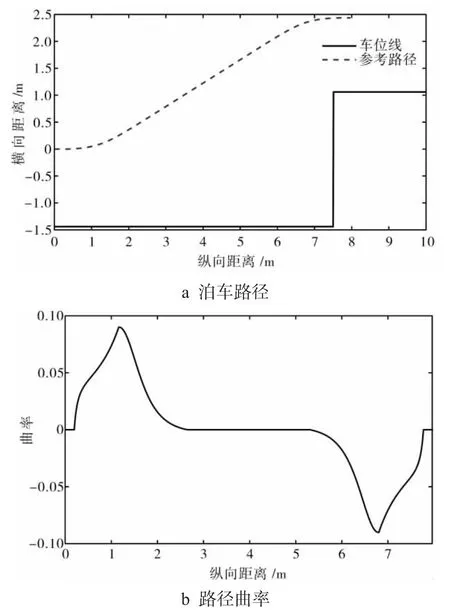
图8 参考路径Fig.8 The reference path

从图8 可以看出规划的泊车路径满足车辆避障约束且路径曲率连续,保证了泊车过程中方向盘转动连续且平顺.由于仿真软件以前轴中心为参考点,因此取控制点P1 的坐标为（2.91,0）,则各控制点的坐标见表4.

表4 控制点坐标Tab.4 Control point coordinates

引入更新机制后,在设计的程序中加入tic 函数,得到更新前后程序运算的时间,如图9 所示.

图9 程序运算时间Fig.9 Program operation time

由图9 可知,引入更新机制前,从整体上来看,程序运算的时间在2.5 ms 上下波动,加入更新机制后,程序运算时间约为0.2 ms,程序运行效率提升了92%,因此,在降低人工调整参数成本的同时,控制器的实时性有所提升.

设定速度为1 m/s,对优化后控制器的性能进行仿真验证,具体仿真结果如图10 所示.

图10 仿真结果Fig.10 Simulation results

结合图10-a,可以发现跟踪误差最大约为0.15 m,在泊车起始阶段与即将进入车位的阶段,车辆产生的跟踪误差较大,在最终驶入车位后,车辆与预定位置相差约0.13 m.分析泊车过程中产生较大跟踪误差的原因是设计模糊逻辑算法的过程中,模糊词汇数量选取较少,导致控制器的跟踪精度下降.对于横摆角误差,从图10-b 中可以看出车辆横摆角误差最大约为0.08 rad,角度误差较小,车辆停止时与车位的夹角约为0.03 rad,近似与车位平行.图10-c 为车辆的前轮转角,从图中可以看出车辆的前轮转角变化连续且较为平顺,然而在最后阶段前轮转角出现小范围的波动,分析后可知在泊车最后阶段车辆调整车身角度的时候出现误差.

图11 为Carsim 中展示的动态泊车过程,图中可以看出,虽然行驶过程中出现跟踪误差,然而并未与障碍车辆出现碰撞,可以完成安全无碰撞的泊入车位的要求.

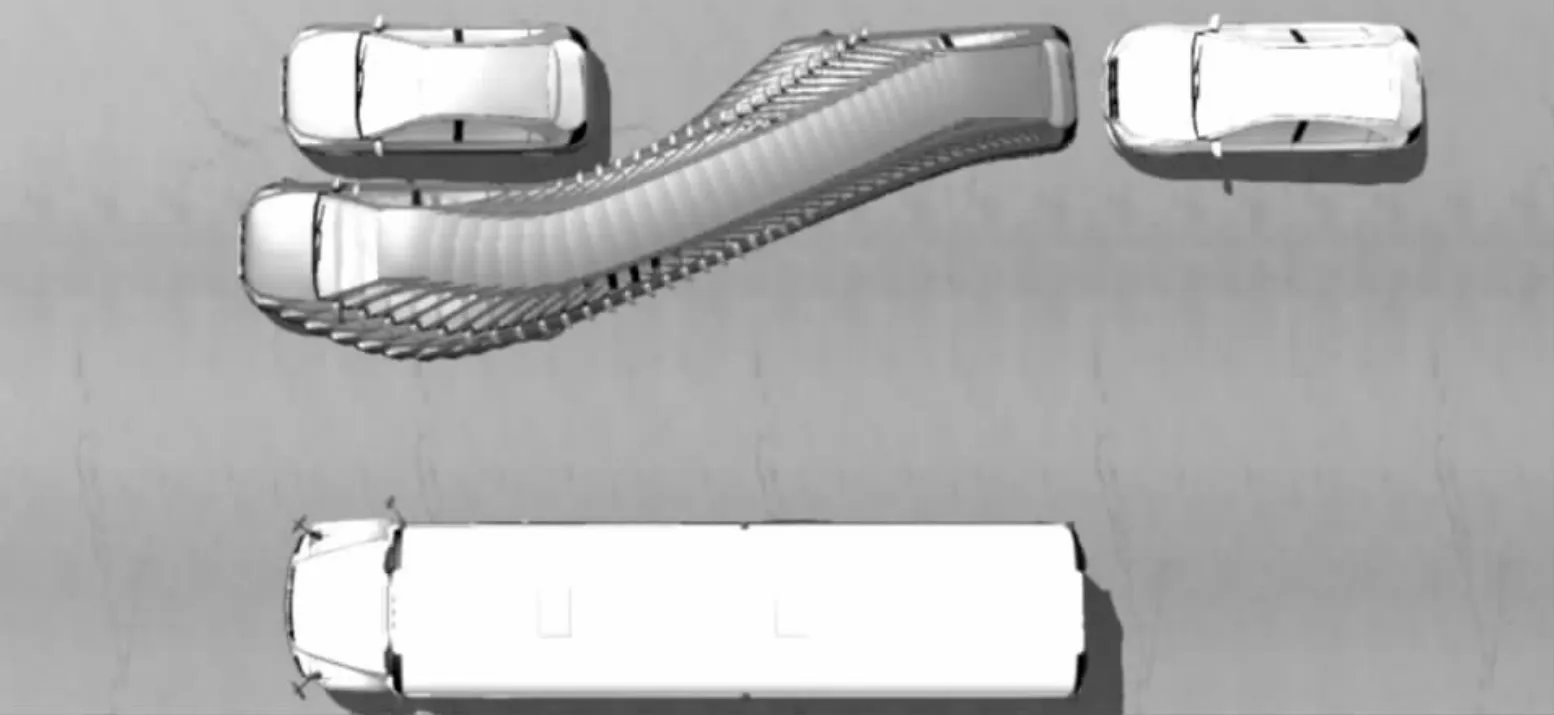
图11 路径跟踪图Fig.11 Path tracking

图12 为优化前后,在不同速度条件下控制器的跟踪结果,对比图12-a 与b 中的跟踪误差与横摆角误差,得出优化后的跟踪误差降低了约30%,横摆角误差降低幅度较小,表明优化后的控制器提升了在不同速度的泊车场景的适应度.

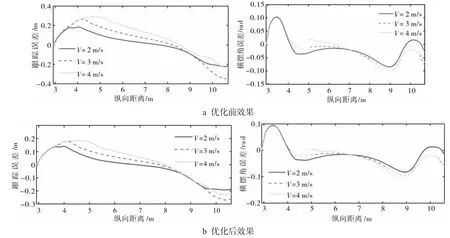
图12 控制器适应度仿真结果Fig.12 Simulation results of controller fitness

5 小结

首先,针对两段圆弧式参考曲线曲率不连续的问题,使用B-spline 曲线计算出一条曲率连续的路径,仿真结果表明规划路径曲率连续,满足泊车需求；其次,结合车辆动力学模型与LQR 理论设计出线性二次型控制器,利用模糊逻辑算法优化控制器,解决了人工调整参数耗时耗力的问题；最后,引入相似度的理论,提升控制系统的实时性与不同速度条件下的适应度,使用MATLAB 与Carsim 进行联合仿真测试,仿真结果表明,优化后控制器的运算速率由改进前的2.5 ms 变为改进后的0.2 ms,运算效率提升了92%,同时改进后的控制器在不同速度下的跟踪误差相较于改进前的降低了约30%,因此改进后的控制器的适应度提升了30%.