基于PSO 优化ELM 模型的震后直接经济损失评估

陈韶金，翟笃林，周 浩，江 颖,，刘子维,

（1. 防灾科技学院, 河北 廊坊 065201；2. 中国地震局地震研究所, 武汉 430071；3. 引力与固体潮国家野外观测研究站, 武汉, 430071）

0 引言

中国地处于环太平洋地震带与欧亚地震带之间，地震活动十分频繁，破坏性的地震往往会造成巨大的人员伤亡和经济损失。但随着社会经济的发展和科学的进步，震后人员伤亡日益减少，但经济损失日益增加，因此震后的直接经济损失评估也逐渐成为全世界关注的热点问题。震后直接经济损失评估不仅仅可以为降低经济损失和制定应急预案提供方案，而且更重要的是为震后经济恢复提供策略支撑。地震发生后，政府需要快速对地震造成的危害和风险程度进行评估，及时掌握震后的损失分布情况，依据震后直接经济损失的大小来决定应急预案准备，以便有效地安排救灾规模和部署救援力量。

传统的震后直接经济损失评估方法错综复杂[1]，且在实际调研中一些影响因素的数据难以获取，给震后评估带来了极大的挑战。随着神经网络的盛行，其在非线性拟合中表现突出，研究人员也将其应用到震后直接经济损失评估中。2007年，马亚杰等[2]选取7 个评估指标建立了震后经济损失快速评估的三层BP 神经网络模型；2014年，Edy 等[3]提出一种FNN 网络模型与GIS 相结合的震后建筑经济损失评估模型；2015年，蔡友军等[4]结合震级-震中烈度的分布规律构建了贝叶斯震后直接经济损失快速评估模型；2016年，赵士达等[5]提出了基于LM-BP 神经网络的震后直接经济损失评估系统，实验表明LM-BP 网络具有精度高和泛化能力强，能够有效评估震后直接经济损失；2017年，谢家智等[6]筛选出8 个评估指标，对比了传统的BP 神经网络和随机权神经网络模型，实验结果表明：随机权神经网络在训练时间、训练精度以及预测精度上都优于BP 神经网络；2021年，郑韵等[7]构建了Elman 神经网络地震经济损失快速评估模型，该网络的预测误差率要远低于单机版地震灾害评估系统；2022年，Zoran 等[8]提出了一种基于随机森林损伤分类模型和代表性抽样算法的快速地震损失评估新框架，使用2010年塞尔维亚克拉列沃地震数据集举例验证所提出的模型。

上述研究主要是利用神经网络机器学习模型对震后直接经济损失进行建模。虽然上述学者提出的网络都有着良好的非线性拟合效果，但是提出的网络模型都具有学习速度慢，容易陷入局部最优等缺点。2004年，Huang 等[9-10]提出一种新型的单层前馈神经网络，该算法被称为极限学习机（Extreme Learning Machine, ELM）。相比于传统的BP 神经网络，ELM 网络的初始权重随机生成后不再对其进行更改。因此，ELM 有着学习速度快、精度高、参数设置简单等优势。但是权重随机初始化将对网络造成不稳定性，因此本文将对ELM 模型进行改进，通过粒子群优化算法(Particle swarm optimization,PSO)对ELM 初始权重进行优化，可避免网络陷入局部最优。将PSO 优化后的ELM 网络应用到震后直接经济损失评估中，可为震后直接经济损失快速评估提供一种新的方法。

1 基本原理

1.1 粒子群优化算法(PSO)原理

受到鸟群觅食行为的规律性启发，James Kennedy和Russell Eberhart 等[11-12]建立了粒子群优化算法(Particle Swarm Optimization，PSO)。在模型中，粒子通过群体信息的共享和更新不断向优化目标方向飞行。

其中，粒子速度、位置更新公式如下:

式中：amax和amin分别表示惯性权重系数的最大值和最小值；t为当前迭代次数；Tmax为最大迭代次数。

1.2 极限学习机(ELM)原理

ELM 本质上是一种单隐含层的前馈神经网络，其初始权重和偏置项可随机生成，训练过程中不需要反向传播进行修改，只需确定隐含层节点个数和激活函数就可以计算输出矩阵，因此该网络具有较强的适应性和极快的训练速度等特点。其单隐含层的前馈神经网络拓扑结构见图1。

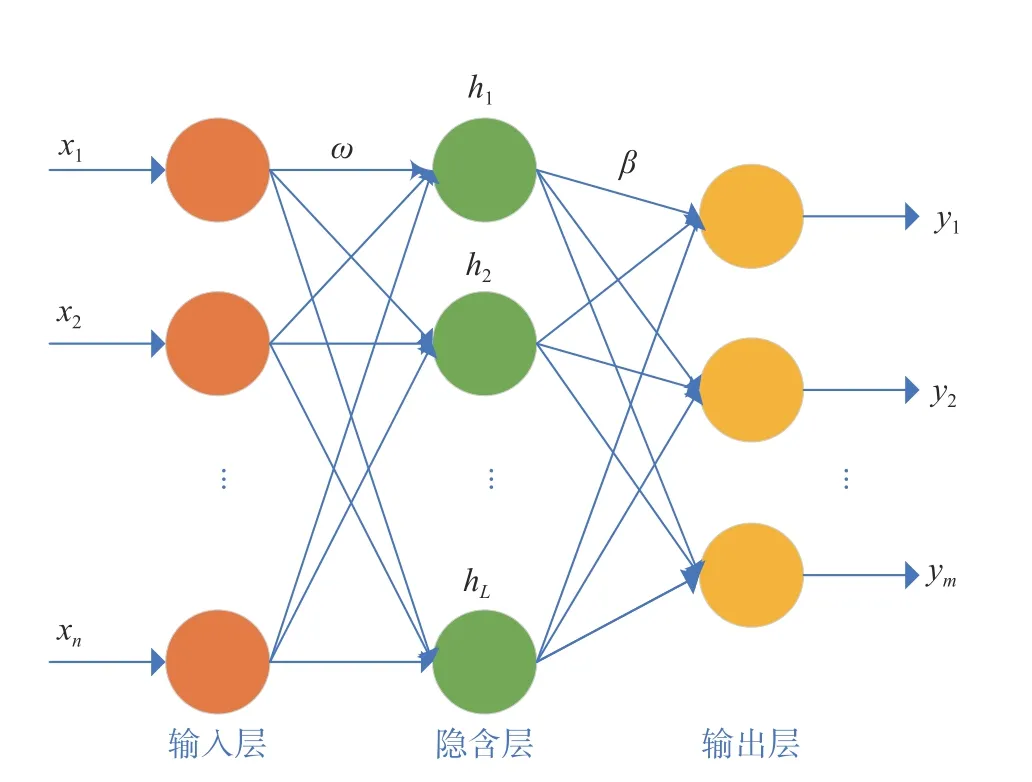
图1 ELM 神经网络拓扑结构Fig. 1 ELM neural network topology

设有N个样本数据集，对于n个输入节点、L个隐含层以及m个输出节点的单隐含层神经网络可以下列式子表示：

式中：ti表示ELM 模型的期望输出；ωk=[ωk1,ωk2,...,ωkn]表示为输入层到隐含层的权重矩阵；βk=[βk1,βk2,...,βkm]表示为隐含层到输出层的输出权值；bk表示为隐含层的偏置项；g(x)表示激活函数。

则ELM 的矩阵表达式为

式中：H表示为隐含层的输出矩阵；β表示为隐含层到输出层的权重矩阵；T表示为模型输出矩阵。

由于ELM 网络模型中的初始权重确定后将不再发生改变，因此ELM 的学习目标可转化为使输出误差最小，此时β可通过公式（6）的最小二乘法求解得到。

通过矩阵运算，可得β的最佳解为

式中：H†表示为矩阵H的广义逆矩阵。

2 震后灾害评估指标选取

2.1 数据来源

从相关文献[7,14-16]中收集和整理了1996—2014年间的37 个地震震例数据（表1），其中32 个地震直接经济损失样本数据作为训练集，5 个数据（震例3、5、11、30、33）作为测试集。由于震后直接经济损失的数值离散且跨度较大，为了更加直观对比预测值与真实值的结果变化，本文采取以e为底的自然对数对震后直接经济损失值进行处理。 其中，ΔL表示震中烈度和抗震设防烈度之差。

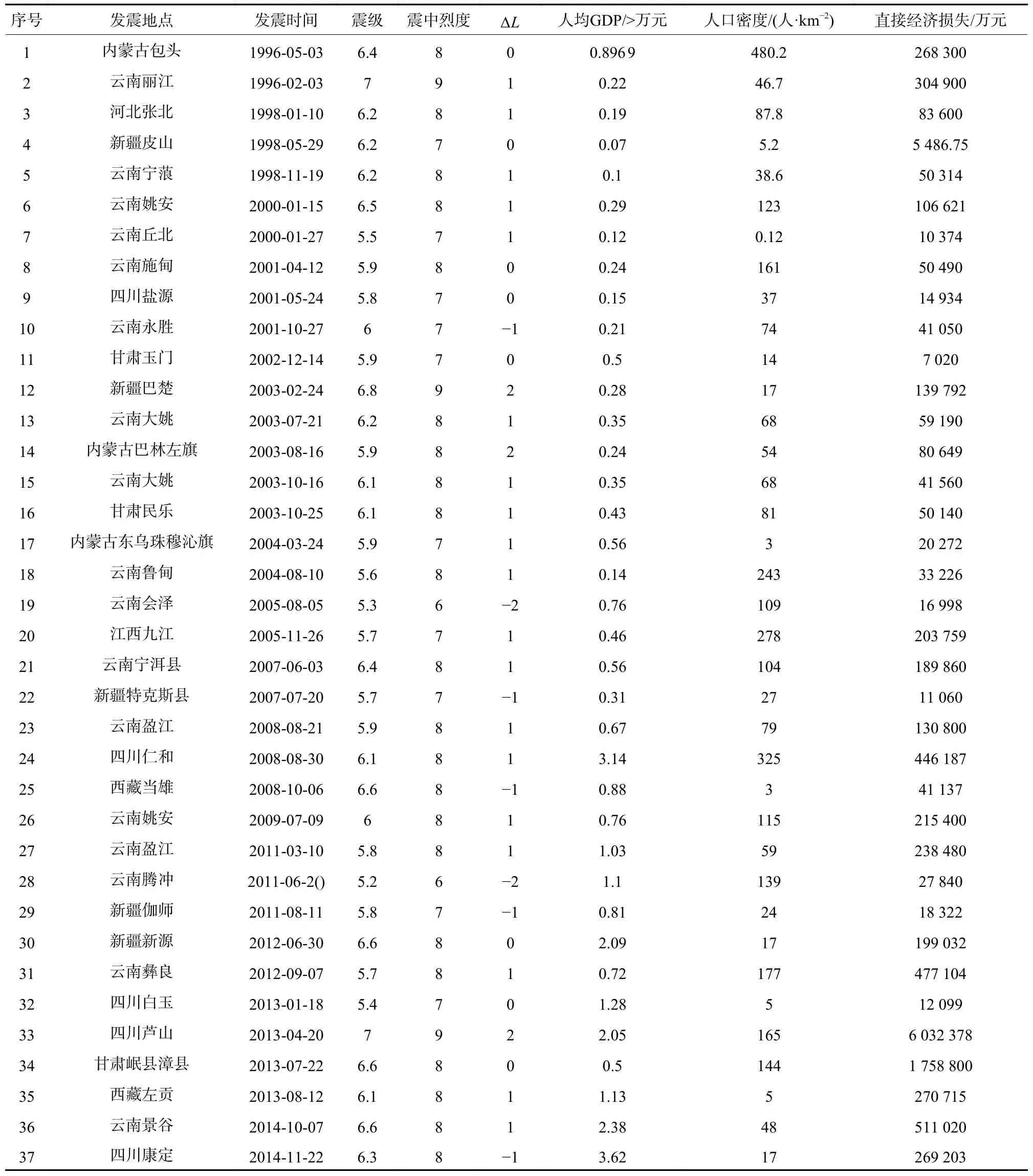
表1 地震直接经济损失样本集Table 1 Sample set of direct economic loss caused by earthquake disaster

2.2 影响因子的选取

影响震后直接经济损失的评估错综复杂，其主要由地震致灾因子、抗震设防因子以及社会经济指标因子3 个部分构成[5]。本文从数据获取难易和重要性角度综合考虑，选取震级、震中烈度、震中烈度和抗震设防烈度之差ΔL、人均GDP、人口密度等5 个影响因素作为评价指标。

地震震级是表明地震强弱的度量。一般来说，地震震级越大，其破坏力越强，对地面建筑物的破坏程度越大，最终造成直接经济损失也越大。震中烈度是指地面受到地震振动作用的强烈程度。同等震级大小条件下，震源深度越浅，震中烈度可能越大。因此，选取震级、震中烈度作为地震致灾因子的评估指标。

抗震设防烈度[17]是指在工程建设时对建筑物进行抗震设计的地震烈度。通常情况下，抗震设防水平越高的地区，同等地震条件下造成的直接经济损失越少。震中烈度和抗震设防烈度之差ΔL体现建筑物抵御地震破坏的能力，如果ΔL＞0，且两者差值越大则说明建筑物抗震能力越弱，地震造成的直接经济损失也越大；如果ΔL＜0，且两者差值的绝对值越小，表明建筑物破坏程度越严重，地震造成的直接经济损失也越大。因此，选取震中烈度和抗震设防烈度之差ΔL作为抗震设防因子的评估指标。

人均GDP 能够较合理地反映了震区的社会财富和经济发展水平，同等破坏性地震条件下，人均GDP 越高的地区，直接经济损失可能越大。而人口密度与地震直接经济损失呈正相关，地震发生在人口密度大的地区，所造成的直接经济损失远大于人烟稀少地区。因此，选取人均GDP 和人口密度作为社会经济因子的评估指标。

3 震后直接经济损失预测模型

3.1 算法流程

本文提出的PSO-ELM 的预测模型流程（图2）分为3 个阶段。①数据预处理阶段：收集历史地震直接经济损失样本集，对影响因子进行筛选，并对原始数据进行无量纲归一化处理；②粒子群算法寻优阶段：将归一化后的数据作为 PSO-ELM 预测模型的输入，设置PSO 优化算法中的粒子初始速度和位置、ELM 中隐含层节点个数和模型终止条件等参数，通过优化算法对网络的初始权重进行优化；③ELM 网络训练阶段：将PSO 优化好的初始权重带入ELM 模型进行网络训练并对其预测结果进行分析讨论。

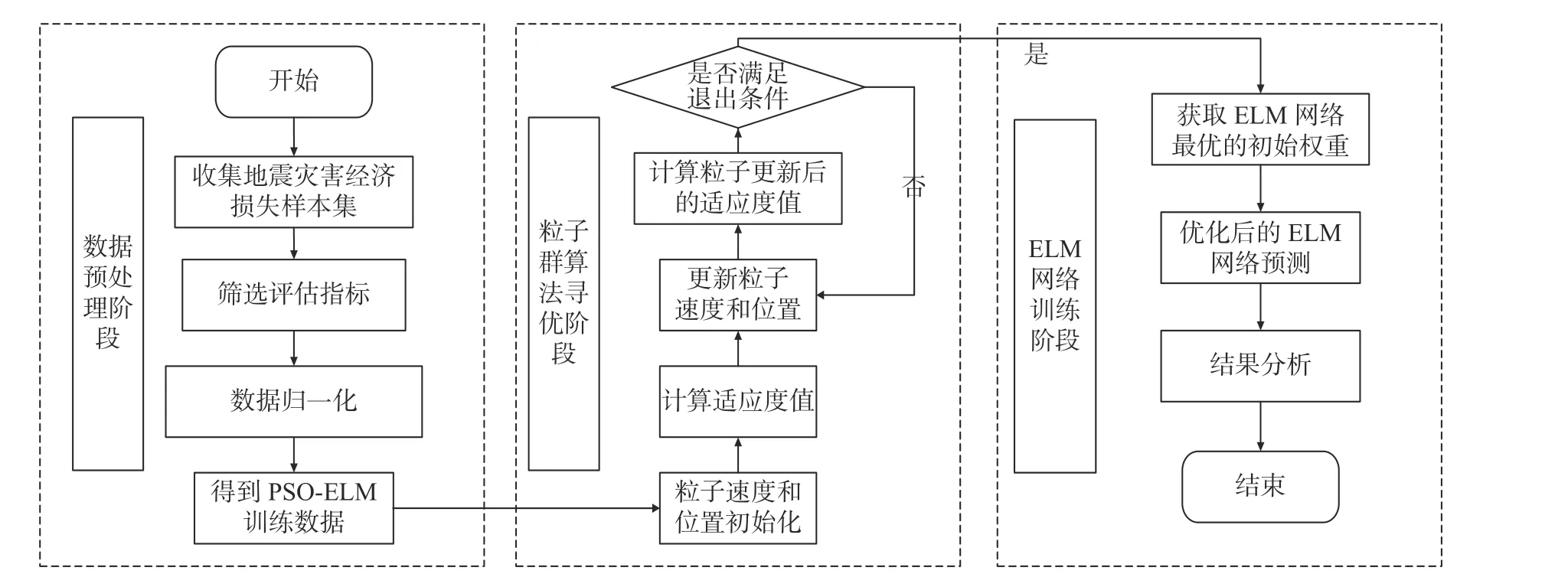
图2 PSO-ELM 模型流程图Fig. 2 PSO-ELM Model Flow Chart

3.2 模型建立

由于地震直接经济损失样本集中的数据单位不统一且取值范围相差很大，因此需要对样本中的数据进行无量纲处理，并将数据取值范围压缩到[0,1]区域内。本文使用最大最小值归一化对5 个评价指标的原始数据进行标准化处理。

式中：Xmax、Xmin分别表示为每个评估指标数据的最大值、最小值；分别表示为某个评估指标的数据和对应的归一化后的数据。

样本数据均为正数，可选取sigmod函数作为ELM 网络模型的激活函数。本文选取震级、震中烈度、震中烈度和抗震设防烈度之差ΔL、人均GDP、人口密度等5 个评估指标作为网络的输入层节点，震后直接经济损失为输出层节点，隐含层节点个数采用经验公式[18]

式中：Ny为隐含层节点个数；p为输入层节点个数s为输出层节点个数；q为[1,10]之间的常数。；

构建好网络模型之后，为了对比3 种模型的整体预测精度和计算影响因子对震后直接经济损失的敏感程度，选取平均相对误差率（ARE）和均方根误差（RMSE）2 个模型评估指标进行评判预测结果的精确度。其计算公式如下：

式中：n为样本数量；yi为真实值；y′i为模型预测值。

3.3 实验结果及分析

随机选取样本3、5、11、30、33 作为测试数据检验模型的准确性。经过多次实验对比，可得到最佳的隐含层节点个数和模型参数（表2）。同时，为验证PSO-ELM 模型的精确度和泛化能力，在保证相同训练样本和隐含层节点个数的前提下，将5 个测试数据经过归一化处理后分别带入到BP、ELM 和PSO-ELM 模型中进行实验并进行结果分析对比。实验结果表明：PSO-ELM 模型训练集和预测集平均误差率最低。图3 为三种模型训练集预测值与真实值对比结果。由图3 可以看出，除个别预测值是BP 和ELM 模型拟合较好之外，整体上看，本文提出的PSO-ELM 模型拟合效果最佳。图4 为3 种模型测试集预测值与真实值对比结果。由图4可以看出，PSO-ELM 模型预测值与真实值最接近。表3 为模型平均误差率的结果对比。

表2 PSO-ELM 网络最佳参数Table 2 Optimal parameters of PSO-ELM network

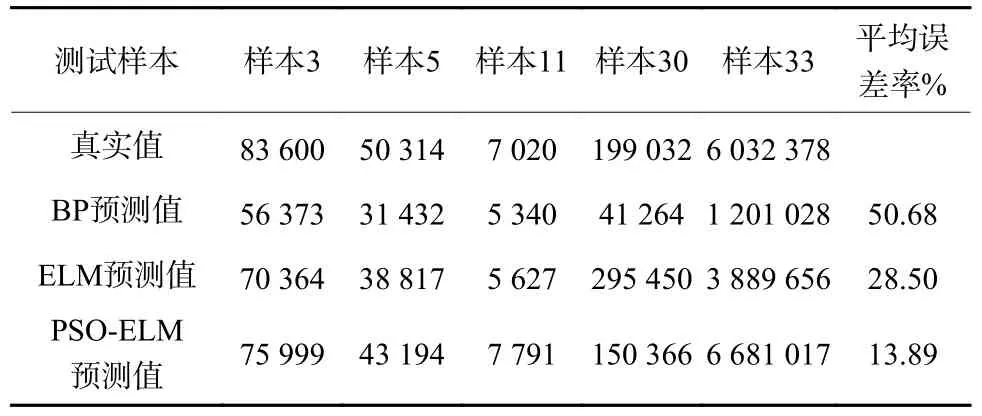
表3 三种模型平均误差率结果对比Table 3 Comparison of average error rate results of three models

图3 三种模型训练集预测值与真实值对比Fig. 3 Comparison between the predicted and the true values of three model training sets

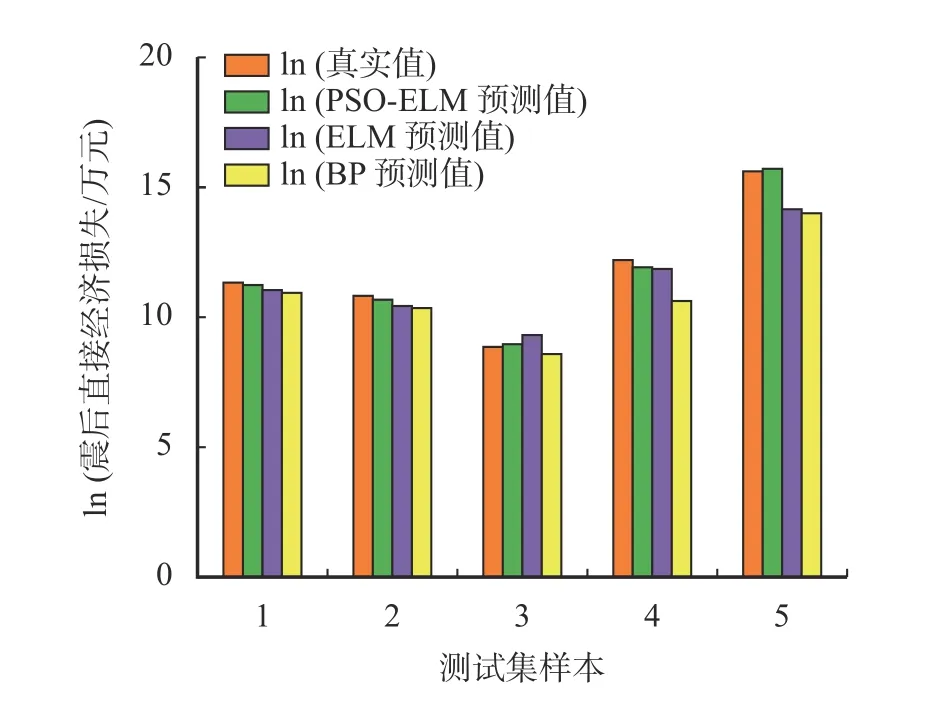
图4 三种模型测试集预测值与真实值对比Fig. 4 Comparison between the predicted values and the true values of three model test sets

由表3 的对比结果可知，传统的BP 神经网络模型预测平均误差率为50.68%，而ELM 模型预测平均误差率较前者减少了22.18%，说明ELM 模型的非线性拟合程度更好。本文提出的PSO-ELM 模型的平均误差率为13.89%，比未经过PSO 优化的ELM 模型精度提高了14.61%，说明经过PSO 优化的模型可避免网络陷入局部最优，并找到全局最优的模型参数解，进而提高模型的精度。因此PSOELM 模型具有较强的稳定性和泛化性，可在震后直接经济损失预测等实际地质灾害评估问题中进行推广应用。

4 敏感性因子分析

本文采用敏感因子分析方法[19]进行计算各影响因子对震后直接经济损失的敏感程度。为了保证敏感性因子分析的准确度，需要确保数据集划分和PSO-ELM 模型的网络参数设置一致前提下，将5 个输入层的影响因子逐一减少，构建对应的5 个4 影响因子输入PSO-ELM 的震后直接经济损失评估模型。根据预测集结果的平均相对误差率ARE和均方根误差RMSE进行计算影响因子的敏感程度，计算公式如下：

式中：R1i与R2i表示敏感指数；AREi和RMS Ei分别表示缺少第i因素的平均相对误差和均方根误差。若R1i＞R1j，说明i影响因素比j影响因素对震后直接经济损失的精确性影响更加敏感；若R2i＞R2j，说明i影响因素比j影响因素对震后直接经济损失的稳定性影响更加敏感；R1i和R2i的值大于或接近1 说明该影响因素对于震后直接经济损失影响强烈，其值小于1 则说明该因素影响微小。实验对比结果见表4。

表4 敏感性分析实验对比结果Table 4 Comparison results of sensitivity analysis experiment

由表4 可知：5 个影响因子的R1和R2都大于1，说明筛选的影响因子都会对震后直接经济损失造成不同程度上的影响。其中人均GDP、人口密度和震中烈度对震后直接经济损失的敏感指数最大，对应的R1值为4.7588、3.7368 和3.4921，R2值为5.2924、4.2396 和3.2968，说明人均GDP、人口密度和震中烈度对震后直接经济损失影响程度最大，而其他影响因子对震后直接经济损失敏感性较弱，对其影响程度较小。综上所述，在研究震后直接经济损失评估时，人均GDP、人口密度和震中烈度可作为重点研究影响因素，评估过程中应该对其进行重点研究，可为震后损失评估与应急管理提供参考。

5 结语

震后直接经济损失精准评估在应急管理方面具有重要而深远的意义。由于影响震后直接经济损失的影响因子错综复杂，理论上考虑所有影响因子的评估系统才是最佳的。但是在实际调研实验过程中，很多数据记录不全或难以获取，对评估指标的选取造成了巨大的挑战。本文为了科学准确地解决震后直接经济损失评估的实际问题，综合多方面因素考虑，选取了震级、震中烈度、震中烈度与抗震设防烈度之差（ΔL）、人均GDP、人口密度等5 个影响因子作为模型的输入特征。通过实验对比BP、ELM 以及PSO-ELM 三个预测模型得出了以下结论。

1）本文提出的PSO-ELM 模型可由粒子群智能优化算法对ELM 网络的初始权值进行优化，可加速网络收敛能力和获取全局最优解。相较于传统的BP 网络和未优化的ELM 网络，PSO-ELM 模型的预测值与真实的震后直接经济损失值平均误差率最小，因此该评估方法具有一定的实际应用价值，可为震后快速评估直接经济损失提供一种新的研究方法。

2）在震后直接经济损失评估中，人均GDP、人口密度和震中烈度是直接经济损失的主要敏感因子。因此，在实际震后直接经济损失评估中，应对这三大影响因子进行重点分析和研究。

由于筛选的样本数据的震级都是在5 级以上的，对于震级低于5 级的震后直接经济损失评估未来还需要进一步实验研究。