P2PSand 和Finn 本构模型在水库土石坝液化模拟中对比

2024-01-20牛金帝张西文陈子俊

华北地震科学 2023年4期

牛金帝，张西文，邱宇，扈萍，陈子俊

（济南大学土木建筑学院, 济南 250022）

0 引言

自17 世纪至今，山东境内及周边地区已发生15 余次强地震。多数土石坝建于20 世纪80年代，由于当时技术水平落后，修建土石坝时并未考虑坝基砂土液化的影响，导致土石坝在地震发生时发生较大危害，出现滑坡、震陷等问题，因此进行土石坝动力响应研究是非常有必要的。

土体的动力分析方法根据本构模型可分为基于等价粘弹性的等效线性分析方法和基于(黏)弹塑性模型的非线性分析方法。等效线性分析方法是用一个等效的剪切模量和阻尼比代替所有不同应变幅值下的剪切模量和阻尼比，将非线性问题转化为线性问题，利用频域线性波动方法求解[1]。但是等效线性分析方法存在不能反映土层中真实的运动过程，在地震动输入较大时计算误差较大，可能出现死循环现象等问题。若想得到真实的土体地震反应，宜采用基于(黏)弹塑性模型的非线性分析方法。非线性分析方法将土体视作为（黏）弹塑性变形材料，模型由初始加荷曲线、移动的骨干曲线和开放的滞回圈组成。该模型能更好地模拟残余应变，进行动力分析时可以直接计算残余变形，在动力分析中可以随时计算切线模量并进行非线性计算，这样得到的动力响应过程能够更好地接近实际情况[2]。

在有关岩土地震的工程实践中，基于(黏)弹塑性模型的非线性分析方法被广泛运用于模拟砂类材料的液化现象，例如MD97 模型[3]、DM04 模型[4]，以及在此基础上拓展的Sanisand 模型[5]、UBCsand模型[6]、PM4sand 模型[7]等。DM04 模型需要高准确性的实验室测试数据且不具备液化后刚度退化的机制，因此在其基础上进行改造并建立了双塑性面砂土模型P2PSand 模型。该模型具有DM04 模型理论的稳健性和简明性，以及UBCsand 模型和PM4sand 模型面向实践的特性。P2Psand 适用于一般的三维条件，P2PSand 模型参数适用于标准循环阻力场砂土，与半经验过程中的循环阻力图兼容，且该模型允许用户指定自定义参数，而非默认材料参数[8-10]。

土体是非线性材料，地震动力越大，则土体的非线性特征越强，因此研究土石坝动力响应应采取非线性分析方法，双塑性面砂土模型Practical Twosurface Plastic Sand (简称P2PSand）模型[11-12]与Finn本构模型均采用非线性分析方法。基于P2PSand 本构模型，Zhao C 等[13-14]在DM04 模型上修改了一些公式，并保留了一般的三维公式，模拟结果与实验数据以及不同初始和加载条件下的经验关系吻合较好，从而提高了模型的性能；吴宏[15]等采用三维数值方法研究穿越不同密实度状态饱和砂土地层的盾构隧道的地震响应规律。基于Finn 本构模型，胡南雄等[16]对某中型水库大坝坝基可液化土层进行数值模拟，分析了不同库水位作用下坝基可液化土层的孔隙水压力变化过程及坝体典型节点的动力响应；严祖文等[17]分析坝基土及大坝整体抗震稳定，并根据研究成果提供合理可行的防震措施、供水库加固设计与施工应用；李伯根等[18]对大后沟尾矿堆积坝进行地震动力响应分析并进行液化评价，分析其动力稳定性，以指导尾矿库的安全运行。P2PSand 本构模型是于2019年新开发的本构，国内对该本构的应用研究较少，因此本文将采用FLAC3D 7.0 内置P2PSand 本构模型与Finn 本构模型进行数值模拟，从而得出不同本构模型下的土石坝动力响应特征，找出土石坝最薄弱区域，为土石坝抗震除险加固提供理论依据。

1 工程概况

本文计算模型以山东某水库土石坝为背景，该水库土石的模型及监测点分布如图1 所示。该大坝底端固定，两侧水平方向固定，竖直方向自由，地震波由底部输入。计算监测变量为监测点A的超孔压比，监测点B的竖向位移，监测点C的水平位移等。该水库土石坝材料参数如表1 所示。

表1 材料参数Table 1 Material parameters

图1 水库土石坝模型及监测点分布示意图Fig. 1 Reservoir earth-rock dam model and monitoring site distribution diagram

模型边界设置为自由场边界，以此来减少边界对地震波的反射；材料阻尼设置为0.1571；选用FLAC3D 建模，设置土层的材料参数和边界条件，于土石坝底部输入不同峰值强度的地震波，为了保证数值模拟的计算速度和精度，通过滤波把大于10 Hz的高频分量过滤掉，将滤波后的地震动作为基底输入地震动。以峰值为0.2 g 的地震波为例，利用SeismoSignal 软件对原始地震波进行滤波和基线校正，并在模型底部水平施加处理后的地震波（图2）。其中，在FLAC3D 分别设置P2PSand 和Finn 本构模型模拟地震砂土液化现象，在土石坝底部施加峰值强度为0.1 g、0.2 g、0.3 g 强度的地震波，g 为重力加速度，可液化粉砂层相对密实度依次为0.30、0.45、0.70、0.90。

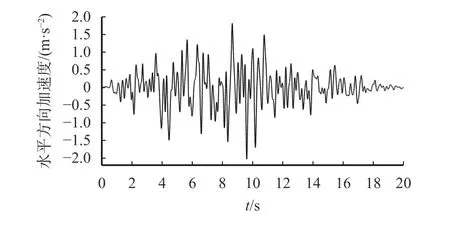
图2 利用SeismoSignal 软件对原始地震波进行滤波和基线校正处理后的地震波Fig. 2 Seismic wave after filtering and baseline correction of original seismic wave using SeismoSignal software

2 土的本构模型

在实际工程应用中，所采用的本构模型不仅要能够准确表达土的应力-应变关系，而且还必须具有形式简单、参数易于确定等特点。P2PSand 本构模型和Finn 本构模型同时具有模型形式简单与参数易于确定的优势，其参数由相对密实度决定；P2PSand 本构模型和Finn 本构模型的其他参数由与相对密实度有关的经验公式取得，相对密实度在工程中容易获取。FLAC3D[19]在进行动力分析时所采用的方法为基于(黏)弹塑性模型的非线性分析方法，遵循Biot 流体-机械耦合孔隙力学理论的应用。

P2PSand 模型由19 个参数控制，其中输入参数3 个，其余参数均为默认值。

Finn 模型是Martin 等根据试验提出的，可用于解决土在循环荷载作用下体积应变以及孔隙水压力的变化规律问题[20]。该模型的实质为在摩尔库伦模型的基础上增加了动孔压的上升模式，并假定动孔压的上升与塑性体积应变增量相关。

Byrne 在实验数据基础上对Finn 模型[21]进行了简化，简化后的计算公式为:

式中：Δεvd为砂土体积剪应变增量；εvd为砂土体积剪应变；γ为剪应变；C1、C2为模型参数。经验计算公式为[21]

表2 给出可液化粉砂层的P2PSand 本构模型与Finn 本构模型参数。由表2 可知，2 个模型参数循环因子Kc、弹性剪切模量Gr、模型参数C1、C2均由相对密实度dr确定。

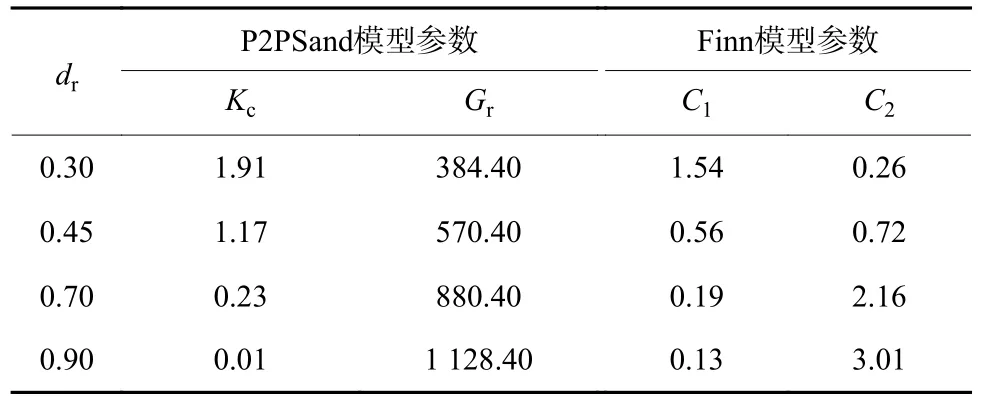
表2 可液化粉砂层的P2PSand 本构模型与Finn 本构模型参数Table 2 P2PSand constitutive model and Finn constitutive model parameters of liquefiable silty sand layer

3 动力响应对比计算分析

3.1 坝基液化分析

为了更直观地反映水库土石坝砂土液化的程度，定义超孔压比excess pore water pressure ratio（epwpr）描述坝基液化程度，对监测点A的超孔压比进行监测，计算公式如下：

当epwpr=1时，说明土体完全液化。工程上当epwpr＞0.6时，饱和砂土地基将产生失效。因此，本文将epwpr=0.6的单元定义为准液化单元，这也是考虑到土石坝的稳定性而做的一种安全储备。图3～5 分别为加速度峰值为0.1 g、0.2 g、0.3 g 地震波输入、相对密实度为0.45 时不同本构模型的超孔压比云图，图6 为加速度峰值为0.2 g 时不同密实度下监测点B超孔压比时程曲线图。由图3～6 可知，当加速度峰值为0.1 g 时，水库土石坝坝基两侧发生液化，坝体下部坝基并未发生液化，随着加速的峰值增大，水库土石坝坝体下部坝基出现砂土液化现象。基于P2PSand 本构下的可液化粉砂层的地震砂土液化程度与范围略大于Finn 本构模型下的程度与范围。两种本构模型下，可液化粉砂层液化的规律相同：t＜4 s 时，超孔压比增长较小；4 s＜t＜16 s时，超孔压比增长逐渐增大；当t＞16 s 时，超孔压比增长趋于稳定。由图3～5 可以看出，两种本构模型下，可液化粉砂层液化的面积与范围相差无几，但液化程度相差较大；P2PSand 本构模型下坝基两侧超孔压比较大数值已接近1.0，处于完全液化，而Finn 本构模型下坝基两侧超孔压比最大数值约为0.7，处于中等液化。由于P2PSand 模型采用了DM04模型理论的稳健性和简明性，以及UBCsand 模型和PM4sand 模型面向实践的特性，因此计算结果更贴近于实际。

图3 0.1 g 地震波下相对密实度为0.45 时不同本构模型的超孔压比云图Fig. 3 The cloud image of over pore pressure ratio under 0.1 g seismic wave action for different constitutive models with the relative density of 0.45

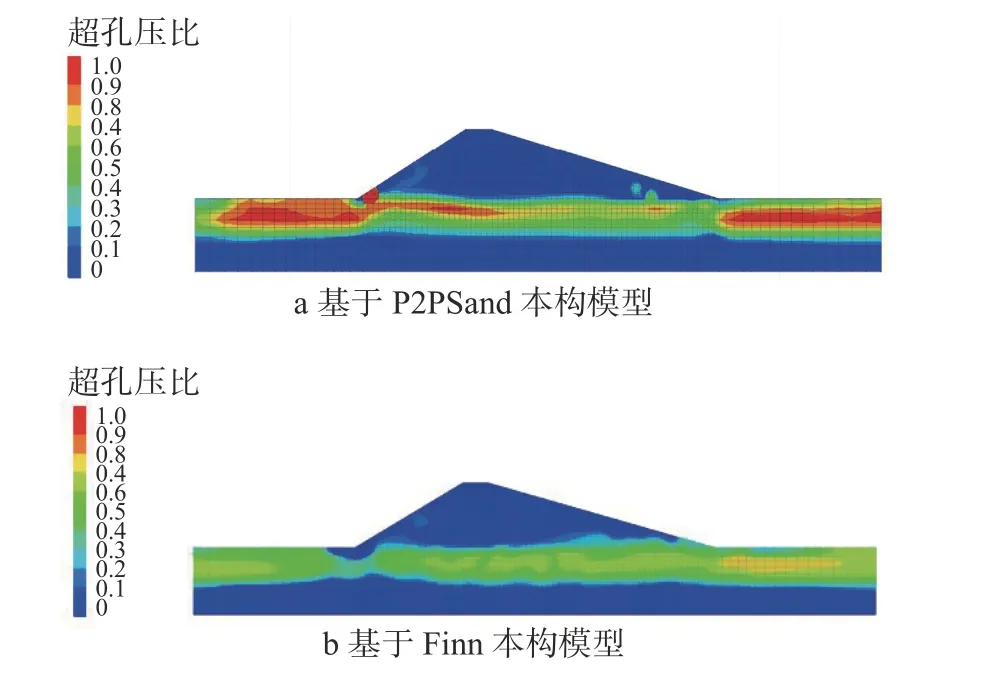
图4 0.2 g 地震波下相对密实度为0.45 时不同本构模型的超孔压比云图Fig. 4 The cloud image of over pore pressure ratio under 0.2 g seismic wave action for different constitutive models with the relative density of 0.45

图5 0.3 g 地震波下相对密实度为0.45 时不同本构模型的超孔压比云图Fig. 5 The cloud image of over pore pressure ratio under 0.3 g seismic wave action for different constitutive models with the relative density of 0.45

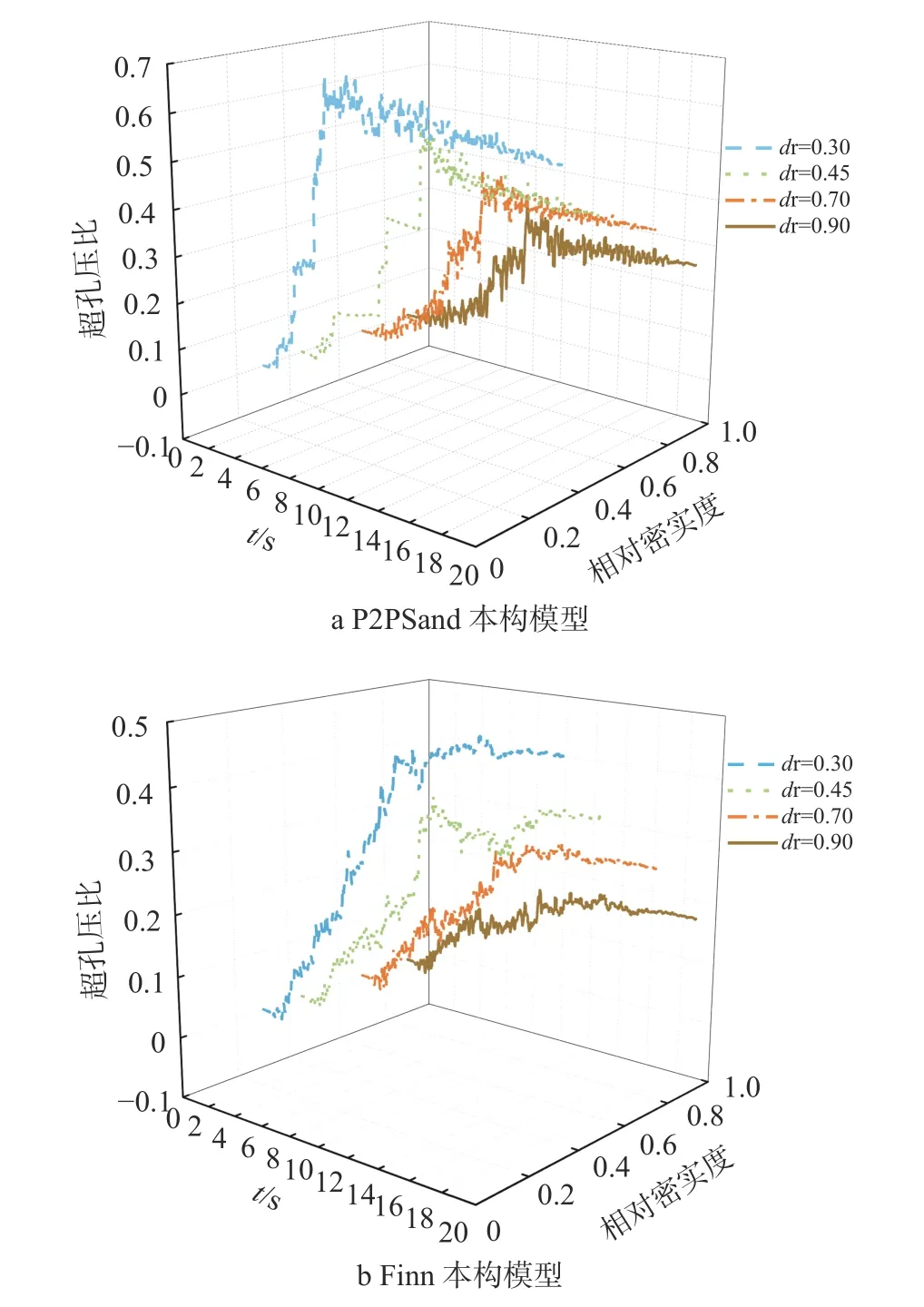
图6 加速度峰值为0.2 g 时不同密实度下监测点A 超孔压比时程曲线Fig. 6 The time history curve of excess pore pressure ratio for monitoring point A under different density is obtained when the peak acceleration is 0.2 g

3.2 坝体变形分析

由图7 不同本构模型下水库土石坝变形云图可以看出，两种本构模型的水平位移均大于竖向位移，且背风坡的水平位移大于迎风坡的水平位移。由图8 中加速度峰值为0.2 g 时不同密实度下监测点B的竖向位移、C的水平位移可知，P2PSand 本构模型下的水平位移远大于Finn 本构下的水平位移而P2PSand 本构模型下的竖向位移略大于Finn 本构模型下的竖向位移。相对密实度为0.3 和0.45时，P2PSand 本构模型下的水平位移约为Finn 本构模型下水平位移的3 倍，竖向位移约为2 倍；相对密实度为0.7 和0.9 时，P2PSand 本构模型下的水平位移约为Finn 本构模型下水平位移的4 倍，竖向位移约为2.5 倍。由图6 可知，P2PSand 本构下的液化速度与程度均大于Finn 模型，因此P2PSand 本构下的位移也大于Finn 模型。

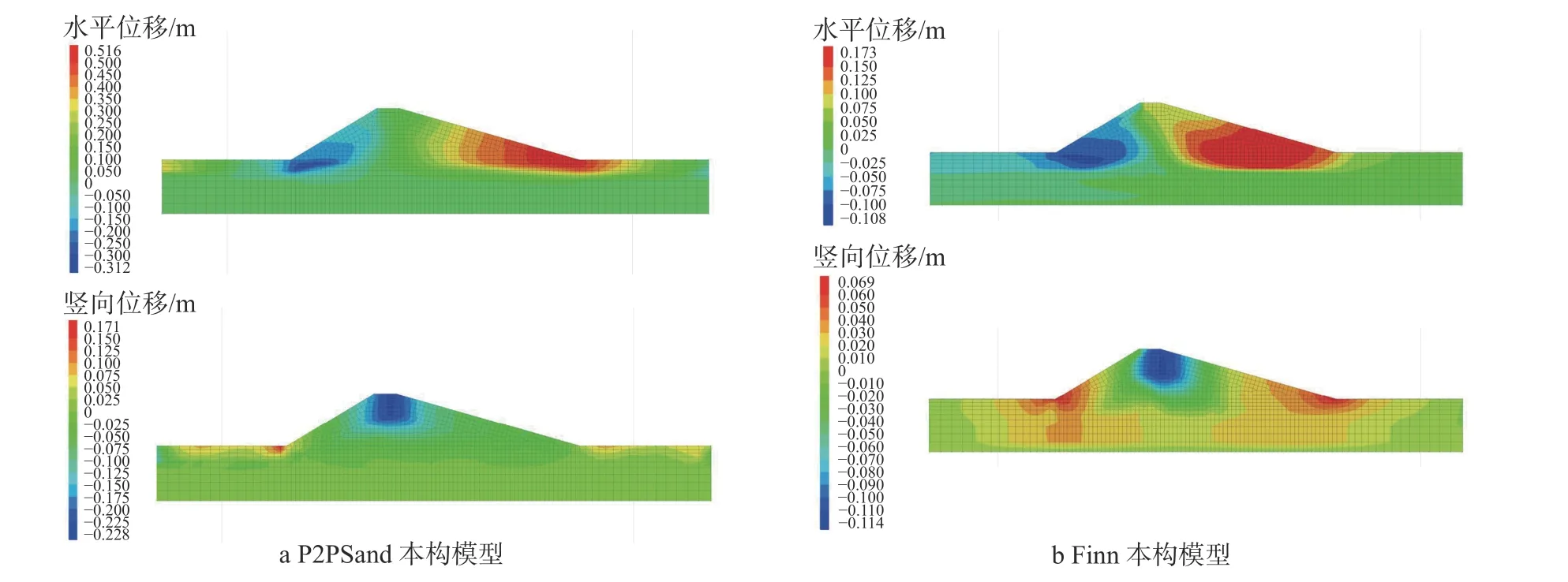
图7 不同本构模型下水库土石坝位移变形云图（0.2 g，dr=0.45，t=20s）Fig. 7 Displacement and deformation cloud map of reservoir earth-rock dam under different constitutive models（0.2g,dr=0.45，t=20s）

图8 加速度峰值为0.2 g 时不同密实度下监测点B 的竖向位移C 的水平位移Fig. 8 When the peak acceleration is 0.2 g the vertical displacement of the monitoring point A and the horizontal displacement of the monitoring point B under different compactness are obtained

3.3 稳定性分析

由图9 可知，水库土石坝在两种本构模型下坝坡均出现两条明显的滑动面，稳定性均降低，且处于P2PSand 本构模型下的水库土石坝最大剪切应变增量约为Finn 本构模型下水库土石坝最大剪切应变增量的2 倍。P2PSand 本构模型下的水库土石坝最大剪切应变增量最大值位于坝基左侧，Finn 本构模型下水库土石坝最大剪切应变增量值位于坝顶。