大型冷库螺杆压缩机几何特征及型线优化研究

王涛，齐强，董艳，张德海，蔡迎军，展登一

大型冷库螺杆压缩机几何特征及型线优化研究

王涛1,2，齐强1，董艳3，张德海1，蔡迎军2*，展登一1

（1.郑州轻工业大学，郑州 450002；2.中国科学院过程工程研究所，北京 100190； 3.北京市科学技术研究院 城市安全与环境科学研究所，北京 100054）

针对大型冷库系统用螺杆压缩机的型线设计与优化问题，建立型线几何特征计算数学模型，为螺杆压缩机型线设计与优化提供理论依据。以目前广泛采用的GHH型线为研究对象，基于本文采用的型线几何特征计算方法，发现GHH型线的接触线不连续。采用圆弧-圆弧包络线共轭曲线对代替原始GHH型线中的圆弧-圆弧共轭曲线对，实现接触线的连续，提出修正的GHH型线。进而以修正的GHH型线为研究对象，分析节圆半径、齿高、双边长度等型线参数对接触线、啮合线、泄漏三角形等型线几何特征的影响。研究发现，泄漏三角形的面积与节圆半径、导程呈线性正相关，与齿高、双边长度呈线性负相关，其中双边长度对泄漏三角形的面积影响最大。具体地，当节圆半径由48 mm增大至60 mm时，面积利用系数由0.462减小为0.427，接触线长度由174.5 mm增大至182.2 mm，泄漏三角形面积由1.7 mm2增大至8.2 mm2。本文建立了转子型线几何特征快速计算数学模型，对GHH型线进行了优化，实现了螺杆转子接触线的连续，揭示了型线参数对型线几何特征的影响规律，为转子型线优化提供了理论指导。

螺杆压缩机；接触线；啮合线；泄漏三角形；GHH型线

在“碳达峰”与“碳中和”的背景下，冷链物流领域的研究重点从大型化转变为高效化[1-3]。螺杆式制冷压缩机以可靠性高、寿命长、气动阻力小、操作简单等优点[4]，广泛应用于大、中型（制冷量在350 kW/h以上）冷库，是冷链物流的核心装备[5-6]。提高螺杆式制冷压缩机的热力学效率和可靠性对保证冷链物流高效节能运行具有重要意义[7]。型线是影响螺杆压缩机性能的关键因素[8]。当前，型线种类繁多，亟需开发一种型线几何特征计算数学模型，分析型线参数对转子性能的影响规律。

许多学者通过优化设计型线和相关几何参数来提高螺杆压缩机的能效。Hanjalic等[9]基于典型转子型线的齿曲线组成成分，以优化机体的运行特性为目标，通过使用离散点拟合的方法设计符合要求的新型型线，并且对该型线的优化方法进行详细介绍。Stosic等[10]通过对转子型线进行优化，改变转子的结构参数。结果表明，优化后的压缩机不仅齿间面积得到进一步扩大，同时接触线长度也进一步缩短，使得其性能获得大幅提升。朱俊杰等[11]通过理论计算发现锥形双螺杆压缩机的排气扭转角度更大，总的扭转角度更小。锥形使得转子接触线长度和泄漏三角面积都有所减小。张炯焱等[12]分析了转子齿数、节圆半径和型线曲线对转子齿顶间隙面积、接触线长度以及泄漏三角形面积的影响。李雪琴等[13]发现在相同情况下椭圆修正的型线的泄漏三角形面积明显小于圆弧修正的型线，泄漏三角形面积减小了27.74%。

除了几何参数的设计及优化外，螺杆压缩机的喷油量、转速、排气压力、吸气参数、温度等工况参数也会影响螺杆压缩机的能效。由于其结构的复杂性，螺杆部件的特性不仅受到热力学基本定律的影响，还受到生产工艺和装置结构的影响，导致难以建立高精度的仿真模型[14]。对双螺杆组件的仿真研究集中在注水润滑[15]、注油[16]、转子间隙[17]、降噪[18]等方面。已有的研究中，研究者分析了型线参数对一个几何特征的影响，没有考虑型线参数对多个几何特征的影响规律。

本文以GHH型线双螺杆压缩机为研究对象，基于所建立的型线几何特性评价方法，提出使用圆弧-圆弧包络线代替原始的圆弧-圆弧的GHH修正型线，提高型线密封性。分析节圆半径、齿高等型线设计参数对啮合线长度、齿间面积与泄漏三角形面积等型线几何特征的影响。

1 型线几何特性计算方法

1.1 型线参数及几何特征

1.1.1 型线参数

型线的绘制需要多个设计参数，包括阴转子节圆半径（p2）、阳转子齿高（i）、双边长度（o）、保护角（）、椭圆长轴半径（）等，如图1a所示。

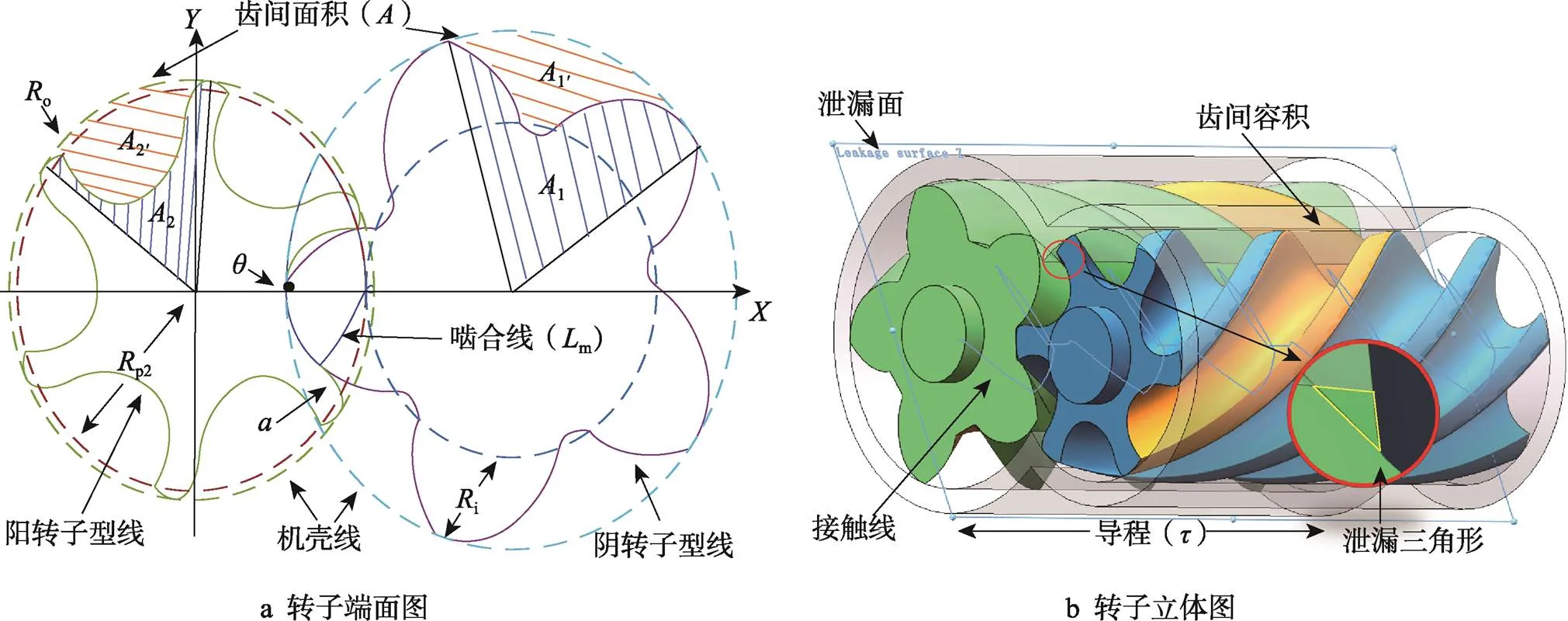
图1 转子型线参数与转子参数

1.1.2 几何特征

螺杆部件的几何特征包括啮合线、接触线、齿间容积、泄漏三角形等参数，如图1所示。其中泄漏三角形的面积、啮合线、接触线的长度值越小代表转子性能密封性越强，面积利用率、齿间容积越大代表转子容积性越好。

1.1.2.1 啮合线

啮合线（m）指端面啮合部位组成的密封曲线，如图1a中曲线所示。表达式为：

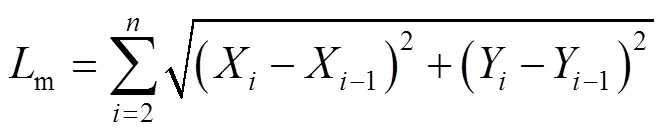
式中：m为啮合线长度；为型线啮合线参数方程；为点坐标个数。

1.1.2.2 接触线长度

接触线（）指转子啮合时两转子齿面接触形成的空间曲线，如图1b中曲线所示，表达式为：

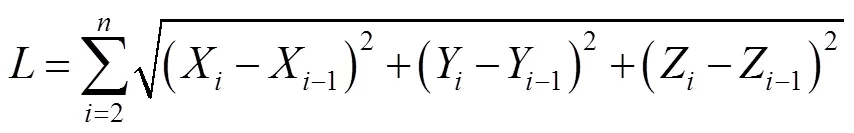
式中：为接触线长度；、为啮合线参数方程；为点坐标个数。

1.1.2.3 齿间面积

齿间面积（）指单个阴、阳转子齿能容纳的气体面积，如图1a所示。表达式为：

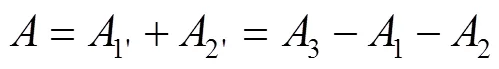
式中：为转子齿间面积；1为阳转子单齿面积；2为阴转子单齿面积；1'为阳转子齿间面积；2'为阴转子齿间面积；3为气缸端面面积。

1.1.2.4 面积利用率

面积利用率（n）指转子直径范围内总面积的利用程度，表达式为：

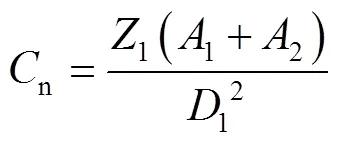
式中：n为面积利用率；为转子齿间面积；1为阳转子齿数；1为阳转子机壳半径。

1.1.2.5 泄漏三角形

泄漏三角形（b）指接触线顶点未能到达阴阳转子气缸孔交线，在接触线顶端与气缸间产生的三角形泄漏通道，如图1b中放大区域的封闭曲线所示，表达式为：

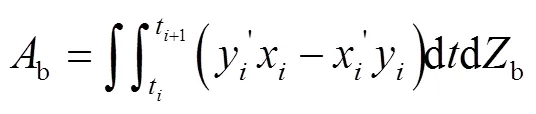
式中：b为泄漏三角形的面积；x、y为型线参数方程；x'、y'为型线参数方程对参数的导数。

1.2 型线组成

为研究型线几何特征的变化规律，选择广泛使用于制冷螺杆压缩机的GHH型线作为研究对象，型线组成见表1，型线如图2a所示。其中，采用点-摆线啮合结构，减小了泄漏三角形的面积，整体呈流线型，从而降低了流阻。为了增大齿间容积，提高整体效率，一般采用6-5齿。

表1 GHH型线组成参数

Tab.1 GHH profile composition parameters

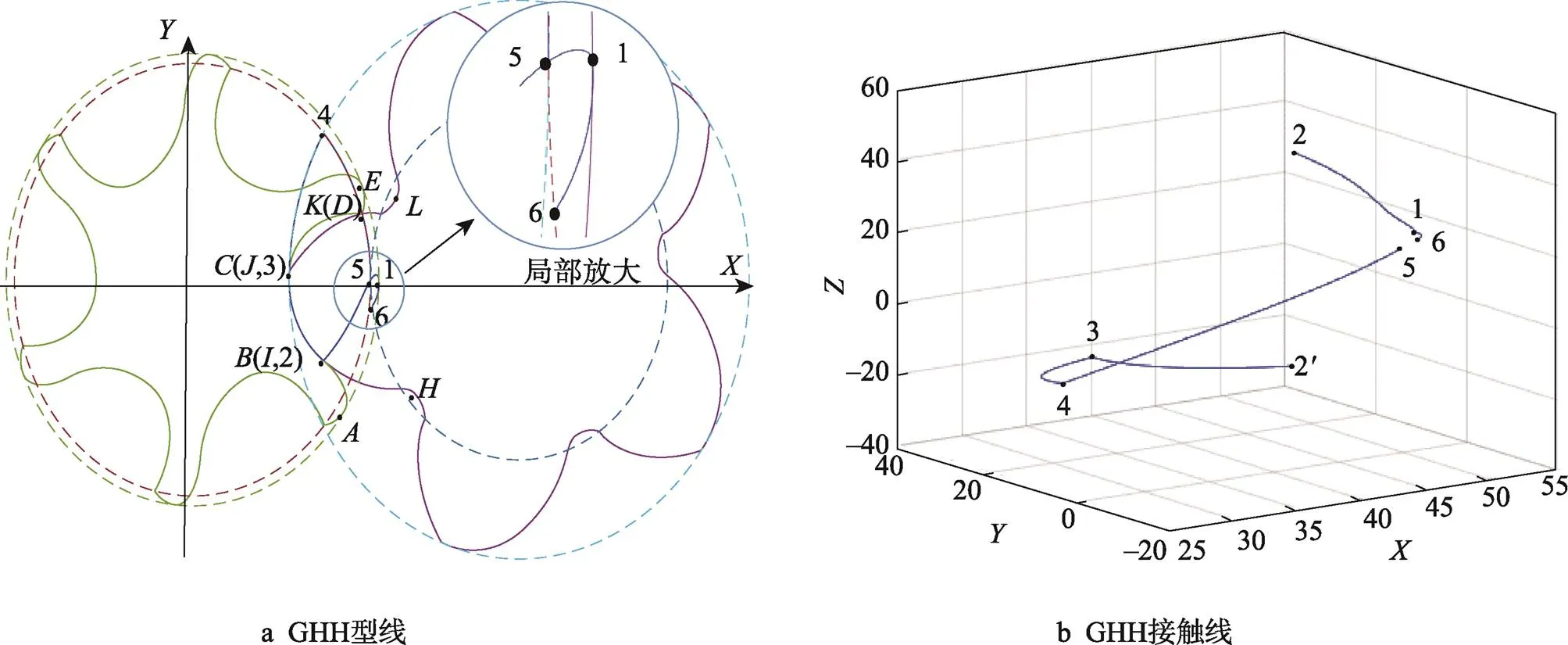
图2 GHH型线与接触线

如图2b所示，GHH型线螺杆转子在空间上的接触线不连续，且啮合线不封闭。这是由于在GHH型线组成线段中，存在点-摆线（-）和圆弧-销齿圆弧（-），其中为2段线段的连接点。根据啮合原理，型线-的啮合线终点5为轴与阴转子的节圆交点，而圆弧-圆弧啮合仅在角度为0°时，实现-整段啮合，其啮合线的起点6为阳转子的气缸圆一点。可以从图中看到，点5与点6不重合。Fleming等[19]指出当接触线不密封时，在压缩机运行过程中，相邻腔室之间气体从高压腔室向低压腔室泄漏，导致压缩机内泄漏严重，无法排出高压气体，降低了压缩机效率。因此有必要对GHH型线进行修正。

为保证啮合线连续，本文对GHH型线-段进行修正，提出使用圆弧-圆弧包络线替代GHH型线的销齿圆弧。GHH修正型线的组成参数见表2，GHH修正型线和接触线图像见图3。

1.3 准确性验证

通过计算不同离散点数下型线的几何特征参数与几何建模软件SolidWorks生成的几何特征进行对比，进行离散点数无关性验证。输入的型线参数如表3所示。

表2 GHH修正型线组成参数

Tab.2 GHH modified profile composition parameters

研究表明，增大计算程序中的型线离散点数，能减小与建模软件之间的误差[20]。本文针对GHH修正型线采用100、200、400、600等4种数量坐标点进行计算。由表4可知，随着坐标点的增大，程序计算的泄漏三角形面积与建模模型对比，其精度分别为94.28%、97.81%、99.35%、99.87%，其他特征参数变化较小，但是每组的计算时长相较于上一组，分别增加了14.81%、217.74%、208.51%。综合考虑计算精度和计算时长两者对计算的影响，本文采用400坐标点对型线的几何特征进行计算。

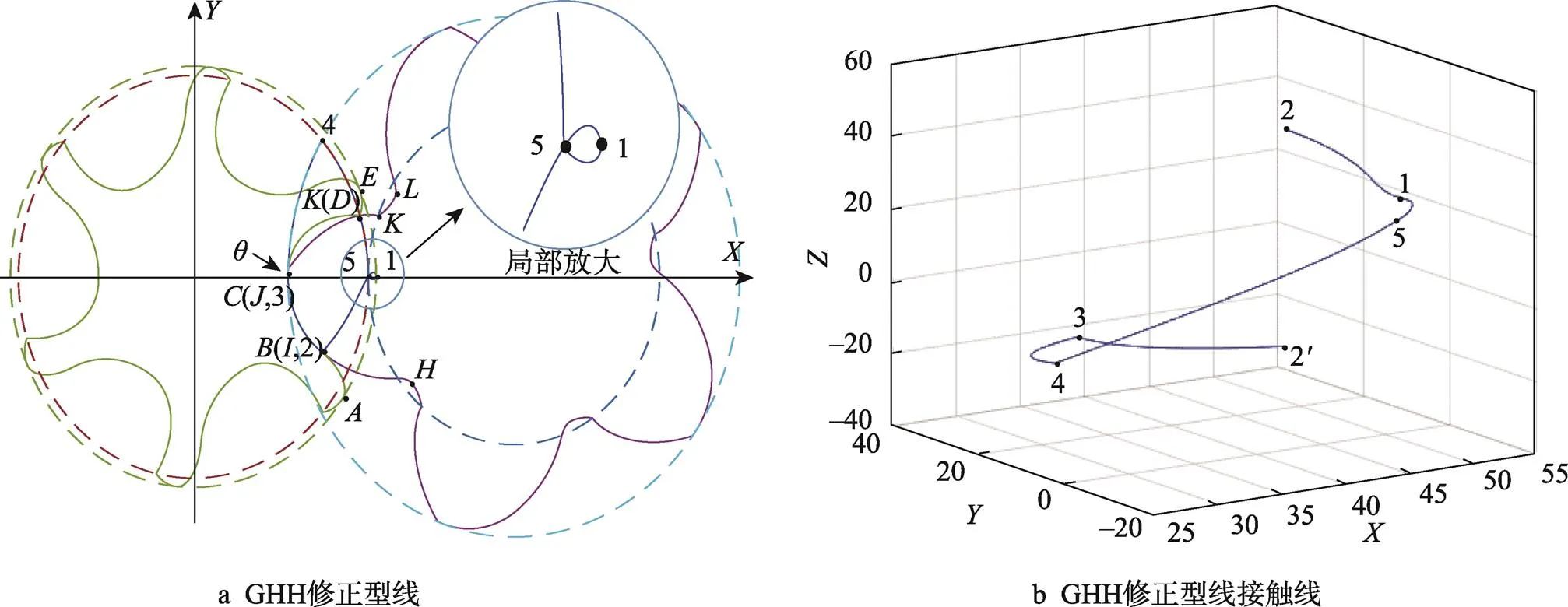
图3 GHH修正型线和接触线

表3 型线输入参数

Tab.3 Profile input parameter

表4 GHH修正型线离散点数无关性验证

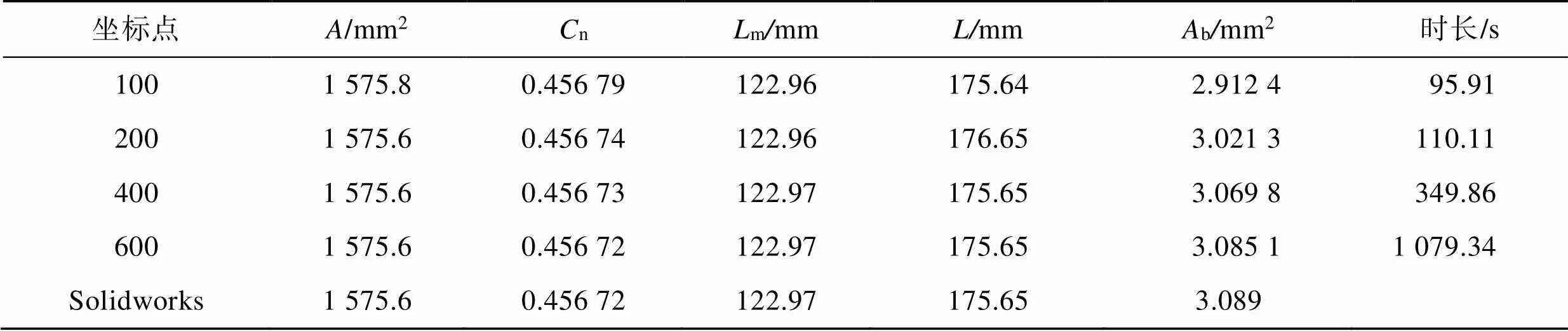
Tab.4 Verification of discrete point independence of GHH modified profile

1.4 几何特征对比

为了对比GHH和GHH修正型线转子几何特征的区别，采用表3中的型线初始设计参数，绘制了对应的螺杆转子。基于本文提出的几何特征计算方法，获得型线修正前后的几何特征，如表5所示，修正后的型线和n减小了0.006%，增大了0.30%，b不变，m减小了4.46%。如图4所示，修正后的型线在实现了啮合线封闭、长度减小的同时，对加工工艺的影响较小。

表5 型线几何特征

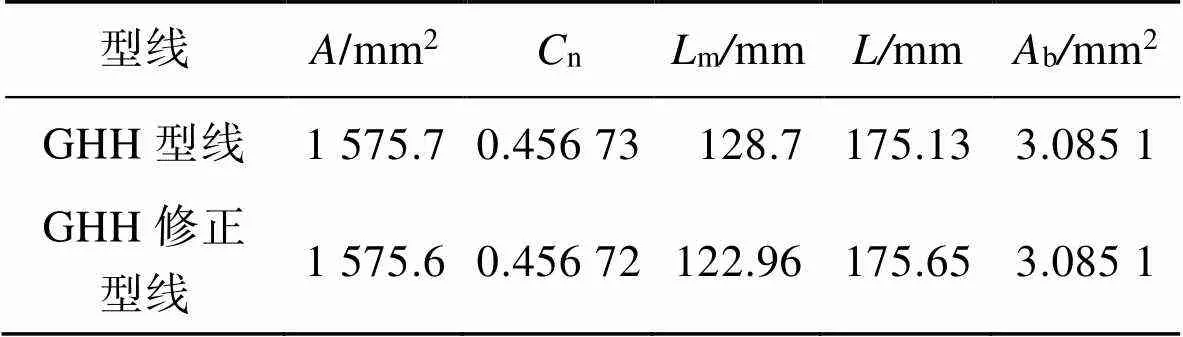
Tab.5 Geometric characteristics of profile

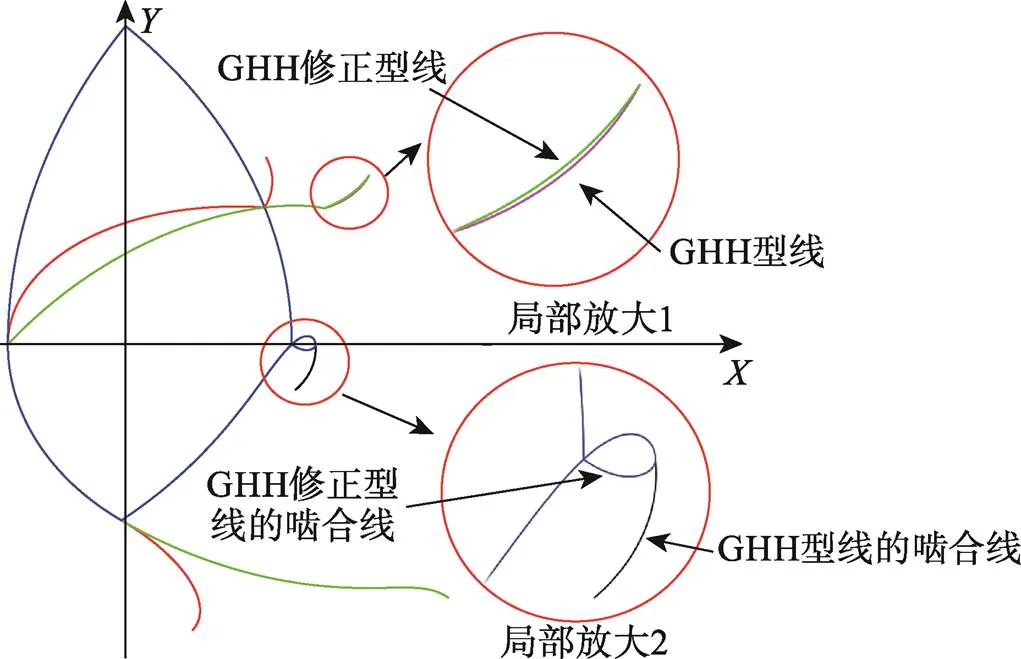
图4 GHH型线和GHH修正型线对比

1.5 计算方法

本文基于泄漏三角形等关键几何特征参数的计算方法，研究型线参数对螺杆压缩机几何特性的影响规律。首先建立型线绘制与几何特征计算数学模型；然后确定需要分析的自变量参数，计算并记录数据；最后分析自变量型线参数对因变量几何特征的影响规律，研究流程如图5所示。

2 结果与分析

本节研究4个关键设计参数，分别为阴转子节圆半径（p2）、阳转子内半径（i）、阴转子外半径（o）、导程（）对GHH修正型线齿间面积（）、面积利用率（n）、啮合线长度（m）、接触线长度（）、泄漏三角形面积（b）等几何特征的影响。

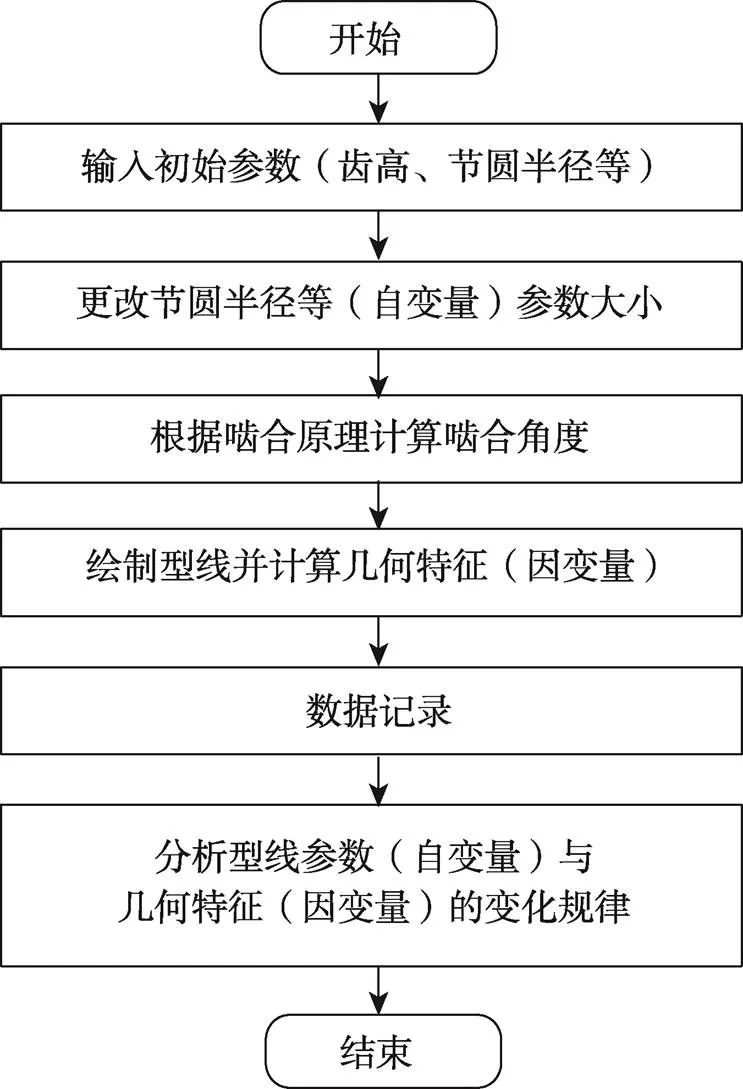
图5 GHH修正型线几何特征计算逻辑

2.1 节圆半径对型线几何特征的影响

如图6所示，随着节圆半径（p2）增大，阴、阳转子的尺寸增大，阴转子齿厚、阴阳转子中心距和阴转子节圆内啮合线增大，阴转子节圆外啮合线减小。

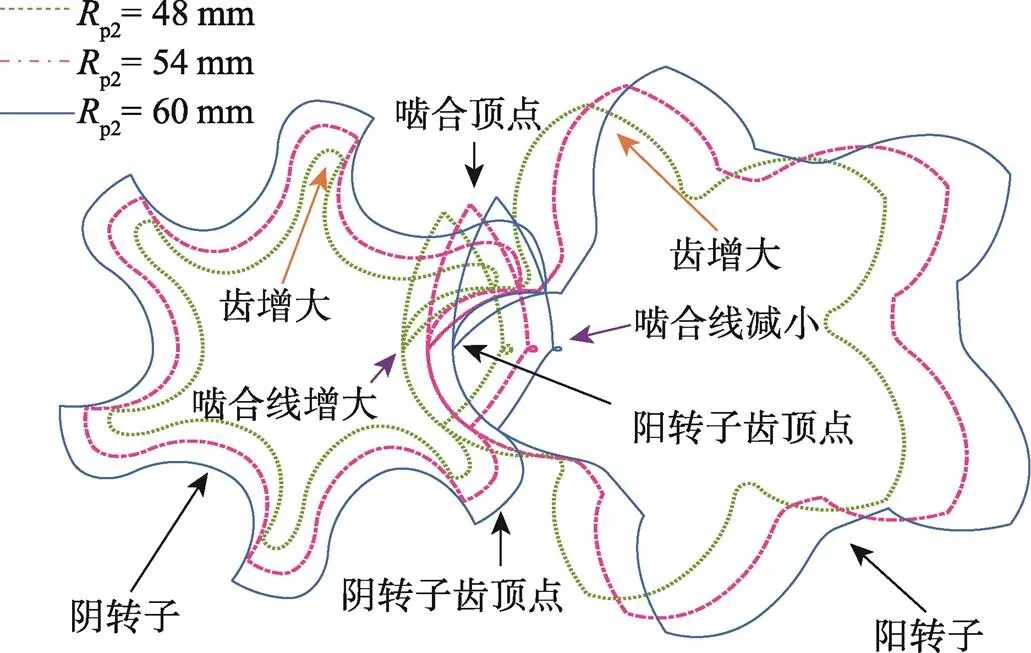
图6 不同阴转子节圆半径下的型线

如图7a所示，当节圆半径（p2）增大时，齿间面积（）增大，面积利用系数（n）减小。当p2分别为48、54、60 mm时，阳转子单齿面积（1）、阴转子单齿面积（2）和气缸端面面积（3）都随着p2的增大而增大，1分别为1 819.5、2 058.9、2 334 mm2，2分别为494.6、818.8、1 182.1 mm2和3分别为3 828.8、4 573、5 386.3 mm2。根据式（3）计算，齿间面积增大，其值分别为1 514.7、1 695.2、1 870.2 mm2。根据式（4）计算，面积利用率减小，其值分别为0.462、0.445、0.427。因此，可以通过减小p2来提高压缩机的容积效率。

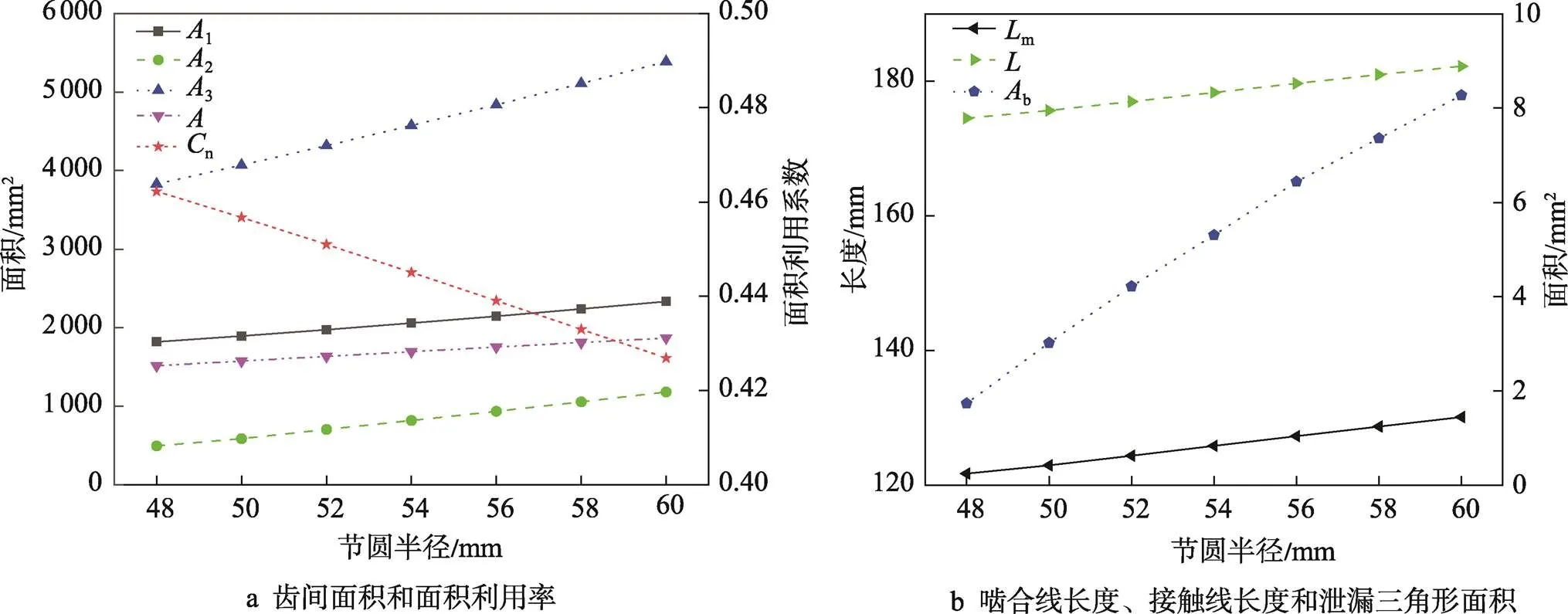
图7 不同阴转子节圆半径下的几何特征

如图7b所示，当节圆半径（p2）增大时，啮合线长度（m）增大，接触线长度（）增大，泄漏三角形面积（b）增大。如图6所示，当p2增大时，在阴转子节圆内侧的啮合线等比例放大，在阴转子节圆外的啮合线减小，但是啮合线在节圆外的减值远小于节圆内的增值，导致啮合线增大。接触线与啮合线保持相同变化规律。当p2增大时，啮合线顶点与机壳交点坐标间距变化很小，阴转子的齿顶点逐渐远离啮合顶点，使得阴转子的啮合顶点与齿顶点间的线段空间展开后与泄漏面延迟相交，增大了泄漏三角形的一条曲边长度，导致泄漏三角形面积大。但是随着泄漏三角形面积增大，增大量所占比重降低，导致增长速度放缓。

2.2 齿高对型线几何特征的影响

如图8所示，随着齿高（i）的增大，阴转子齿厚减小，阳转子齿厚、阴转子节圆内啮合线和阴转子节圆外啮合线均增大。

如图9a示，当齿高（i）增大时，齿间面积（）增大，面积利用系数（n）减小。当i分别为20、23、26 mm时，阳转子单齿面积（1）和气缸端面面积（3）随i的增大而增大，1分别为1 631.7、1 824、2 048.8 mm2，3分别3 749.3、3 987.3、4 236.7 mm2；阴转子单齿面积（2）随i的增大而减小，分别为813.8、655.4、477.7 mm2。根据式（3）计算，齿间面积随i的增大而增大，其值分别为1 303.8、1 507.9、1 710.1 mm2。根据式（4）计算，面积利用率随i的增大而增大，其值分别为0.429、0.450、0.469。因此，可以通过增大i来提高压缩机的容积效率。

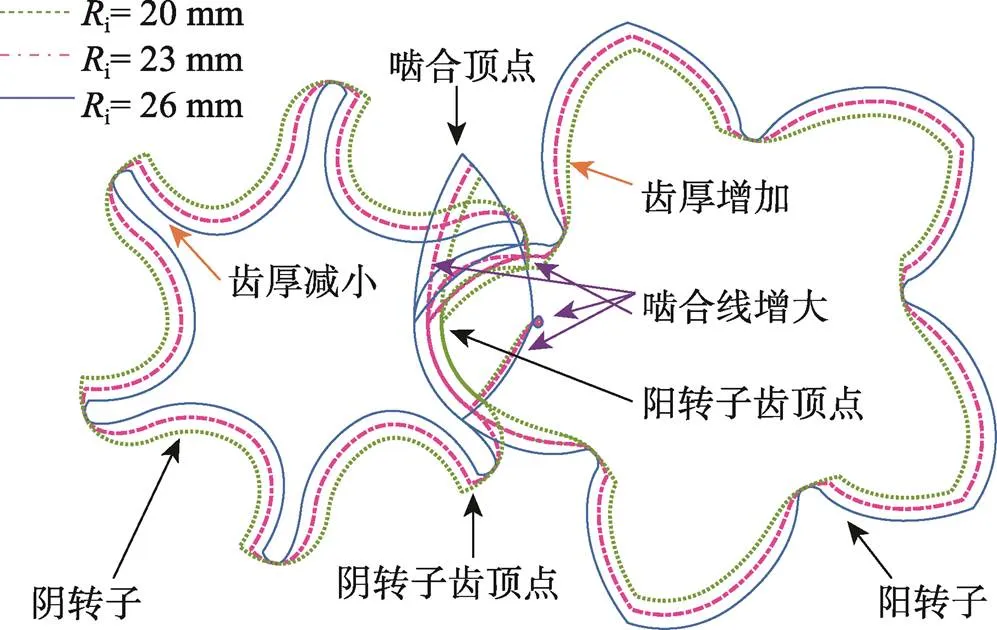
图8 不同齿高下的型线

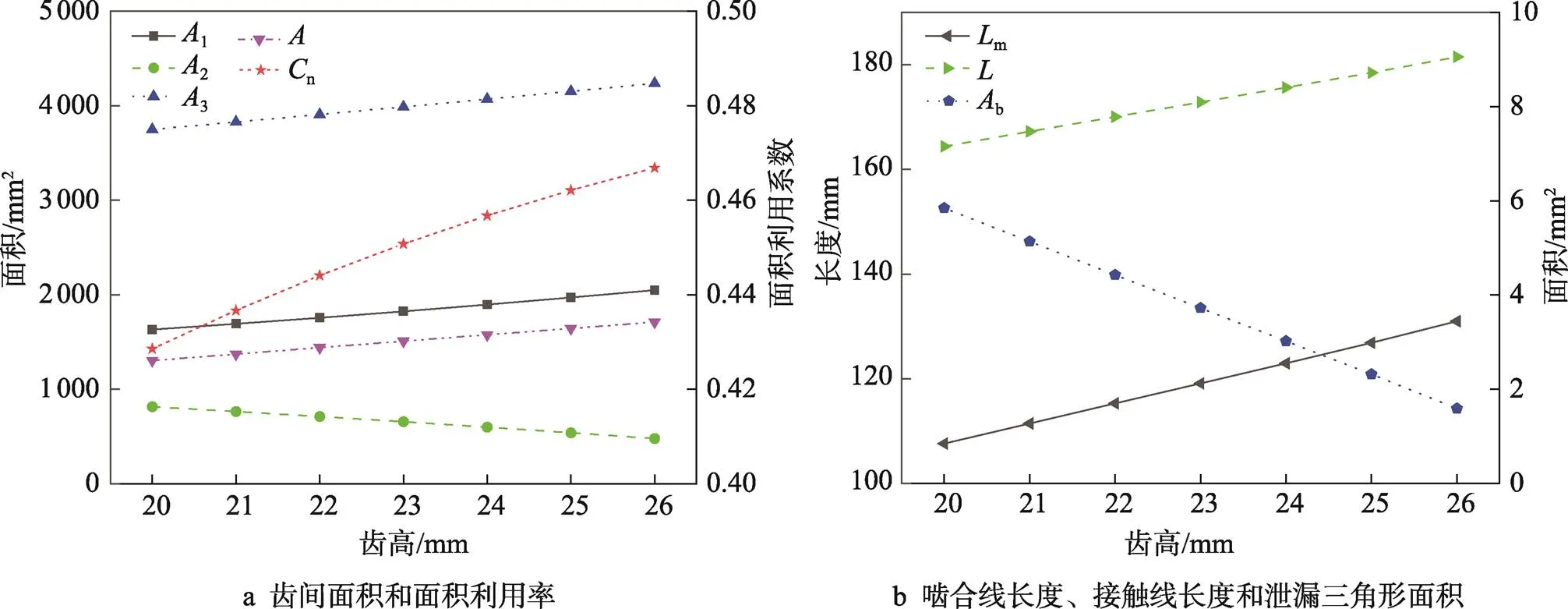
图9 不同齿高下的几何特征

如图9b所示，当齿高（i）增大时，啮合线长度（m）增大，接触线长度（）增大，泄漏三角形面积（b）减小。如图8所示，当i增大时，啮合线的顶端和底端均有所扩大，节圆内的部分可以看作等比放大，节圆外部分占啮合线整体比例较小，可忽略不计。空间接触线与啮合线保持相同变化规律。当i增大时，啮合顶点的位置向上运动，但阳转子所在的气缸半径增大，气缸交点也随之运动，两者之间的间距几乎不变，但是阴转子端的齿顶点与啮合顶点之间线段减小，使得阴转子的啮合顶点与齿顶点间的线段空间展开后与泄漏面提前相交，减小了泄漏三角形的一条曲边长度，最终导致泄漏三角形面积减小。

2.3 双边长度对型线几何特征的影响

如图10所示，随着双边长度（o）的增大，阳转子底部齿厚减小，阴转子顶部齿厚和阴转子节圆内外侧啮合线增大。

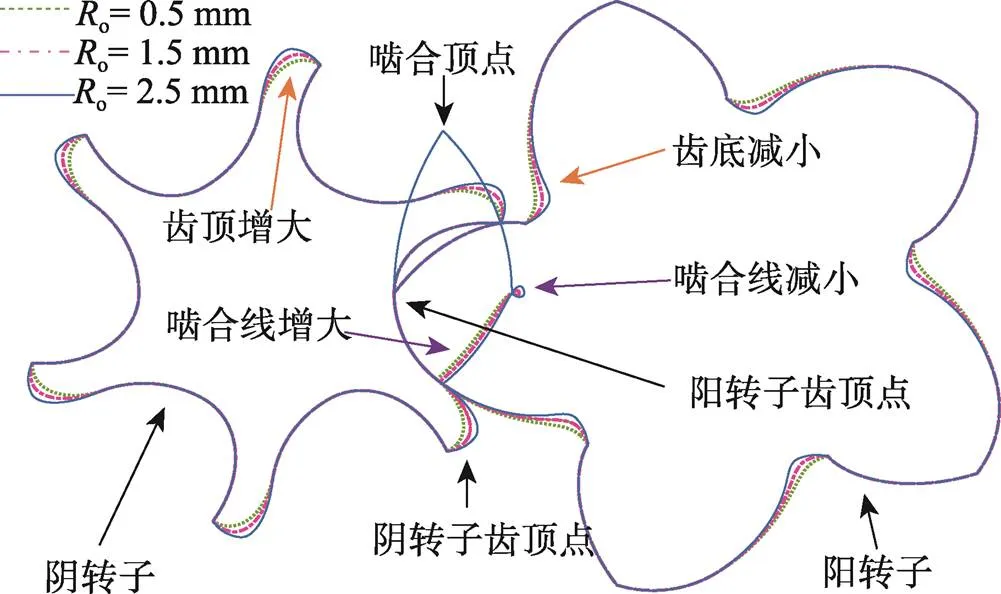
图10 不同双边长度下的型线

如图11a所示，当双边长度（o）增大时，齿间面积（）增大，面积利用系数（n）增大。当o分别为0.5、2、3.5 mm时，阳转子单齿面积（1）随o的增大而减小，分别为1 904.5、1 877.4、1 851.9 mm2，阴转子单齿面积（2）和气缸端面面积（3）随o的增大而增大，2分别为591.4、612.0、632.5 mm2，3分别为4 042.6、4 123.1、1 205.9 mm2。根据式（3）计算可得，齿间面积随o的增大而增大，其值分别为1 546.7、1 633.6、1 721.5 mm2。根据式（4）计算得出面积利用率增大，其值分别为0.448、0.474、0.499。由此可知o对转子容积性能的影响较小。

如图11b所示，双边长度（o）增大时，啮合线长度（m）增大，接触线长度（）增大，泄漏三角形面积（b）增大。如图10所示，当o增大时，啮合线位于节圆外部分增幅加大，导致啮合线长度增大。接触线与啮合线保持相同变化规律。当o增大时，阴阳转子的啮合线最高点虽然不发生变化，但是机壳交点位置会向上移动，使得其远离啮合线最高点，同时阴转子的齿顶点向着远离啮合线最高点方向运动，使得阴转子的啮合顶点与齿顶点间的线段空间展开后与泄漏面延迟相交，增大了泄漏三角形的一条曲边长度，两者相结合，造成泄漏三角形面积增大。

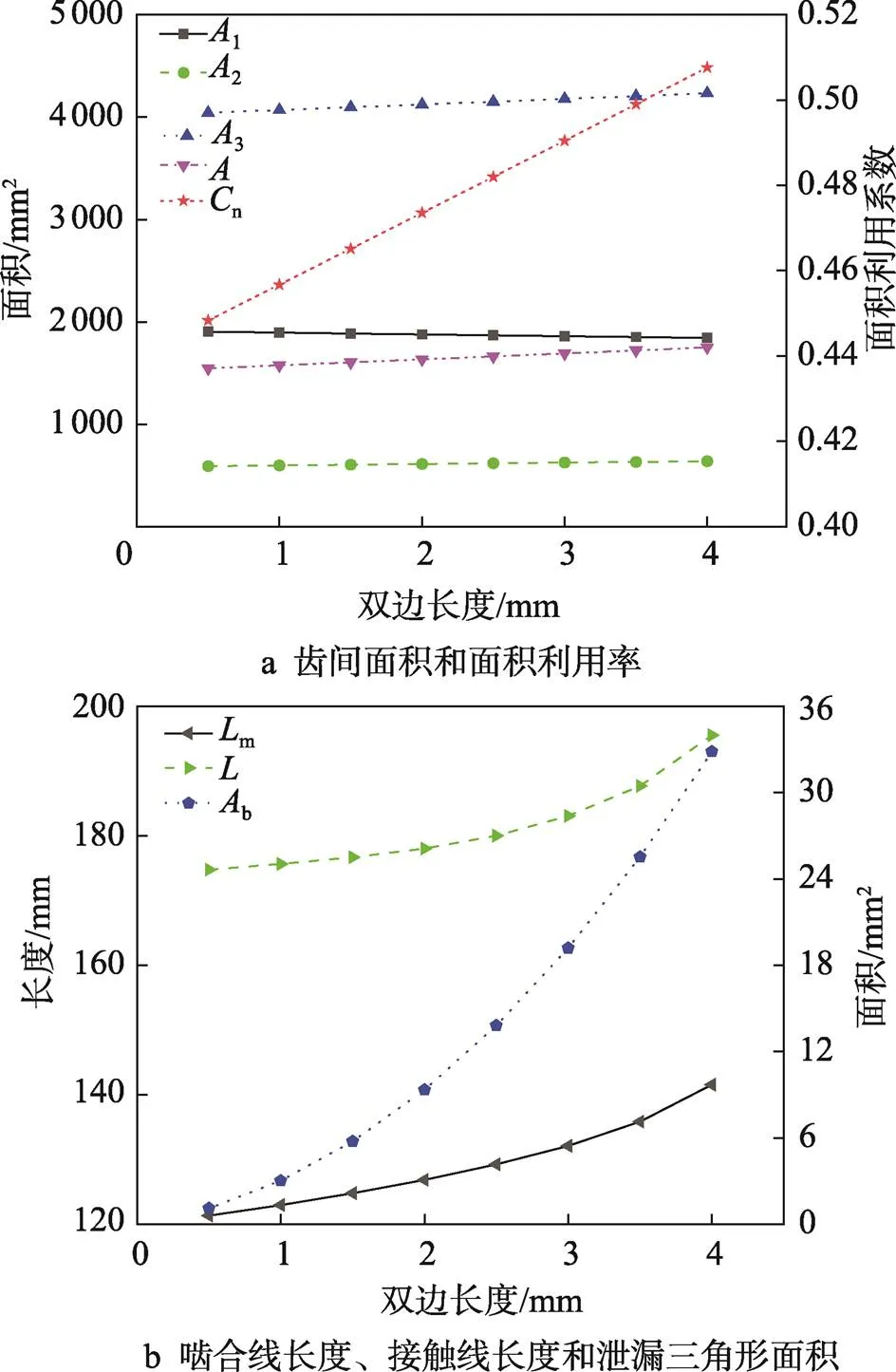
图11 不同双边长度下的几何特征

2.4 导程对型线几何特征的影响

如图12所示，随着导程（）的增大，转子端面的轮廓形状不变，3根曲线完全相同，导致其他2个型线组被完全覆盖。

如图13a所示，当导程（）增大时，齿间面积（）和面积利用率（n）均不发生改变。

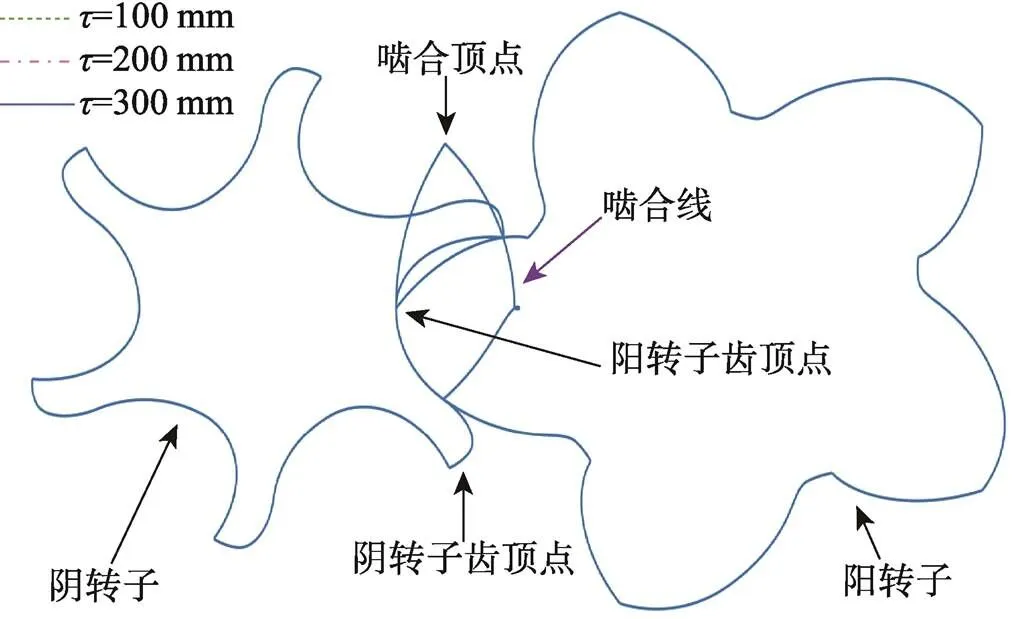
图12 不同导程下的型线

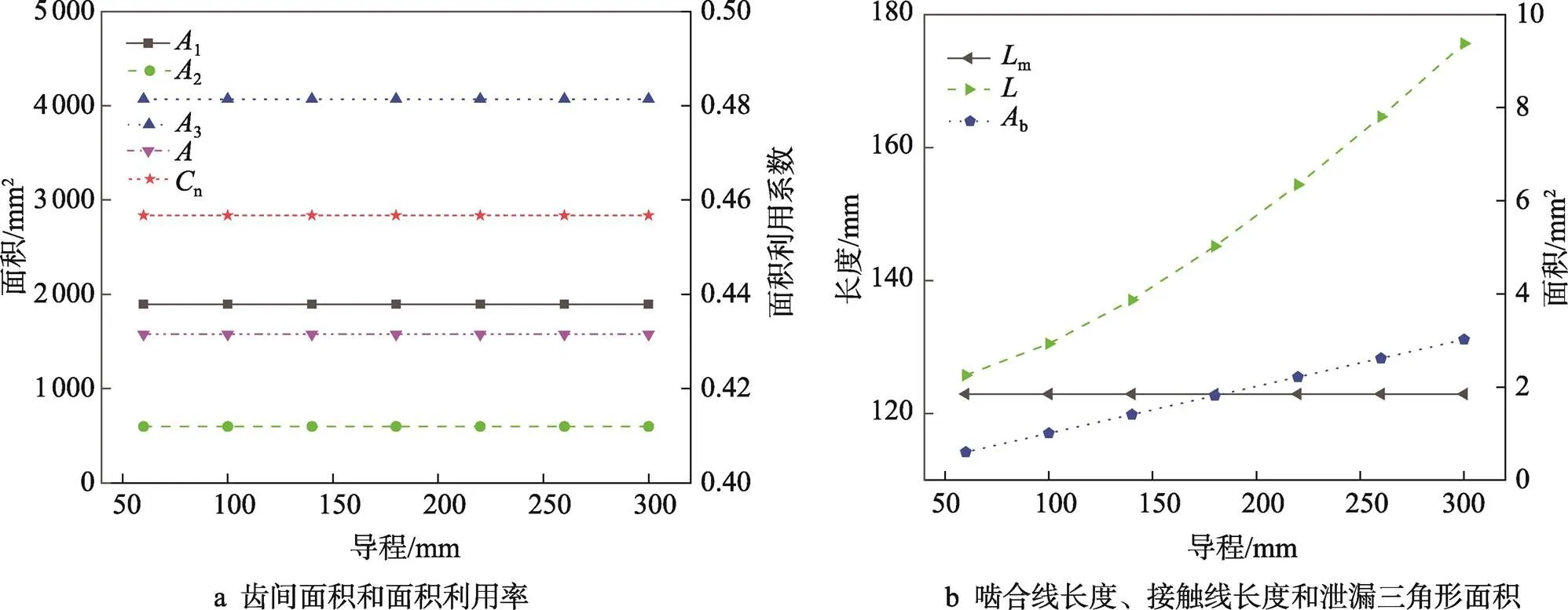
图13 不同导程下的几何特征

如图13b所示，当导程（）增大时，啮合线长度（m）保持不变，接触线长度（）增大，泄漏三角形面积（b）增大。当增大时，接触线每个坐标点对应的、值也会不变，因此啮合线不变。接触线每个坐标点对应的值也会增大，使得接触线长度增大。当增大时，阴、阳转子的齿顶点、啮合顶点、气缸交线、泄漏面均不发生变化，但会使2根泄漏三角形的曲线在空间上拉长，造成泄漏三角形面积的增大。

3 结语

本文针对大型冷库用螺杆压缩机转子设计与优化困难等问题，建立了双螺杆压缩机型线几何特征计算数学模型。基于该模型，分析了节圆半径、齿高等型线设计参数对泄漏三角形、接触线等几何特征的影响规律，为转子型线参数的选取提供了理论基础。具体结论如下：

1）提出了GHH修正型线，采用圆弧-圆弧包络型线替代GHH型线中的圆弧-圆弧型线，实现了型线接触线的连续，针对GHH修正型线进行参数化分析。

2）在螺杆压缩机容积性能方面，齿间面积随着节圆半径、齿高、双边长度的增大而增大，不受导程影响，其受齿高的影响最为明显。面积利用率随着齿高、双边长度的增大而增大，随节圆半径的增大而减小，不受导程影响，其受齿高的影响最为明显。

3）在螺杆压缩机密封性能方面，泄漏三角形随着节圆半径、导程的增大而增大，随齿高、双边长度的增大而减小，其受双边长度的影响最为明显。接触线长度随节圆半径、齿高、双边长度、导程的增大而增大，其受导程的影响最为明显。啮合线长度随节圆半径、双边长度的增大而增大，随齿高的增大而减小，与导程不相关，其受齿高的影响最为明显。

[1] 谢晶, 谭明堂, 杨大章, 等. 我国渔业仓储保鲜和冷链物流发展现状[J]. 包装工程, 2021, 42(11): 1-10.

XIE J, TAN M T, YANG D Z, et al. Development Status of Fisheries Storage-Preservation and Cold Chain Logistics in China[J]. Packaging Engineering, 2021, 42(11): 1-10.

[2] 孙锦涛, 游辉, 谢晶. 蓄冷板对冷库保温的影响实验[J]. 包装工程, 2022, 43(13): 107-116.

SUN J T, YOU H, XIE J. Experimental Research on Influence of Cold Storage Plate on Insulation of Cold Storage[J]. Packaging Engineering, 2022, 43(13): 107-116.

[3] 高青安. 长春市生鲜农产品冷链物流发展研究[D]. 长春: 吉林大学, 2021.

GAO Q A. Study on the Development of Cold Chain Logistics of Fresh Agricultural Products in Changchun City[D]. Changchun: Jilin University, 2021.

[4] CHEN W Q, WU X K, XING Z W, et al. Investigation of Characteristics of Discharge Pressure Pulsation in a Twin-Screw Refrigeration Compressor[J]. Archive Proceedings of the Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science, 2019, 233(6): 2206-2224.

[5] 黄艳, 章学来. 蓄冷技术在食品冷链物流中的研究进展[J]. 包装工程, 2015, 36(15): 23-29.

HUANG Y, ZHANG X L. Research Progress of the Application of Cold Storage Technology in Food Cold Chain Logistics[J]. Packaging Engineering, 2015, 36(15): 23-29.

[6] 韩美顺. 2020年度中国制冷设备市场分析[J]. 制冷技术, 2021, 41(S1): 67-86.

HAN M S. Analysis on Refrigeration Equipment Market of China in 2020[J]. Chinese Journal of Refrigeration Technology, 2021, 41(S1): 67-86.

[7] SCHRÖTER J, GRAF T, FRANK D, et al. Influence of Pressure Losses on Compressor Performance in a Pressurized Fuel Cell Air Supply System for Airplane Applications[J]. International Journal of Hydrogen Energy, 2021, 46(39): 21151-21159.

[8] TIAN Y F, GENG Y T, YUAN H, et al. Investigation on Water Injection Characteristics and Its Influence on the Performance of Twin-Screw Steam Compressor[J]. Energy, 2022, 259: 124886.

[9] HANJALIC K, STOSIC N. Development and Optimization of Screw Machines with a Simulation Model 1 Profile Generation[J]. Journal of Fluids Engineering, 1997, 119(3): 659-663.

[10] STOSIC S, SMITH I, KOVACEVIC K, et al. Geometry of Screw Compressor Rotors and Their Tools[J]. Journal of Zhejiang University-Science A (Applied Physics & Engineering), 2011, 12(4): 310-326.

[11] 朱俊杰, 屈宗长, 冯健美. 新型锥形双螺杆压缩机的结构和原理[J]. 流体机械, 2007, 35(8): 22-24.

ZHU J J, QU Z C, FENG J M. Structure and Theory for a Taper Twin Screw Compressor[J]. Fluid Machinery, 2007, 35(8): 22-24.

[12] 张炯焱. 双螺杆压缩机齿型优化[J]. 压缩机技术, 2020(2): 49-53.

ZHANG J Y. Optimization of the Twin Screw Compressor Rotor Structure[J]. Compressor Technology, 2020(2): 49-53.

[13] 李雪琴, 沙润东, 李宏鑫, 等. 双螺杆真空泵的新型椭圆弧型螺杆转子研究[J]. 真空科学与技术学报, 2021, 41(1): 64-68.

LI X Q, SHA R D, LI H X, et al. Novel Type of Elliptical Arc Rotor of Twin-Screw Vacuum Pump: An Analytical Study[J]. Chinese Journal of Vacuum Science and Technology, 2021, 41(1): 64-68.

[14] BYEON S S, LEE J Y, KIM Y J. Performance Characteristics of a 4×6 Oil-Free Twin-Screw Compressor[J]. Energies, 2017, 10(7): 945.

[15] BUCKNEY D, KOVACEVIC A, STOSIC N. Rotor Clearance Design and Evaluation for an Oil Injected Twin Screw Compressor[J]. British Food Journal, 2015, 90(1): 12003.

[16] HE Z, WANG T, WANG X, et al. Experimental Investigation into the Effect of Oil Injection on the Performance of a Variable Speed Twin-Screw Compressor[J]. Energies, 2018, 11(6): 1342.

[17] WANG J, ZHAO X H, ZHAO L Z, et al. Clearance Distribution Design and Thermal Deformation Analysis of Variable-Pitch Screw Rotors for Twin-Screw Vacuum Pumps[J]. Vacuum, 2023, 211: 111936.

[18] WANG J, ZHAO L Z, ZHAO X H, et al. Optimal Design and Development of Two-Segment Variable-Pitch Screw Rotors for Twin-Screw Vacuum Pumps[J]. Vacuum, 2022, 203: 111254.

[19] FLEMING J S, TANG Y, COOK G. The Twin Helical Screw Compressor Part 1: Development, Applications and Competitive Position[J]. Archive Proceedings of the Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science, 1998, 212(5): 355-367.

[20] 王涛, 齐强, 何志龙, 等. 螺杆压缩机泄漏三角形面积变化规律[J]. 流体机械, 2023, 51(2): 70-77.

WANG T, QI Q, HE Z L, et al. Change Law of Blow Hole Area of Screw Compressor[J]. Fluid Machinery, 2023, 51(2): 70-77.

Geometric Characteristics and Profile Optimization of Screw Compressor in Large Cold Storage

WANG Tao1,2, QI Qiang1, DONG Yan3, ZHANG Dehai1, CAI Yingjun2*, ZHAN Dengyi1

(1. Zhengzhou University of Light Industry, Zhengzhou 450002, China; 2. Institute of Process Engineering, Chinese Academy of Sciences, Beijing 100190, China; 3. Institute of Urban Safety and Environmetal Science, Beijing Academy of Science and technology, Beijing 100054, China)

The work aims to establish a mathematical model for calculating the profile and geometric characteristics specific to the profile design and optimization of screw compressor in large cold storage system, so as to provide theoretical basis for the profile design and optimization of screw compressor. With the widely used GHH profile as the research object, based on the geometric characteristic calculation method adopted, it was found that the sealing line of GHH profile was discontinuous. By replacing the arc-arc conjugate curve pair in the GHH profile with the arc-arc envelope conjugate curve pair, the continuity of the sealing line was achieved, and a modified GHH profile was proposed. Taking the modified GHH profile as the research object, the effect of profile parameters such as pitch radius of female rotor, inner radius of the male rotor and outer radius of the female rotor on the geometric characteristics of contact line, the meshing line and the blow hole was analyzed. The blow hole area was linearly positively correlated with the pitch radius of female rotor, the screw lead and the protection angle, and linearly negatively correlated with the inner radius of the male rotor and the outer radius of the female rotor and the radius of the elliptic arc. The outer radius of the female rotor had the greatest effect on the area of the blow hole. The area utilization rate decreased from 0.462 to 0.427, the length of the sealing line elevated from 174.5 to 182.3 mm and the blow hole area enlarged from 1.7 to 8.3 mm2when the pitch radius of the female rotor increased from 48 to 60 mm. The established mathematical model for rapid calculation of geometric characteristics of rotor profile optimizes GHH profile, reduces leakage during rotor operation, improves theoretical Engine displacement, and provides theoretical guidance for rotor profile optimization.

screw compressor; contact line; meshing line; blow hole; GHH profile

TB486；TB65；F766

A

1001-3563(2024)01-0019-09

10.19554/j.cnki.1001-3563.2024.01.003

2023-08-08

国家自然科学基金（52006201）