磁脱扣器动作响应分析及储能电容匹配设计

李 奎，佟 盟，武 一，卢志伟，胡博凯，徐子健

（1.河北工业大学 河北省电磁场与电器可靠性重点实验室，天津 300401；2.河北工业大学 省部共建电工装备可靠性与智能化国家重点实验室，天津 300401）

0 引言

随着电力行业的高速发展，因漏电引起的火灾和触电事故隐患问题越来越突出，当发生漏电事故时，漏电保护器能快速切断电源，有效保护人身和电气设备安全［1］。电磁式漏电保护器结构简单，无需辅助电源，工作过程中不依赖电网电压而被广泛使用［2-3］。磁脱扣器是电磁式漏电保护器核心组件，而抗扰型漏电保护器中，储能电容与脱扣线圈作为连接驱动电路与磁脱扣器的纽带，合理的设计是保证漏电保护器可靠工作的关键。

磁脱扣器是一种典型的电磁元件，随着虚拟样机技术的发展，很多学者对其及此类元件进行了深入研究［4-7］。有学者分析了干扰磁场对磁脱扣器的影响，并且对其磁路结构和屏蔽罩进行优化，提高了磁脱扣器的抗干扰能力［8-10］。纽春萍等建立了接触器电磁系统数学模型并借助ADAMS 实现对接触器在机械力与弹簧力作用下动态特性的分析［11］；ZHU Tiansheng 等通过ANSYS 有限元仿真研究了分励脱扣器电磁系统，并应用随机遗传算法对其结构进行了优化［12］；ATIENZA E 等应用FLUX2D 对磁保持式脱扣器衔铁气隙与电磁力进行计算，并通过PASCOSMA 与MATHCAD 进行结构优化，降低了动作时间与器件耗材［13］。目前，对电磁开关的研究手段主要分为磁路分析法与有限元磁场分析法［14］。等效磁路法计算速度较快，但精度较低，主要用于对磁路影响因素进行分析；有限元磁场计算速度较慢，但能获得较高精度，能对电磁系统的磁场分布进行精确求解。在有限元分析计算中，传统的衔铁动作特性计算方法是通过建立有关气隙与电流的电磁力二维表格［15］，并在动力学模型中对衔铁位移进行求解，这种方法耗时较长且精度不高，不能实时反映机构动态特性，因此有学者提出了耦合电路、磁场与衔铁运动的动态模型，能够实时计算各电磁量与力学量在机构衔铁运动中的相关关系［16］。

在漏电保护技术方面，有许多学者对电子式漏电保护器的设计进行了研究。吴茂提出一种基于PIC 单片机技术的智能型漏电保护器的设计，提升了漏电保护器的可靠性和抗干扰性［17］。洪传生等优化了驱动电路稳压设计，提高了漏电保护器抗干扰能力［18］。王尧等提出一种抗电快速瞬变脉冲群的漏电保护器综合设计方法［19］。抗扰型电磁式漏电保护器中，电容储能直接影响漏电保护器的漏电保护动作时间，而储能值过低无法驱动磁脱扣器［20］。一般情况下为保障磁脱扣器可靠动作，电容储能需要足够大，造成漏电保护时间较长。因此，本文围绕影响磁脱扣器可靠脱扣的影响因素进行分析，研究衔铁可靠释放的临界条件，确定最佳匹配电容，降低衔铁释放所需电容储能，从而缩短漏电保护动作时间，为实现电磁式漏电保护器的快速动作奠定基础。

1 磁脱扣器工作原理

电磁式漏电保护器一般是由剩余电流互感器（residual current transformer，RCT）、驱动电路、磁脱扣器构成，如附录A 图A1所示。磁脱扣器为核心动作构件，由磁轭、衔铁、永磁体、反力弹簧等组成，在正常情况下由永磁磁动势提供的磁吸力矩Me大于弹簧反力矩Ms，使衔铁保持闭合。剩余电流经RCT将一次侧电流转化为二次侧电压并施加到驱动电路上，在脱扣线圈中产生去磁磁势。当主线路剩余电流IΔ大于最小动作值时，衔铁与磁轭接触面间的磁吸力矩小于弹簧反力矩，磁脱扣器动作，触发漏电保护器脱扣机构，切断主回路，实现对线路漏电的保护。

驱动电路分为快速动作型驱动电路与抗扰驱动电路，如图1 所示。快速动作型驱动电路中，二极管D1与D2起限压作用；C1与C2为补偿电容，漏电信号经RCT、驱动电路直接输出至脱扣线圈LR，在正常工况下能够在较短的时间内驱动脱扣器动作，但抗干扰能力较弱。抗扰型驱动电路中，R1与C3分别为补偿电阻与补偿电容；D3— D6构成整流桥，C4为储能电容，R2为电阻，D7为续流二极管，漏电信号经剩余电流互感器对储能电容进行充电，当储能电容两端电压到达检测芯片的触发电压时，晶体管Q1导通，电路由充电状态进入储能释放状态，并驱动磁脱扣器，其抗干扰能力强。

图1 漏电保护器工作电路图Fig.1 Circuit diagram of residual current device

对于抗扰型驱动电路，当线路流过强浪涌脉冲时，储能电容两端电压不会立刻上升至触发电压，可以避免误脱扣，但动作时间相对较长。因此需要对储能电容与磁脱扣器进行匹配设计，在保证可靠驱动磁脱扣器的前提下尽量缩短储能电容充电时间，实现抗扰型电磁式漏电保护器快速动作的目的。

2 不同激励源下磁脱扣器衔铁释放响应状态分析

2.1 恒压激励源下磁脱扣器衔铁释放响应状态

磁脱扣器线圈是阻感负载，对于感性回路，激励时间在4 倍时间常数以上，其电流就能达到稳态值，此时可认为电源为恒压激励源。脱扣线圈两端电压u可表示为：

式中：L为线圈等效电感；α为衔铁角位移；α′为衔铁角速度；i为线圈电流，R为线圈电阻。

根据磁脱扣器实际尺寸建立仿真模型，包括衔铁、磁轭和永磁体，衔铁与磁轭材料为1J50 坡莫合金，永磁体为铝镍钴，主要参数如附录A 表A1所示，磁脱扣器等效磁路与有限元计算模型如附录A 图A2所示。

衔铁所受磁力矩Me为脱扣线圈所提供的电磁力矩与永磁力矩的合力矩，如式（2）所示。

式中：Hmlm为永磁体磁动势；iN为脱扣线圈磁动势；Rm为永磁体内磁组；R0为永磁体到磁轭间等效气隙磁阻；R1为磁路支路磁阻；R2为磁轭与衔铁磁阻；Rδ1与Rδ2为衔铁与磁轭间两接触面气隙磁阻。

根据磁力矩Me和弹簧反力矩Ms可由式（3）计算衔铁角动量与角位移：

式中：t0为激磁安匝上升至阈值安匝时刻。

磁力矩与弹簧力矩相等时的激磁安匝为阈值安匝i0N，当磁力矩为0 时，表示线圈激磁安匝完全抵消永磁体的磁通，该激磁安匝为imN。根据激励电压幅值，可以计算出稳态下的激磁安匝，并通过三维有限元模型，计算出衔铁所受力矩，如附录A 图A3所示，衔铁有3种响应情况：

1）激励幅值小于阈值电压，激磁安匝小于阈值安匝，磁力矩大于弹簧力矩，衔铁保持闭合状态；

2）激励幅值等于阈值电压，激磁安匝稳态值等于阈值安匝，磁力矩等于弹簧力矩，衔铁处于临界释放状态；

3）激励幅值大于阈值电压，激磁安匝稳态值大于阈值安匝，磁力矩小于弹簧力矩，衔铁可靠释放。

因此恒压激励下衔铁可靠释放的条件是：激励电源电压幅值高于阈值电压，使线圈稳态激磁安匝大于阈值安匝，衔铁磁吸力矩小于弹簧反力矩。

2.2 脉冲激励源下磁脱扣器衔铁释放响应状态

2.2.1 磁脱扣器衔铁响应状态分析

在脉冲激励源下，衔铁在激励源消失后应具有足够的角动量，才能可靠释放。若脉冲激励源持续时间短，则衔铁分离一段距离后，在永磁体磁场作用下，衔铁重新闭合，不能释放。其变化情况如下。

1）脉冲幅值小于阈值电压，激磁安匝小于阈值安匝i0N，磁力矩大于弹簧力矩，衔铁保持吸合状态，如图2（a）所示。

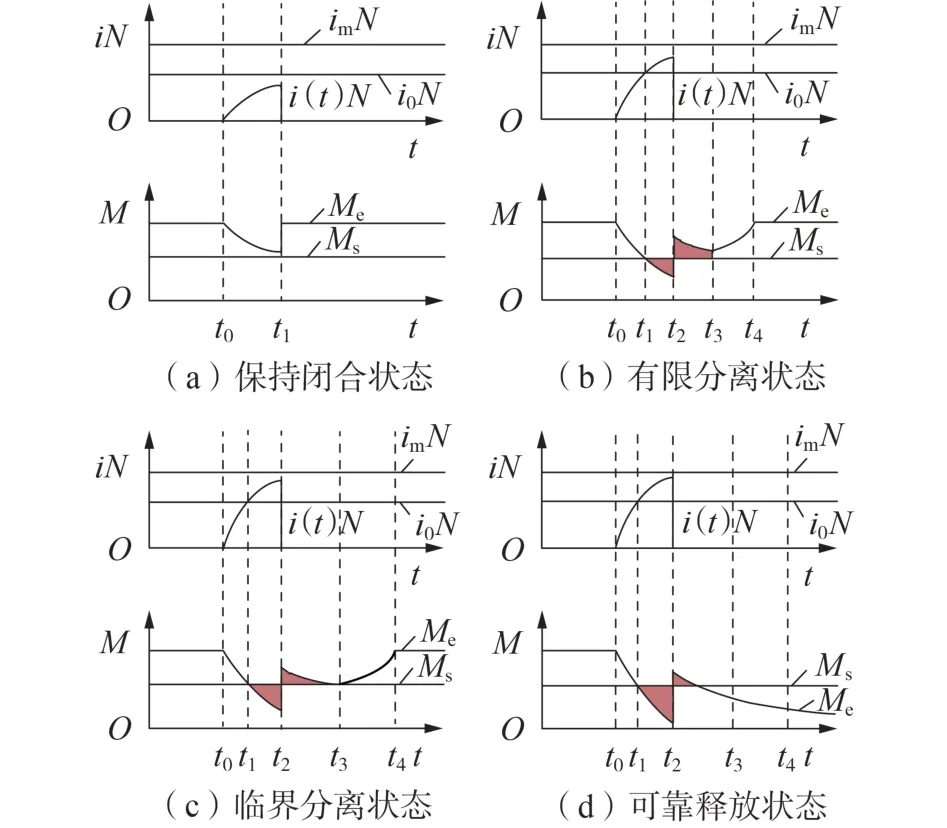
图2 不同脉冲激励源下力矩变化示意图Fig.2 Diagram of torque with different excitation

2）脉冲幅值或脉冲宽度增加，激磁安匝大于阈值安匝i0N，衔铁开始分离。脉冲电源结束后，其角动量为零时角位移最大。若此时磁力矩大于弹簧力矩，则衔铁重新闭合。将此种状态称为衔铁有限分离状态，如图2（b）所示。

3）脉冲幅值或脉冲宽度增加到一定值，衔铁打开气隙使永磁力矩与弹簧力矩平衡时，其角动量为零，将此状态称为衔铁临界分离状态，如图2（c）所示。

4）脉冲幅值或脉冲宽度继续增加，则激磁安匝继续增大，衔铁在受力平衡的气隙位置时仍有一定的角动量，则永磁吸力矩不能使衔铁恢复闭合，此种状态称为衔铁可靠释放状态，如图2（d）所示。

2.2.2 磁脱扣器衔铁释放响应状态仿真

根据式（3）与式（4），可以确定衔铁的运动状态。在表A1所示的参数下进行有限元仿真计算，激励为200 mV、脉冲宽度tw≤ 6 ms 时，衔铁保持闭合；6 ms ＜tw＜9 ms 时，衔铁有限分离；tw= 9 ms 时，衔铁临界分离；tw＞9 ms时，衔铁可靠释放，具体如图3所示，其与图2理论分析结果相符。

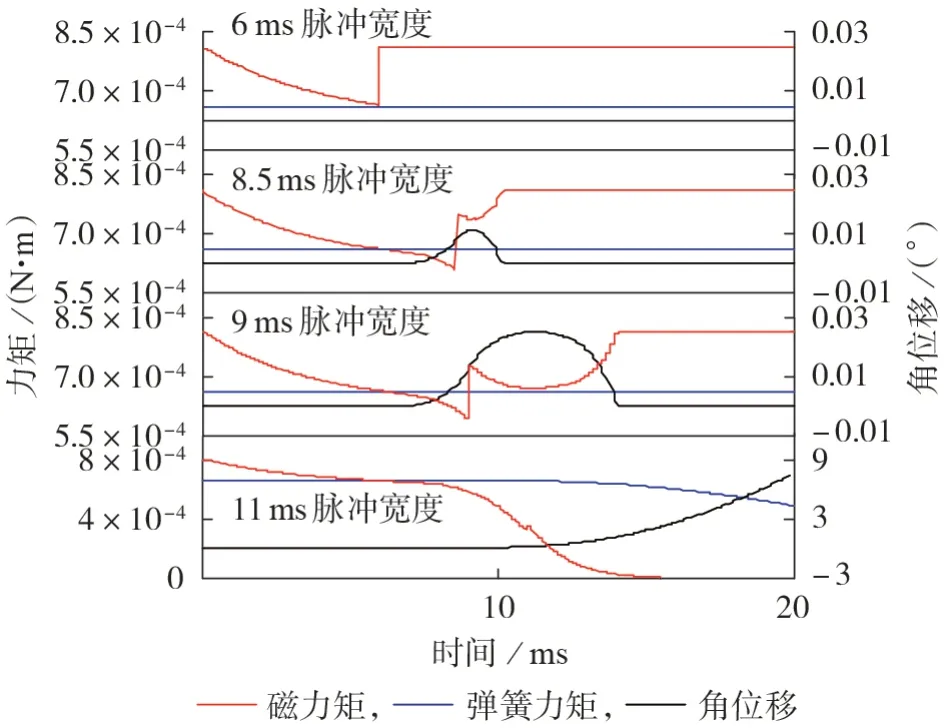
图3 不同脉冲宽度衔铁力矩与角位移曲线Fig.3 Torque and angular displacement curves with different pulse widths

从图3 可以看出衔铁在不同脉冲宽度下的4 种响应，分别为保持闭合、有限分离、临界分离和可靠释放，在临界分离时最大角位移约为0.026°，此时磁力矩与弹簧力矩平衡。

在180、200、220 mV 下进行磁脱扣器衔铁所受磁力矩和角位移的仿真分析，衔铁临界分离下其变化规律见附录A 图A4。由仿真结果可见，不同脉冲电压源激励下衔铁临界分离时的最大角位移为恒定值，即磁力矩与弹簧力矩相等的平衡位置。180、200、220 mV 下衔铁达到临界分离状态时所受磁力矩最小值分别为6.69×10-4、6.68×10-4、6.71×10-4N·m，接近弹簧力矩理论值6.61×10-4N·m，误差在5.7 %以内。

2.2.3 磁脱扣器衔铁临界分离状态分析

在脉冲激励电源消失后，衔铁状态取决于衔铁角位移及此位置下的角动量。衔铁在某角位移下，其角动量小于一定值，则衔铁重新闭合，而大于该值，衔铁能够可靠释放，该值称为衔铁临界角动量。一般情况下，衔铁临界分离状态下角位移很小，永磁力矩近似线性变化，仿真结果如附录A图A5所示。

衔铁所受力矩可表示为：

式中：Mpe为永磁力矩；M0为衔铁吸合位置时永磁力矩与弹簧力矩差值；α0为衔铁受力平衡时角位移，在该角位移下衔铁角动量为零时也可以释放。

由转动动能定理可得：

联立式（5）与式（6）可得衔铁临界角动量为：

由式（7）可知，在不同角位移下衔铁临界角动量线性变化。

当激磁安匝上升至阈值安匝i0N时，衔铁开始释放，随着激磁安匝继续增加，磁力矩继续减小，衔铁角动量与角位移增大。若激励截止后，衔铁最大角动量等于临界角动量，则衔铁在永磁吸力矩的作用下角动量逐渐减小，角位移继续增加，一段时间后衔铁运动至最大角位移α0，衔铁处于临界分离状态。仿真计算不同脉冲激励下接近临界分离时衔铁角动量变化，其轨迹如附录A 图A6 所示，图中虚线为临界角动量。从图中衔铁角动量变化轨迹可以看出，衔铁最大角位移略小于临界状态理论平衡位置，衔铁接近受力平衡位置时，其所受磁力矩大于弹簧力矩，因此衔铁将恢复闭合。若激励电压幅值或脉冲宽度略微增加，衔铁将可靠释放。同时，图A6与图3（c）所示结果一致。

综上所述，衔铁可靠释放需要脉冲激励电压超过一定值，且脉冲宽度也需达到一定值。因此，在脉冲激励下衔铁释放条件为：衔铁最大角动量超过临界角动量，达到力矩平衡位置时角动量大于0。

2.3 电容电压激励源下磁脱扣器衔铁释放响状态

由图2 可知，抗扰型电磁式漏电保护器是通过电容储能驱动磁脱扣器的，当储能电容两端电压达到电压检测芯片触发阈值后，电容电压施加到磁脱扣器上，可将其分为储能释放阶段和续流阶段2 个工作阶段。储能开始释放后，电容两端电压逐渐降低，激磁安匝逐渐增加至峰值。当电容电压降为0时其储能完全释放，电路进入续流工作状态，直至激磁安匝降为0。简化后的电路工作过程如图4所示。

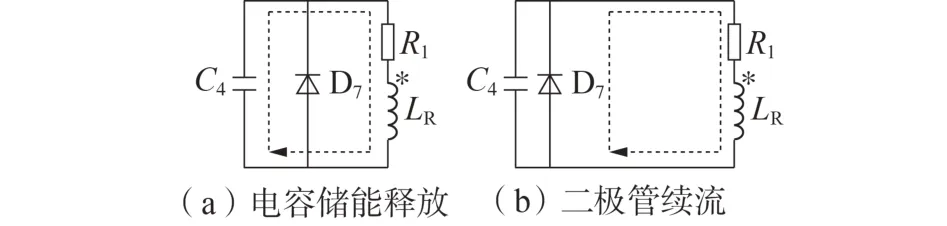
图4 储能释放过程示意图Fig.4 Schematic diagram of energy storage release process

在电容储能完全释放前，电路可简化为RLC 回路，电容电压uc可表示为：

式中：C为储能电容容值。

一般情况下储能电容较小，电路工作在欠阻尼下，此时电容电压uc与激磁安匝ic(t)N分别为：

忽略二极管管压降，电路工作在续流阶段时的激磁安匝可表示为：

式中：t0为续流起始时刻。

在电容电压激励源下，磁脱扣器线圈激磁安匝波形如附录A 图A7 所示。当激磁安匝上升到阈值安匝i0N时衔铁开始释放。随着激磁安匝继续上升，磁吸力矩继续下降，衔铁角动量与角位移增大。但超过一定时间后，激磁安匝开始下降，衔铁所受磁力矩随之增加。由于衔铁具有一定的角动量，衔铁仍会继续释放。若衔铁达到平衡位置时角动量大于零，则衔铁能够可靠释放。

在电容电压激励源下进行衔铁响应状态的仿真分析，在储能电容272 nF 下，衔铁所受电磁力矩、弹簧力矩和角位移的有限元仿真结果如图5所示。

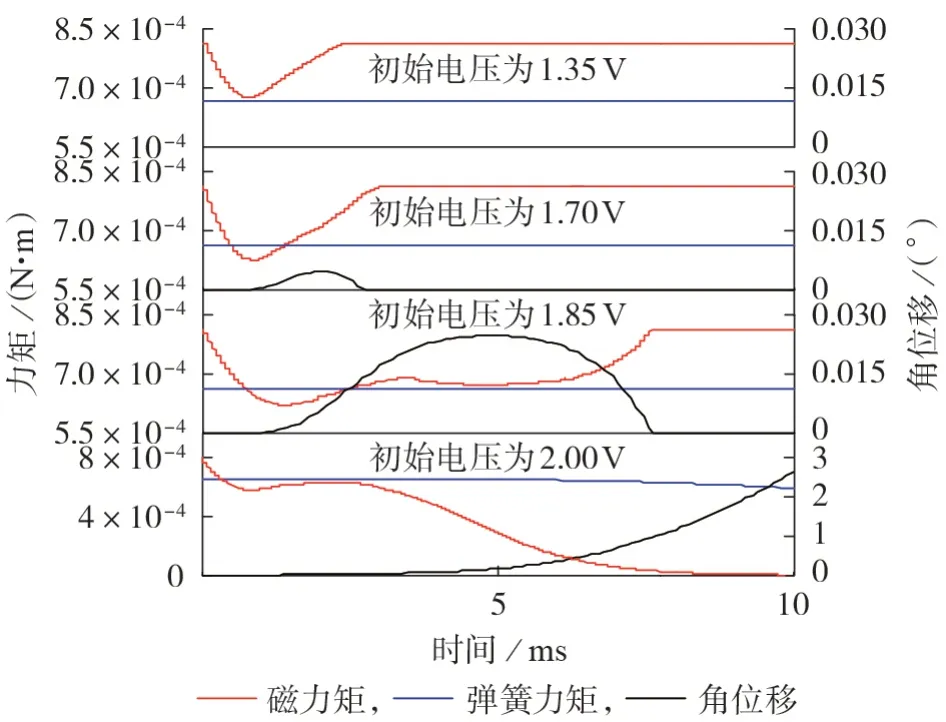
图5 不同初始电压下衔铁运动曲线Fig.5 Coil ampere turns and armature release motion curves with different initial voltages

仿真结果表明：电容初始电压U0≤1.35 V 时，衔铁保持闭合；1.35 V＜U0＜1.85 V 时，衔铁有限分离；U0=1.85 V时，衔铁临界分离；U0＞1.85 V时，衔铁可靠释放。

衔铁释放过程中角动量与角位移仍可由式（3）与式（4）计算，和脉冲电源激励下不同，电容电压激励下激磁安匝下降至阈值安匝，衔铁角动量峰值低于临界角动量，由于脱扣线圈激磁安匝不为0，其角动量下降速度减小，在激磁安匝为0 时衔铁角动量仍能达到临界角动量。在不同电容和电压下进行衔铁角动量的仿真计算，临界条件下衔铁角动量变化轨迹如附录A 图A8 所示，其与图A6 中的变化轨迹有显著差异。

因此，在电容电压激励下衔铁可靠释放条件为：激磁安匝为0 时衔铁角动量超过临界角动量，其在受力平衡位置角动量应大于0。

3 储能电容匹配设计

在电容电压激励源下，电容容值不同，其储能释放过程不同，对衔铁释放运动过程影响不同。由式（10）与式（11）可知，若电容储能值一定，电容增大，则电压降低，虽然激磁安匝脉冲宽度增加，但激磁安匝幅值降低。当储能电容电压降低到一定程度时，激磁安匝峰值小于衔铁释放阈值，弹簧反力矩一直小于磁吸力矩，因此衔铁不会出现分离现象。

电容储能E为：

此时激磁安匝峰值可表示为：

当激磁安匝高于衔铁释放阈值时，衔铁开始释放，其可能处于有限分离、临界分离或可靠释放状态。线圈激磁作用下衔铁所受力矩冲量越大，则衔铁实际释放过程中获得的角动量越大，越有利于可靠释放。电容不同，衔铁所获得的力矩冲量不同，电容容值从低到高增大时，力矩冲量随之增大，但电容容值增大到一定值时力矩冲量达到最大，该值为最佳匹配容值，如图6 所示。图中：(Ms-Me)dt所指示阴影部分与曲线表示衔铁所受力矩冲量。

图6 力矩与力矩冲量变化示意图Fig.6 Diagram of torque and torque impulse

若选取电容储能570×10-9J 作为基准值，由式（4）可以得到衔铁所受力矩冲量与电容的关系，如附录A 图A9 所示。在力矩冲量达到最大时获得最佳容值，其值为2.25 μF。

采用有限元计算模型仿真衔铁运动过程，电容在一定范围变化时，衔铁所受力矩与角位移如图7所示。

图7 储能相同而容值不同时衔铁受力与角位移曲线Fig.7 Torque and angular displacement of armature under same stored energy but different capacitor values

综合以上分析可知，不同容值下衔铁有3 种响应情况：

1）储能较低时，在任意容值下衔铁角动量与角位移均不能满足临界条件，而不能可靠释放；

2）在储能达到一定值时，有唯一电容使衔铁可以临界释放，此时的电容储能值即为衔铁临界释放所需的最小值；

3）储能超过一定值时，有2 个电容值使衔铁处于临界释放状态，储能电容在2 个电容值间可以保障衔铁可靠释放。

4 实验验证

电容储能释放过程只有几毫秒，且衔铁在临界分离条件下的角位移极小，很难直接测量衔铁所受磁力矩变化。因此在实际测量中，以衔铁可靠释放时电容的最小储能近似作为电容临界储能，通过观察磁脱扣器推杆是否被衔铁弹出，判断电容储能是否达到临界值，实验测试如附录A 图A10 所示。临界储能仿真与实验曲线如图8 所示，其数值及误差如表1所示。

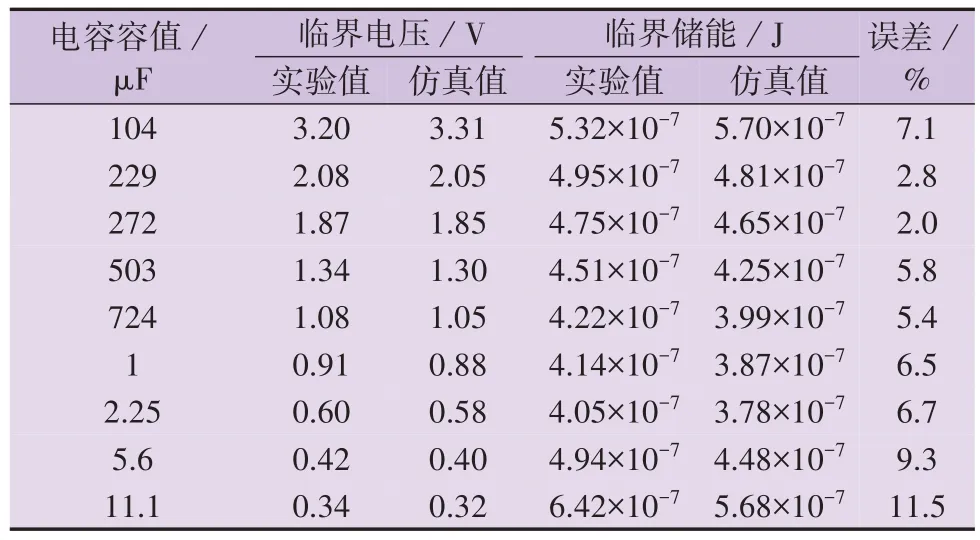
表1 实验与仿真储能误差Table 1 Energy storage error between experiment and simulation

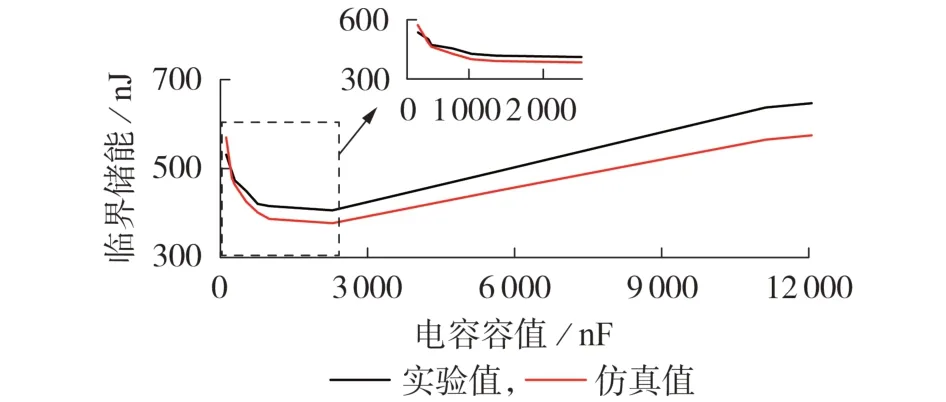
图8 临界储能的仿真与实验曲线Fig.8 Simulative and experimental curve of critical energy storage

由图8 可知，电容临界储能随电容增大而减小，但当电容增大到一定值时，电容继续增大，力矩冲量反而降低。在临界储能最小点，力矩冲量达到最大值，此时的电容值为最佳匹配电容值。误差主要来源于仿真模型与实际样机的参数不一致以及实验误差，根据电容储能公式（式（12）），电容储能与电容电压的平方成正比，电容越大，实验误差影响越大，因此在1 000 nF 以上误差较大。但仿真与实验结果呈现的变化规律一致，在实际中可以依据仿真结果确定初始参数，并通过实验测试来微调匹配电容。

5 结论

本文通过分析电磁式漏电保护器工作原理，建立磁脱扣器仿真计算模型，对磁脱扣器在不同激励源下的响应特性进行研究，对电容与磁脱扣器的匹配关系进行分析。通过对磁脱扣器样机进行实验测试，并与仿真结果对比分析，验证了理论分析与仿真计算的正确性。主要结论如下。

1）分析了电磁式漏电保护器基本工作原理，建立了磁脱扣器的数学模型与有限元计算模型，根据激磁安匝进行衔铁响应状态的判断，仿真分析了不同线圈激励形式下磁脱扣器衔铁释放响应状态。恒压源激励下磁脱扣器衔铁行为状态分为保持闭合、临界分离和可靠释放3 种行为状态，脉冲源与电容电压源下有保持闭合、有限分离、临界分离和可靠释放4种行为状态。

2）分析了衔铁临界分离时的受力变化与角动量变化轨迹，根据无激磁安匝下衔铁释放时临界角动量与角位移关系，确定了不同线圈激励形式下衔铁可靠释放的条件。在恒压源激励下衔铁可靠释放条件是稳态激磁安匝大于衔铁分离阈值安匝，在脉冲电源激励下衔铁可靠释放条件是衔铁最大角动量超过临界角动量，分离到受力平衡位置时的角动量大于0，在电容电压激励下衔铁可靠释放条件是激磁安匝为零时衔铁分离到受力平衡位置角动量大于0。

3）分析了电容电压激励下电容及其储能对衔铁所受力矩冲量的影响，得到衔铁释放所需临界储能与电容的关系，并确定了最佳匹配电容。在最佳匹配电容下，衔铁可靠释放所需临界储能最小，有利于缩短漏电保护时间，为实现漏电保护器的快速动作奠定了基础。

附录见本刊网络版（http：//www.epae.cn）。