应力波作用下红砂岩复合动态断裂特征研究

2024-01-18解北京李晓旭栾铮陈思羽陈铭进梁天宇

矿业科学学报 2024年1期

解北京,李晓旭,栾铮,陈思羽,陈铭进,梁天宇

中国矿业大学(北京)应急管理与安全工程学院,北京 100083

岩石的失稳破坏通常由岩石中的裂隙、气孔等原始缺陷扩展造成。在地铁隧道、煤矿巷道、地下硐室等岩体工程中,岩体结构可能受到各种类型动力扰动[1-3]。研究岩石中原生裂纹在应力波作用下如何起裂和扩展,进而了解原始缺陷对岩石动态断裂特性的影响,对于巷道安全掘进、岩体工程稳定性评价以及冲击地压动力灾害防治等具有重要的指导意义。

国内外学者对动态荷载下含预制孔洞、裂纹岩石试样的断裂行为开展了大量研究。张盛等[4-5]分析了预制裂缝长度对岩石动态断裂韧度测试值的影响。宋义敏等[6-7]采用落锤冲击试验机和数字散斑法,定量研究了冲击荷载下含预制裂缝岩石的位移场演化特征、裂尖张开位移、裂纹扩展速度、裂尖应力强度因子演化规律。李地元等[8]利用分离式霍普金森压杆(Split Hopkinson Pressure Bar,SHPB)和高速相机分析了不同层理倾角预制中心孔洞层状岩石的动态力学参数、裂纹扩展过程及破坏模式。龚爽等[9]分析了冲击荷载作用下含双孔洞裂纹石灰岩的动态抗压强度、动态变形模量、破坏模式和裂纹扩展行为。DAI 等[10-12]通过试验和数值模拟,研究了不同类型花岗岩试样的Ι 型动态断裂韧度,探讨了各向异性和加载速率等对其断裂性能的影响。LI等[13]利用超级计算机对两种非均质岩石表面三维裂纹萌生和扩展进行了数值模拟研究,再现了翼形裂纹、反翼形裂纹和类壳裂纹的萌生和扩展过程。武宇等[14]通过SHPB 实验发现,应力波波长和应力波幅值是影响砂岩损伤的主要因素。李成孝等[15]利用数值方法模拟了Ⅰ-Ⅱ混合型裂纹扩展轨迹。

前人研究大多集中在Ι 型动态断裂上,而对工程实际中更常见的复合型断裂(包含拉伸型和剪切型破坏)研究较少,同时对不同波长应力波影响下的岩石动态断裂特性也鲜有报道。为探究应力波的影响,以红砂岩试样为研究对象,结合SHPB装置和高速相机等设备开展动态三点弯曲实验,分析加载率、应力波长对红砂岩复合动态断裂特性的影响,为巷道掘进过程中冲击地压等动力灾害防治提供参考。

1 实验概况

1.1 试样制备

试样取自工程现场采出的新鲜完整红砂岩,颗粒均匀,无明显层理裂隙,均质性较好。根据国际岩石力学学会(ISRM)发布的半圆盘弯曲法(Semi-Circular Bending,SCB)测定岩石断裂韧度的推荐标准[16],通过钻取岩芯、磨平端面等工序,加工成直径(2R)50 mm、厚(B)25 mm 的圆盘试件,并按照预制裂纹长径比[17]0.35、角度(β)30°、长度(a)8.75 mm 的方案,切割成半圆盘试件共计16 个。制备完成的SCB 试样如图1 所示。

图1 SCB 试样Fig.1 Semi-circular bending specimens

1.2 实验系统

实验利用中国矿业大学(北京)煤岩动载破坏参数测试实验室直径50 mm 的SHPB 实验装置,开展红砂岩SCB 试样动态断裂实验,SHPB 实验系统如图2 所示。

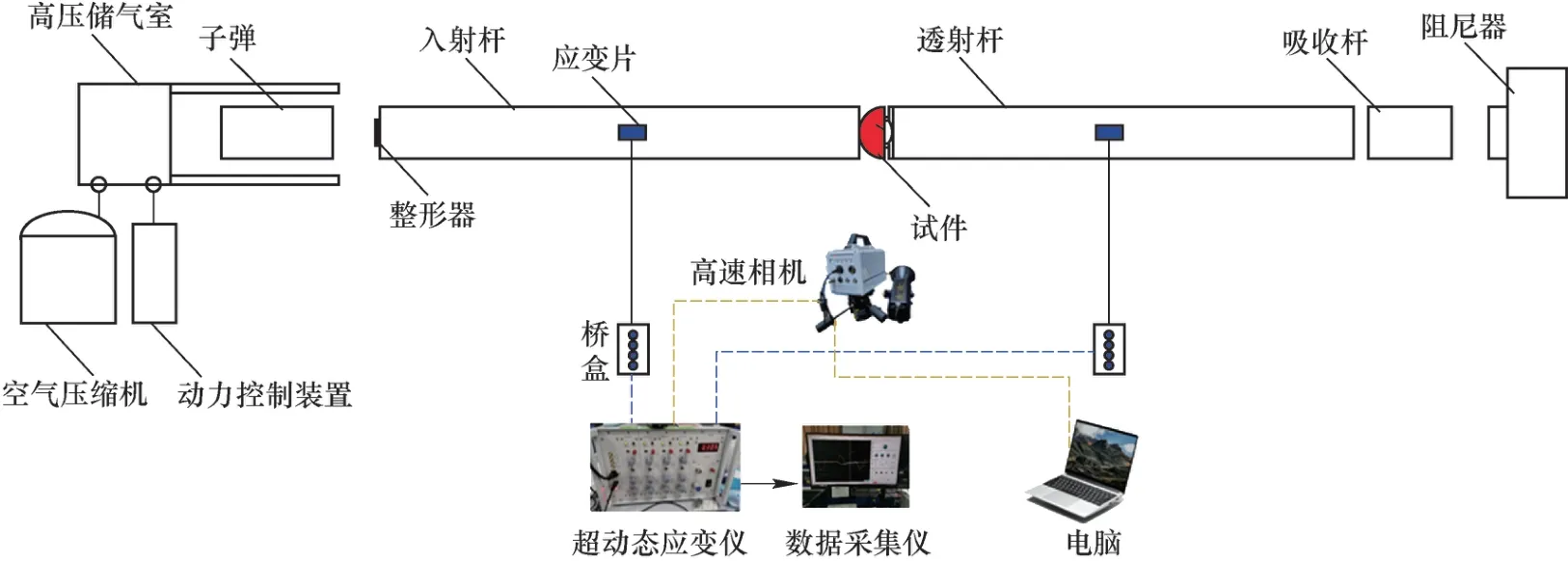
图2 SHPB 实验系统Fig.2 SHPB experimental device

SHPB 实验系统包括:冲击加载系统、轴围压系统、数据采集及处理系统。实验平台采用钢底座支撑,长度约12 m,配备导轨及中心架用于校准方向,以实现杆件系统轴向对中,避免横向误差。铝杆及子弹直径均为50 mm,选用圆柱型子弹长度分别为0.3 m、0.4 m、0.5 m,入射杆长度3 m,透射杆长度2.5 m,吸收杆长度1 m。铝杆及子弹均为合金铝,弹性模量72 GPa,屈服强度0.4 GPa,密度2 700 kg/m3,波速5 164 m/s。高速相机拍摄速度为100 000 fps,分辨率为320×192 px。

1.3 实验原理

SHPB 测试过程中,撞击杆高速碰撞入射杆,在撞击过程中杆件接触端将会产生应力脉冲信号,此应力波脉冲会继续沿入射杆传播。当到达入射杆件与试块接触端时,在应力波脉冲的作用下,试件产生一定程度的形变。同时,由于阻抗不匹配,一部分应力波反向传递至入射杆,产生拉伸波;另一部分透过试件传递至透射杆,产生正向压缩波。试样两端的加载力p1(t)、p2(t)分别为

因此,试样两端平均加载力p(t)为

式中,A为压杆横截面积,m2;E为压杆的弹性模量,GPa;εI(t)为压杆入射应变;εR(t)为压杆反射应变;εT(t)为压杆透射应变。

在SHPB 实验中,实验结果的可靠性由试件两端所受应力是否能达到平衡而决定[18]。因此,在实验开始前有必要验证应力平衡性。岩体试件两端的应力平衡验证如图3 所示,透射加载力基本等于入射应力与反射应力之和,因此岩石试件两端的应力平衡基本满足。对每个实验结果进行应力平衡验证,不满足应力平衡条件的实验结果不予采用。

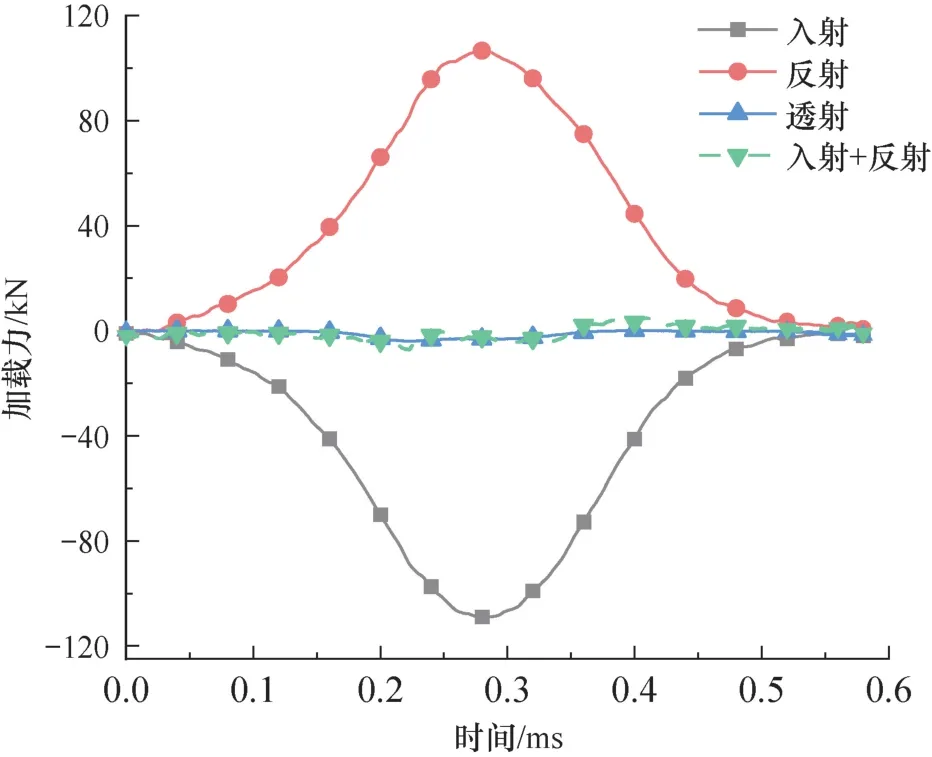
图3 应力平衡验证Fig.3 Verification of stress balance

图4 为不同长度子弹在相同冲击速度下的波形。子弹长度主要影响应力波长。由一维应力波理论[19]可知,SHPB 实验中波长λ为子弹长度的2倍,因此3 种子弹对应的λ值分别为0.6 m、0.8 m、1 m。

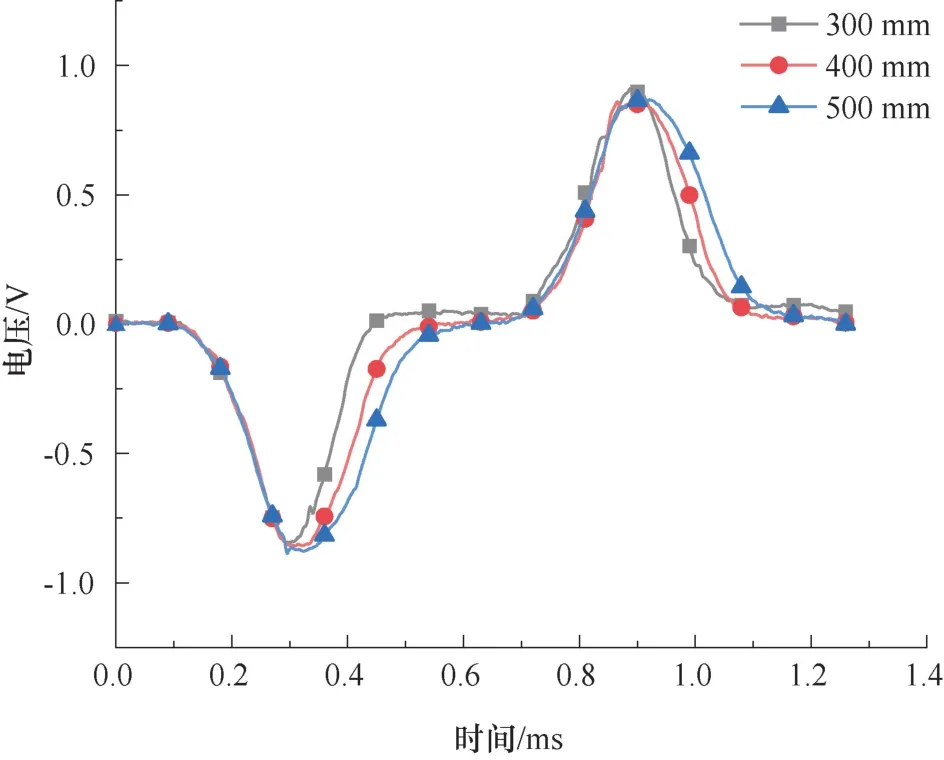
图4 不同长度子弹在相同冲击速度下的波形Fig.4 Waveforms of different bullets

2 动态抗拉及断裂力学特性

2.1 动态抗拉强度

2.1.1 抗拉强度计算方法

根据平面应变假设,准静态条件下试样的抗拉强度为[20]

试样几何构型的无量纲函数计算公式如下:

式中,S为试件底部两个支撑点跨距,m。

2.1.2 加载率计算方法

加载率是描述材料动态抗拉强度的重要参数之一[21]。岩石的强度特征大多存在率相关性[22],图5为半圆盘试样在波长0.6 m、冲击速度8 m/s 的应力时程曲线,可以看出,在达到峰值应力之前存在一个应力线性增长区间,该线性段的斜率即为加载率。

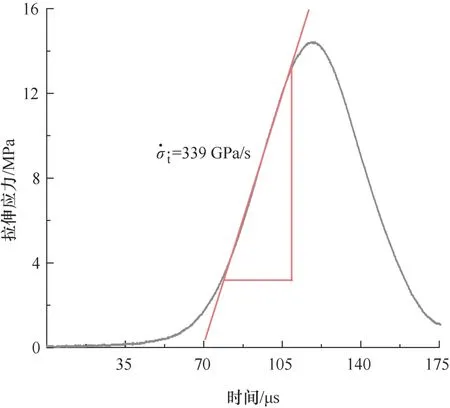
图5 拉伸应力时程曲线Fig.5 Tensile stress time-history curve

不同波长下加载率效应曲线如图6 所示。由图6(a)可知:3 种波长的加载率均随冲击速度的增大呈线性增大。应力波波长越大,加载率增长幅度越大。

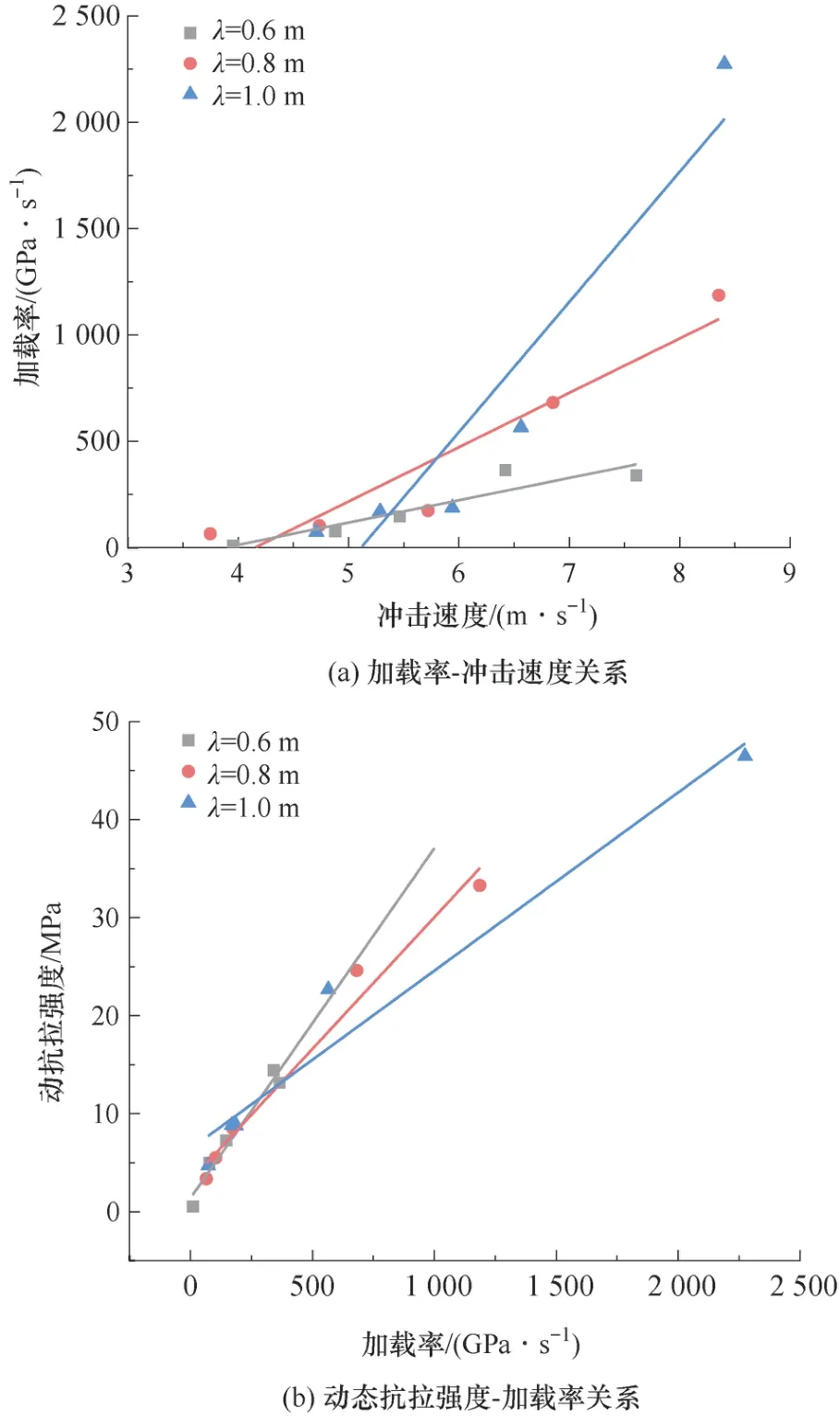
图6 加载率效应曲线Fig.6 Loading rate effect curve

由图6(b)可知,不同波长下红砂岩动态抗拉强度随加载率增大呈线性增大的关系。在0.6 m 波长下,动态抗拉强度为0.56 ～14.43 MPa,随加载率增大而增长了26 倍。在4 m/s 的冲击速度下,动态抗拉强度为0.56 ～3.36 MPa,随波长增加而增长了742.14%,表明动态抗拉强度与波长存在正相关关系。原因可能在于波长和加载率的增大促使试样吸收更多的能量,动载冲击下试件中的微裂纹未能及时起裂或贯通,导致试件变形滞后。这种滞后现象随着吸收能量的增加而愈发明显,宏观表现为动态抗拉强度的加载率强化效应[23]。

2.2 动态断裂韧度

断裂韧度是判断岩石断裂是否发生的关键参数。当加载力p(t)达到最大值时,由式(6)和式(7)计算的应力强度因子分别为纯Ⅰ型和纯Ⅱ型断裂韧度[24]。

式中,YⅠ、YⅡ分别为纯Ⅰ型和纯Ⅱ型断裂模式下的无量纲应力强度因子,为试样几何构型的函数。

改变试件预制裂纹角度β可以测得不同模式下的断裂韧度[25]。本实验的几何构型参数对应复合断裂模式,YⅠ=1.461,YⅡ=0.978[26]。为进一步揭示和表征岩石在复合断裂模式下的力学性质和行为,需计算复合型断裂模式下的等效断裂韧度Keff[27]:

式中,KIm、KIIm分别为按纯Ⅰ型、纯Ⅱ型断裂模式下计算的动态断裂韧度。

拟合得到的红砂岩动态断裂韧度-加载率关系如图7 所示。

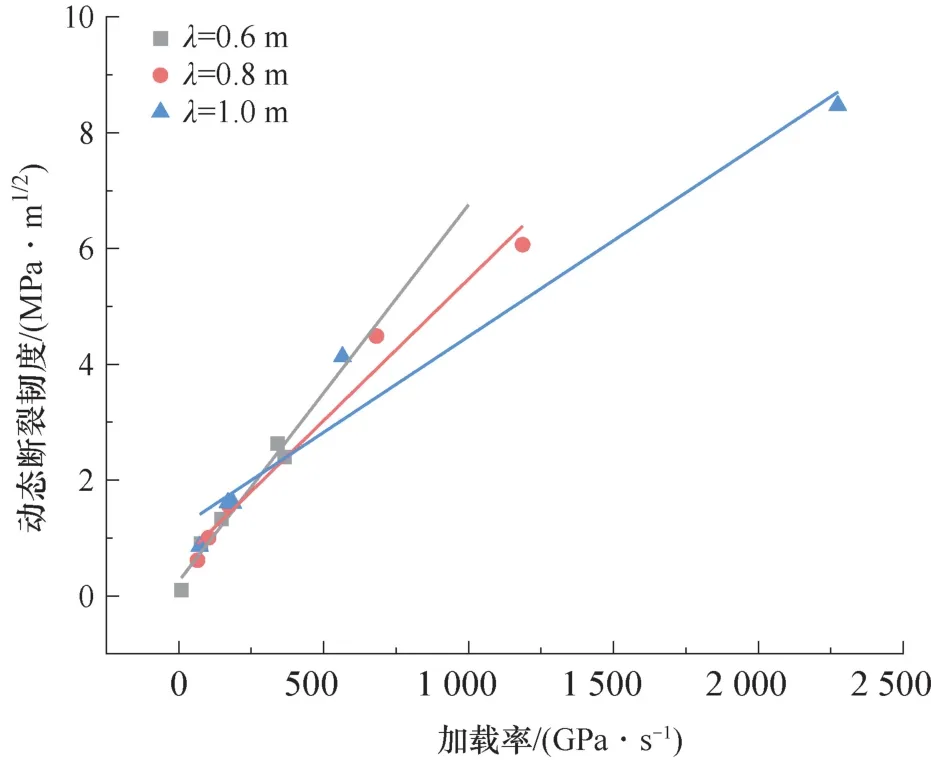
图7 动态断裂韧度-加载率关系Fig.7 Dynamic fracture toughness loading rate relationship

与红砂岩的应变率效应类似,在波长0.6 m 条件下,其动态断裂韧度随着加载率的提高而线性提高,动态断裂韧度范围为0.1 ～2.62 MPa·m1/2,随加载率增加而增长了26 倍。随着波长增加,动态断裂韧度的拟合曲线斜率不断下降,表明加载率对于动态断裂韧度的影响呈逐渐减弱的趋势。原因可能在于,波长较大时,应力波在试件中作用时间加长,能量传递速度相对减缓,试件中微裂纹起裂的滞后效应随之降低,因而试件抵抗内部裂纹扩展的能力有所下降。

2.3 动态能量耗散规律

根据SHPB 实验中的一维应力波传播理论和应力均匀假设,通过对杆件上的入射波、反射波和透射波数据积分的计算方式,求得与之对应的入射能、反射能及透射能[28]。

式中,WI为入射能,J;WR为反射能,J;WT为透射能,J;σI为入射应力,MPa;σR为反射应力,MPa;σT为透射应力MPa;C0为应力波波速,m/s。

在岩石动态断裂破坏过程中,总吸收能(ΔW)的一部分用于岩石内部新裂纹的产生,该部分能量称为断裂能[29],记为WG;另一部分能量则以试件中残余动能(K)的形式存在[30]。根据能量守恒定律可知:

对于半圆盘类试件,K又可表示为

式中,I为断后试件碎片的转动惯量,kg·m2;ω为试件碎片的角速度,rad。

由高速相机记录的照片并结合图像处理软件ImageJ,即可得到破坏后的红砂岩SCB 试件碎片在不同波长和加载率下的角速度时程变化情况。图8 为不同波长冲击下SCB 试件时间-转动角度,图9 为不同加载率下SCB 试件时间-转动角度。

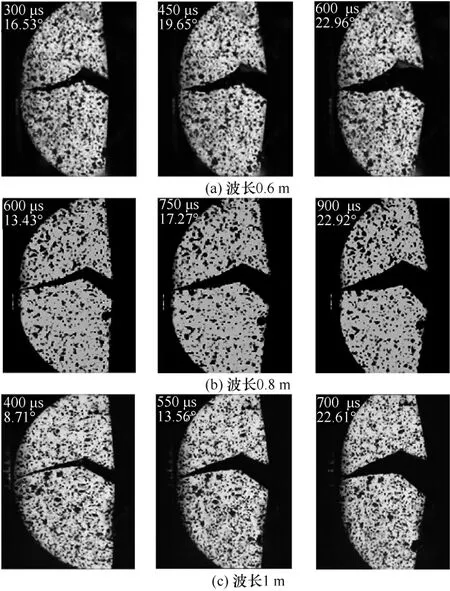
图8 不同波长冲击下SCB 试件时间-转动角度Fig 8 Time-rotation angle of SCB specimens under different wavelength

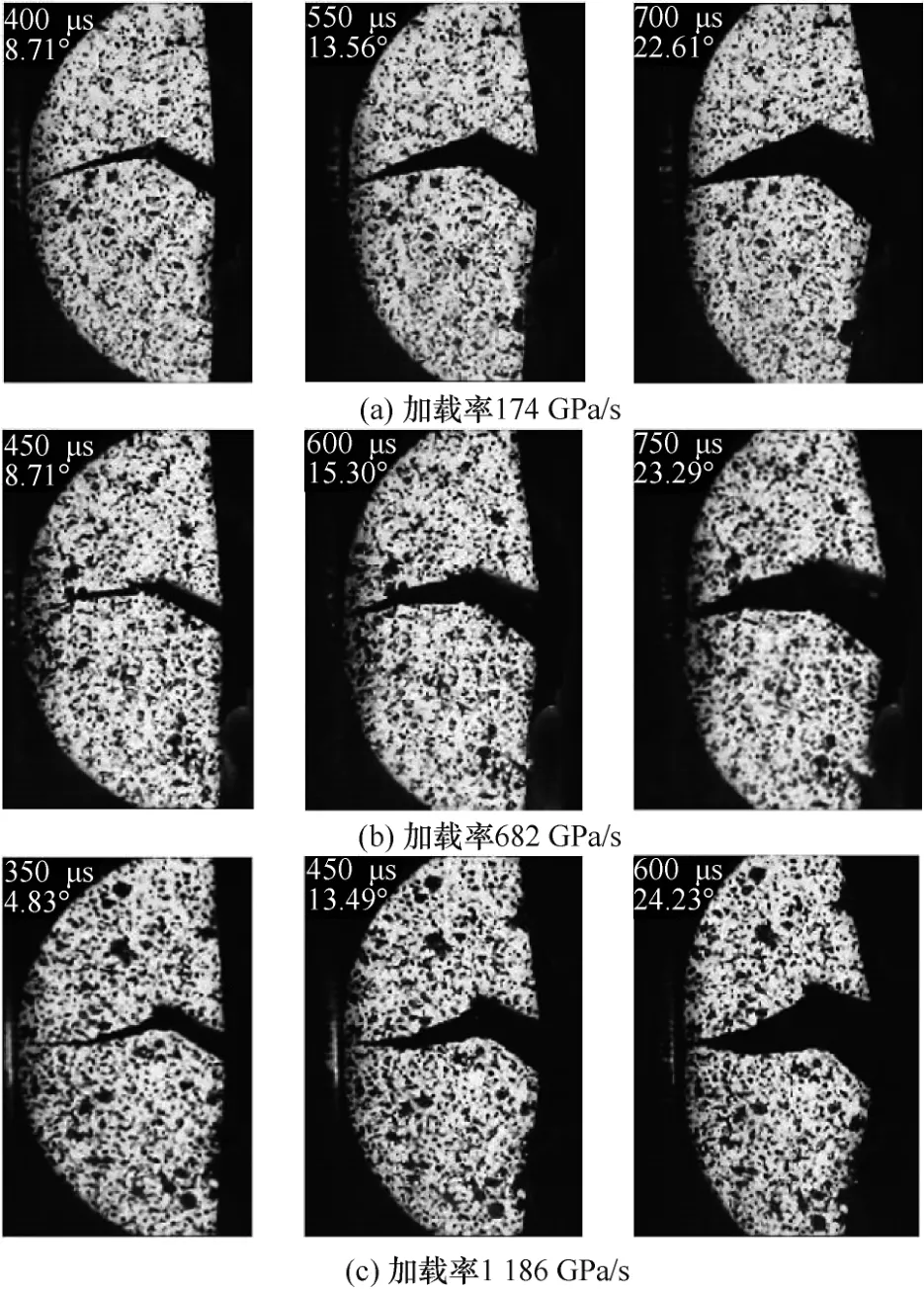
图9 不同加载率下SCB 试件时间-转动角度Fig.9 Time-rotation angle of SCB specimens under impacts of different loading rate

由图8 和图9 可知,随着波长增加,试件破碎的平均角速度增长了116.18% ;随着加载率增加,试件破碎的平均角速度增长了67.48%。试件破碎的平均角速度与波长及加载率具有显著的正相关关系。

图10 和图11 分别为红砂岩SCB 试件波长-能量关系和加载率-能量关系。由图可知,红砂岩SCB 试样中的入射能、吸收能、断裂能、残余动能均随加载率和波长的升高而增大。断裂能随加载率升高而增长了415.27% ,随波长升高而增长了54.49%。若定义实验中半圆盘试件的断裂能与入射能的比值为试件断裂能量吸收率δ,即

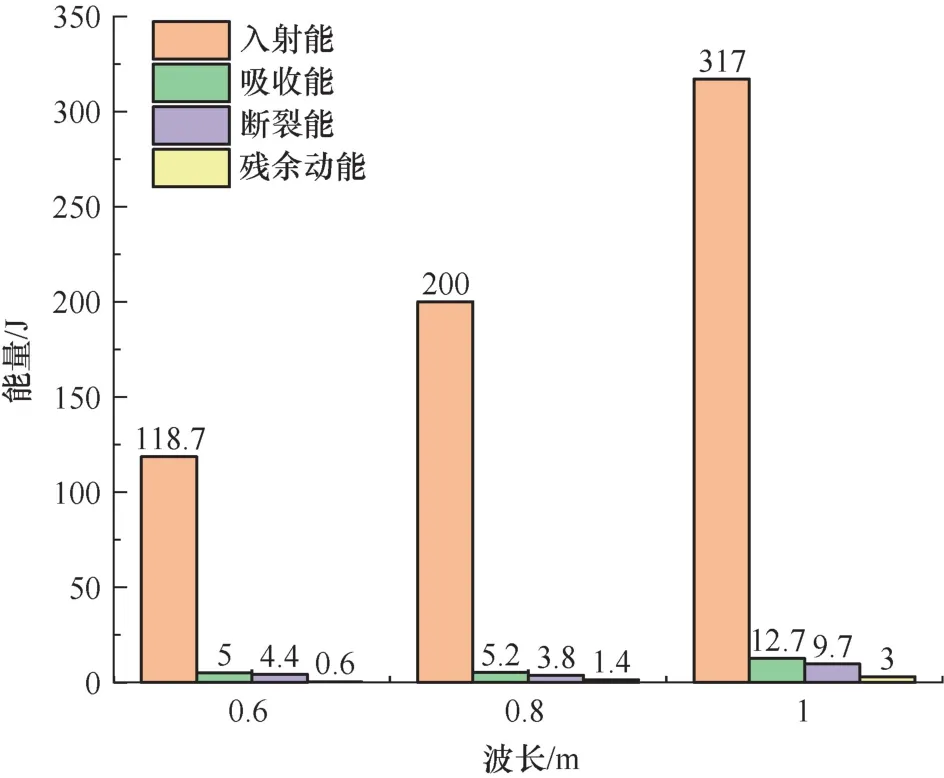
图10 波长-能量关系Fig 10 Wavelength-energy relationship

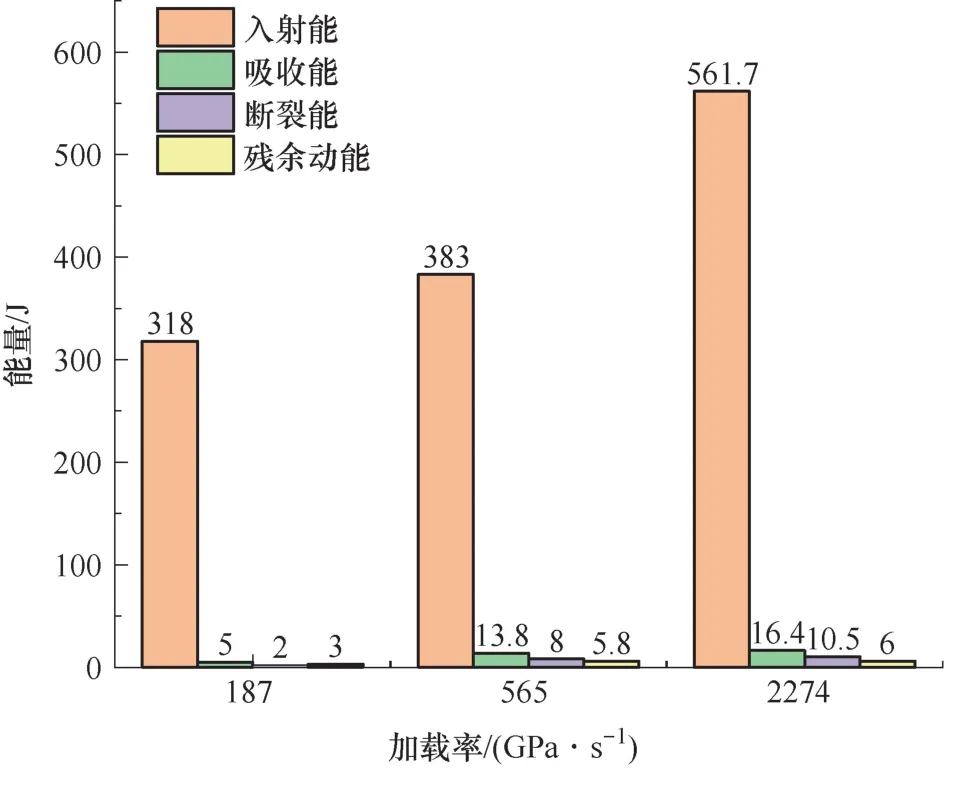
图11 加载率-能量关系Fig.11 Loading rate-energy relationship

通过计算,随着波长增加,断裂能量吸收率降低了17.79% ;随着加载率增加,断裂能量吸收率增长了190.63%。分析结果可知,随着加载率的提高,SCB 试件在动态断裂过程中的能量吸收率逐渐升高,用于断裂破坏时的能量有效转化率显著提升。而随着波长增加,即应力波作用时间增长,能量吸收率呈下降趋势,原因可能在于,岩石破碎吸收能量时受应力波幅值影响较大,因此应力波长不断增加时,入射能虽快速增长,但用于试样裂纹扩展的能量增长相对缓慢,导致能量吸收率下降。因此,在以红砂岩为主要岩体的高应变率爆破开挖工程中,应采取合适爆速的炸药以产生较短的应力波长,提高破岩的能量利用率。

3 动态断裂破坏特征

3.1 动态断裂变形场演化

试样破坏前后照片如图12 所示。根据试样破坏后的照片,选取裂纹扩展集中的区域进行计算,并在裂纹首尾位置分别布置监测点P1和P2。

图12 试样破坏前后照片Fig.12 Photos before and after sample damage

利用数字图像相关(Digital Image Correlation,DIC)技术可以准确记录岩石断裂过程中不易被肉眼观察到的微裂纹的产生与传播,结合VIC-2D 中的拉格朗日算法即可绘制试样的全场应变云图。

图13 为试样在不同冲击速度和波长下的垂直方向应变云图,图中正数表示拉伸,负数表示压缩。由图13 可知,在裂纹扩展初期,试件表面应变分布较为均匀,当积蓄的弹性能达到起裂阈值时,预制裂缝尖端出现明显的应力集中现象。随着裂纹的扩展,应变传导至裂纹末端,裂纹扩展区域的四周受压应力作用,试样同时受到拉伸和剪切作用,表明这是Ⅰ/Ⅱ复合型的裂纹扩展方式。4 m/s冲击下,随着应力波波长的增加,裂纹扩展区域底部受压应力影响的区域逐渐减少。8 m/s 冲击下,拉应力的主要影响范围自始至终集中在预制裂缝周围,几乎没有出现传导的现象。

图14 为不同冲击速度下监测点P1 和P2 应变时程曲线。由图14 可知,主裂纹首尾监测点位的应变在应力波扰动后,随时间快速增长,当弹性能达到起裂阈值时,应变达到峰值并由于破碎而迅速下降。随着应力波长从0.6 m 增加至1 m,裂缝尖端积蓄弹性能的时间随之增加,裂纹首尾应变增长均出现滞后现象。8 m/s 的冲击速度下,试件中吸收更高的断裂能,使主裂纹首尾监测点位的应变平均增加了84.31%。

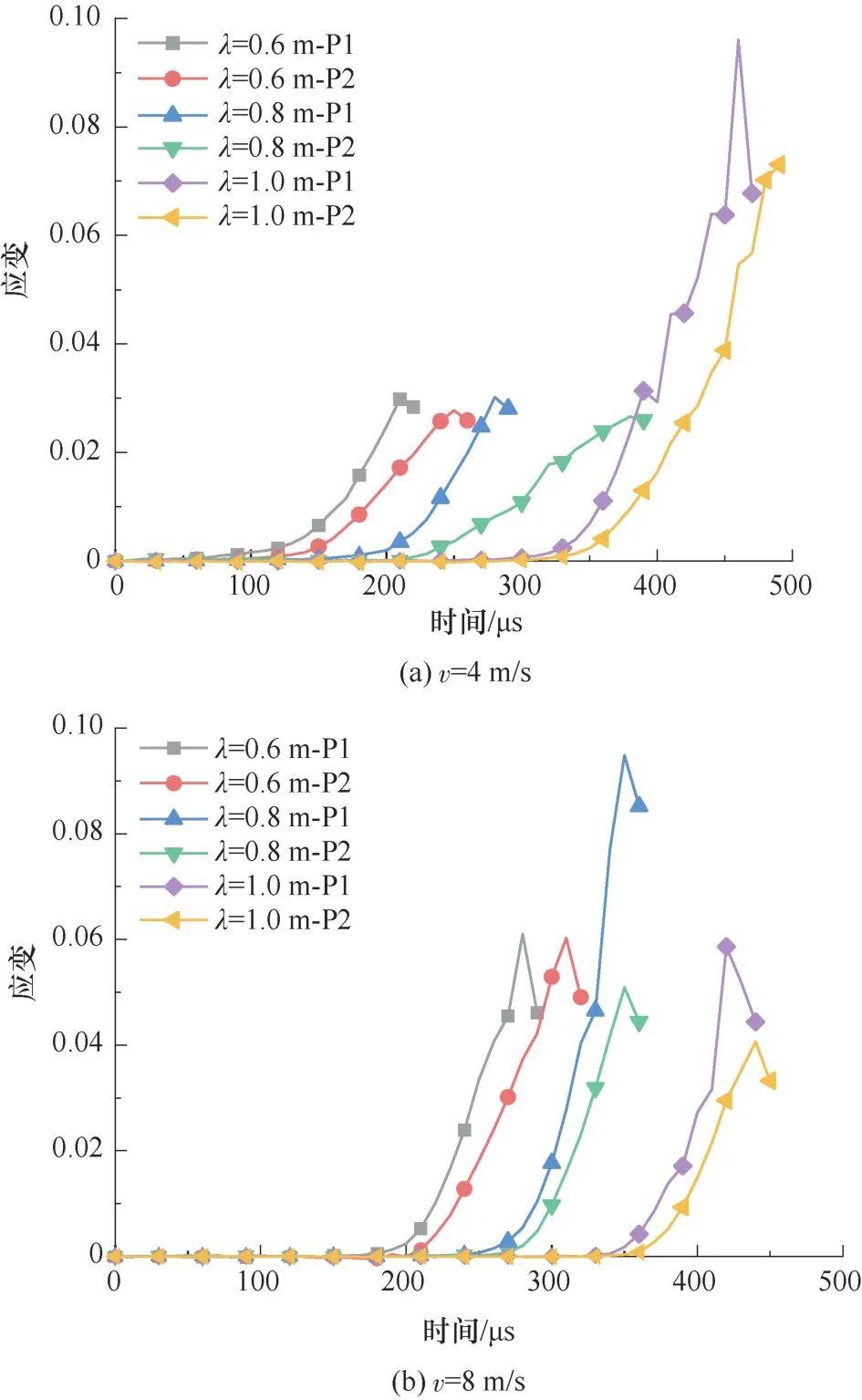
图14 不同冲击速度下监测点应变时程曲线Fig 14 Time course of strain at monitoring points under impacts of different velocities

3.2 动态裂纹扩展速度

裂纹扩展速度可显著反映动态断裂过程的裂纹传播特性。在试样背面粘贴LKYBP101212裂纹扩展应变片,用于监测裂纹扩展速度。裂纹扩展应变片尺寸为12 mm×12 mm,栅格数10,栅格间距为1 mm。裂纹扩展应变片的粘贴如图15所示。

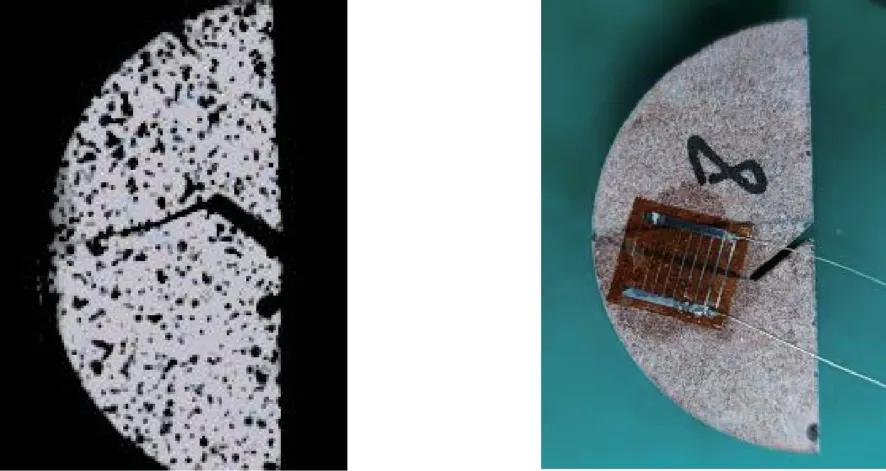
图15 裂纹扩展应变片的粘贴Fig.15 Adhesion of crack extension strain gauges

随着裂纹的扩展,10 条栅格依次断裂,导出裂纹应变片的电压时程数据如图16 所示。由图16可知,采集系统中所采集到的电压信号不断上升,整体呈台阶状。对电压时程曲线进行求导,电压与时间之间的导数可反映栅格的瞬间断开时间。对微分曲线再进行寻峰,即可获得裂纹扩展应变片10 条栅格断裂时对应的时刻。

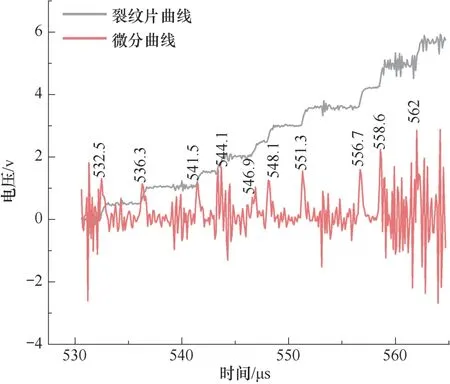
图16 裂纹扩展应变片电压时程曲线Fig.16 Voltage time history curve

图17 为不同波长下的裂纹扩展速度-距离曲线。由图17 可知,裂纹扩展的速度时程曲线整体表现为波动上升趋势,达到峰值速度后迅速下降。这是由于随着动态冲击荷载的施加,红砂岩试样内部的能量不断积累,导致裂纹一旦开始起裂,前期积累的能量得以迅速释放,从而初期裂纹扩展速度不断增大,最后能量传递趋于平稳,裂纹扩展速度相应下降。在同一加载率下,1 m 波长应力波造成的平均裂纹扩展速度和峰值裂纹扩展速度分别增长4.09% 和26.67%。

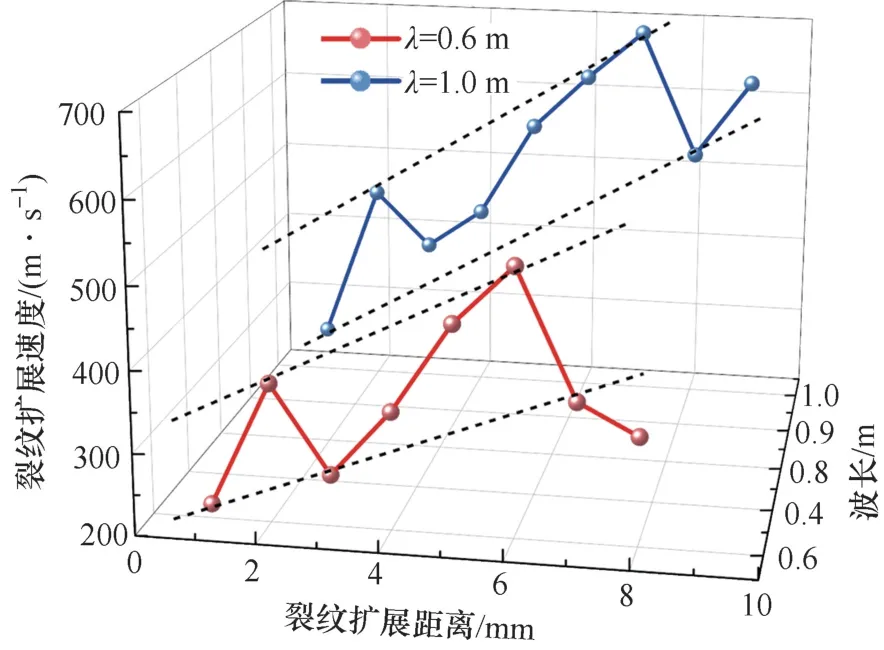
图17 不同波长下裂纹扩展速度-距离曲线Fig.17 Crack propagation velocity-distance curves at different wavelengths

3.3 宏观破坏特征

不同波长和冲击速度下红砂岩SCB 试样的破坏形态如图18 所示,不同应力波长扰动下的试样均存在显著的复合断裂破坏区域,多数试样的裂纹都由裂纹尖端向半圆盘顶部发育。

图18 波长-冲击速度破坏形态Fig 18 Wavelength-impact velocity damage pattern

同一波长下,随着冲击速度的不断增加,试样所产生的复合断裂破坏区域不断扩大,破裂面积随之增大。此外,应力波长的增大也使得破裂区域相应扩大,这是由于应力波作用在试样内部的时间越长,给试样带来的内部损伤越大。为定量分析冲击速度、波长对破坏区域的影响,绘制破碎试样图片素描图(图19)。

图19 试样破坏形态素描图Fig 19 Sketch of the damage pattern of the specimen

利用ImageJ 软件测量照片中的总面积和完整区域面积,计算出破坏区域面积,用破坏区域面积除以试样的总表面积即可得到试样的破坏区域面积占比,定义为破坏率。破坏率与冲击速度关系如图20 所示。由图中拟合公式可知,不同波长下加载率与破坏区域面积占比存在显著的线性关系。

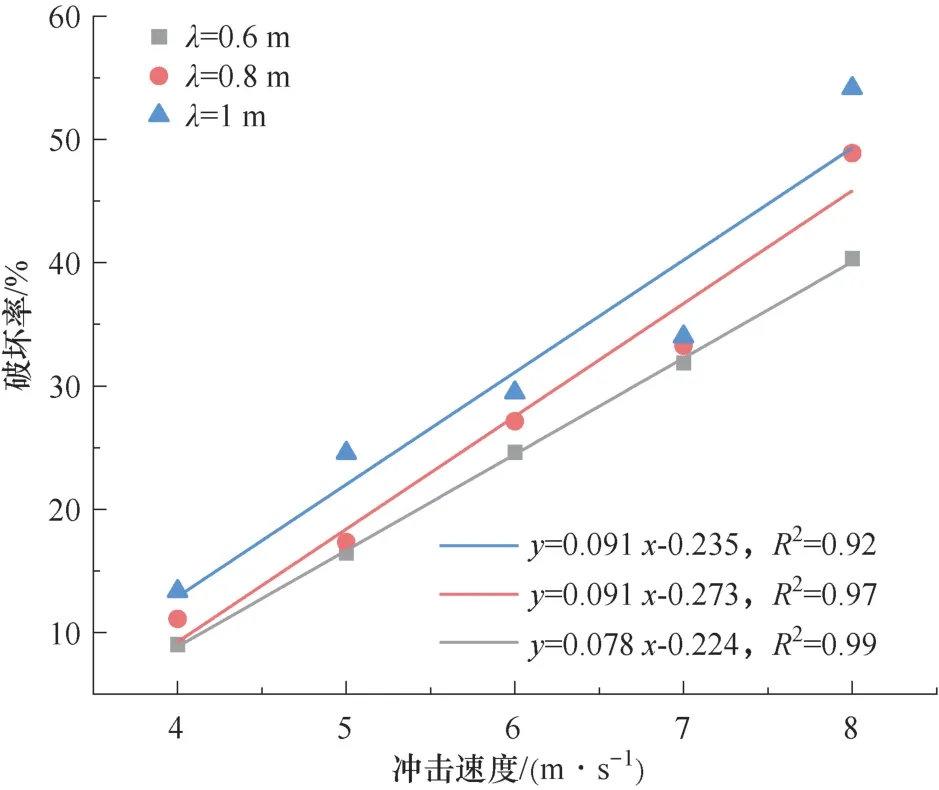
图20 破坏率与冲击速度关系Fig 20 Relationship between damage rate impact velocity

随着冲击速度的不断增大,破坏区域面积占总面积比例不断上升,破坏区域与冲击速度呈现出良好的正相关性。此外,破坏面积占比与应力波长之间也存在正相关性,随着应力波长的递增,破坏面积占比也相应扩大,1 m 波长应力波对SCB 造成的破坏增长率相较于0.6 m 和0.8 m 波长分别增长了17.31% 和5.49%。