分数评估法实现光通过散射介质聚焦

方龙杰,程科,何修军

(成都信息工程大学光电工程学院,四川 成都 610225)

1 引言

光散射成像技术是生物医学领域一项非常重要的技术。随着空间光调制器的迅速发展,波前调制在光通过散射介质聚焦和成像领域得到了广泛的研究[1-3]。这些研究成果在光声成像[4]、显微操作[5]、生物医学检测[6]、三维全息显示[7]、光纤通信[8]、超衍射成像[9]等领域具有广阔的应用前景。为了实现光通过散射介质聚焦,需要寻找与散射介质相匹配的输入光场,其中用到的算法包括:数字相位共轭法[10]、传输矩阵算法[2,11]和迭代反馈算法[12]。数字相位共轭方法利用共轭相位来抵消散射介质的随机扰动效应,但其光学系统较为复杂,且需精确校准[10]。传输矩阵方法通过建立输入光场和输出光场的线性关系实现聚焦,但难以获得高维度的传输矩阵,并且抗干扰能力较弱[13]。迭代反馈算法根据散射光场的实时反馈不断调节入射光场,使焦点的光强逐渐增大。这种算法操作简单,在实际应用当中易于实现[14]。常见的迭代反馈算法有蚁群算法[15]、麻雀搜索算法[16]等。然而,散射光场容易受到环境扰动而发生畸变,在噪声环境下难以实现输出光场的精准调控。

近年来,深度学习算法在散射成像领域得到了广泛的应用。该算法基于数据集建立输入光场和输出光场之间的映射关系,具有强大的拟合能力,在抗散射过程中展示出其独特的优势。例如,Horisaki等利用神经网络算法对散斑图像进行分类和重构[17]。Li等使用基于密集块的Unet网络实现相干光通过毛玻璃成像[18]。Unet网络具有架构简单、精度高、易于实现等优点,在散射成像领域得到了广泛的研究,但仅仅适用于薄散射介质的图像重建。对于厚散射介质的成像,这种方法将会失效。为了解决这一问题,Lyu等提出深度神经网络和混合神经网络结构,成功实现通过厚度为3 mm的聚苯乙烯散射介质成像,成像深度为介质平均自由程的13.4倍[19]。Guo等构建的抗散射卷积神经网络将散射成像的记忆效应范围扩大了40倍[20]。

深度学习算法虽然能够实现厚散射介质的聚焦与成像,但是要求散射介质为静态散射介质。而对于动态散射介质,深度学习算法则失效。因此,本文提出分数评估法实现光通过散射介质聚焦。根据线性传输光学系统的输入通道理论,散射聚焦的物理本质是保留对聚焦有益的输入通道,并且去掉对聚焦不利的输入通道。而对于聚焦不利的通道,如果将其附加π的相位值,则不利通道会变为有利通道。我们采取二元相位优化的方式提高迭代程序运行的速度,缩短聚焦时间,便于将其运用于生物成像。在实验中,将分数评估法与蚁群算法[15]对比,结果发现,在强噪声环境下,分数评估法仍能实现光通过散射介质聚焦,而蚁群算法则失效,说明分数评估法具有更强的抗噪声能力。

2 算法描述

分数评估算法的流程图如图1所示。首先,在空间光调制器上加载大量的随机相位分布(设总共加载N个相位分布)。为了实现快速聚焦,我们采用的相位板为二元相位板,即只含有0和 π 两个相位的取值。对于每一个随机相位分布,都用CCD相机记录经过散射介质后的散斑光强分布(总共有N个散斑光强分布)。本实验的目标是实现光通过散射介质聚焦,因此目标函数为

图1 分数评估算法示意图Fig.1 The schematic diagram of the score assessment algorithm

ftarget(S)=Ifocus

(1)

其中,S为空间光调制器的相位分布矩阵,Ifocus为焦点处的光强值。

接下来构造分数评估矩阵Xi(i= 1, 2, …,N)。Xi的维数是S矩阵的二倍,设S矩阵总共含有n个元素,则Xi矩阵含有n×2个元素,其中第一列代表相位 π 的分值,第二列代表相位0的分值。给分的原则按照焦点光强的大小赋分。例如,对于第一个随机相位分布,测得焦点光强为6,此时第一个空间光调制器单元取的是相位0,因此相位0给6分,相位 π 给0分,所以矩阵X1的第一行为0和6;第二个空间光调制器单元取的是相位 π ,因此相位 π 给6分,相位0给0分。以此类推,则可以找出每一个随机相位分布对应的分数评估矩阵。

最后,计算总的分数评估矩阵,方法是把所有的分数评估矩阵相加,即总的分数评估矩阵

(2)

矩阵X表示相位0和 π 获得的总分。比较0和 π 两个相位获得的总分,则优化位相分布Xopt应当选取总分较高的位相。例如,对于空间光调制器的第一个像素单元,相位 π 的得分是82分,而相位0的得分是48分,因此第一个像素单元的相位应该是 π 。分数评估法的物理实质是按照对焦点光强贡献的份额定量评估应采用同相还是反相。当焦点光强越高时,说明该位相为正确位相的概率越大,其得分应该越高;反之,如果焦点光强较低,说明该点位相正确的可能性更小,应当以较小的分数评估该相位值。

3 数值模拟

为了验证分数评估算法在噪声扰动下的抗散射能力,我们通过数值模拟使光通过散射介质聚焦,并将分数评估法与蚁群算法比较。数值模拟的光路示意图如图2所示。激光器发出的平面波通过空间光调制器进行相位调制,经过透镜汇聚到散射介质的前表面,然后经介质散射的光波用CCD接收。为了简化计算,我们假设CCD和空间光调制器的像素个数相同,散射介质为服从均匀分布的随机矩阵,聚焦的位置为CCD的中心处。根据光场传输的复振幅理论,散射输出光场Eout(x,y)可以表示为

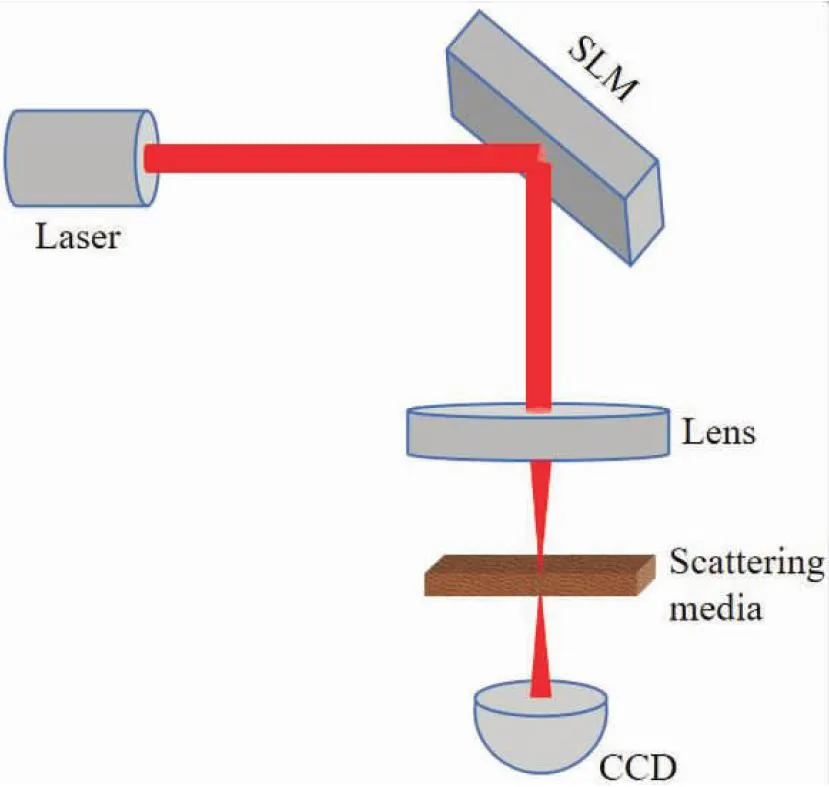
图2 数值模拟光路示意图Fig.2 Schematic of optical path in numeric simulation

Eout(x,y)=F{exp[iφSLM(x,y)]·exp[iφmedium(x,y)]}

(3)

其中,F表示透镜的傅里叶变换作用,φSLM(x,y)表示空间光调制器的相位调制作用,φmedium(x,y)表示散射介质的随机相位调制作用。CCD接收到的图像应为散斑光强分布,可以用下式表示:

Iout(x,y)=|Eout(x,y)|2

(4)

其中|Eout(x,y)|表示输出光场的振幅,Iout(x,y)表示CCD相机接收到的散斑光强分布。在每次数值模拟中加入随机噪声来比较算法的抗噪声能力。随机噪声大小与焦点光强有关,可以表示为

Inoise(x,y)=Iout(x,y)+μ·Iout(x,y)·δ

(5)

其中,μ是一个介于[-0.5, 0.5]区间的随机数;δ为比例常数,在模拟中取四个值:0、0.01、0.05和0.1,分别表示无噪声、加入方差为1%、5%和10%的高斯白噪声。

数值模拟中,所使用的空间光调制器像素单元个数是64×64=4096,仿真程序的迭代次数为10000次迭代。蚁群算法中采用的参数为:蚂蚁个体数量为100,初始转移概率p0为0.2,信息素衰减系数ρ为0.8,信息素浓度阈值(算法终止条件)为0.0001。这些参数的确定都是通过大量的模拟来优化参数,使模拟程序在当前条件下达到最佳状态,从而使比较更加客观。

图3展示了分数评估算法和蚁群算法在不同噪声情况下的增强因子随迭代次数的变化曲线。其中SAA表示分数评估算法,ACO表示蚁群算法。从图3(a)可以看出,在不引入噪声的情况下,分数评估算法在迭代10000次后的增强因子与蚁群算法的增强因子基本相同。需要指出的是,分数评估算法的初始增长斜率明显高于蚁群算法,但在之后的迭代中,增长斜率逐渐放缓,这主要是因为相位优化已经接近于饱和状态。当引入随机噪声时,从图3(b)-(d)可以看出,在相同的噪声环境下,分数评估算法得到的焦点增强因子高于蚁群算法,从而获得最佳信噪比。同时也证实了分数评估算法在散射聚焦和成像方面具有较好的抗噪能力。值得注意的是,分数评估算法不仅在增强速率上比蚁群算法更快,而且在相同条件下,与蚁群算法相比,获得最优解所需的迭代次数更少。造成这种结果的主要原因是两种算法不同的工作机制。蚁群算法在优化过程中具有随机性,可能会使得当前解偏离最优位置附近。而分数评估法是通过在现有最佳相位分布的基础上探索更优的解决方案。

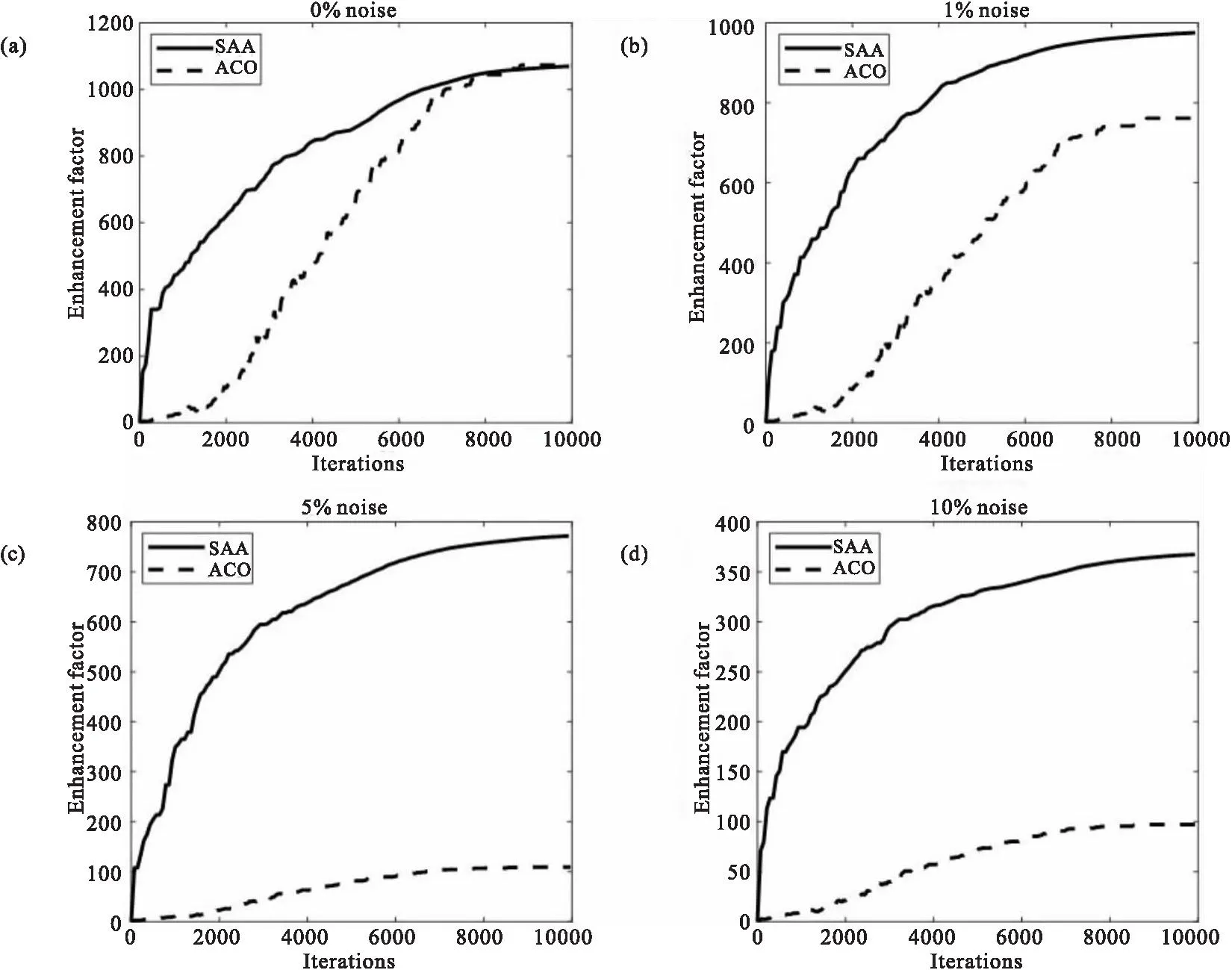
图3 不同算法在不同噪声下的增强因子。其中SAA表示分数评估算法,ACO表示蚁群算法。(a) 无噪声情形;(b) 加入1%的噪声;(c) 加入5%的噪声;(d) 加入10%的噪声Fig.3 Enhancement factors of different algorithms under different noise level. SAA means score assessment algorithm, and ACO means ant colony algorithm. (a) no noise; (b) 1% noise; (c) 5% noise; (d) 10% noise

在数值模拟中,分数评估算法采用的迭代次数是10000次。原则上讲,实验次数越多,焦点光强越大。而从模拟结果可以看出,迭代10000次时焦点光强已达到饱和,因此选取10000次迭代是可行的。在实际应用中,迭代次数由介质的特性确定。如果散射介质是动态的,则需要在介质的去相关时间内完成迭代优化,否则会因为介质的变化导致聚焦失败。在实际应用过程中,也会存在大量的随机误差,实验次数越多,累积的随机误差也越多。因此,需要在焦点光强达到预期值时立刻终止实验程序,防止误差累积太大。

4 实验

聚焦实验采用的实验装置图如图4所示。波长为532.8 nm的激光器(MSL-FN-532.8 nm-200 mw,CNI)发出圆偏振光,经过偏振片P1产生线偏振光,然后通过由透镜L1(f=150 mm)和透镜L2(f=250 mm)组成的4f系统扩束。扩束后的光通过偏振片P2改变偏振方向,并且偏振片P2的偏振方向与空间光调制器(Holoeye PLUTO-TEL-CO,1920×1080像素)的纯相位调制工作模式的偏振方向一致。旋转偏振片P1和P2可以调节入射光的强度。经过空间光调制器反射的光波通过透镜L3(f=100 mm)和L4(f=50 mm)缩束,并使用10×显微物镜(OL1,NA=0.25)将光聚焦到散射介质的前表面。本实验使用的散射介质为毛玻璃。经过介质散射的光通过20 ×显微物镜(OL2,NA=0.4)成像到CCD(Point Grey Research,Blackfly BFLY-U3-23S6M)上,并将接收到的图像输入计算机,可获取焦点光强。

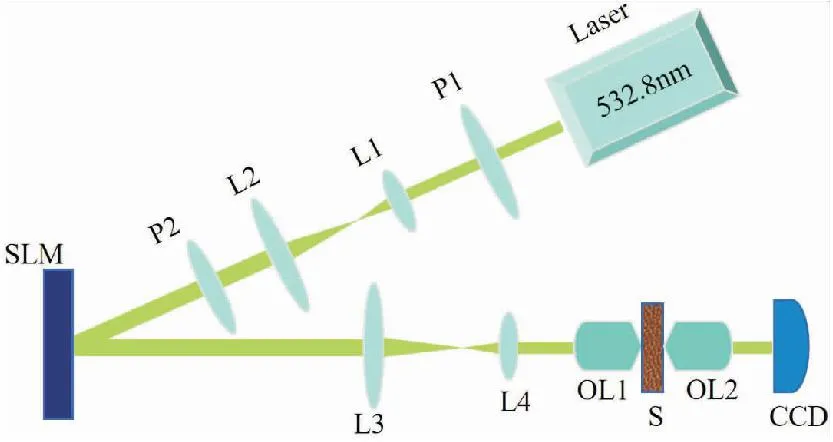
图4 散射聚焦的实验装置图。其中P1、P2为偏振片;L1、L2、L3、L4为透镜;SLM为空间光调制器;OL1、OL2为显微物镜;S为散射介质;CCD为电荷耦合器件Fig.4 Experimental setup for focusing light through scattering media. P1, P2: polarizer. L1, L2, L3, L4: lenses. SLM: spatial light modulator. OL1, OL2: objective lenses. S: scattering medium. CCD: charge coupled device

实验得到的聚焦效果如图5所示。为了比较在强噪声和弱噪声情况下两种算法的抗噪声能力,我们通过调节激光器的输出功率产生两种不同的噪声环境。激光器的最大输出功率是200 mw,将激光器输出功率分别调为200 mw和100 mw,对应的噪声大小为10%的噪声和30%的噪声。此百分比为测量30分钟内输出光强的均方差占输出功率均值的比例,噪声来源包括光学平台的振动、激光器输出功率的不稳定、实验室的杂散光等等。图5a为分数评估算法和蚁群算法的聚焦结果,其中SAA为分数评估算法,ACO为蚁群算法。可以看出,当噪声为10%的情况下,两种算法均能够得到焦点,分数评估算法的焦点光强为优化前散斑平均光强的71.4倍。而在强噪声条件下(30%噪声),蚁群算法失效,而分数评估算法仍然能够得到焦点。图5b和图5c分别为两种算法在10%和30%噪声下焦点增强因子随迭代次数的演化曲线。可以看出,当噪声为10%时,蚁群算法的最终增强因子为66.7,与分数评估算法的增强因子基本相同。但是,当噪声为30%时,蚁群算法的最终增强因子下降为4.1,而蚁群算法的增强因子为51.6。说明分数评估算法的抗噪声能力高于蚁群算法。

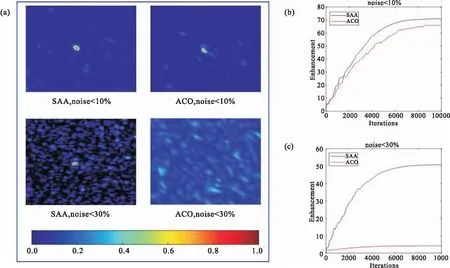
图5 实验得到的聚焦结果。(a)最终聚焦结果;(b)10%噪声下的增强曲线;(c)30%噪声下的增强曲线Fig.5 Experiment results of focusing. (a) Final focusing results. (b)Enhancement curves of 10% noise. (c) Enhancement curves of 30% noise

5 讨论

在分数评估算法的数值模拟部分,我们采用二元位相调制方法,获取聚焦的优化位相分布。假设采取连续位相调制方法,以空间光调制器的调制单元数为64×64=4096为例,迭代次数为10000次,在[0, 2π]区间等间距取16个相位,获得的焦点增强倍数如图6所示。为了讨论散射的随机性对最终焦点增强倍数的影响,我们总共进行30次模拟。二元位相调制方法同样也进行30次模拟,获得的最终焦点增强倍数也展示在图6中。对于每一种方法,所有的增强因子按照升序排列。从图6可以看出,连续调制方法的增强因子高于二元位相调制方法的增强因子。对于30次数值模拟,连续调制算法的平均增强因子是1101.4,二元调制方法的平均增强因子是1004.7。连续调制算法的增强倍数仅仅比二元调制算法高出9.7%。而从测量时间的角度来看,用二元调制方法需要的测量次数为2×10000=20000次,而用连续调制方法,需要的测量次数是16×10000=160000次,是二元调制方法耗时的8倍。因此,采用二元调制方法完全是可行的。

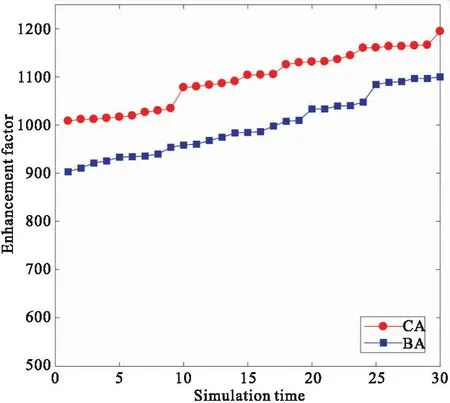
图6 连续调制方法和二元调制方法的焦点增强因子。其中CA表示连续调制方法,BA表示二元优化算法Fig.6 Enhancement factors of continuous algorithm and binary algorithm. CA means continuous algorithm, and BA means binary algorithm

分数评估算法的前提假设是,相位调制单元对聚焦的贡献是确定的。但是,由于寻找优化位相分布这一问题是多解问题,每一个调制单元的相位其实与其他单元的相位有关,它们是相互干涉后的结果。因此,通过分数评估算法得到的优化位相分布其实是众多优化解当中的一个。在相位优化过程中,由于随机噪声的引入,会使得局域相位值发生改变,因此对于同一散射介质,不同的实验次数得到的优化结果会不同。我们对比了同一散射介质,调制单元数64×64=4096,加入10%的噪声情况下,5次模拟得到的优化位相分布,结果如表1所示。从表1可以看出,由于噪声的影响,每一次获得的相位分布均不相同,但是都能够获得聚焦效果,说明这是一个多解问题,并且随机噪声的扰动会对实验结果产生影响。

表1 五次数值模拟得到的优化位相数量统计(调制单元数为64×64=4096)Table 1 Statistics of the number of optimized phases obtained by five numerical simulations (number of modulation units 64×64=4096)

6 结论

本文提出了一种基于分数评估的方式控制入射光场来实现光通过散射介质聚焦。与蚁群算法相比,分数评估算法具有较强的抗噪声能力,能够实现强噪声环境下的散射聚焦。分数评估算法利用二元相位优化,提升了散射聚焦优化过程的速度,缩短了聚焦时间,可将该方法用于动态散射介质的聚焦和成像。通过实验获得分数评估法的焦点光强是优化前散斑平均光强的71.4倍。总体而言,分数评估法有效地实现了散射光场的控制,在生物成像、医学诊断、生物组织实时监测等领域具有广阔的应用前景。