考虑机器人故障的生产线工位冗余设计
2024-01-16张于贤盛铁锋钟素红周梦婷
张于贤,盛铁锋,钟素红,周梦婷,岳 芳
(桂林电子科技大学 商学院,广西 桂林 541004)
随着科学技术的快速发展,先进制造技术正在从自动化、信息化向智能化方向发展,智能制造形态将成为未来制造业发展的主要方向和基本形态。在智能制造形态下,工业机器人将成为新型“劳动者”进行一线作业。在传统制造形态下,由于生产一线的作业者是普通工人,其生理、心理及情感等因素对生产系统的管理有重要影响。而对于智能制造形态下的工业机器人,它没有生理、心理及情感等特征。但它作为一种高度自动化、信息化甚至智能化的机器,具有较高的标准性及同质性。因此,就生产线而言,传统的人工作业生产线管理理论和方法不适合智能制造背景下工业机器人生产线的管理。
1991 年Rubinovitz 等[1]将一些更现实的约束增加至自动化生产装配线平衡模型中,首次提出机器人装配线平衡问题 (robotic assembly line balancing problem, RALBP) 这个概念。目前关于RALBP 的研究主要集中在构建适合自身需求的机器人装配线模型,并开发相应的启发式算法对模型进行求解。周炳海等[2]为了优化装配线平衡效率和提升制造过程的能源利用效率,在RALBP 基本约束的基础上加入执行能耗、换模能耗、待机能耗、工件传输能耗等能源消耗约束,构建了工作站数量最小化和总能耗最小化多目标机器人装配线平衡模型。Gao 等[3]基于确定的工作站数量,构建周期时间最小的RALBP模型,并运用一种局部搜索混合的新型遗传算法进行求解。雷卫东等[4]在自动化生产线调度上增加处理时间窗口约束、机器人搬运能力约束和工作站能力约束,并构建了此问题通用模型。Nilakantan 等[5]采用仿生算法实现U 型机器人装配线能源消耗最小化。故障因素是影响工业机器人作业状态的主要原因,是自动化生产线管理的一个重大挑战。张炎亮等[6]用粒子群算法对特征数据进行筛选、优化,并结合决策树模型中的信息熵将故障诊断的特征向量提取出来,极大提高了机器设备的故障诊断正确率。Johri[7]设计了用于求解具有有限缓冲区的自动化生产线产能的迭代算法,使管理人员可以及时调整缓存区大小以适应工位机器人工作状态转换。Kalir 等[8]设计一种启发式算法,能分别在缓存区有限和无限条件下合理设置各工位机器人数量,从而使生产线总成本最低。然而,在生产线上安装缓冲区需要大量的资本投入且占用稀缺的工厂空间。传统人工作业生产线通常通过多技能工人的运用,解决因产量增加、工位突发事故等因素引起的生产线不平衡与产能下降的问题。这种运用多技能工人的方法实际上相当于增加了作业人员的冗余功能,以此来提升生产线的产能[9]。冗余设计又称余度设计技术,是指对系统或设备完成任务起关键作用的地方,增加一套以上相同功能的功能通道、工作元件或部件,以保证当该部分出现故障时,系统或设备仍能正常工作,减少系统或设备的停机率,提高系统可靠性。章海波等[10]以工业机器人为对象,基于可靠性等理论构建了单台、多台协作的工业机器人标准工时计算模型。
本文针对各工位工业机器人功能差异较大、作业复杂度低且成本较低的简单作业机器人生产线,基于可靠性冗余设计原理、概率论及生产线平衡理论,在考虑故障因素影响下,对生产线各工位机器人配置数量问题展开研究,构建并求解简单作业机器人生产线工位机器人数量配置优化模型,缩小工业机器人生产线产能估算与实际产能之间的偏差,为工业机器人生产线的优化管理提供一种新思路和新方法。
1 工位作业机器人数及备份机器人配置数量分析
1.1 问题描述及相关假设
1.1.1 问题描述
假设某工业机器人生产线将所有需要完成的工序,按照产品生产工艺流程分为l个工位,每个工位上有ni个并行作业的机器人用于完成产品各工序的作业。同时,为保障工位上并行作业机器人发生故障时的生产连续性,各工位配置了mi数量的备份机器人。其中,备份机器人的作用是在并行作业的机器人出现故障时,临时顶替故障作业机器人进行工作,当故障作业机器人修复后又重新恢复到备份状态,避免因机器人故障导致生产率下降。现需要在满足生产节拍要求的前提下,以工业机器人投入成本最低为目标,设计一条工业机器人生产线,以确定各工位最适宜的作业机器人数量ni和备份机器人数量mi。同时,由于工业机器人的作业时间相对稳定,为降低中间库存的数量,所设计的工业机器人生产线各工位作业时间应尽可能均衡。
1.1.2 相关假设
本文构建相关模型基于以下基本假设。
1) 产品的生产目标已知,即工序预设生产节拍时间Tmb已知。
2) 生产该产品的工业机器人生产线所需的工位数量以及工位所需完成作业已知。
3) 工业机器人的考虑故障因素的标准作业时间t和无故障作业时间T可通过工业机器人标准工时测定方法[11]进行测定计算得到。
4) 各个工作站由传送带连接或由agv (automated guided vehicle, 自动导向车)小车进行物料搬运,传送时间可忽略不计。
5) 由于备份机器人是临时顶替故障的并行作业机器人进行工作,在并行作业机器人故障修复后又重新恢复至备份状态。备份机器人在并行作业机器人发生故障时也发生故障的概率较低,因此本文将备份机器人看作是完全可靠,即将备份机器人的可靠性设置为1。
为便于描述模型间数量关系,对相关变量参数进行说明,如表1 所示。

表1 工位工业机器人配置参数设计Table 1 Parameter settings of industrial robot workstation configuration
1.2 简单作业机器人生产线工位时间计算
1.2.1 工位正常工作工业机器人数量对应概率确定
为确定工位上正常工作的工业机器人数量对应概率,引入N模冗余系统来描述工位上工业机器人作业状态。N模冗余系统是一种由多个子系统和一个表决器组成,用于描述系统处于不同状态概率的计算机可靠性模型。如图1 所示。N模冗余系统中有N个可靠性为Rk(k=1,2,···,N) 的子系统,当有n个子系统处于正常工作状态时,系统处于完全可靠状态。N模冗余系统完全可靠的概率p为
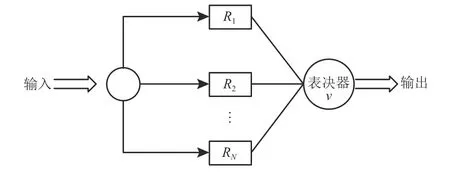
图1 n +m 模冗余系统Figure 1 An n +m mode redundancy system
类比于N模冗余系统,假设在工业机器人生产线上某个工位,设置了n个可靠性均为Rk的并行作业机器人以及m个备份机器人。本文将每个工业机器人视为一个独立的子系统,并将工位上工业机器人的作业看作是一个n+m模冗余系统。由于备份机器人的作用是临时替代故障的并行作业机器人进行工作,并在其修复后重新恢复到备份状态,因此备份机器人可以视为完全可靠。同时,当工位上并行作业机器人出现故障时,备份机器人能够及时替代,使得整个生产过程可以等价于始终有n个工业机器人正常参与工作。利用式 (1) 结合可靠性相关理论,可以计算得到工位上正常参与工作的工业机器人数量对应的概率分布,如表2 所示。
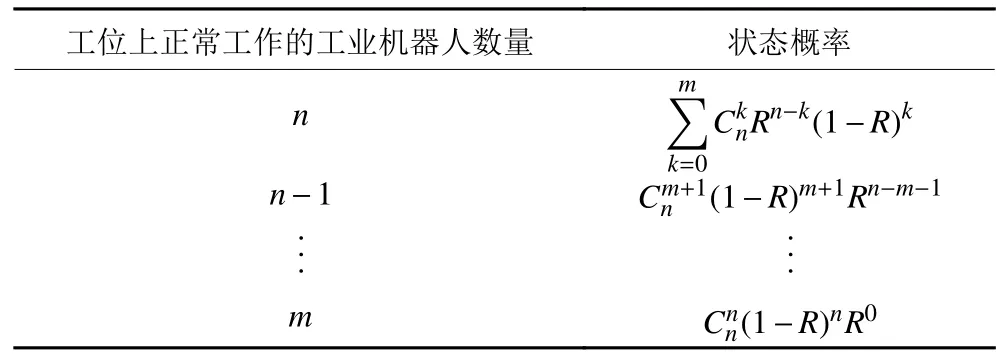
表2 工位无故障作业机器人数概率分布Table 2 The probability distribution of the number of trouble-free operating robots at a workstation
1.2.2 工位作业时间计算
1) 单个工业机器人工位作业时间确定。
当零部件的可靠性为100%且生产环境不发生变化时,单个工业机器人对应的工位作业时间等于工业机器人无故障作业时间乘以宽放率,如式 (2) 所示。
其中,T工位表示的是工位作业时间;T表示的是机器人无故障作业时间;A表示的是宽放系数;R表示的是工业机器人的可靠性。
在实际生产过程中,受零部件可靠性不是100%以及生产环境变化等影响,工业机器人不可避免地会出现故障。当工业机器人在生产过程中发生故障时,其完成产品的时间不仅包括实际生产产品的时间,还包括出现故障后停滞等待维修以及故障维修的时间。因此,此时工位的作业时间T工位等于考虑故障因素影响的工业机器人标准工时t。类比于传统生产线中测定标准工时的方法,考虑故障因素影响的工业机器人标准工时主要由无故障作业时间、故障时间和管理时间3 部分构成,如图2 所示。
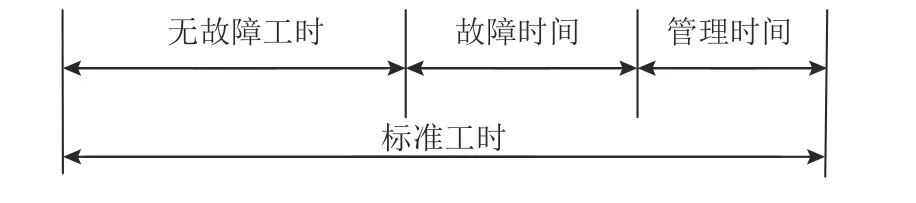
图2 工业机器人标准工时构成Figure 2 Composition of standard working hours for industrial robots
由图2 可知,当工业机器人发生故障时,单工业机器人工位作业时间计算公式为
其中,t为考虑故障因素影响的工业机器人标准工时;Rg为故障g发生的概率;Tg为工业机器人发生故障g时的故障时间。
综上所述,基于可靠性理论可以计算得到单工业机器人的工位作业时间计算公式可以表示为
由于宽放系数值不影响后续理论的证明,为简化相关推导,将宽放量设置为1,单工业机器人工位作业时间计算公式可以简化为
2) 多个工业机器人工位作业时间确定。
假设完成一件产品的生产需要该工位生产零部件a件,基于可靠性理论,结合表2,推导得到工位上不同数量工业机器人正常作业时对应的工位作业时间,如表3 所示。

表3 n+m 模冗余系统工位作业机器人标准作业时间Table 3 The standard operating time for operating robots at workstations in an n+m mode redundancy system
在得到工位上不同数量正常作业的工业机器人对应的概率和工位作业时间的基础上,通过概率论理论推导出多工业机器人工位作业时间计算公式,如式 (6) 所示。
2 工位机器人数量配置模型建立
本文在式 (6) 工位作业时间计算公式的基础上,构建了满足生产节拍要求下,以最优化工业机器人投入成本和生产线平衡率为目标的简单作业机器人生产线工位机器人数量配置模型,具体模型如式(7) ~ 式(13)所示。
式 (7) 为模型的目标函数,即最小化机器人生产线并行作业机器人和备份机器人的投入总成本以及最大化生产线平衡率。本文通过在机器人投入成本前加入一个平衡率权重,将两个目标合并为一个目标函数。其中,机器人生产线上各工位并行作业机器人数量ni和备份机器人数量mi是该模型的决策变量。式 (8) 为机器人生产线的产能约束,即该机器人生产线瓶颈工位作业时间不能大于预设产能下的节拍时间。式 (9) 为机器人生产线平衡率计算公式。式 (10) 为各工位上并行作业机器人数量约束。当工位上并行作业机器人在整个生产过程中没有发生故障,或者发生故障时能够立刻被备份机器人替换,此时工位上完成产品所需要的并行作业的机器人数量最少,即并行作业机器人数量达到下限;反之,当工位上并行作业机器人出现故障且无法被备份机器人及时替换时,工位上需要的并行作业机器人数量最多,即并行作业机器人数量达到上限。式 (11)表示机器人生产线各工位上并行作业机器人的数量应当不少于备份机器人数量。式 (12) 和式 (13) 是模型完整性约束,分别表示对ni和mi进行非负整数约束以及各工位并行作业机器人单位投入成本要大于等于同工位上的备份机器人。
3 遗传算法设计
遗传算法起源于20 世纪60 年代初期,由密歇根大学Bagley 博士首次提出,在80 年代进入兴盛发展时期并被广泛运用于自动化控制、生产计划、机器学习、路径规划等研究领域。它通过迭代的方式进行选择、交叉以及变异等运算,交换种群中染色体的信息,最终得到符合要求的染色体,是一种鲁棒性较强的全局搜索算法[12]。本文模型的求解属于非线性规划问题,传统的非线性规划算法计算繁琐且精度较差,因此本文设计了合适的遗传算法来对问题进行求解,操作主体流程如图3 所示。

图3 遗传操作流程Figure 3 The flow chart of genetic algorithm
3.1 编码设计
本文的决策变量为机器人生产线上各工位并行作业机器人的数量ni和备份机器人数量mi,由于决策变量之间存在着较强的相互约束关系,因此本文选择整数编码的形式。其中,染色体奇数点位上的基因表示每个工位上并行作业的机器人数量,其取值范围可以通过式 (10) 得到,即 [min_ni,max_ni]。染色体偶数点位上的基因则表示每个工位上备份机器人的数量,其范围为 [0,ni]。而染色体的长度是固定的,代表的是生产线上的工位数量乘以2。如图4 所示,染色体xi=[n1,m1,n2,m2,n3,m3,n4,m4,n5,m5]=[2,0,1,1,1,1,2,1,3,1],映射到解空间表示的是机器人生产线上有5 个工位,对应各工位机器人数量配置方案为在第1 个工位上仅设置2 个并行作业机器人;在第2 个和第3 个工位上均设置1 个并行作业机器人,1 个备份机器人;第4 个工位设置2 个并行作业机器人和1 个备份机器人;第5 个工位设置3 个并行作业机器人和1 个备份机器人。

图4 染色体Figure 4 Chromosomes
3.2 种群适应度设计
适应度函数是用于区分群体中个体好坏的标准,是进行自然选择的唯一依据。本文是求目标函数F(x)=f{n,m} 的最小值,同时考虑到不同个体代入到目标函数中得到的函数值差距不大,因此将得到的每个目标函数值减去该种群最优目标函数值之后加上一个放缩因子,再对其值取倒数作为个体的适应度值。目标函数值越小的个体,适应度越大,个体越优,越容易被选择保留下来。
其中,f{n,m} 为 目标函数值, b est(f{m,n}) 为种群中最优目标函数值,q为放缩因子。
3.3 遗传算法操作步骤
1) 初始化种群。
利用随机方法生成如图4 染色体一样的符合约束要求的染色体个体组成初始的种群,其具体操作步骤如下所示。
步骤1通过式 (10) 求出在预设产能下,生产线上各工位作业机器人数量的上下界即 [min_ni,max_ni]。
步骤2通过随机函数在 [min_ni,max_ni]范围内生成各工位并行作业机器人的数量ni。由于工位上备份机器人设置的数量不会多于同工位并行作业机器人的数量,因此在 [0,ni]范围内生成各工位的备份机器人数量mi,并将其进行组合,构成一条染色体。
步骤3通过式 (8) 对随机生成的染色体是否满足工位作业时间约束进行判断。如果满足要求,则将该染色体保留并代入目标函数中,计算其对应的目标函数值;反之,则不予保留。
步骤4重复进行步骤2 和3。直到保留的染色体个体数量达到初始设定的种群规模sizepop,完成种群初始化。
2) 选择操作。
将染色体计算得到的目标函数值代入种群适应度公式 (14) 中,计算得到每条染色体对应的适应度值。然后依据种群中个体的适应度值大小,按照一定的规则进行选择,并保留一部分作为下一代种群的父代。本文采用简单易操作的轮盘赌选择法,其对个体进行选择的基本思想是个体被选择的概率与其适应度函数值大小成正比。个体被选择并遗传至下一代的概率为
交叉操作是指从种群中随机选择两个个体作为父代染色体,通过父代染色体间交换部分基因,从而产生新的子代染色体。在交叉操作的过程中,父代染色体部分相关特征也通过交叉操作遗传给了新的子代染色体,在这里代表的则是生产线各工位上并行作业的机器人数量和备份机器人数量。由于各工位并行作业的机器人数量与备份机器人数量之间存在一定的约束关系,即染色体内部各基因之间存在着约束关系。因此,本文采用部分匹配交叉的方式进行交叉操作,具体步骤如下。
步骤1用随机函数生成一个随机数与交叉概率相比,若小于交叉概率则进行交叉操作;反之,则本次不进行,直接进入下一次交叉迭代。
步骤2利用随机函数生成两个随机数,确定种群中哪两条染色体进行交叉操作。
步骤3利用随机函数生成一个在 [1,l]范围内的随机数,以此确定染色体上进行交叉操作的基因位置为 { 2l-1,2l} ,即确定两个方案中哪个工位上的作业机器人和备份机器人数量进行交换。
步骤4将两条染色体对应位置上的基因进行相互交换,生成新的个体,计算新的染色体各工位的作业时间,并将其代入至式 (8) 中,判断是否满足生产线各工位作业时间约束。若满足,则保留新的染色体;否则重新回到步骤2,进行父代染色体的重新选择。父代染色体通过交叉操作产生符合要求的子代染色体的过程演示如图5 所示。
步骤5交叉迭代操作的次数达到种群规模数量sizepop,则结束交叉操作,进入到变异操作。
为因素集建立一个模糊子集K=(k1,k2…kn),其中ki表示每个因素集的因素在综合评价中的影响力,约束条件为{0≤ki≤1,∑ki=1}. 权重集K与模糊评价矩阵D进行模糊关系运算,得到驾驶员驾驶行为的模糊综合评判集F:
4) 变异操作。
为了增加种群的多样性,同时希望种群中个体向适应度高的方向变化,本文通过定位寻优的方法来对个体进行变异操作,具体的操作步骤如下所示。
步骤1利用随机函数生成一个随机小数与变异概率相比,若小于变异概率,则进行后续步骤2 的变异操作;反之,则本次不进行变异操作,直接进入下一次变异迭代。
步骤2通过随机函数在 [1,sizepop]范围内生成一个随机数pick,以确定当前种群中需要变异的个体,并将其作为父代染色体。然后通过随机函数在[1,l]范围内生一个随机数index,以此来确定个体变异对应的基因位置。
步骤3利用式 (16) 计算父代染色体2∗index-1基因位置上对应的并行作业机器人的数量ni当前处于什么位置。
步骤4若pw>0.5 , 则对染色体 2 ∗index 位置上的基因在 [0,nindex]范围内按从小到大的顺序进行取值,并依次对其进行工位作业时间约束检测,保留符合要求的最小基因个体进入下一次变异操作;若pw≤0.5, 则对染色体 2 ∗index-1 位置上的基因按从小到大的原则在 [min_nindex,nindex]进行依次取值,并进行工位时间约束检测,保留符合要求的最小基因个体进入下一次变异操作。
步骤5返回至步骤1,重复上述变异操作,直到变异迭代次数达到设置种群规模数量,则结束变异操作。具体的父代染色体通过变异操作产生新的个体过程,如图6 所示。
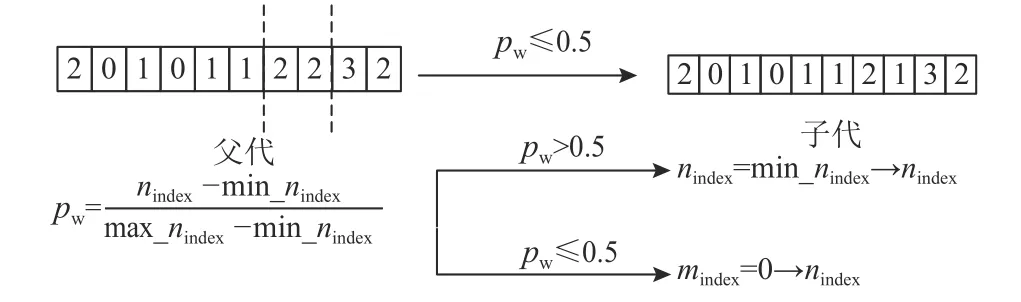
图6 变异操作图Figure 6 The mutation operation
5) 返回至选择操作,重复遗传算法迭代。
返回至选择操作,直到遗传迭代的次数达到设定的迭代次数maxgen,则结束遗传算法。此时种群中最优的个体对应的各工位工业机器人配置数量设置就是通过遗传算法得到的最优配置方案。
4 实例验证
4.1 背景介绍
以手机生产与组装一体化的M 公司为例,来说明如何在简单作业机器人生产线上进行工位冗余设计,以提升生产线生产的稳定性。由图7 可知,该生产线由5 个工位组成,每个工位上都安装了不同的工业机器人进行作业,分别负责锁螺丝、TP 点胶、TP 压合、耦合测试和自动写号等工序。为确定该条自动化手机装配生产线各工位上并行作业机器人和备份机器人的最优数量配置,本文通过查询并统计过往订单数据以及各工位上工业机器人的作业能力,得到该条自动化手机装配线的生产目标节拍时间为11 s/件。各个工位上工业机器人的正常作业时间、故障类型、故障概率以及对应的故障维修时间等参数详见表4 所示。

图7 自动化手机装配生产线部分工位生产情况Figure 7 Production of some workstations of an automated cell phone assembly line
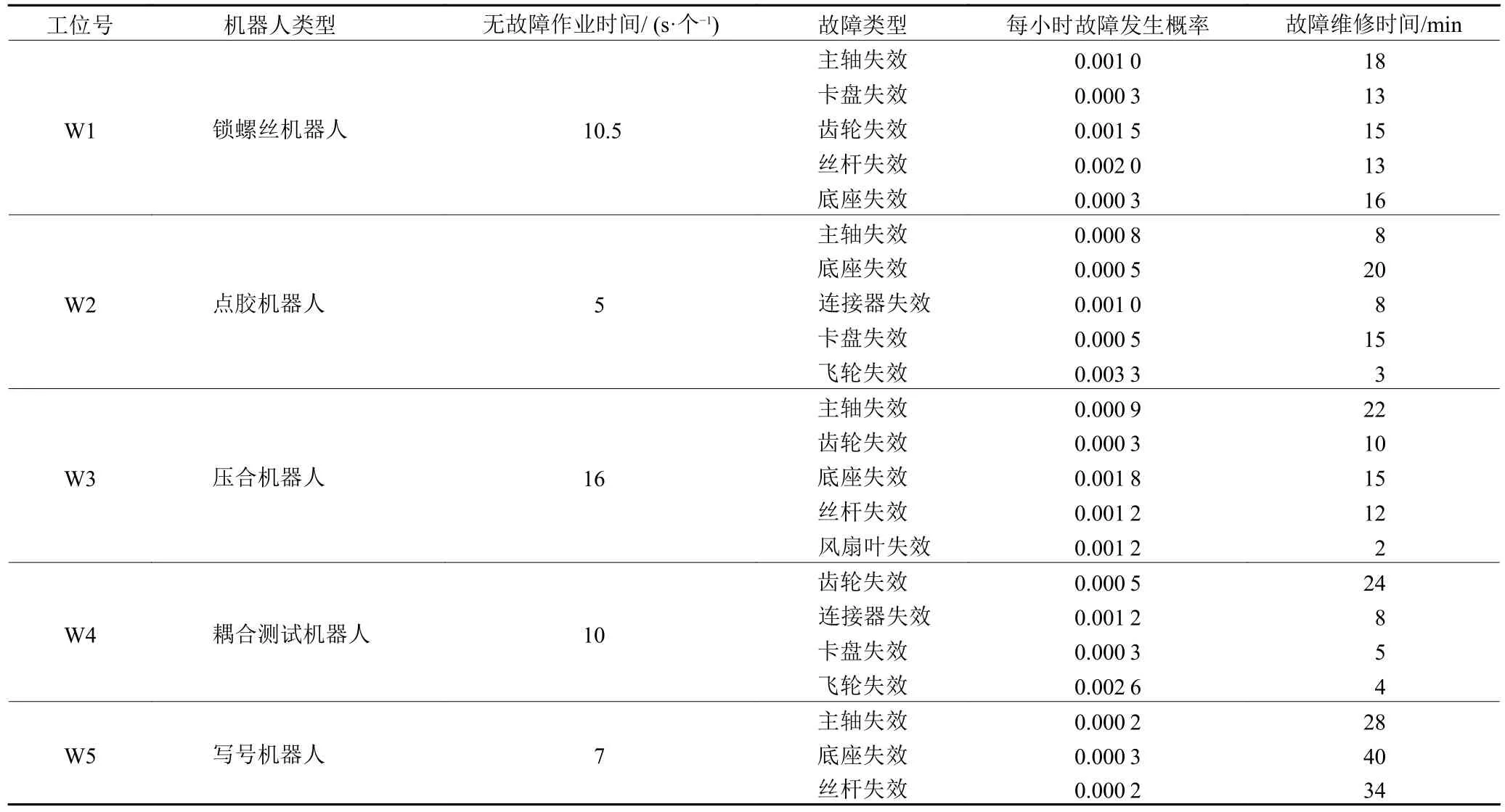
表4 各工位工业机器人具体参数Table 4 Specific parameters of industrial robots at each workstation
4.2 考虑故障影响的工业机器人标准工时计算
根据表4 中各工位工业机器人的故障类型以及对应的故障工时消耗数据,以W1 工位上的锁螺丝机器人为例,说明工业机器人标准工时的计算。由表4 可以得到,在工位W1 中,锁螺丝机器人无故障作业时间为10.5 s/个。但由于生产过程中锁螺丝机器人可能会出现主轴失效、卡盘失效、齿轮失效、丝杆失效、底座失效等故障,因此其实际平均完成一个零部件的时间要高于10.5 s/个。依照式 (4),将宽放系数设为0,可以计算得到在考虑机器人故障影响时,锁螺丝机器人完成零部件的标准工时为15 s/个,具体见式 (17)。
由此可以得到,W1 工位上的锁螺丝机器人的可靠性为R=T/t=0.7 。同样方法可以计算得到该手机装配线上其他工位工业机器人的作业情况,如表5所示。

表5 各工位工业机器人作业情况Table 5 Operation of industrial robots at each workstation
4.3 工位并行作业机器人和备份机器人数量配置确定
由表5 可知,该机器人生产线上共有5 个工位,通过标准工时测定方法测得各工位工业机器人无故障作业时间T=[10.5,5,16,10,7],在考虑故障影响下的各工位工业机器人标准工时t=[15,7.5,20,12,8.5],每个工位完成一件产品生产需要组装的零部件个数a=[2,4,2,1,3]。为求得在满足生产节拍时间要求下,以最小化工业机器人投入总成本和最大化生产线平衡率为目标时的各工位最优的并行作业机器人以及备份机器人数量配置,本文采用遗传算法对模型进行求解。
本案例中的决策变量为手机自动化装配线上各工位并行作业机器人数量和备份机器人数量。首先,通过式 (10) 计算出各工位上并行作业机器人数量的上下限,如表6 所示。在该范围内随机生成各工位上并行作业的机器人数量ni,然后在 [0,ni]范围内生成各工位上的备份机器人数量mi。最后判断是否满足瓶颈工位时间小于11 s/件的要求,从而生成符合要求的初始染色体种群。
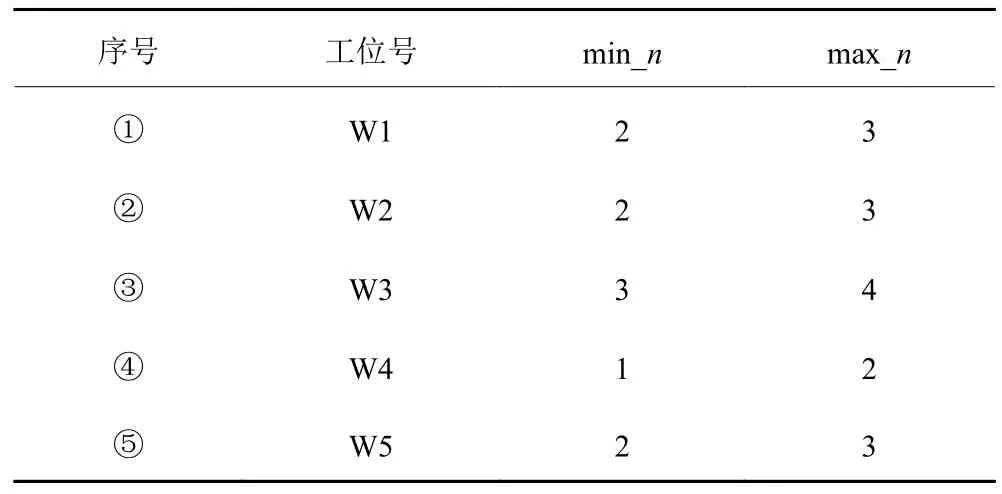
表6 工位并行作业机器人数量上下限Table 6 Upper and lower bounds of the number of parallel operating robots at workstations
在满足目标生产节拍时间Tmb=11 s/件 的条件下,通过第3 节中设计的遗传算法对各工位并行作业机器人以及备份机器人数量配置模型进行求解。其中,简单作业机器人生产线上的备份机器人所需投入成本相比于同类型的并行作业机器人要低。因此,本文将每个工位上备份机器人的单位成本设置为同类型并行作业机器人成本的0.8,即Ki′=0.8Ki,i=1,2,···,5。在Matlab R2019b 运行环境下,编写设计的遗传算法代码,并将迭代次数maxgen 设置为200,种群规模sizepop 设置为30,交叉概率pcross设置为0.8,变异概率pmutation 设置为0.2,适应度函数计算中的放缩因子q设置为0.01。通过多次运行遗传算法代码,得到图8 的运行结果,最优函数值为31.483 3。将算法输出结果与直接按照考虑故障因素影响的标准工时t配置各工位机器人数进行对比,得到如表7 所示的两种工位机器人数量配置方法结果对比。
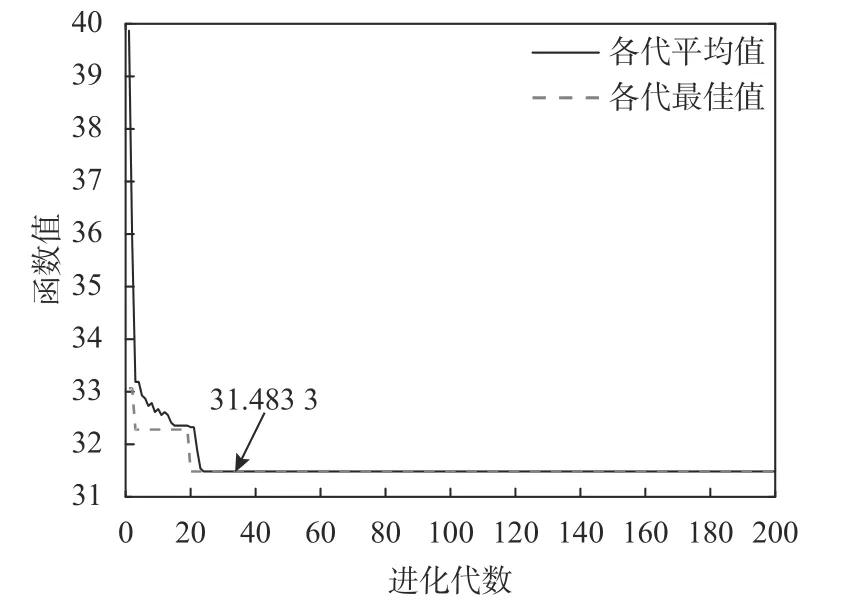
图8 遗传算法迭代结果Figure 8 Iteration results of genetic algorithm
由表7 可知,在目标产能Tmb=11 s/件 下,按照工位备份冗余方式配置各工位机器人数量时,各工位设置情况如下。在W1 和W2 工位上均分别设置2 个并行作业机器人参与作业,1 个备份机器人用于临时顶替故障并行作业机器人作业;在W3 工位上设置3 个并行作业机器人参与日常作业,设置1 个工业机器人用于充当备份机器人;在W4 和W5 工位上则分别设置1 个并行作业机器人和2 个并行作业机器人进行作业,即可达到生产目标要求。此时,该条手机自动化装配线瓶颈工位为W5 工位,瓶颈工位作业时间为10.9 s/件,生产线的平衡率为97.21%,所需要的工业机器人总投入成本为33.76 万元。与直接按照考虑故障因素影响的标准工时t设置工位并行作业机器人数量相比,生产线平衡率提升了9.22%,机器人总成本投入节约了9%。
5 结论
本文基于可靠性冗余设计原理和概率论相关知识,在考虑工业机器人故障情况下,分析工位上作业机器人和备份机器人搭配数量与工位工时之间的数量关系,构建了自动化生产线工位时间计算数学模型。最后在满足预设产能和装配线平衡的条件下,构建装配线工位工业机器人配置模型,并设计合适的遗传算法对问题进行求解。本研究为考虑机器人故障下的自动化生产线设计和优化管理提供了新的解决思路。但在实际生产下,工位备份机器人的设置会导致部分资源的浪费。因此后续研究将在此基础上对备份机器人功能由另一条生产线工位上的作业机器人充当的装配优化管理进行研究。
