时变时滞奇异复杂动态网络的间歇控制与同步
2024-01-16王维峰黄林梅俊
王维峰,黄林,梅俊
(中南民族大学 数学与统计学学院,武汉 430074)
近年来,复杂网络的同步问题成为热门的研究课题之一.复杂网络的同步是指,在不同的初始条件下,经过网络中节点的相互作用,节点的动态行为随着时间的推移而逐渐接近并最终达到相同的状态.同步问题的一个明显特征是,当前节点如何与整个网络中的其他节点进行通信,以便完成一个同步任务[1].
奇异系统又称为广义状态空间系统、描述符系统等.与传统的复杂网络相比,奇异复杂网络多了代数方程部分来描述节点的奇异动态行为.因此,奇异复杂网络具有更强的实用性.例如,有限的通信资源要分配给不同级别的用户,在资源的分配过程中,需要构造具有约束条件的复杂网络模型来实现资源的有效分配[2].另外,在复杂网络中,如果节点之间相互作用时出现了时变时滞现象,可能会极大地改变系统的动态行为[3],比如可能会改变系统的稳定性和遍历性.因此,为了更加准确地模拟实际网络,本文考虑了具有时变时滞的奇异复杂系统.
到目前为止,很多学者在具有时变时滞奇异复杂网络的同步领域上提出了一些控制方法,例如:事件触发通信机制[1]、线性反馈控制[2]和钉扎控制[4-5].同线性反馈控制和钉扎控制相比,间歇控制能够更有效地节约成本.事件触发控制需要连续或定期检测反馈控制变量,以验证变量是否满足事件触发条件[6].而间歇控制的工作原理是将时间区间分为控制区间和非控制区间,控制信号进入控制区间时工作,进入非控制区间时休息,所以间歇控制能够更加节约控制成本.因此,研究基于周期性间歇控制的时变时滞奇异复杂动态网络的指数同步具有重要的理论价值和实际意义.
基于上述因素,本文通过设计适当的周期性间歇控制器,以实现具有时变时滞的奇异复杂动态网络指数同步.由于经典的Lyapunov 函数不能很好地对奇异复杂动态网络进行稳定性分析,所以本文考虑了一种混合的Lyapunov 函数[7],结合Wirtinger 型积分不等式[1]和LMI理论[8],推导出基于周期性间歇控制的时变时滞奇异复杂动态网络指数同步的充分条件,进一步利用LMI 工具箱求解线性矩阵不等式,并通过数值仿真验证结论的有效性.
1 模型描述与知识准备
考虑以下由N个具有时变时滞的耦合节点组成的奇异复杂动态网络,其中第i个节点的动力学方程描述如下:
为简单起见,本文将模型称为驱动系统,并且构建对应的响应系统如下:
其中:E为n阶奇异矩阵,即rank(E)=r<n;xi(t)∈Rn,yi(t) ∈Rn是节点i的状态向量;φi(θ)和φi(θ)分别是驱动系统和响应系统在节点i的初值条件,ui(t)是控制输入:Rn× R →Rn为一个非线性连续可微向量函数;Γk=diag(γk1,γk2,…,γkn)为内耦合矩阵;ck表示节点i,j之间的耦合强度,k=1,2.定义矩阵D={dij}N×N为耦合构型矩阵:如果节点i与节点j(i≠j)之间有联系,则dij=dji=1;否则dij=dji=0,D的对角元素为定义函数τ(t)为时变时滞.
定义同步误差ei(t)=yi(t)-xi(t),i=1,2,…,N.联立模型,可以得到下述误差动态系统:
因此,驱动系统与响应系统的之间的同步问题等价为误差动态系统的稳定问题.
设计节点i(i=1,2,…,N)的周期性间歇控制器:
其中:Ki∈Rn×n为节点i的增益矩阵,T是控制周期,δ是控制区间的长度.
定义 1[9]对于驱动系统和响应系统,若存在正常数k,N,使得误差系统的所有解ei(t)满足:
则驱动系统和响应系统实现指数同步,其中k为指数同步率
假设 1[10]假设时变时滞τ(t)及其导数(t)有界,且
假设 2[3]假设(·)是扇区有界非线性的,即对任意向量x,y∈Rn,有:
其中F1,F2为n阶常数矩阵,并且F1-F2>0.
引理 1[1]对于任意常数正定矩阵Z∈Rn×n,标量α>0,b>a,及函数向量x(·) ∈C([a,b],Rn),有下述不等式成立:
引理 2[3]设a∈R,A,B,C,D为适当维度的矩阵,克罗内积具有以下性质:
引理 3[11]设Y和Z是具有适当维度的实矩阵,则存在一个正常数ς,使得:
2 主要结果
在本节中,将通过周期性间歇控制方法分析具有时变时滞的奇异复杂动态网络的指数同步问题,并给出驱动系统与响应系统的指数同步性准则.
将误差系统写成克罗内积形式:
定理 1假设存在自由权矩阵Nj,Tj∈Rn×n(j=1,2)和n阶正定矩阵P,Q,R,Z,以及标量α1>0,α2>0,ς>0,λ<0,使得下面的矩阵不等式成立,则误差系统实现指数同步.
其中:ETP=PE ≥0,Q>0,R>0,Z>0.
当t∈ [nT,nT+δ),n∈N,V1(e(t),t)沿误差系统的轨迹关于时间t求导:
接下来将分析Lyapunov-Krasosvkii 泛函V(t)的上界.对于任何n∈N,
当t∈)[nT,nT+δ,联立(25)式和(31)式,可得:
假设存在常数ν满足0 <ν≤min{λmin(P1E),λmin(P2E)},使得下述条件成立:
另一方面,从Lyapunov-Krasosvkii 泛函V(t)的构造中,可以推出:
综上所述,由(34)~(36)式,可得:
因此,根据定义1,误差系统是指数稳定的.即在周期性间歇控制器下,驱动系统与响应系统实现指数同步.
证毕.
由于定理1的条件不是以线性矩阵不等式的形式存在的,所以节点i控制增益矩阵Ki不能用LMI工具箱直接求解.接下来,将对定理1中的矩阵不等式进行线性化,并得到以下基于LMI 的指数同步条件.
定理 2对于误差系统,假设存在矩阵Gj∈Rn×n,Mj∈Rn×n(j=1,2),Vi∈Rn×n,和n阶正定矩阵L,,以及标量η1>0,η2>0,ς><0,使得下述线性矩阵不等式成立,则误差系统实现指数同步,并且节点i的增益矩阵为Ki=ViP,i=1,2,…,N.
由(14)式和(15)式可知,Ω22<0,Θ22<0,则sym{(IN⊗T2)}和sym{(IN⊗N2)}是负定的,因此(IN⊗T2)和(IN⊗N2)可逆.设:
证毕.
3 数值仿真
考虑如下由6个耦合节点构成的具有时变时滞的奇异复杂动态网络,对于驱动系统和响应系统,其中的参数如下:
对于给定参数:τ(t)=0.08+0.02sin(t),c1=0.2,c2=0.1,T=0.2,δ=0.16.利用MATLAB 的LMI工具箱求解定理2 中的线性矩阵不等式,得到如下控制增益矩阵:
设驱动系统(1)和响应系统(2)的初值为:
在周期性间歇控制器(4)的作用下,图1 和图2分别描述了误差系统(3)的状态向量分量ei1(t)和ei2(t)(i=1,2,…,6)的运动轨迹.可以看出误差系统的状态变量随着时间的增加快速地趋于零点,即:驱动系统与响应系统实现指数同步,这证实了定理1的结论是有效的.
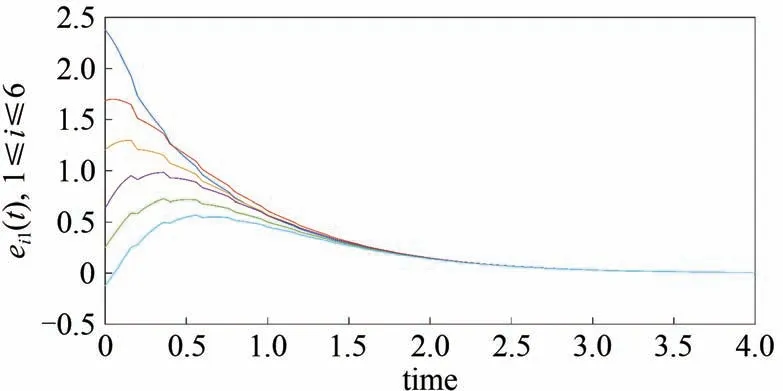
图1 同步误差分量ei1(t)(i=1,2,…,6)的运动轨迹图Fig.1 Motion trajectory diagram of synchronous error component ei1(t)(i=1,2,…,6)
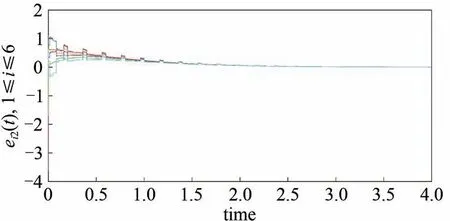
图2 同步误差分量ei2(t)(i=1,2,…,6)的运动轨迹图Fig.2 Motion trajectory diagram of synchronous error component ei2(t)(i=1,2,…,6)
图3 和图4 分别描绘了周期性时间触发控制器ui(t)(i=1,2,…,6)的轨迹图,图中纵坐标的值不等于0时,对应的时间区间是控制区间;如果纵坐标的值等于0时,对应的时间区间为非控制区间.
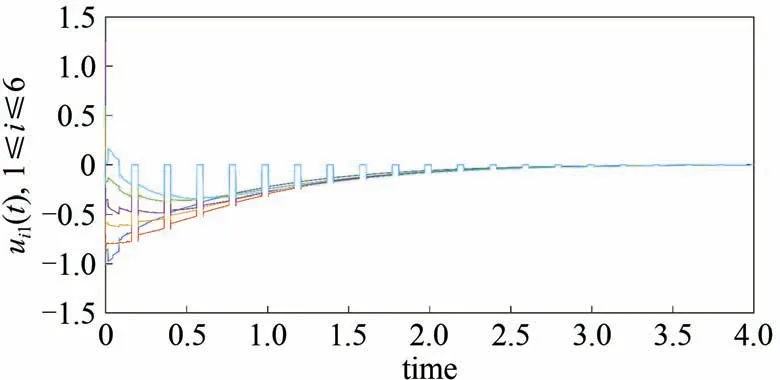
图3 周期性间歇控制器分量ui1(t)(i=1,2,…,6)的轨迹图Fig.3 Trajectory diagram of the periodic intermittent controller component ui1(t)(i=1,2,…,6)
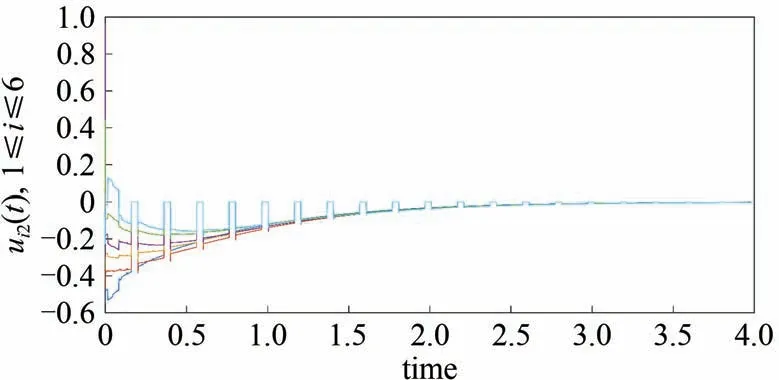
图4 周期性间歇控制器分量ui2(t)(i=1,2,…,6)的轨迹图Fig.4 Trajectory diagram of the periodic intermittent controller component ui2(t)(i=1,2,…,6)
4 结语
针对具有时变时滞的奇异复杂动态网络的指数同步问题,已有文献大都采用事件触发控制、钉扎控制和线性反馈控制方法.本文采用了一种新的方法,即通过设计周期性间歇控制器,使奇异复杂动态网络实现了指数同步,再利用Lyapunov-Krasosvkii稳定性理论,得到了具有时变时滞的奇异复杂动态网络指数同步的稳定性准则,数值模拟验证了结论的有效性.
