基于机器学习方法的贵阳雾预报模型研究

何东坡 , 王玥彤 , 杜小玲* , 周文钰 , 齐大鹏

（1.贵州省气象台，贵阳 550002；2.贵州省气候中心，贵阳 550002）

引 言

雾是一种能见度较低的天气现象，其中，浓雾天气不仅严重影响航空、公路、电力等安全运行，还会与污染物颗粒和有毒杂质结合对人体健康造成危害[1-4]。长期以来，对雾的预报，国内主要采用天气图分析、多元回归模型、模糊识别、数值模式等方法，但其业务应用效果均不够理想，迄今尚无较好的预报雾的客观产品[5-8]。为此，气象工作者针对雾的客观预报方法作了大量的探索和研究。王丽娟等[9]利用微波辐射计资料开展研究，指出强浓雾的发展过程分为浓雾形成、发展增强、消亡三个阶段，近地面逆温是浓雾产生的重要条件。王明等[10]基于FY-4A 卫星AGRI 高时空分辨率多通道数据开展夜间浓雾的识别研究，并对该识别方法在高速公路服务应用中的潜力进行了评估。刘红武等[11]采用概率密度匹配结合要素的方法对低能见度进行预报订正，其效果要优于仅使用概率匹配的订正方法。王楠[12]基于EC细网格产品，分析了影响能见度的主要因子，并提取与低能见度相关性高的物理量作为预报因子，构建了乌鲁木齐机场未来21 h 能见度预报模型。另外，周斌斌等[13]、滕华超[14]还基于集合预报技术提出了浓雾预报思路。

近年来，人工智能技术在气象领域得到了广泛应用，尤其是机器学习被更多地应用在气象预报方面。例如，Zhang 等[15-16]运用C5.0、CART 算法建立了热带气旋路径、强度的预报模型。李文娟等[17]基于数值预报和随机森林算法研发了浙江省强对流天气分类预报技术。陈晓平等[18]以雷达回波强度数据为基础，应用随机森林模型、BP 神经网络模型、卷积神经网络建立降雨量的预报模型。苗春生等[19]基于长江中下游夏季降水的前期春季影响因子，利用C5.0 算法构建了预报模型。陈贝等[20]利用指标判断法和非线性统计支持向量机法，分别对成乐路沿线各站大雾和能见度量级进行预报模型构建，最后通过人为经验订正对沿线各站大雾做出精细化客观预报。此外，苗开超等[21]、王月琴等[22]还将机器学习方法应用于浓雾、团雾的预报。

贵州省位于青藏高原向我国东部丘陵地区过渡的斜坡地带，其境内喀斯特地貌使得各地气候差异较大、天气变化复杂，是气象灾害多发省份之一。其中，大雾天气在贵州出现频率较高，是当地社会公众较为关注的灾害性天气之一，雾的监测和预报也是气象部门业务工作的重点之一。为此，本文以贵阳站“是否出雾”、“是否浓雾”的建模过程为例，首先归纳整理出包括气温、湿度、风速、气压、地温等11 个影响雾形成的主要气象因子，然后利用机器学习中的C5.0、CART、神经网络算法构建贵阳站的雾、浓雾预报模型，并检验评估各种算法模型的有效性，旨在为提高贵阳地区雾、浓雾预报水平提供科技支撑。

1 资料与方法

1.1 研究资料

雾是近地面大气中悬浮水滴或冰晶微粒导致的水平能见度低至1000 m 以下的天气现象[23]。根据雾对能见度的影响，将其分为3 个等级：（1） 雾，能见度0.5～1 km；（2） 浓雾，能见度0.05～0.5 km；（3）强浓雾，能见度小于0.05 km。本研究使用的资料为2015—2018年秋冬季贵阳国家气象站逐时观测数据，并整合为3 h数据集对雾、浓雾进行研究，观测要素包括海平面气压、2 m 气温、2 m 相对湿度、过去3 h 降水量、5 cm地温、15 cm 地温、3 h 变压、2 m 露点温度、水汽压、10 min 平均风速、10 cm 地温。根据上述雾的划分等级，分析3 h 数据集可知，雾出现次数为108 次，浓雾出现次数为236 次。观测要素均取3 h 平均值与能见度对应形成一条建模样本，本文共收集3862 条样本进行建模研究（当3 h 内同时出现雾和浓雾时，选取浓雾的能见度数值为样本值）。此外，因探空数据每天只有08 和20 时次，与样本时效不匹配，本文暂未将探空要素加入研究。

1.2 研究方法

本文主要选取了机器学习中决策树（C5.0、CART）和神经网络（多层感知器）算法，分别构建了贵阳站雾、浓雾的预报模型，并对预报效果进行检验评估，对比3 种算法的优缺点，挑选出贵阳站雾、浓雾的最优预报模型。具体介绍如下：

（1） C5.0 算法和CART 算法。这两种算法是决策树算法中使用较多的分类模型预报方法，决策树的建立是通过因子变量（雾的影响因子）将训练集样本进行不断拆分，每次拆分对应着一个因子和一个节点，将得到“差异”最大的两组分类（出雾或不出雾）。C5.0算法是根据信息熵递归构建决策树。设S为包含s个样本的数据集，Ci(i=1,2,3···,m) 为样本的m个分类，si是属于类Ci的样本数量。通过属性A将数据集S进行 划 分{S1,S2,···,Sω}(设 属 性A有 ω个 不 同 的值)，信息熵计算公式为：

CART 算法是对离散或连续依赖变量进行分类的非参数统计学方法。雾、浓雾预报模型的目标变量是离散型，适合建立分类决策树模型。CART 算法的分类准则为基尼不纯度标准和目标二分准则。将是否出雾、是否出浓雾作为两个二元分类。给定一个节点t，类概率p(j|t)表示该节点属于类j(j= 1,2,3,···,n)的几率。不纯度函数为：

由于本文只对是否出雾、是否出浓雾进行研究，为二元分类问题，公式（2）可简化为：

（2）多层感知器（Multilayer Perceptron，MLP）是神经网络中适合应用在分类预报问题的算法之一。MLP算法的结构分为3 部分：最底层为输入层，中间可以有多个隐藏层，最简单的MLP 只含一个隐藏层，最后为输出层。输入层即输入一个n维向量，有n个神经元（本文将把影响因子作为输入层）。隐藏层中假设输入层用向量X表示，则隐藏层的输出为f（W1X+b1）；其中W1是权重，b1是偏置，函数f可以是常用的sigmoid函数或者tanh 函数，隐藏层到输出层可以看成是一个分类的逻辑回归。本文输出层为是否出雾、是否出浓雾，即softmax 回归，所以输出层的输出为softmax（W2X1+b2），X1表示隐藏层(的输出f（(W(1X+b1)。ML))P) 计算公式为：

式中：G为softmax 函数。

（3）研究选用梯度下降法（Stochastic Gradient Descent，SGD）挑选最优化方案。具体步骤为：首先随机初始化所有参数，然后进行迭代训练，不断地计算梯度和更新参数，直到满足误差足够小且迭代次数足够多为止。

贵州省是我国唯一没有平原的省份，地形差异较大，呈“西高东低”的分布特点（图1）。因此，贵州省各地雾、浓雾的出现条件不尽相同，通常中西部及其他高海拔地区多锋面雾，东部和北部多辐射雾[8]，为更好地对雾和浓雾进行预报，需要对84 个国家气象站分别建模。因篇幅所限，本文仅以贵阳站为例进行影响因子分析和预报模型建立研究。

图1 贵州省地形与国家气象站分布

2 气象因子与能见度相关性分析

表1 给出了本文收集整理的11 个主要气象因子，图2 给出了贵阳站3 h 能见度数据与同期各气象因子的相关关系。如图所示，海平面气压、3 h 变压、2 m相对湿度、过去3 h 降水量、10 min 平均风速与能见度呈负相关，其中海平面气压、2 m 相对湿度与能见度的相关性通过了95% 水平的显著性检验，即当海平面气压、3 h 变压、2 m 相对湿度、过去3 h 降水量、10 min 平均风速偏大（小）时，能见度偏低（高）；其余6 个因子与能见度均呈显著正相关，即当这6 个因子偏大（小）时，能见度偏高（低）。

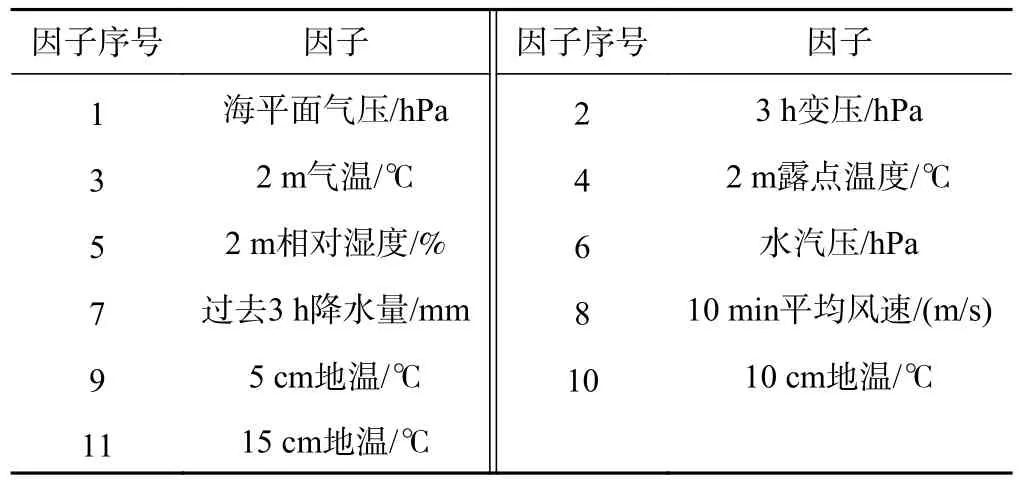
表1 影响能见度的11 个气象因子

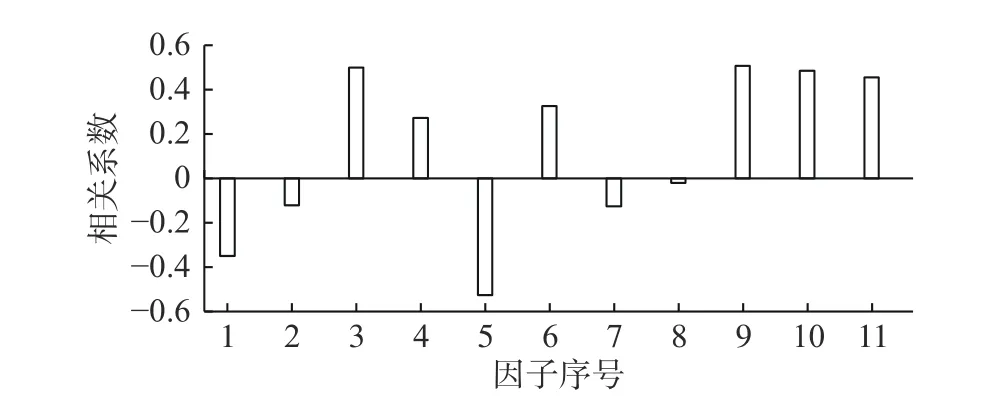
图2 贵阳站能见度与11 个气象因子的相关关系

可见，上述这11 个气象因子均对能见度有着一定的影响，其中海平面气压、2 m 气温、2 m 露点温度、2 m相对湿度、水汽压、5 cm 地温、10 cm 地温、15 cm 地温与能见度呈显著性相关，而仅根据某个因子对能见度进行预报，其准确率不能达到业务需求。机器学习的特点就是在多个因子的影响下，通过大量快速的计算寻找最优的预报方法。因此，在算法建模时，综合考虑所有相关因子，根据多个因子组成的判别规则来进行雾、浓雾预报。下节将基于这11 个气象因子，利用机器学习中的C5.0、CART、神经网络算法，分别建立贵阳站雾、浓雾预报模型。

3 基于机器学习方法的雾、浓雾预报模型建立与检验

3.1 基于决策树算法（C5.0、CART）预报模型

从整理的贵阳站3 h 数据（共3862 条样本，46344数据量）中，随机选取80%左右的样本数据作为预报模型的训练集来用于预报模型的建立，再利用剩余20%左右的样本数据作为预报模型的检验集，对模型预报准确率进行检验。利用表1 中11 个气象因子作为能见度预报模型的输入变量，“是否出雾”作为预报模型的目标变量，以能见度小于1 km 作为出雾指标。通过多次随机选取训练集和检验集，对11 个气象因子进行筛选与分析，并建立多层次分支框架预报模型，再对模型进行预报检验，最终选取最简捷且检验准确率最高的模型作为贵阳站“是否出雾”预报模型。

首先利用C5.0 算法，经过多次训练建模、合理剪枝和检验，得到了贵阳站“是否出雾”的最优预报模型（图3）。如图所示，最终参与模型建立的气象因子有2 m 相对湿度、2 m 气温、海平面气压、15 cm 地温，而为了防止过度拟合，其它气象因子被剪枝处理。图3 中节点0 为根节点，即显示训练集样本总数，节点1、3、6、7、8 为叶节点，即通过气象因子无法再往下分类。每条从根节点到叶节点的路径为一条预报规则，模型共得到了5 条判别是否出雾的规则。叶节点中如果“T”为深色，则表示该叶节点判别结果为出雾（能见度＜1 km）；如果“F”为深色，则表示该叶节点判别结果为不出雾（能见度≥1 km）。例如，节点6 中“T”为深色，即从节点0 到节点6 这条路径规则的判别结果为出雾，该节点正确分类样本数为192，错误分类样本数为69。从图3 中可以看到，参与建模的4 个气象因子中，以2 m 相对湿度的权重最大。从节点1 中分类情况可知，节点1“F”为深色，即为不出雾，大量的能见度≥1 km 数据集被正确分到了节点1 中，节点2 中出雾与不出雾的数据均有。因此，只考虑2 m相对湿度小于97% 来判别，即可预报出大量不出雾的情况，但是用2 m 相对湿度大于97%来预报出雾的准确率偏低，只有从根节点到叶节点的完整判别路径才能更好地对出雾、不出雾进行预报。

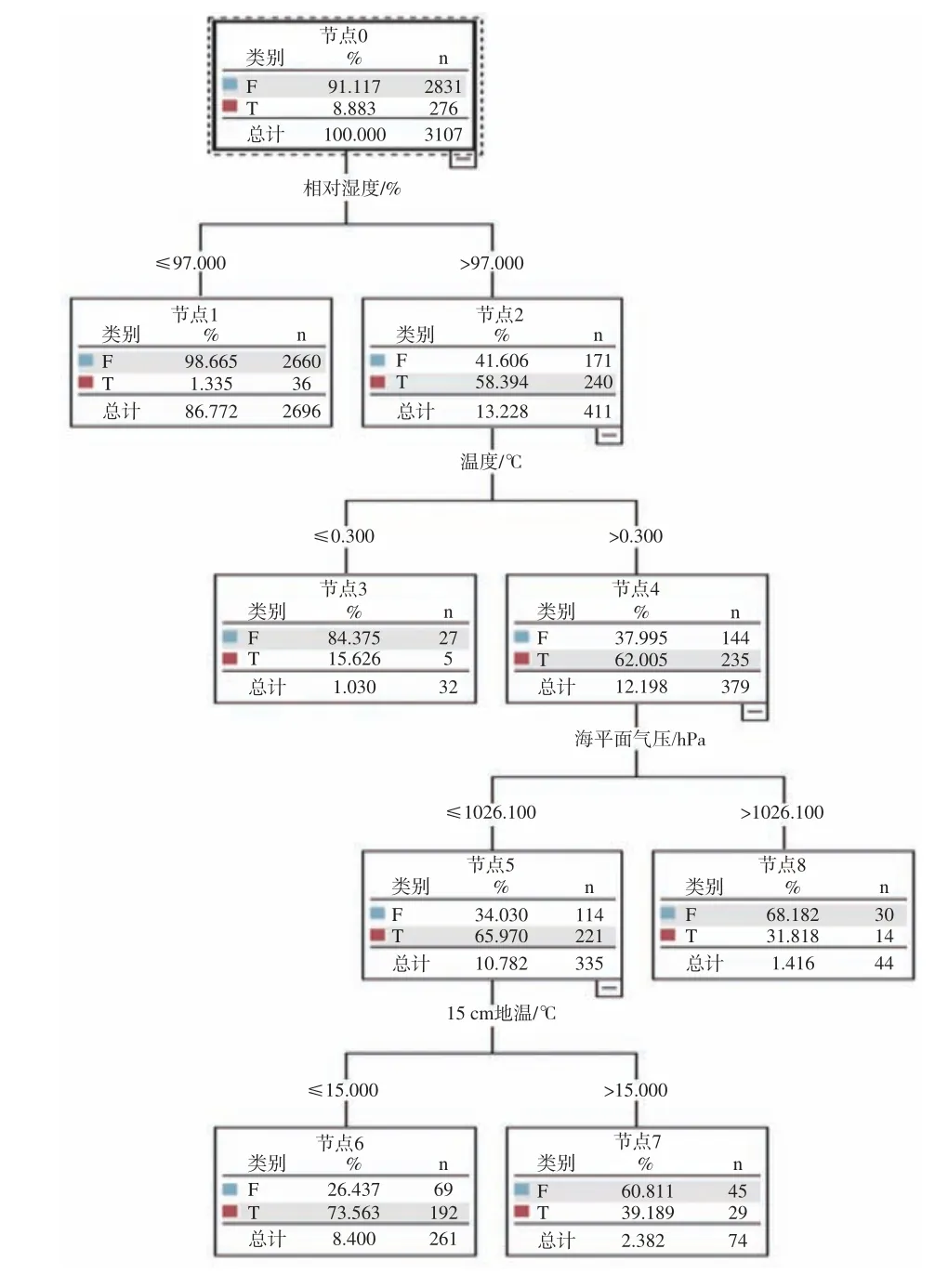
图3 基于C5.0 算法的贵阳站“是否出雾”预报模型

表2 给出了基于C5.0 算法的贵阳站“是否出雾”预报模型规则集。如表所示，第一列为“If-then”形式的判别规则，第二列为参与建立每条规则的属性变量，第三列为每条规则的判别准确率，即每个叶节点中正确分类的样本数占该节点总样本数的比值。其中，判别出雾的规则有1 条，准确率为73.6%；判别不出雾的规则有4 条，准确率按表格顺序从上到下依次为98.7%、84.4%、75%、60.8%。由训练集获得的“是否出雾”预报模型准确率达95.37%，再运用剩余未参加建模的20%能见度和气象因子样本数据对模型进行预报效果验证，检验准确率达92.98%。可见，C5.0 算法在贵阳站“是否出雾”预报中得到了较好的应用，训练集和检验集准确率均高达90% 以上，为雾的预报提供了新思路和新方法。

表2 基于C5.0 算法的贵阳站“是否出雾”预报模型规则集

CART 算法在父节点利用基尼系数递归随机测试变量和分割阈值，直到产生最优的测试变量和分割阈值，进入到子节点后继续父节点的行为直到满足结束条件。建模过程中，父分支最小记录数为训练样本的2%，子分支最小记录数为训练样本的1%，使用Gini杂质测量对记录进行分类，过度拟合防止集合取30%。通过多次训练建模与模型检验，得到了准确率最高的贵阳站能见度预报模型（图略），模型结构与C5.0 算法模型相似，从根节点到叶节点模型一共有4 条判别规则（表3）。其中，判别贵阳站出雾的规则有1 条，判别规则准确率为72.2%；判别不出雾的规则有3 条，准确率按表格顺序从上到下依次为98.2%、73.9%、58.6%。由训练集获得的“是否出雾”预报模型准确率达94.42%，再运用剩余未参加建模的样本数据对模型进行预报效果检验，检验集准确率高达到95.87%。

表3 同表2，但为CART 算法

综上可知，C5.0 和CART 两种算法构建的模型在贵阳站“是否出雾”预报中均有较为优良的表现，其检验准确率均在90% 以上，可以较好地为判别贵阳站“是否出雾”提供科学参考。但从两个算法的规则集中可以看出，C5.0 算法对出雾的预报准确率略高于CART 算法，而在模型整体预报能力中CART 算法要优于C5.0 算法。

3.2 基于神经网络算法（MLP）预报模型

利用神经网络中的MLP 算法对贵阳站“是否出雾”进行建模，停止规则以“无法进一步降低误差”为标准，激活隐藏层运用tanh 函数（sigmoid 函数应用效果不佳），激活输出层运用Softmax 函数。同样从整理的贵阳站3 h 数据中随机选取80%左右的样本数据作为预报模型的训练集，剩余20% 左右的样本数据作为预报模型的检验集来检验有效性。利用表1中11 个气象因子作为预报模型的输入变量，“是否出雾”作为预报模型的目标变量，以能见度＜1 km 作为出雾指标。通过大量的反复训练，最终获得的神经网络“是否出雾”预报模型准确率达94.2%，再运用剩余未参加建模的20% 样本数据对模型进行检验，准确率高达93.94%。参与建模气象因子中，2 m 相对湿度对能见度的影响占比最大（28%），其次是15 cm 地温（占14%），最小的是10 cm 地温（3%）。

通过上述研究发现，机器学习中的C5.0、CART和神经网络算法在贵阳站“是否出雾”预报中均表现出较好的应用效果，模型检验准确率均在90%以上。以相同的思路对贵阳站“是否出浓雾”建立了3 种算法的预报模型（判别指标为能见度＜0.5 km），分析可知：C5.0 算法模型的训练集准确率为97.71%，模型检验准确率为97.77%；CART 算法模型的训练集准确率为95.94%，模型检验准确率为94.49%；神经网络算法模型的训练集准确率为95.16%，模型检验准确率为95.67%。图4 给出了3 种算法构建的贵阳站“是否出浓雾”预测模型的评估结果。如图4a 所示，在C5.0算法检验集中，数据样本增加到16% 以后的收益高于90%；如图4b 所示，在CART 算法检验集中，数据样本增加到18%以后的收益高于90%；如图4c 所示，在神经网络算法检验集中，数据样本增加到18%以后的收益高于90%，而增加到20%以后的收益达到100%。由此可见，C5.0 算法和神经网络算法在贵阳站“是否出浓雾”预报中效果更好，且神经网络算法收益效率更高。但需要注意的是，各模型的出雾、出浓雾TS评分、空报率、漏报率分别介于0.41～0.56、0.25～0.27、0.23～0.25，尤其是空报率和漏报率还有待改进。

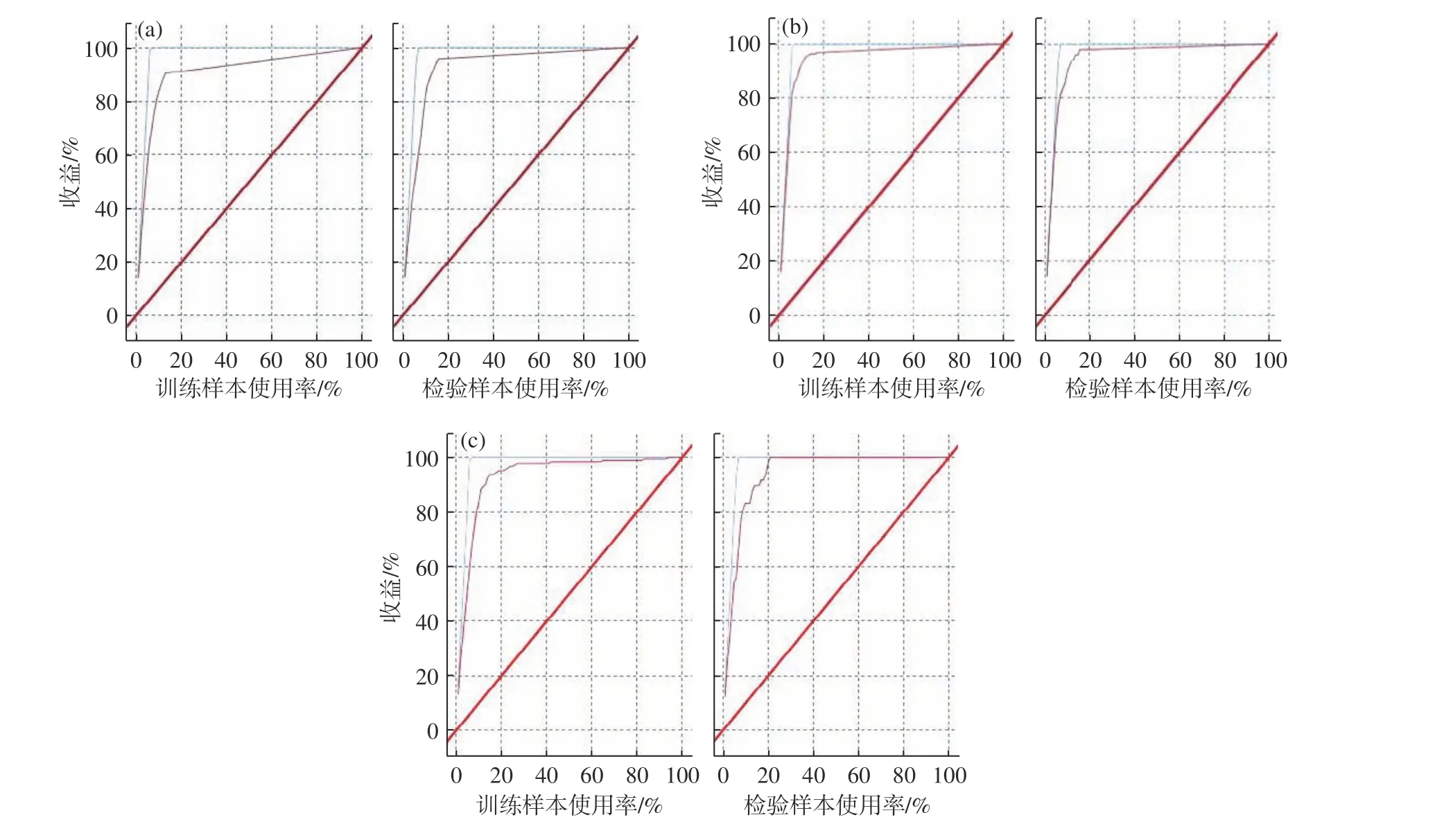
图4 3 种算法的贵阳站“是否出浓雾”预报模型评估（a.C5.0，b.CART，c.神经网络，粗红线为基线，细红线为累计散点，蓝线为最佳线）

本文建立的雾、浓雾预报模型在业务应用中需要将模式数据（CMA、EC）带入模型中，最终给出是否出雾、是否出浓雾的预报结果，理论上预报时效可以和模式数据的预报时效匹配，但是模式本身就有误差，且时效越长，误差越大。因此，上述雾、浓雾预报模型在业务应用中随着预报时效增加，准确率也将逐渐降低。

3 结论与讨论

本文利用机器学习中的C5.0、CART、神经网络算法分别对贵阳站“是否出雾”、“是否出浓雾”建立了预报模型并进行检验评估，得到如下主要结论：

（1）C5.0、CART、神经网络算法在贵阳站雾的预报中均具有较高的应用价值，“是否出雾”模型训练准确率依次为95.37%、94.42%、94.2%，“是否出浓雾”模型训练准确率依次为97.71%、95.94%、95.16%。

（2）C5.0、CART、神经网络算法构建的预测模型检验准确率均在90%以上，“是否出雾”模型检验准确率依次为92.98%、95.87%、93.94%，“是否出浓雾”模型检验准确率依次为97.77%、94.49%、95.67%。各模型的出雾、出浓雾TS 评分、空报率、漏报率分别介于0.41～0.56、0.25～0.27、0.23～0.25，尤其是空报率和漏报率还有待改进。

（3）基于CART 算法建立的预报模型对于雾的预报效果更好，基于C5.0 算法和MLP 算法建立的预报模型对于浓雾的预报效果更佳，且MLP 算法模型的收益效率最高。

可见，机器学习方法在雾的预报中有较好的应用前景，能够建立准确率较高的预报模型，为业务工作中提供一种雾、浓雾预报的参考方案。此外，本文通过初步试报发现，预报模型的准确率比EC 能见度产品有所提升，但是空报率和漏报率较高。究其原因，可能是选取的影响因子还不够全面，而且在业务应用中还对模式产品的稳定性有所依赖。后续将选取更多的气象影响因子，并运用多种机器学习、深度学习方法研究贵州省能见度预报方法与应用。