高低指数环流不连续性周期振荡的物理机制研究

刘 春 , 孙 俊 , 白志娜 , 彭俊凯 , 于 涵

（1.辽宁省辽阳市气象局，辽阳 111010；2.四川省气象灾害防御技术中心，成都 610072；3.辽宁省盘锦市气象局，盘锦 124010；4.沈阳农业大学土地与环境学院，沈阳 110866）

引 言

指数循环是对流层西风环流变化中最典型的特征现象，关于它的研究起源很早。20 世纪30 年代末期，Rossby[1]就提出了西风指数的概念，即利用北半球35°N 和55°N 两个纬圈的气压梯度表示西风环流的强度，研究发现5 天平均的西风指数和平均海平面气压图上的大气活动中心（阿留申低压）的经度位置及其范围有很好的统计关系。此后，多项研究[2-6]进一步利用高空资料对指数循环的观测事实作了详细分析。

现在，指数循环现象主要是指对流层中层大范围流型的一种周期变化，表现为两种流型的交替变动：一种是高指数的纬向西风环流体系，其特征是纬向气流强，而行星波振幅小；另一种是低指数的经向西风环流体系，其特征是纬向气流弱，行星波振幅大，表现为阻塞形势发展和维持。高低指数环流形成约为2—6 周的周期性振荡，但是两种流型的交换常有“跳跃”性质，即具有不连续特征，是西风环流的最基本问题之一。

由于非线性动力学的发展，对西风环流高低指数不连续循环的研究较多。朱抱真和王斌[7]把Pedlosky[8]的弱非线性斜压不稳定理论用于分析超长波和基本西风的不稳定性，讨论了指数循环的过程。金飞飞和朱抱真[9-10]采用安德罗诺夫[11]的不连续振荡理论讨论了高低指数不连续性循环，研究指出：如果临界切变相对于热力强迫是次共振时，热力强迫波具有大振幅特征，构成低指数型环流；如果临界切变相对于热力强迫而言远超共振时，热力强迫波具有小振幅特征，构成高指数型环流。从动力学观点看，高低指数环流的转换过程背后，必然是大气方程的分歧在起作用。为此，刘春等[12]采用无穷维Euler-Lagrange理论分析了高低指数环流转换的分歧作用，研究认为：存在一个临界参数，当切变参数的绝对值超过这个临界参数，正压剪切流将分歧出阻塞流型，这意味着阻塞高压的形成；反之，当切变参数的绝对值小于这个临界参数，阻塞流型将恢复到剪切流，这意味着阻塞高压的崩溃；在切变参数变换的过程中，高指数环流和低指数环流形成了一个不连续性循环。

目前，已有研究较好地刻画了高低指数环流不连续性周期振荡的某些特征，如不连续性、振荡周期等，但这些成果在高指数的纬向气流和低指数的具有阻塞形势的经向环流等方面缺乏细致分析。因此，有必要做进一步研究。自Stuart[13]提出弱非线性理论以来，这一理论就被认为是研究流动稳定性最有效的方法之一，其基本思路是对非线性流动中待解物理量以小参数的幂级数展开，并对小参数的每一阶求解。一般而言，在解的高阶项上，将保留原方程的非线性特征，故称为弱非线性理论。Pedlosky[8,14-17]在Charney 等[18-21]的线性斜压不稳定理论的基础上，结合弱非线性理论和多时间尺度变换，解决了线性模式不能解释大气中存在较大波动和涡旋的问题。鉴于高低指数转换的不连续性及低指数的阻塞形势均具有典型的非线性特征，因此本文采用Pedlosky[8]提出的非线性方法，研究在一定的垂直切变条件下，当西风环流在没有外源强迫作用时，通过自身的波与流的非线性作用，激发出具有不连续振荡特征的流型，该流型不仅可以刻画出高指数的纬向气流和低指数的具有阻塞形势的经向环流，还可以刻画两者之间的不连续性周期振荡。研究过程分为三步：首先利用两层斜压模式，通过弱非线性理论和多时间尺度变换，得到一个无外源强迫的斜压波振幅方程；然后，分析斜压波在一定的垂直切变条件下具有的不连续性循环特征；最后，结合两层模式的近似解，讨论高指数的纬向气流和低指数的具有阻塞形势的经向环流之间不连续性周期振荡的物理机制。

1 斜压模式的线性理论

指数循环是出现在北半球西风带的一种典型现象，其运动近似满足准地转平衡。因此，可用准地转涡度方程和热力学能量方程[22-23]描述如下：

式中： β为Rossby 参数，f0为中纬度地转参数，为静力稳定度参数。

根据已有研究[7,9-10]，西风环流的指数循环主要是由斜压不稳定引起的。因此，研究采用最简单的两层模式的铅直结构（图1），即将整个对流层分为上下两层，5 个等压面分别用标号0、1、2、3、4 表示。上层运动由写在等压面p1上的涡度方程来描写，下层运动由写在等压面p3上的涡度方程来描写，上下两层的运动通过写在等压面p2上的热力学能量方程建立起相互联系。

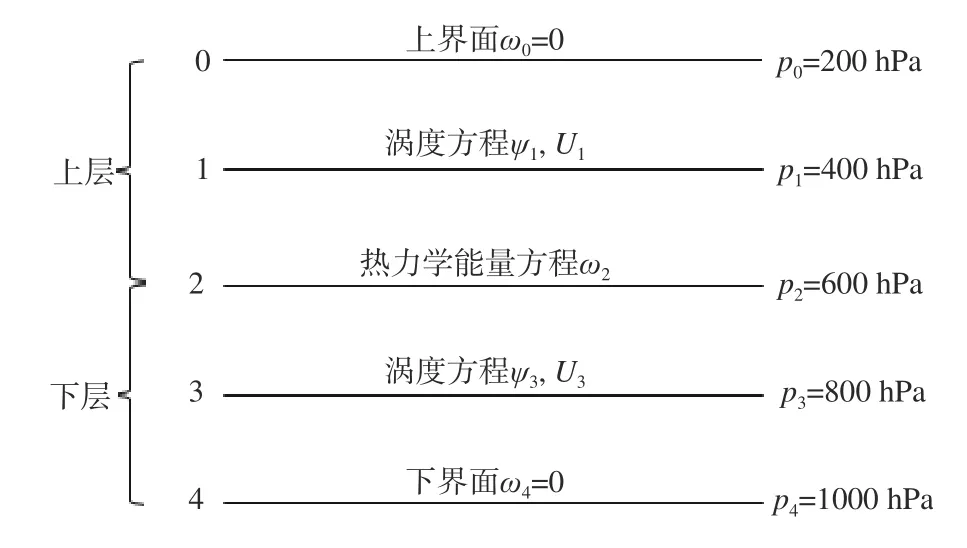
图1 两层模式的铅直结构

根据图1，可知方程组（1）的上下边界条件为

若各方程中对p的微商近似用差商代替[22]，则准地转斜压两层模式的闭合方程组（1）可以写为：

式 中： ψ2采 用 线 性 内 插 方 法 由 ψ1和 ψ3表 示，即ψ2=(ψ1+ψ3) 。可见，式（3）是关于未知变量 ψ1、ψ3、ω2的闭合方程组。

将方程（3c）带入到（3a）和（3b），消去 ω2，并做无量纲变换如下：

式中：L为纬向特征尺度，U为纬向特征速度。通过量纲变换，得到无量纲方程组如下：

为了叙述方便，将方程组（5）中的撇号去掉，得到方程组如下：

式中：无量纲参数 β=β′L2/U表征行星涡度特征，F=表征内旋Froude 数，H为铅直特征尺度。考虑通道流，有以下侧边界条件：

纬向流满足以下边界条件：

取准地转流为：

将式（9）带入到方程组（6）中，线性化处理为：

满足边界条件（7）和（8）的解形式可写为：

将解形式（11）带入到方程组（10）中，得到频散关系如下：

2 斜压模式的弱非线性理论

上节给出了描述指数循环的斜压模式，并简要阐述了它的线性不稳定性。根据弱非线性理论，必须选择参数作为幂级数展开的小参数。Pedlosky[8]在线性斜压理论的基础上，取垂直风切变的临界值Uc为基本态，垂直切变在基本态附近做微小变化，即为：

式中： |Δ|≪Uc～o(1) 。对＜2F的情形，有如下条件：

式中：ci为c的虚部。可见，当垂直切变比临界值增加Δ时，扰动增长率正比于 |Δ|1/2。为此，在初始线性不稳定阶段，其振幅增长率属于慢时间尺度[10-12]，即为：

因此，考虑双时间尺度变换[21]，即为：

取流函数为：

将变换（17）和流函数形式（18）带入到式（6）中，得到以下方程组：

将 φn展开如下：

将式（20）带入到方程组（19）中，得到各阶摄动问题。下面将对各阶摄动问题求解，在求解过程中，往往会遇到奇异项，根据摄动思想，需要通过限制条件将奇异项消除，使方程组（19）的解有意义。|Δ|1/2

（1） 阶问题

|Δ|1/2阶问题为线性问题，方程组（21）满足齐次刚性条件（7）和（8）的解可写为：

（2） |Δ|阶问题

将解（22）带入方程组（23）中，得到以下方程组：

方程组（24）中的非齐次项包括两类：一类是与x、t无关的，即前一项；另一类是与x、t相关的，且具有自由中性解结构。这两类强迫都可以强迫出自由波，其中前者强迫出纬向流（平方解），后者强迫的是中性波扰动。因此，都必须加以消除奇异条件的限制。在齐次边界条件（7）和（8）下，通过消除奇异条件，可以得到 |Δ|阶问题的解具有如下形式：

从上述分析可知，通过消除 |Δ|阶问题的奇异条件，并不能求出关于振幅A(T)的关系式。因此，为了求出A(T) 和Φ(y,T)(n=1,3)，需要进一步考虑更高阶的问题。

（3） |Δ|3/2阶问题

将解形式（22）和（25）带入方程组（26）中，可得：

同 |Δ|阶问题一样，方程组（27）的非齐次项包括与x、t相 关 的F11(x,t,y,T)和F21(x,t,y,T) ，以 及 与x、t无关的F21(y,T)和F22(y,T)。由于这两类强迫均可引起共振强迫，必须加以消除奇异条件的限制，通过消除奇异条件，得到关于振幅A(T)的方程：

其中，

3 高低指数环流的不连续性周期振荡

本节将进一步讨论高低指数环流的不连续性周期振荡，为此，需要给出两层模式的流场。分析式（22）、（25）和（29）可知， |Δ|1/2和|Δ|阶的解中含有斜压波振幅A(T) 。因此，需对 |Δ|3/2阶问题通过消除奇异条件得来的振幅方程（28）进行求解。

方程（28）为二阶非线性方程，将其改写为关于振幅A(T) 及其变化率的方程组，形式如下：

方程组（30）是自治的：有闭轨族Lh:H(A,S)=h，-k2(c+N|A(0)|2)＜h＜0 ；当h→0 时，Lh趋于同宿轨L；

其中H=S2-k2(c+N|A(0)|2)A2+k2NA4。

除上述闭轨族之外，分析平衡点的稳定性可知：方程（30）存在 (0,0) 和共3 个平衡点，其中 (0,0) 为鞍点，为中心。可见，在同宿轨L及两个中心之间，仍为闭轨族。

取纬向特征尺度L=3×106m ，铅直特征尺度H=103m ，纬 向 特 征 风 速U=10 m/s ，Rossby 参 数β=10-11m/s ，中纬度地转参数f0=4.87×10-4m-1， 纬向波数k=2 ，经向波数mπ=2 ，临界切变风速Uc=8 m/s，上层风速U1=12 m/s ，下层风速U3=9 m/s，斜压波速c=2 m/s 。由无量纲变换（4）可知：内旋Froude 数F=59.7 ，|Δ|=0.1，c0i≈4.215×10-4，N≈0.01087 ，γ=0.37。在这组参数下，中心点在原点附近。

因此，在一般的初始条件下，方程是在同宿轨L外的闭轨上运动。取初值A(0)=0和S(0)=1（从相图可以看出，初值并不影响其周期性），则得到A(T)-S(T)相图（图2）。

图2 具有跳跃性质的同宿轨道（ A(T)-S(T)）

由于c0i≪1和N≪1，则方程（30b）可近似为：

如图2 所示，在闭轨上半部，S≈1；在闭轨下半部，S≈-1。此时，在上半部和下半部之间，存在一个明显跳跃。分析时序变化（图3，已通过变换T=|Δ|1/2t进行了转换）可知：一方面，S(t)呈不连续性振荡；另一方面，S(t)在较长时间内呈现常数。波幅变化率S(t) 的整个图像类似于方形波，而波幅A(t)呈明显的跳跃特征。

图3 时序变化（a.S (t) ，b.A(t)）

将首次积分分解为如下形式：

这意味着，在大气运动的非线性作用下，无外源强迫的斜压运动是保守方程，总能量是守恒。

上文通过动力方程的方式，分析了波幅A(t)和波幅变化率S(t)的变化情况，二者的跳跃特征为分析西风环流的不连续振荡提供了基础。因此，结合式（18）、（20）、（22）、（25）和（29），可得到近似到 |Δ|阶 的 ψn解：

式中： -Uny(n=1,3)分别为两层模式的上层（400 hPa）和下层（800 hPa）的平均纬向流场， |Δ|1/2阶项为二者的线性波动， |Δ|阶项为二者的非线性波动，非线性波动保留了无量纲两层斜压涡度方程组（6）的非线性特征。

考虑到大气的高低指数环流主要出现在对流层的中上层，为此，下文主要针对上层（400 hPa）的流场ψ1来分析西风环流的不连续性周期振荡。一方面，由上文可知， γ=0.37 ，其与 |Δ|1/2接近，式（34 a）的第三项与第二项同量级。因此，在考虑ψ1的运动变化时，必须要考虑波幅变化率的作用。而根据图3可知，波幅变化率具有不连续性，并且在较长时间内处于定常状态（如第11 天到第17 天），这与西风环流的不连续特征具有一致性。另一方面，斜压波振幅A(t)及其变化率均为周期变化。可见，400hPa流场ψ1具有不连续性周期振荡特征。在上述取值条件下，可得出400 hPa 西风环流的空间结构变化（图4）。

图4 一个周期内400 hPa 西风环流 ψ1的空间结构变化（a.第1 天，b.第8 天，c.第9 天，d.第11 天，e.第14 天，f.第17 天，g.第19 天，h.第27 天，单位：3000 km）

从图3 和图4可以看出：从第1 天到第8天，斜压波振幅变化率为正，方程组（30）无奇点，西风环流为平直的纬向环流（图4a、b）；到第9天，振幅变化率由正转向负，方程组（30）出现了一对位置接近的对称的弱的双中心结构，该结构使得平直的纬向环流在南北向开始向中心弯曲（图4c）；随着振幅变化率快速变化，到第11天，位置接近的对称中心结构也急剧扩展为对称的偶极子结构，纬向环流转换为具有偶极型阻塞形势的经向环流（图3d）；振幅变化率在第11 天到第17天处于波谷（近似为常数），因此偶极型阻塞形势在这段时间内得以维持（图4e、f）；随后，振幅变化率快速变化，到第19 天，偶极子退化为弱的双中心结构（图4g）；到第20 天，振幅变化率由负转向正，方程组（30）无奇点，西风环流又恢复为平直的纬向环流（图4h），直到第28 天为一个周期。

分析线性稳定性可知，当F越大时，垂直切变临界值Uc也越大。这意味着，当垂直切变足够大时，斜压大气将会出现高低指数环流的不连续性振荡。进一步分析发现，高低指数环流不连续振荡过程中有三个关键点：（1）斜压波振幅A(t)由正转向负或由负转向正的过程中，发生了分歧，是造成纬向环流和经向环流的转换在比较短时间内完成的原因；（2）400 hPa流场 ψ1的非线性项，是产生偶极型阻塞形势的关键，而振幅变化率的方波特征，是能够较长时间维持具有偶极型阻塞形势的经向环流的原因；（3）斜压波振幅方程组（30）作为周期系统，通过斜压波振幅A(t)及振幅变化率调节非线性项的大小，控制偶极型阻塞形势的发展和消亡，是维持整个西风环流在纬向环流和经向环流间无限循环的原因。

4 结论与讨论

西风环流中长期变化是结构复杂的低频振荡，包括瞬变的Rossby 波、准定常阻塞形势的维持以及指数循环等多种振荡。探讨这些低频振荡是动力学研究中长期天气预报和气候变化的物理基础，而关于指数循环，由于其过程涉及到不连续性、分歧、周期振荡等非线性的复杂现象，一直没有得到彻底解决。为此，本文结合弱非线性理论和分歧理论，分析了高低指数环流不连续性振荡的物理机制，发现当垂直切变足够大时，西风环流出现不连续性周期振荡的原因主要有以下三个方面：（1）斜压波振幅的分歧，是造成纬向环流和经向环流的转换在比较短时间内完成的原因；（2）对流层中上层流场的非线性特征，是产生偶极型阻塞形势的关键，而斜压波振幅变化率的方波特征，是能够较长时间维持具有偶极型阻塞形势的经向环流的原因；（3）斜压波振幅及振幅变化率通过周期性的调节非线性项大小，控制偶极型阻塞形势的发展和消亡，是维持整个西风环流在纬向环流和经向环流间无限周期循环的原因。

需要指出的是，本研究仅考虑了无外源的斜压模式，这导致斜压方程是周期性的，而非准周期性。因此，下一步将考虑外源强迫对方程的影响，进而更全面地揭示高低指数环流不连续性准周期振荡的物理机制。