兼顾空间公平和效率的社区公园布局优化模型构建与验证∗

诸逸凡 刘志强 余 慧 洪亘伟

苏州科技大学建筑与城市规划学院 江苏苏州 215011

社区公园是社区生活圈内重要的绿色开放空间, 使用频率高、 就近为居民提供日常游憩服务,是其区别于其他类型公园的核心价值所在[1]。 近年来, 我国国土空间规划逐步进入以社区生活圈为单元的精准化调控阶段, 积极推进基本公共服务均等化[2－3], 社区公园布局的空间公平、 空间效率愈发重要, 是社区公园布局的重要价值导向[4－6]。 空间公平是保证居民平等享有社区公园服务的根本, 空间效率则强调社区公园资源的高效利用。 在城市开发建设转向存量提质改造和增量结构调整并重的背景下, 以兼顾空间公平和空间效率(下文简称兼顾空间公平和效率) 作为社区公园空间布局的基本原则, 构建具有可操作性的社区公园布局优化模型, 对优化社区公园供需匹配状况、 实现其公平分配与高效配置具有重要意义。

近年来, 基于空间公平和效率的公园绿地布局优化研究主要包括: 1) 研究视角上, 一方面基于空间公平视角, 关注“人的需求”, 根据供需关系研究公园绿地空间布局优化[5－6]； 另一方面基于空间效率视角, 通过绩效衡量测评为空间布局优化提供建议[7]。 仅有陆砚池和方世明[8]等少量学者基于均衡和效率的双重视角研究公园绿地布局。 2) 研究对象上, 以公园绿地为主要研究对象[4－9]。 部分学者将包含微绿地在内的一类社区公共绿地作为研究对象[10], 如杨琛等[11]、杜伊等[12]针对社区公园、 社区公共绿地的布局优化展开研究。 3) 研究方法上, 多基于可达性等评价指标, 结合绩效评价、 基尼系数等方法, 提出公园绿地空间布局优化建议[9－11]。 也有学者逐步采用布局优化模型解决公园绿地布局决策问题[13], 如李俊英等[14]运用人口重心模型定量表征与模拟沈阳市绿地优化格局。 布局优化模型已在公共服务设施布局优化研究中被广泛使用, 现有常见模型主要有经典区位分配模型和公平最大化模型[15－16], 前者包含P 中值、 最大覆盖等基础模型, 主要优化设施区位； 后者则关注设施规模的优化。 二者在模型构建和求解方面均有深入而广泛的拓展[17－18]。 但仍有以下内容有待拓展: 1)基于兼顾空间公平和效率视角的社区公园布局优化研究有待进一步开展； 2) 契合社区公园供需特点, 精准化实现其空间布局优化的模型有待构建。

合理的社区公园空间布局有助于落实公园体系分级分类配置[19], 亟需具备科学性、 可操作性的社区公园布局优化模型以提供直观布局方案。 基于此, 本文以先选址、 后分配规模的两步优化模型形式, 融合P 中值、 公平最大化模型的目标函数, 并添加约束条件, 构建兼顾空间公平和效率的社区公园布局优化模型, 再以苏州市中心城区为实证区域, 验证模型有效性, 以期为规划实践提供社区公园空间布局优化模型, 推进实现社区公园服务均等化, 为构建高品质社区生活圈提供借鉴。

1 模型构建

1.1 基础模型分析

田玲玲等[20]发现, P 中值模型在公共设施服务范围较小时效果优于其他经典区位分配模型。 同时, 公平最大化模型以公平为导向, 在设施布局规模优化层面有显著优势[15]。 因此, 本文以P 中值模型作为优化空间效率的基础模型, 以公平最大化模型作为优化空间公平的基础模型, 对二者进行适用性分析并结合社区公园布局需要确定改进方向。

1.1.1 以空间效率为价值导向的P 中值模型分析

P 中值模型追求需求者与最近设施之间总出行成本最小化, 以获得空间效率导向下的最优设施区位。 “邻近分配” 原则, 即需求者仅与最近的设施建立联系, 而居民前往社区公园的意愿受出行成本影响, 适用于“邻近分配” 原则。 因此, P 中值模型的目标函数适用于优化社区公园布局的空间效率, 但仍有两部分内容需要针对性改进: 1) P 中值模型仅能够优化区位, 无法实现规模优化； 2) P 中值模型以空间效率为导向的优化方式, 倾向于选址远离人口较少的区域[15], 与社区公园布局的空间公平原则不符。

1.1.2 以空间公平为价值导向的公平最大化模型分析

公平最大化模型由王法辉[16]在2013 年首次提出, 通过追求各需求点到公共设施的可达性差异最小化实现公平最大化。 公平最大化模型利用可达性指标判断区域供需差异并优化设施规模,但将其运用于社区公园规模优化仍需关注两点:1) 社区公园遵循先选址、 后分配规模的优化流程[20－21], 在未确定区位时无法使用公平最大化模型； 2) 社区公园规模受到用地范围及周边设施等多方限制, 为其分配规模需在一定限度下进行。

1.2 模型构建

研究从模型形式、 目标函数、 约束条件3 个方面构建兼顾空间公平和效率的社区公园布局优化 模 型 ( Equity-Efficiency Community Park Allocation Model, 2ECPA) (图1)。

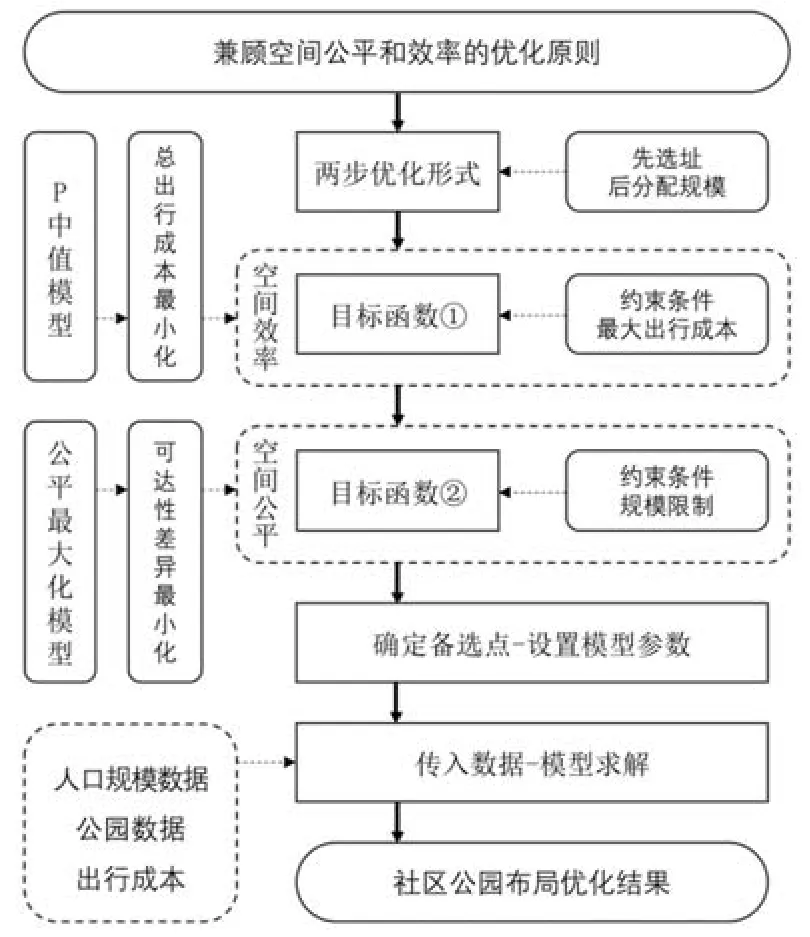
图1 2ECPA 模型构建、 优化路线

1.2.1 模型形式

改变社区公园区位、 规模中的任一要素, 都需要考虑其对空间公平、 空间效率同步产生的影响。 因此, 模型采用先选址、 后分配规模的两步优化形式, 分步求解区位与规模[20－21], 并兼顾空间公平和效率。 1) 优化社区公园区位, 在生成的T个社区公园备选点中, 选择预设数量p个社区公园, 形成最优区位。 2) 优化社区公园规模,为选取的p个社区公园分配规模, 以就近满足居民的游憩需要, 形成最优规模。

1.2.2 目标函数

将P 中值模型与公平最大化模型的目标函数与两步优化的模型形式融合。 1) 嵌入总出行成本最小化的目标函数以确定2ECPA 模型条件下的社区公园最优区位, 提高社区公园供给与居民需求在空间上的匹配精准度, 优化空间效率。 2)嵌入可达性差异最小化的目标函数以确定社区公园个体规模, 提高不同区域间社区公园供给与居民需求匹配的均等化程度, 优化空间公平。

1.2.3 约束条件

为保证2ECPA 模型兼顾空间公平和效率, 且适用于社区公园空间布局优化, 在目标函数增设约束条件。 1) 在总出行成本最小化的目标函数下,添加最大出行成本作为约束条件, 避免社区公园选址远离人口较少的区域, 实现选址过程中优化空间效率且兼顾空间公平。 2) 在可达性差异最小化的目标函数下, 添加社区总规模及个体规模限制作为约束条件, 强调社区公园资源有限下的可达性差异最小化, 以及使建设的社区公园符合政策标准。

1.2.4 模型构建步骤

步骤1: 优化空间效率且兼顾空间公平, 计算公式为:

式(1) ~ (5) 中:i为居民区；m为居民区合集；j表示社区公园备选点；n为社区公园备选点合集；Di为居民区i的需求量；ωij为居民区i与社区公园备选点j之间的出行成本；p为预设的社区公园总数量；Yij表示社区公园备选点j是否为居民区i提供服务, 取1 为提供服务, 取0 为不提供服务；Xj表示社区公园备选点j是否建设社区公园,取1 为会建设, 取0 为不会建设。 其中, 式(1)为总出行成本最小化的目标函数； 式(2) 保证优化后社区公园总数量为预设的总数量p； 式(3)保证居民区必须且只与一个社区公园建立联系； 式(4) 保证每一个社区公园都有服务对象； 式(5)保证居民在最大出行成本ω0范围内均可获得社区公园服务, 依据“15 分钟社区生活圈” 理念及居民出行方式, 确定ω0为15 min 骑行时间。

步骤2: 优化空间公平, 计算公式为:

式(6) ~ (9) 中,a为人均社区公园可达性；Di、Dk为居民区i、k的需求量；D为所有居民区的总需求量；Sj为社区公园j的规模；G为衰减函数；S为社区公园的预设总规模。 其中, 式(6)为可达性差异最小化的目标函数； 式(8) 保证优化后社区公园总规模为S； 式(9) 约束新增社区公园的规模应为10 000~100 000 m2。

2 模型验证

2.1 实证区域概况及数据来源

苏州市中心城区包括姑苏区全域与吴中区、相城区、 高新区和工业园区部分街道, 面积约为437 km2。 中心城区作为苏州市发展的核心区域,人口高度集聚, 公园数量多, 因此, 以该区域作为实证区域, 能准确研判模型优化效果。 实证所需数据及来源如表1 所示。

表1 数据用途及来源

2.1.1 居住区及人口规模

本文借用Python 语言从链家网获取2022 年5月苏州中心城区范围内居住区数据。 根据«苏州统计年鉴2021»中户均规模计算,苏州市中心城区约为214 万人,主要集中在姑苏区及其周边区域,工业园区人口相对分散(图2)。

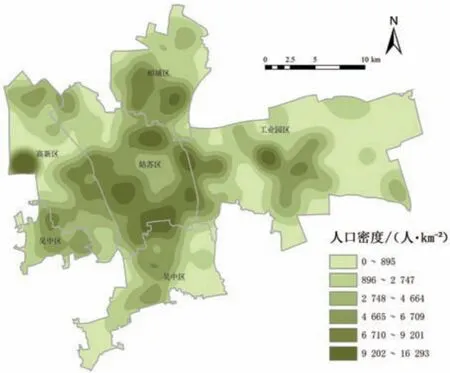
图2 苏州市中心城区人口密度

2.1.2 社区公园区位及规模

为消除靠近边界的居民难以在边界范围内有效获取资源时,倾向于向边界外设施就近寻求资源的边界效应影响,在中心城区周边设定15 min 骑行距离的缓冲区,从高德地图开放平台采集得到苏州市中心城区、缓冲区内公园绿地AOI 数据。

邱冰等[22]、何琪潇等[23]均提及服务于周边社区的综合公园具有社区公园的功能,所以下文将综合公园视作提供社区公园服务。 结合«城市绿地分类标准»(CJJ/T85－2017)和苏州市园林和绿化管理局(http:/ /ylj.suzhou.gov.cn/szsylj/index.shtml) 公开的公园绿地规划信息, 筛选得到69 个能够提供社区公园服务的公园, 总规模为4 204 433 m2(图3)。

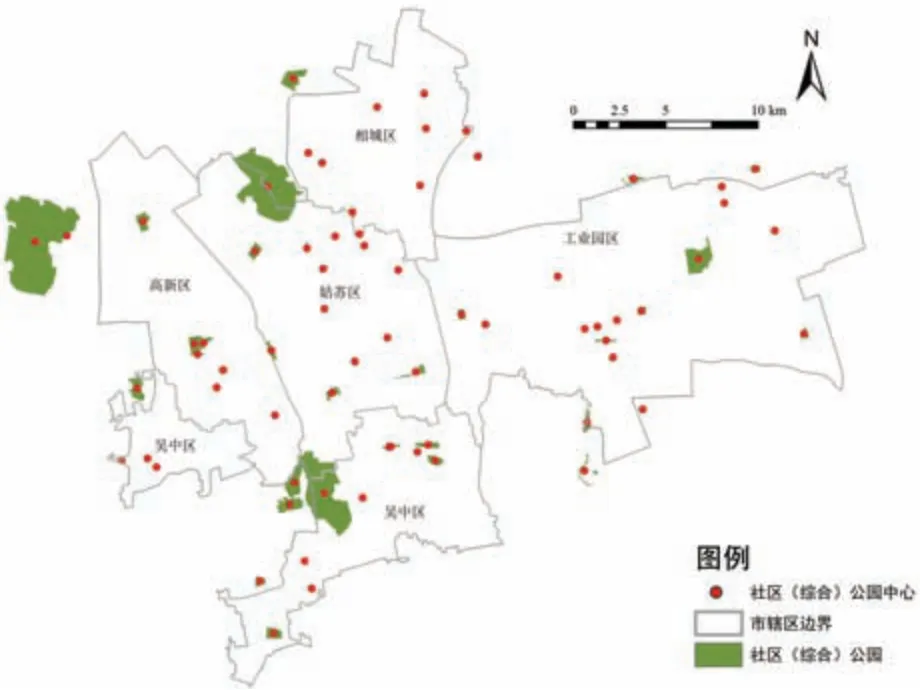
图3 苏州市中心城区社区公园布局现状

2.1.3 出行成本

本文利用高德地图路径规划API, 获取居民抵达公园的时间和距离成本。 2ECPA 模型求解时, 选取时间成本作为出行成本, 在实证结果比较时, 为便于计算, 统一换算为由路径规划API获取的对应距离成本进行比较。

2.2 模型有效性验证

当社区公园总规模、 数量增加时, 即使新增社区公园不符合理想区位与规模, 空间公平和效率也存在提高的可能性。 因此, 为验证模型有效性, 确保社区公园总规模、 数量不变, 基于Matlab2021b 软件, 通过2ECPA 模型优化社区公园区位、 个体规模。

2.2.1 有效性检验参数设定

设定社区公园总数量p为69, 社区公园总规模S为4 204 433 m2。 根据实证区域大小, 去除苏州市中心城区现有大型水域、 教育科研用地、 行政办公用地、 医疗用地、 部分居住用地及特殊性质用地, 并结合土地利用规划以及相关标准及规范, 考虑现存设施的动迁难易程度, 将剩下区域划分为单个面积为10 hm2的4705 个网格, 形成备选点网格集(图4)。

图4 社区公园备选点网格集

2.2.2 有效性验证结果

模型优化后的社区公园区位及规模与现状相比存在明显差异(图5)。 选用表2 内4 项指标对优化前后社区公园布局进行评价比较, 结果表明:优化后15 min 出行时间内能够到达社区公园的居民增加了5.87%； 居民到达邻近社区公园的最大出行成本、 平均出行成本分别降低56.95%和12.12%； 居民的社区公园可达性基尼系数下降31.48%, 由差距悬殊转变为差距相对合理。 在社区公园数量、 总规模保持不变的条件下, 社区公园布局空间公平、 空间效率均提高, 证明模型有效。

表2 模型有效性验证结果

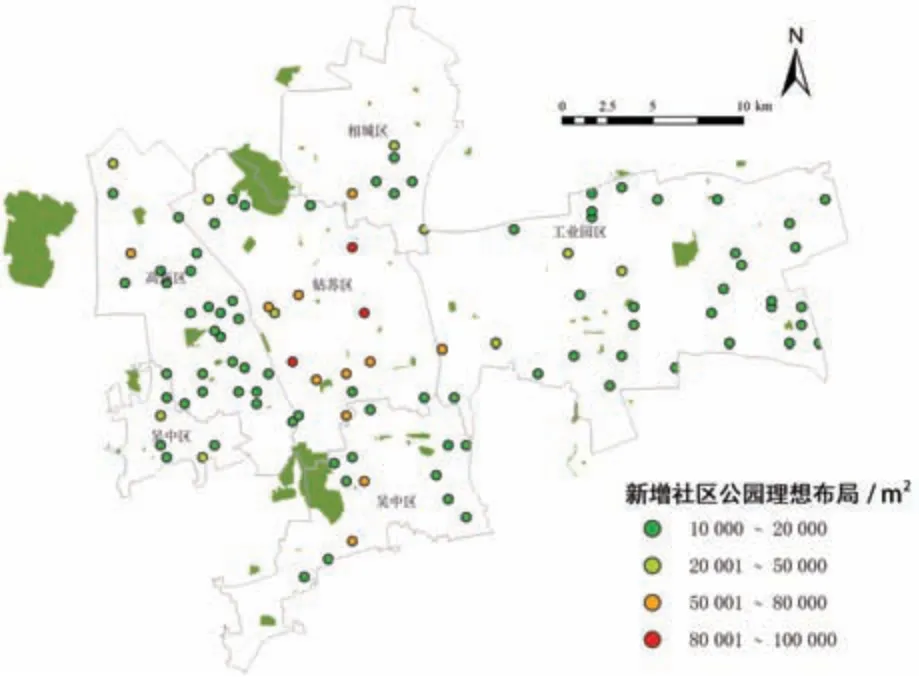
图5 有效性验证布局结果

2.3 苏州市中心城区社区公园空间布局优化

证明模型有效性后, 以«园林绿化工程项目规范» (GB 55014－2021) 规定的人均社区公园面积3.0 m2/人为优化条件, 在不改变现有公园布局的基础上, 利用Matlab2021b 下的yalmip 工具箱实现2ECPA 模型求解, 探究苏州市中心城区内的新增社区公园空间布局理想优化方案, 以兼顾空间公平和效率的优化。

2.3.1 空间布局优化参数设定

中心城区社区公园总规模尚需增加2 232 056 m2,原有社区公园规模4 204 433 m2, 即设定优化后社区公园总规模为6 436 489 m2。

本研究以社区公园区位选址实现当前p取值下社区公园全覆盖, 且新增社区公园数量最少为理想目标, 运用2ECPA 模型求解得到p在92~292 区间取不同值时社区公园最优区位的总出行成本及该p取值下所有区位中的总出行成本最小值并计算差值(表3)。 当p取值到达174 后, 差值为0, 即2ECPA 模型所得到的社区公园最优区位在覆盖所有居民的同时, 使得该p取值下不存在另一类区位选址的总出行成本比2ECPA 模型得到的最优区位下总出行成本更小。 因此, 设定社区公园总数量p的取值为174。

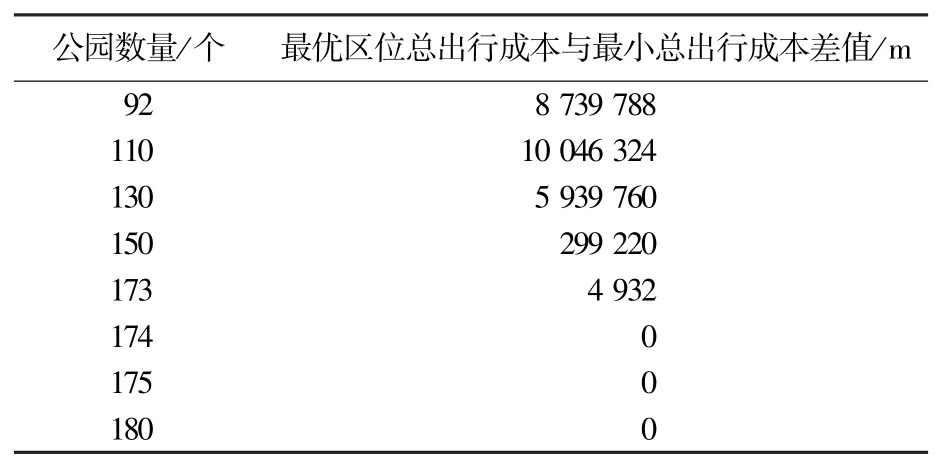
表3 2ECPA 最优区位的总出行成本差值结果

在图3 备选点网格集的基础上, 去除现有公园所在区域及其15 min 骑行范围内的备选点, 形成新增备选点网格集。

2.3.2 空间布局优化

求解得到社区公园区位及规模(图6), 与现状布局相比较, 各市辖区均有新增社区公园(表4)。 理想布局中的社区公园多数规模较小、 分布较广, 与«苏州市“公园城市” 建设指导意见»中提及的新增200 余个小型公园, 完善社区和口袋公园网络的建设指导意见相契合, 一定程度上反映了布局科学性。

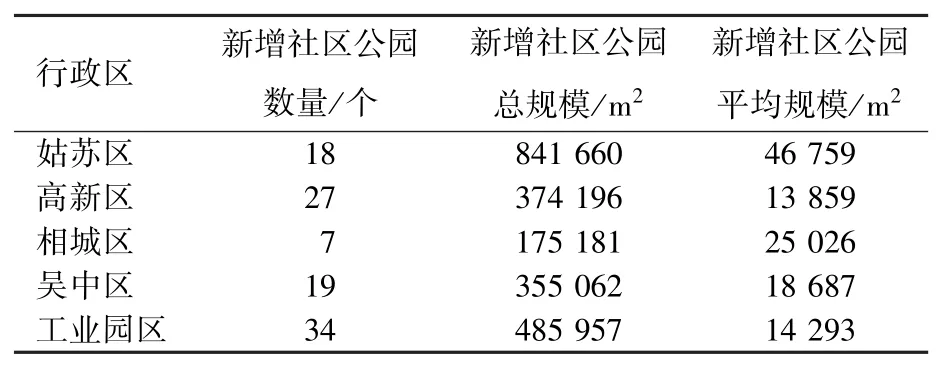
表4 苏州市中心城区社区公园空间布局优化结果

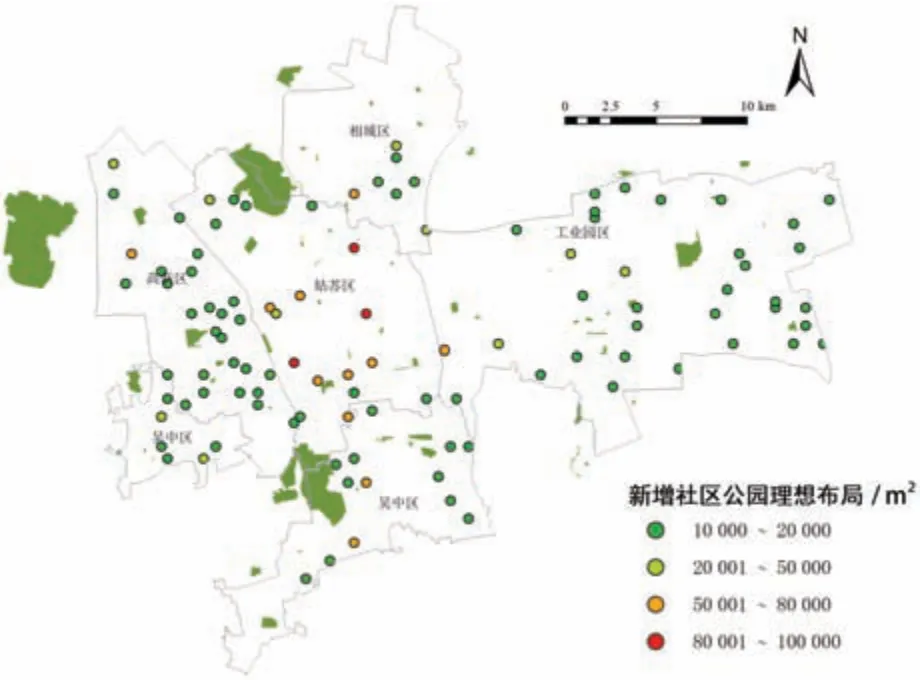
图6 苏州市中心城区社区公园空间布局优化结果

进一步比较优化前后社区公园空间布局, 结果(表5) 发现, 中心城区居民均可在15 min 的时间阈值内到达邻近社区公园, 最大、 平均出行成本分别下降67.99%和41.58%, 社区公园可达性基尼系数下降24.07%, 由差距悬殊转为差距较大, 并趋近于相对合理。 优化后社区公园覆盖人口比率提高, 居民能够更便捷获取社区公园服务,可达性基尼系数显著下降, 实证区域内社区公园布局空间公平和空间效率均显著提升。

表5 优化前后社区公园空间布局比较

3 模型应用前景

本文构建的2ECPA 模型具备可操作性、 可借鉴性及可拓展性, 并基于居住区尺度数据进行了苏州市中心城区的实证研究, 检验模型优化效果。模型运用时, 数据的精度、 来源会对优化结果产生影响, 数据精度越高、 来源越可靠, 模型优化结果越准确。 同时, 在实践中可从3 个方面对模型进行拓展运用:

1) 模型具备根据需求确定参数且理论上适用于不同尺度区域的可操作性。 使用者能够根据需求, 确定社区公园的建设数量、 总规模并直接运用2ECPA 模型进行布局优化。 同时在理论层面上, 模型运用并不局限于城市尺度下的区域, 在不同尺度下对模型进行验证后, 使用者可根据需求进行调整, 在市辖区或街道等更小尺度下的区域内均可使用。

2) 模型具备修改约束条件、 目标函数, 构建适用不同公园绿地布局优化模型的可借鉴性。 一是使用者可依据城市公园绿地的建设状况, 修改约束条件, 构建适用于当前城市布局要求下的社区公园布局优化模型。 二是沿着2ECPA 模型的构建思路, 还能够构建其他公园绿地的布局优化模型。 如修改最大出行成本为30 min 驾车时间、 个体规模限制为大于10 hm2, 以可达性最大化为规模分配的目标函数, 可初步构建适用于综合公园空间布局优化的模型。

3) 模型具备改进为多目标优化模型, 结合引进智能算法, 实现区位、 规模同步求解的可拓展性。 公共服务设施领域已有通过智能算法与权重赋予的方式[24], 解决多目标公共设施布局决策问题的研究。 社区公园空间布局优化实质是一类复杂多目标决策问题, 除出行成本与可达性差异外,还存在其他目标用以表征空间公平与空间效率,可增加更多目标函数, 并引入智能算法, 求解社区公园布局的多目标问题。

4 结语

本文指出社区公园在空间布局过程中, 空间公平和空间效率相互影响, 且社区公园数量、 区位或规模的变化均可能造成二者改变, 须遵循兼顾空间公平和效率的优化原则来构建2ECPA 模型。 以苏州中心城区为实证区域, 验证模型有效性后进行布局优化, 优化结果显示社区公园布局的空间公平和空间效率显著提高, 体现出模型具有科学性与可操作性。 2ECPA 模型能够有效应用于社区公园空间布局优化, 提供直观的社区公园布局方案。