基于WHI及ICP的点云配准算法
2024-01-15王正家苏超全
王正家,苏超全,聂 磊
(1.湖北工业大学机械工程学院,湖北 武汉 430068;2.湖北工业大学现代制造质量工程湖北省重点实验室,湖北 武汉 430068)
1 引 言
随着3D成像技术的兴起,激光扫描仪在机器人、智能制造、文物保护等领域得到了广泛的应用[1]。然而,在实际扫描过程中,由于测量环境和仪器设备等因素的影响,通常需要对物体多视角扫描,并通过配准把不同视角的点云变换到同一坐标系下[2]。点云配准通常分为粗配准和精细配准[3]。粗配准算法主要有人工设计的特征配准、基于学习的特征配准[4]、随机样本一致性(Random Sample Consensus,RANSAC)、概率分布配准和基于投影的配准[5]。精确配准主要包括Besl[6]等提出的迭代最近点(iterative closest point,ICP)算法,ICP算法时间复杂度高,需要良好的初始位姿,不然容易陷入局部最优。Chetverikov、Dong等人对ICP的改进提高了算法的效率和准确性[7-8],对于数据量大的情况下迭代耗时。Biber[9]提出了基于概率密度分布的NDT算法,算法精度高、计算速度快但对初始位姿有一定的要求。Rusu[10-11]提出了持久特征直方图配准(Persistent Feature Histograms)算法,计算复杂度高,速度慢,接着提出优化后的快速点特征直方图(Fast Point Feature Histograms,FPFH)描述符,基于样本共识的方法(Sample Consensus Initial Align,SAC-IA)进行特征配准,提高了配准速度,克服了点云位置的局限性,配准精度不高。考虑到粗配准和精确配准优缺点,两步配准算法成为了主流。荆路等人[12]提出一种基于FPFH的SAC-IA和NDT(Normal Distributions Transform)融合的点云配准方法,点云采样的大小对配准速度有很大的影响以及NDT的配准精度相比ICP稍微降低。赵明富、宋涛等人[13]提出了基于FPFH融合采样一致性和迭代最近点算法的点云配准方法,解决了ICP算法陷入局部最优的问题,在计算FPFH特征时耗时有待于进一步改进。刘今越等人[14]提出一种基于曲率精简点云,融合NDT与ICP的点云配准算法提高了点云配准的速度,模型数据不具普适性。Sun T等人[15]提出结构紧凑的加权高度图像描述符(Weighted Height Image,WHI),并用于点云粗配准,配准精度、效率高。
针对点云两步配准效率低、配准精度差的问题,提出ISS算法(Intrinsic Shape Signatures,ISS)精简点云,通过WHI描述符完成粗配准,利用安德森算法改进ICP完成点云的精确配准。实验表明所提算法的速度、精度都有一定程度的提高,在噪声环境下配准效果良好。
2 加权高度图像描述符
加权高度图像描述符(Weighted Height Image,WHI)是一种三维信息二维离散化的表达,主要包括简化LRF(local coordinate reference system,LRF)和基于良态空间优化的加权编码两个部分。
2.1 局部坐标参考系
一个独特的、可重复的、鲁棒的局部坐标参考系对于特征描述是非常重要的[16]。LRF估计一般通过局部点云的协方差矩阵特征值分解得到:
(1)
式中,pf为特征点;r是搜索半径;pi为支持域内的点;μ邻域控制因子,di=‖pi-pf‖2。
协方差矩阵中,对离特征点较远的邻域点进行了较小权值的加权,这可以在遮挡存在的情况下增加LRF的可再现性。由于协方差矩阵C(pf)是实对称矩阵,对其进行特征值分解可以得到:
C(pf)=QΛQT
(2)
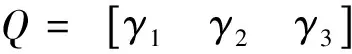
(3)

(4)
(5)
然后根据坐标分量和定义坐标轴的方向,如下:
(6)
(7)
signy=signx×signz
(8)
定义一个符号向量S=[signxsignysignz]T,则支撑区域内各点的最终坐标可表示为:
(9)
其中,RLRF=SRam,是符号重定向后的局部坐标系。
2.2 WHI特征描述符生成
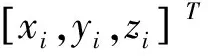
(10)
提出一种权函数对编码函数进行加权,以使得特征空间更加逼近于良态空间,权函数定义为:
0<η≤1
(11)
其中,r是搜索半径,di(x,y,z)是点pf与点pi的距离,η是权函数值域范围的控制因子,它使得W(x,y,z)的值域为[η,1]。则优化后的编码函数见下式:
F(x,y,z)=W(x,y,z)Fz(x,y)=
(12)
Fz(x,y)=z,为了生成描述符,编码函数应该重新编码或直接离散成描述符。在pf建立LRF,点pf的切平面是由基点pf和它的法向量n唯一决定的。另外两个正交分量nz,ny位于平面内。落入支持区域的点沿法向量投影到平面上。图像的像素值由所有加权高度的平均值决定,而不是由最小距离决定。WHI计算公式见下式:
(13)
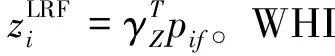
(14)
其中,D是局部高度图像对应的正方形区域(D:-R≤x≤R,-R≤y≤R)。则x方向(用随机变量X表示)对应的边缘概率密度函数为下式:
(15)
同理:
(16)
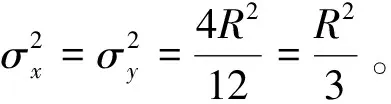

(17)
采用的卷积核尺寸为5×5。利用该滤波器对局部高度图像进行滤波并保持分辨率不变,最后将滤波后m×m的局部高度图像按照一定顺序展开成一维向量,即可得到该特征点的WHI描述子。
3 特征点提取及点云配准
3.1 ISS算法
由于点云数量较大,一般提取点云中几何特征明显的点来代表整体点云。ISS算法具有丰富的几何信息,可以完成高质量的点云配准。ISS特征点算法检测原理如下:
Step1:利用kd_tree构建三维点云k邻域内的拓扑结构,从而利于三维点云的搜索;
Step2:假设三维点云中的查询点为Pi,邻域的点集N(pi)={pij,j∈{1,2,…,k}}pij表示邻域内的点,对于邻域内的中心点:
(18)
Step3:依据欧式距离计算点pij的权值,见下式:
(19)
Step4:构建协方差矩阵:
(20)
Step5:求协方差矩阵从大到小排列的特征值λi1λi2λi3,以及对应的特征向量ei1ei2ei3。
Step6:设置筛选特征点的阈值ε1和ε2,满足以下条件的点设置为关键点:
(21)
(22)
通过对三维点云的ISS特征点作为采样点进行点云的配准,精简点云数量,降低点云特征描述的复杂度,有利于提高点云配准的速度。
3.2 基于WHI的粗配准
(1)对源点云、目标点云提取ISS特征点计算点对的WHI特征;
(2)利用kdtree算法搜索相近特征的对应点对,作为对应点对;
(3)从对应的点集中随机选取四个对应点对,采用SVD算法计算源点云与目标点云之间的变换矩阵;
(4)对应点对的源点云进行变换,计算变换后的点云与原对应点对的目标点云的欧式距离,如果小于一定阈值作为内点记录,否则记为外点;
(5)重复(2)~(4)步直到迭代次数达到设定阈值,选择最多一个内点的记录,利用迭代矩阵对源点云进行变换。
3.3 基于ICP改进的精配准
3.3.1 安德森加速算法
(23)

(24)
研究表明,Anderson加速法是求残差函数的根的一种拟牛顿方法,对于线性收敛的不动点迭代,Anderson加速法可以提高收敛速度[18]。
3.3.2 安德森加速的ICP点云配准算法
传统ICP配准算法写成关于需要求解的关于R,t固定点迭代的形式:
(25)
(26)
ΠQ(·)表示在投影在点集Q的最近点。然而,我们不能直接将Anderson加速度应用于映射GICP。这是因为安德森加速度将计算R的新值作为旋转矩阵的仿射组合,这通常不是一个旋转矩阵本身。为了解决这个问题,使用另一组变量X来参数化一个刚性变换,这样X的任何值都对应一个有效的刚性变换,并且ICP迭代可以重写为式(27)的形式[19]:
(27)
然后我们可以通过在每次迭代中执行以下步骤对变量X应用安德森加速度:
(1)从x(k)计算旋转矩阵R(k)和平移向量t(k);
(2)ICP迭代更新:
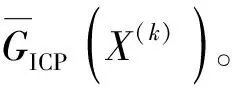
(4)计算加速值XAA。
Rd中的所有刚性变换都形成了特殊的欧几里得群SE(d),这是一个李群,并产生了一个李代数SE(d),它是一个向量空间。可以使用se(d)中对应的元素将刚性变换参数化。每个点的齐次坐标p=[pT,1]T,刚性变换T通过旋转矩阵平移向量表示:
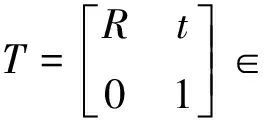
(28)
对于齐次坐标,所有这些矩阵形成特殊的欧几里得群SE(d)。它的李代数se(d)包含如下形式的矩阵:
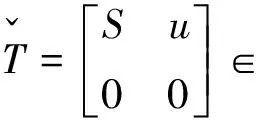
(29)
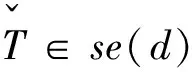
(30)

4 实验和分析
实验选取不同的点云模型进行研究,通过点云配准的精度、时间作为配准指标,所提算法和几种先进的算法进行比较证实所提算法的先进性。
4.1 实验数据和实验条件
为了验证本文算法的有效性,通过两组不同数据对文献[12]算法,文献[13]算法、文献[15]算法及所提的算法进行比较。实验数据选用斯坦福3D扫描库(http://graphics.stanford.edu)下载的Bunny模型和Dragon模型,Bunny模型选用bun000和bun045数据,Dragon模型选用dragonStsndRight_0和dragonStsndRight_24点云数据。实验电脑配置为Intel(R)Core(TM)i5-6200的CPU,内存12 GB,使用VS 2019配置PCL1.12.0点云库展开实验。
实验中待配准点云模型的初始位置如图1,灰色为待配准点云,黑色为目标点云。

图1 点云配准前的Bunny、Dragon模型
4.2 评价指标
(1)精确度指标

(31)
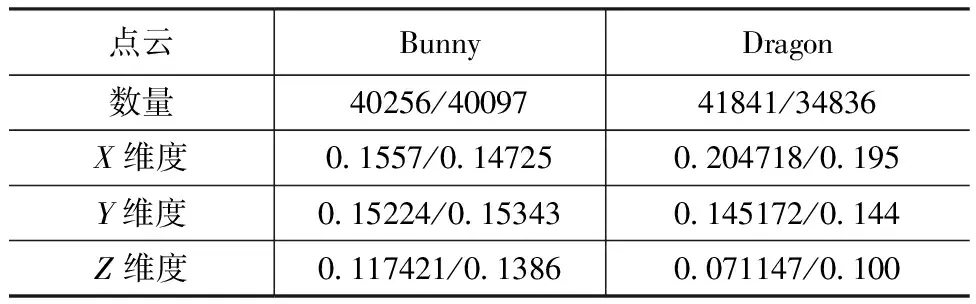
表1 原始点云的维度
表1中/的左右数值分别表示待配准点云、目标点云属性的具体值。X、Y、Z维度表示边界框的三个维度,边界框是包裹点云的体积最小的长方体。
(2)速率指标
点云配准的效率可以通过运行的时间进行评估,由于实验环境,算法原理不同,通过多次实验求取平均值作为点云配准算法的最终时间。
4.3 点云配准时间和精度
从配准时间与精度方面,将所提算法与几种常见的配准算法进行了对比,结果如表2所示。SAC-IA+NDT[12]首先计算FPFH特征,然后利用SAC-IA方法作为粗配准,NDT算法做为精配准。SAC-IA+ICP[13]以DNT方法进行粗配准,ICP方法进行精配准。WHI+ICP[15]通过体素下采样,通过点云的WHI特征构建对应点对进行粗配准,ICP算法完成精配准。
所提方法利用ISS算法提取特征点完成点云精简,然后利用WHI描述符进行粗配准,基于安德森加速ICP的方法进行精配准。不同点云模型下的配准精度和配准效率见表2。
从表2可以看出,所提算法在Bunny点云数据的配准时间为4 s左右,较SAC-IA+NDT、SAC-IA+ICP、WHI+ICP方法的22 s、26 s、6 s左右,在配准效率上分别提高了450 %、550 %、50 %。所提算法在Bunny点云配准的精度为0.0029943,较前三种算法的大致提升了10 %以上。在Dragon模型中,所提算法的配准时间为5 s左右,较前三种算法的23 s、28 s、10 s,分别提升了360 %、440 %、50 %左右。所提算法在Dragon模型配准的精度为0.00176953,较SAC-IA+ICP、cNDT+ICP三种算法分别提升了5 ‰左右,相对于SAC-IA+NDT算法提升了39 %左右。所提算法相较于其他三类算法在点云数据配准过程中具有明显优势。
4.4 点云配准算法关键问题分析
(1)ISS算法分析
体素下采样算法在精简点云方面具有广泛的应用,下采样的点云为原始点云的近似点云。ISS算法提取的特征点为配准点云集中的点,速度慢于体素下采样算法,基于几何特征的优势相比于体素下采样算法更具显著性。实验选用斯坦福的Armadillo模型进行实验,初始位姿如图2所示。
图2 点云配准前的Armadillo模型
在实际中由于传感器、扫描环境的影响,点云获取过程中不可避免的产生噪声,选取Armadillo模型验证算法在噪声环境下的影响。ISS算法提取后的配准点集如图3所示。

图3 Armadillo模型的ISS特征点集
提取后的配准点集通过WHI进行粗配准如图4所示。

图4 Armadillo模型粗配准
基于ISS与WHI特征描述子粗配准后,模型大致重合,能够为点云精确配准提供良好的初始点集。基于体素下采样和WHI的粗配准算法未能配准成功。基于体素下采样的特征点包含噪声点的信息,对点云粗配准有很大的影响,ISS算法过滤了噪声点。因此所提算法在噪声环境下具有一定的鲁棒性。
(2)安德森加速的ICP算法分析


图5 Bunny模型三点配准
为确定良好的m值,实验采取单一变量法,改变m值,记录加速的ICP算法收敛时点云配准的误差和配准时间,如图6,图7所示。m的取值对点云配准的精确度影响比较小,m取值为5时获得良好的配准速度,与文献[20]中安德森算法在几何优化中的理论相符。
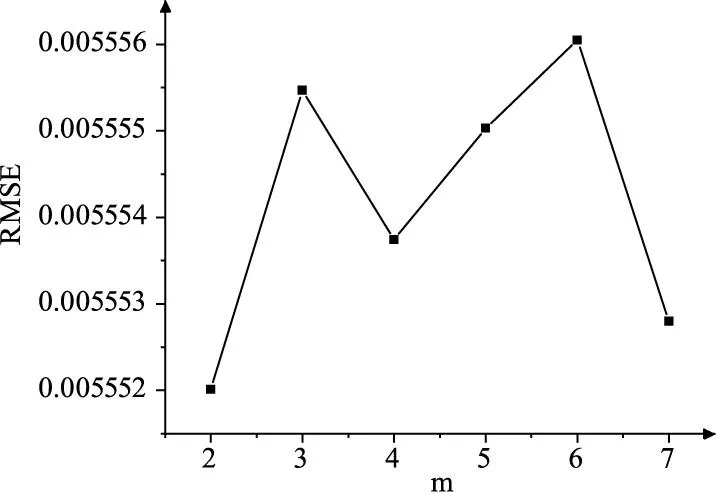
图6 先前迭代次数对点云配准误差影响
为验证改进的精配准算法的可行性,采用基于WHI的配准算法对Bunny模型进行粗配准,然后利用基于安德森算法的ICP算法进行精配准。所提算法与传统的ICP算法配准的RMSE随着迭代次数的变化如图8所示。
从图8中看出,基于安德森的ICP配准算法迭代速度快,精度略有提高。实验中基于安德森的ICP算法运行时间约为0.976s,ICP算法约为3.225s,配准效率提高了2.3倍左右。在同等配准精度下,所提算法迭代速度快于ICP算法,可在满足配准精度要求下调整迭代次数进一步提高点云配准速度。
4.5 点云配准性能测试
点云数据获取过程中经常会受到一些外界的干扰,点云配准算法应该具有一定的抗噪能力,在实验中选取Bunny模型以及Dragon模型分别进行实验,首先对两种模型加入均值为0以及标准差以0.001为间隔的高斯噪声得到含有噪声的数据。
从图9图10中看出在点云配准成功情况下,随着噪声的增加几种算法的配准精度都有所提高,这和精度的评价标准有关,RMSE的评价指标会过滤掉一些错误的配准点对,因此计算出的点云的配准精度有所提高,SAC-IA+ICP算法在Bunny模型配准成功,在Dragon实验中配准失败,其他几种算法均能配准成功,配准精度相差无几,所提算法相对精度略高一些。
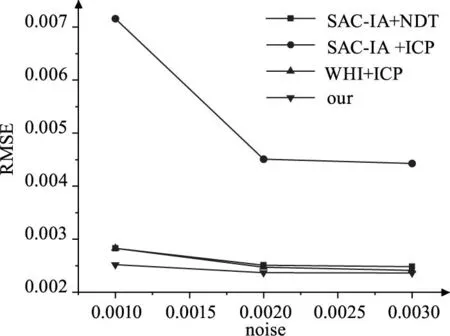
图9 Bunny模型配准误差
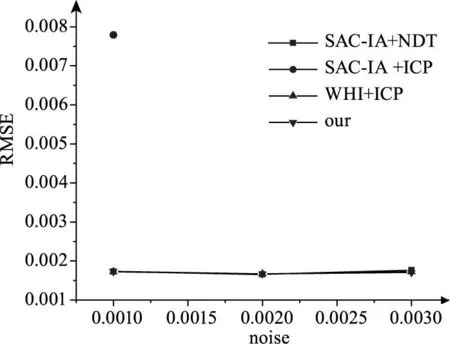
图10 Dragon模型配准误差
4.6 真实环境下点云配准性能测试
为了验证该算法在实际工程应用中的有效性,分别选取室内、室外真实点云数据进行实验,分别来自PCL官网[21]和文献[22]提供的数据集,如图11、图12所示。

图11 点云配准前的Room模型

图12 点云配准前的Arch模型
图11的点云模型灰色为room_scan1,黑色为room_scan2。图12为室外真实场景,灰色点云为s01,黑色为s02。室内室外场景的点云数据都存在噪声与离群点,最能真实反映算法的可行性,所提算法可视化结果见图13、图14,算法配准时间见表3。
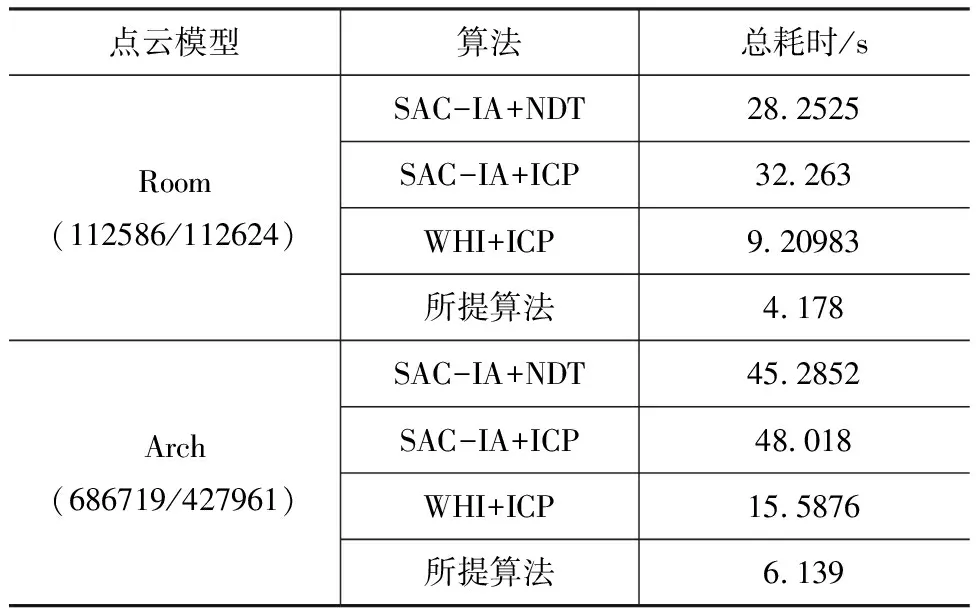
表3 真实场景配准时间

图13 Room模型配准可视化

图14 Arch模型配准可视化
在噪声和离群点存在的情况下利用RMSE进行误差计算不合适,因为会包含一些无关点对的计算,从表中看出在含有噪声、离群点的情况下所提算法配准效率更高,在含有噪声的不同场景中配准速度提高了2倍以上。
5 结 语
针对现有配准算法在大批量点云配准效率低、配准误差大,容易受噪声的干扰的问题,提出了ISS算法精简点云,利用WHI描述符进行采样一致性算法完成点云粗配准,接着利用安德森算法加速ICP算法完成点云精确配准,与几种先进的算法做对比,实验表明所提的算法在3D扫描库场景中点云配准精度、配准速度都有不同程度的提高,在有噪声、离群点的室内、外场景算法依然可用,在工程实际中具有重要的意义。同时也存在不足,ISS算法参数设置复杂,需要人工干预,实验模型应在更多的场景中进行,这也是后期将要改进的地方。
