基于图像灰度的大范围辐射温度反演
2024-01-15孙子林
孙子林,李 科
(天津津航技术物理研究所,天津 300300)
1 引 言
红外热成像技术已经广泛应用于军事、航天、冶金、医疗、电力等领域,为获得目标物体实时表面温度提供了便捷、高效的方法。目前典型红外热成像系统接收辐射主要分为三种:目标辐射、背景辐射和环境辐射(主要为红外热成像系统自发辐射)[1-3]。背景辐射和环境辐射是影响红外热成像系统探测性能的重要因素,其主要影响体现在对系统噪声和输出灰度的增加。
事实上,红外热成像系统探测性能还受到多种其他因素制约,例如目标的发射率、反射率、大气透射率、气流稳定性、镜头温度、系统电路变化等。目前,很多学者在提高红外测温领域做出了贡献,如李云红等人研究了物体表面发射率和背景温度对红外测温的影响;张志强等人研究了灰度值与被测物体温度的匹配模型,提出了一种精确标定测温曲线的方法;杜玉玺等人研究了探测目标的距离对不同强度热源红外测温影响及补偿:张艳超等人对影响测温精度的镜筒辐射温度、探测器靶面温度以及热像仪工作累积时间三个因素进行评估和建模;周康康等人研究了基于红外热图像灰度的修正模型[4-9]。
红外热成像高精度测温技术影响因素众多,修正模型较为复杂,一直是国内外学者研究的热点[10-14],上述文献中基本都是针对某一要素进行分析研究。本文从能量变换的角度出发,研究了探测目标温度、镜头温度、积分时间这三个方面对热像仪输出灰度值的共同影响,以图像灰度值进行反演计算探测目标的温度,最后进行验证分析。
2 红外热像仪能量传递模型
通过黑体辐射理论进行数据标定,在特定距离和积分时间下,计算不同温度黑体在不同镜头温度下传输到成热像仪的温度,并生成黑体辐射温度与热像仪输出灰度值拟合曲线。
由普朗克黑体辐射定律和斯蒂芬-玻尔兹曼定律可知黑体的在半球内的总辐射亮度如下式:
(1)
式中,第一辐射常数:
c1=3.7418×10-16(W·m2);
第二辐射常数:
c2=1.4388×10-2(m·K);
斯蒂芬-玻尔兹曼常数:
由于红外热像仪一般工作在特定范围的波段,为了确定这一范围内的辐亮度,对黑体光谱辐射度进行特定波段内的积分:
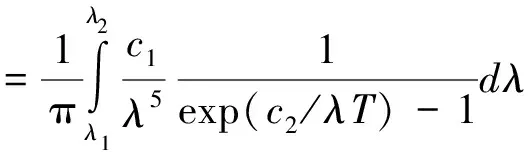
(2)
不同波段内黑体辐射亮度积分图像如图1所示,可以直观看出,黑体的光谱辐亮度与黑体温度的关系在不同波段范围内有较大差异,当其工作在窄波段(4.2~4.45 μm)时,其曲线如图2所示,此时其关系可以近似用三次多项式来表述。

图1 不同波段黑体温度-辐亮度变化曲线
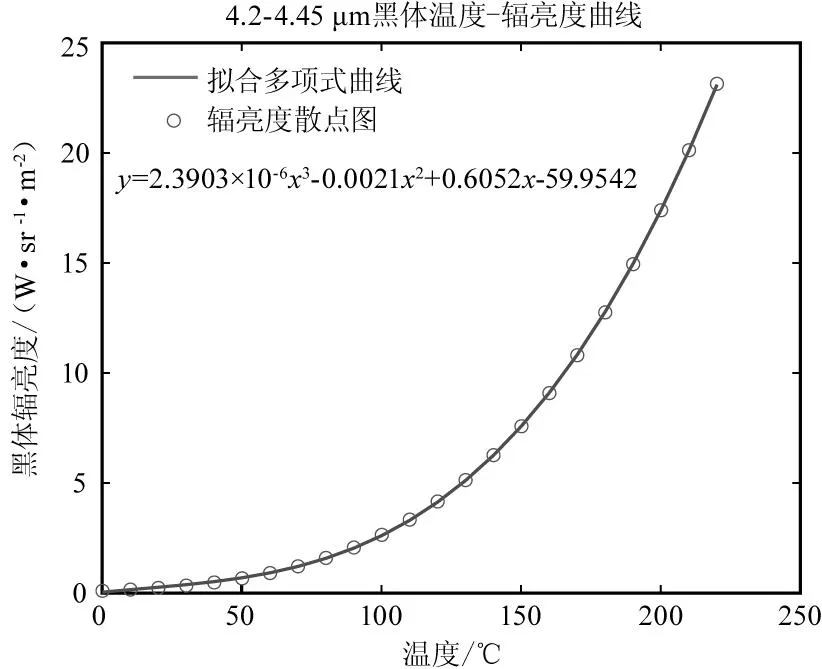
图2 窄波段黑体温度-辐亮度拟合曲线
对不透明物体,其表面总的辐亮度和作用于热像仪入瞳的辐射照度为:
Lλ=ελLbλ(T0)+ρλLbλ(Tu)
=ελLbλ(T0)+(1-αλ)Lbλ(Tu)
(3)
Eλ=A0d-2[ταλελLbλ(T0)+ταλ(1-αλ)·
Lbλ(Tu)+εαλLbλ(Ta)]
(4)
式中,ελ为表面辐射率;ρλ表面反射率;αλ为表面对环境辐射的吸收率;A0为热像仪最小空间张角对应目标的可视面积,d为该目标到测量仪器的距离;A0d-2通常在一定条件下为一个常值;ταλ为大气透过率;εαλ为大气发射率;Lbλ(T0)为辐射亮度;T0、Tu、Ta分别为被测物体温度、背景环境温度、大气温度。
探测器将工作波段的入射辐射进行积分,并把它转化成一个与能量成正比的电压信号,之后放大该信号,其放大倍数由系统本身决定,对应其不同量程。最终信号为:
Vs=K{τa[εIR(T0)+(1-aλ)IR(Tu)]+
(5)

由于红外热像仪接收的是目标的自身辐射、环境的反射辐射和大气辐射的总和,且三种辐射区分难度较大,通常假定其接收的辐射为某一黑体发射的辐射,因此将红外热成像指示的温度称为辐射温度或表观温度。令:
(6)
式中,IR(Tr)也称为红外辐射热像仪的刻度函数,通常是通过定标得到IR(Tr)与黑体温度的关系,则式(5)变为:
IR(Tr)=τa[εIR(T0)+(1-aλ)IR(Tu)]+εaIR(Ta)
(7)
在实验室条件下,环境辐射强度、路径辐射强度和大气成分变化程度等都较小,可以假定大气透射率τa=1,εa=0,且此时实验用辐射源为黑体,可以认为IR(Tr)=IR(T0),即热像仪测得的温度就是物体表面的实际温度。若ε<1,那么热像仪测得辐射温度和物体真实温度不一致。当认为被测物体为灰体且近距离测量时,热像仪测温修正计算基本公式如下:
IR(Tr)=εIR(T0)+(1-aλ)IR(Tu)
(8)
若红外成像系统是线性响应,则由式(3)可得其辐射响应灰度模型在实验条件下如式(9)所示[14-16]:
Y=tG1L(Tb)+tG2Lout+tKt+Ddark
(9)
式中,L(Tb)为目标的辐射能量;Lout为杂光干扰,一般情况下可视为镜头温度Topitc的函数;Ddark暗电流引起的响应偏移;t为积分时间。
3 基于多项式拟合的辐射反演模型
实验可知,探测目标温度不变,图像灰度值随着镜头温度的升高而升高,且在窄波段,黑体温度和辐亮度关系可以近似为:
Mb(λ1~λ2)(T)≈CTn
(10)
当其工作在在2~5 μm波段,n=9.2554;在8~13 μm波段,n=3.9889。实际应用中,高次方程不易求解,故可用泰勒公式将其展开为三次多项式再进行求解。
在镜头温度不变条件下,对黑体辐亮度在窄波段内进行积分,如图3所示。可以看出,在不同积分时间下图像灰度值与黑体辐亮度近似为线性关系。由于黑体辐亮度与黑体温度的关系可以用三次多项式进行近似,故黑体温度和图像灰度值也可以近似用三次多项式表示。在不考虑积分时间的影响下,综合实验数据,得出如下温度反演公式:
(11)

图3 不同积分时间下的红外图像灰度值与黑体辐亮度关系图
式中,Tj为探测目标温度;y为图像灰度值;Toptic为镜头温度;a1、a2…a6为优化参数。
求取参数之后便可以建立黑体温度与图像灰度值的多项式方程,之后带入图像灰度值和镜头温度便可以反演求得该探测目标的实际温度。由于热像仪的构造不同,在实际工程应用中,应先对该热像仪进行数据标定,之后才可使用灰度值进行反演计算。
4 试 验
红外热像仪由于制作工艺和本身性质决定了焦平面阵列上各个像元接收探测目标辐射能量的一致性较差,需要进行非均匀校正和温度定标,确保各个像元测温的准确性。温度定标实验采用高精度面源黑体近距离测温,此时认为黑体发射率及大气透过率近似为1,可以忽略其影响,认为测量温度便是黑体设定温度。
定标实验时,设置面源黑体的温度依次递增,每次温度稳定之后,在面源黑体的中心划定一块中心区域,录制100帧该区域内各个像元的灰度图像。对100帧图像各个像元的灰度值分别取平均值,再将区域内所有像元灰度值取平均值,并以该值为此黑体温度对应的灰度值。记录相同黑体温度不同镜头温度下各个积分时间热像仪灰度值的变化,进行多项式参数计算。最后根据图像灰度值反演探测目标温度。
在实验室条件下,保持实验室温度、探测距离等因素不变,以Toptic=28 ℃为例,分别对不同积分时间进行求参,拟合曲线如图4所示。
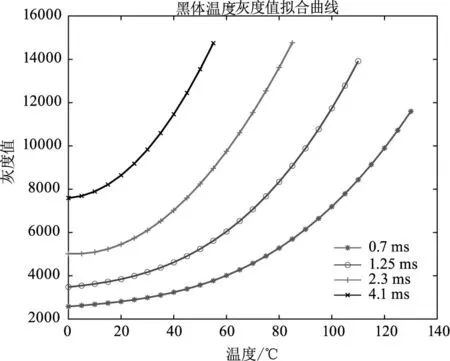
图4 不同积分时间下黑体温度-灰度值拟合方程曲线
将另一面源黑体作为目标,依次设置目标温度为30 ℃,35 ℃,分别基于热像仪直接测温和基于辐射反演模型测温,由于探测目标为黑体,可以近似认为黑体设定温度便是其辐射温度。
在Toptic=28 ℃条件下,分别对不同积分时间进行求参,计算结果如表1所示。
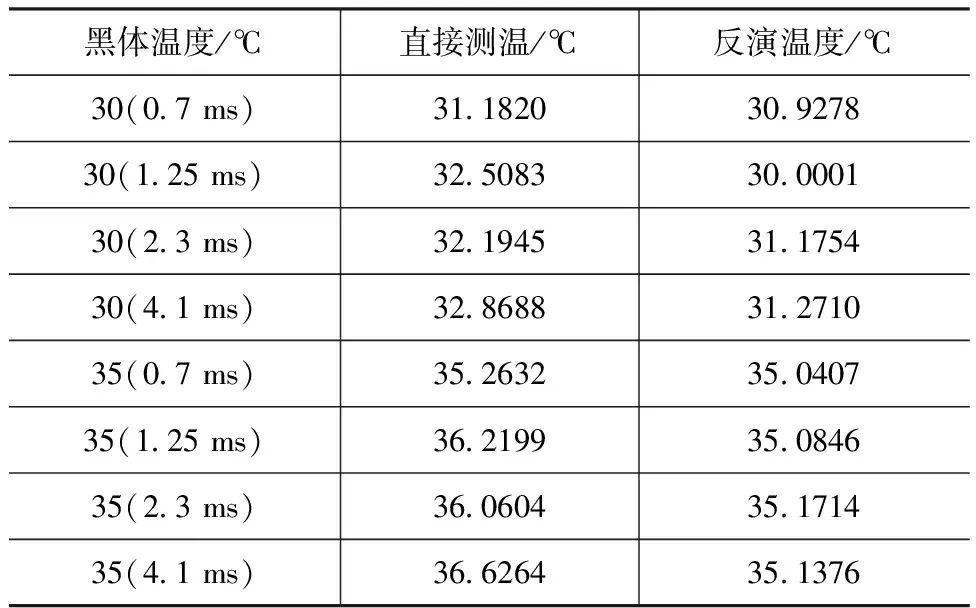
表1 温度反演实验数据
从表1可以看出,基于图像灰度的反演温度要比热像仪直接测得的温度精度要高。由于热像仪本身性质决定,其本身输出灰度值有一定阈值,当灰度值输出偏高接近阈值时,其对物体的测量误差也会偏大,本文的反演方法可以有效降低该误差。
5 小 结
本文提出的基于红外图像灰度并结合全环境温度、全目标温度、全积分时间的恒定数据量、高适应性辐射温度反演模型,通过对辐射测温原理的分析提出了反演多项式,该模型实现了环境(镜头)温度与场景温度参量解耦,降低了环境温度和积分时间对测温的影响。通过在实验室环境下的温度测量和分析,结果表明,该反演模型精度较热像仪测温更高,是一种提高测温精度的行之有效的方法。
