输电线路偶发性覆冰厚度预测及增强恢复力方法研究

李小双，曹阳，彭小峰，高会翔，王鑫

输电线路偶发性覆冰厚度预测及增强恢复力方法研究

李小双，曹阳，彭小峰，高会翔，王鑫

（重庆理工大学 电气与电子工程学院，重庆 401320）

针对输电线路发生偶发性覆冰时，线路覆冰预测精度低以及线路恢复力评估模型不准确等问题，首先根据灰色关联度比重，建立了基于分段粒子群优化（Partition particle swarm algorithm，PPSO）最小二乘支持向量机（Least squares support vector machine，LSSVM）的输电线路覆冰厚度预测模型，用于预测未来36 h的覆冰厚度。将线路覆冰后恢复力模型划分为覆冰前期、覆冰中期、覆冰恢复自持期、覆冰恢复后期4个阶段，分别建立评估指标；基于覆冰后线路功率变化熵和预测的线路覆冰增长量，建立线路韧性增强方式。仿真结果表明，采用所提方案后，传输系统在发生偶发性线路覆冰时的韧性被提高了11.54%。

输电线路；覆冰预测；恢复力评估；韧性增强；粒子群算法

0 引言

输电线路设计标准在非冰灾区和冰灾区的不同，以及偶发性冰灾所具有的短期和小范围特点，导致了非冰灾区域在发生偶发性输电线路覆冰时比冰灾区更有可能发生线路过载、断路器跳闸、导线舞动、绝缘子闪络、导线断线、塔杆倒塌以及电力通信中断等事故[1]。特别是一些重要的输电线路跨越地域广，线路所经地形复杂[2]，所以在极端恶劣天气下出现的偶发性覆冰灾害时，人工巡线的难度大。对输电线路覆冰进行可靠的预测并对其自恢复能力进行研究，可为电力部门制定调度、融冰、运维决策提供帮助[3,4]。

按照覆冰形成的物理和气象过程，输电线路覆冰可分为雨凇、雾凇、软雾凇、混合凇、湿雪5种。在这5种覆冰类型中，雨凇的密度最大，附着力最强，对输电线路的危害也是远远大于其他类覆冰[5-7]。目前，国内外学者已在输电线路覆冰厚度的预测上做过大量研究。

关于输电线路覆冰厚度的预测模型主要有物理理论模型、统计学模型及机器学习模型。

物理理论模型。文献[8]为提升基于动态拉力与倾角的架空输电线路覆冰力学模型的精度，提出了以导线动态拉力和倾角为输入、等值覆冰厚度为输出的多输入单输出耐张塔覆冰监测模型。文献[9]对线路覆冰进行力学分析，考虑不均匀载荷和风偏平面载荷，建立了输电线路综合荷载的等值覆冰厚度预测模型。由于物理理论模型中的某些力学参数在常规线路监测中难以获得，所以其在实际应用受到诸多限制。

统计学模型。文献[10]通过统计学原理分析了输电线路覆冰数据，得到了输电线路覆冰数据的特征和聚集类型。由于在应用时需要满足诸多统计假设条件，且线路周边微气象因素难以计及，所以统计学模型预测精度受到影响。

机器学习模型。文献[11]用灰色支持向量机建立了覆冰厚度短期预测模型。文献[12]利用覆冰增长的物理过程选取实际可测量的气象参数，并将其作为覆冰影响因素；对粒子群算法进行改进，使其在迭代过程中出现概率性变异；最终用优化BP（Back propagation）神经网络对覆冰厚度进行了预测。利用大量的覆冰监测数据对网络进行训练，是用机器学习算法对覆冰厚度进行预测的前提。监测数据包括温湿度、气压、风速、导线倾角、导线载荷等。目前，输电线路覆冰监测设备还有待完善，且大部分地区一年中覆冰时间不长，所以能采集到的数据量偏少。

针对极端自然灾害，文献[13]将潮流、概率风险评估和自适应能力分析相结合，提出了电力系统韧性和可靠性增强方法。文献[14]采用防御孤岛的方法提高电力系统在极端自然灾害下的恢复能力。为实现台风灾害下岛屿微电网群恢复能力的全过程提升，文献[15]提出了灾前储能调度、灾中的最优负荷削减和故障线路修复序列的灾后优化策略。文献[16]将脆弱性曲线的概念用于评估组件的故障概率，并根据天气和时间评估电力系统关键基础设施在极端自然灾害下的恢复能力。

为解决输电线路在发生偶发性覆冰时，覆冰厚度预测精度低和线路的恢复力评估模型不准确等问题，本文根据覆冰时线路所处环境的微气象数据变化特性，提出一种基于PPSO-LSSVM的输电线路覆冰厚度预测模型。将线路覆冰后恢复力模型分为覆冰前期、覆冰中期、覆冰恢复自持期、覆冰恢复后期4个阶段分别建立评估指标；基于覆冰后线路功率变化熵和预测的线路覆冰增长量，给出线路韧性增强方案。

1 输电线路覆冰预测

1.1 最小二乘支持向量机

最小二乘支持向量机算法是支持向量机（Support vector machine，SVM）算法的改进优化版本。利用最小二乘损失函数和等式约束，可将SVM的不等式变为等式，进而对SVM的二次规划问题加以简化[17,18]。LSSVM算法在小样本数据的预测中比BP神经网络等算法更具优势。

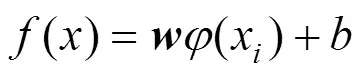
式中：为偏置位；为权值向量。

根据经验风险最小化原理，LSSVM回归变为约束优化：

引入拉格朗日函数求解优化问题：

式中：a为拉格朗日乘子。

根据非线性规划（Karush-Kuhn-Tucker，KKT）条件和Mercer原理，可得到线性方程组如式（4）所示。

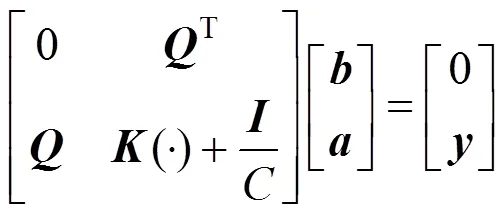
根据最小二乘法求解式（4），并采用RBF核函数，使LSSVM具有更好的泛化能力，得到回归函数：

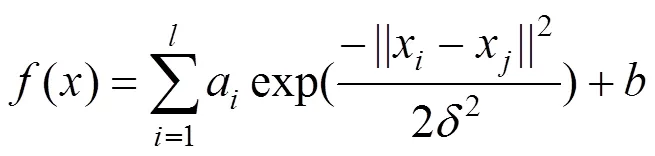
式中：为RBF核函数宽度。

惩罚因子和核函数参数是LSSVM模型的重要参数。这2个参数的合适与否将直接影响模型拟合效果。因此，为提升LSSVM的拟合效果，需对和进行寻优。输入变量根据灰色关联度分析结果进行选择。

1.2 分段粒子群优化算法

粒子群算法模拟了鸟群在起飞时的信息交互过程，通过模拟鸟群之间的相互学习和模仿，寻找全局最优点[19,20]。

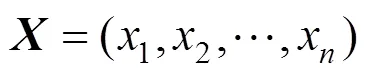
第代的第个微粒在第维空间（1≤≤）的速度更新公式如下：

第个粒子的位置更新公式如下：

粒子群算法原理简单、可实现度高、参数少，但其在寻优过程中容易陷入局部最优，且在高维空间和非线性函数求解时，其搜索精度较低、收敛速度较慢。

为提升PSO（Particle swarm optimization）算法的寻优效果，提出一种分段粒子群优化算法PPSO——将PSO算法分为前期、后期2个阶段，前、后期的迭代区间以划分。

在PSO算法中，要求粒子速度v在前期保持一个较大的值，从而提高算法的全局搜索能力；在后期，粒子速度应保持一个较小的值以提高局部搜索能力[21]。

通过2阶段动态控制策略并引入加减速系数改变粒子在迭代前后期的速度。改进后的粒子速度公式变为：

式中：>1为压缩因子；≥1为加速系数；≤0为减速系数；为迭代次数；为2阶段迭代次数区间，取总迭代次数的60%。

合理分配惯性权重有利于提升PSO算法在全局和局部的搜索能力。在搜索后期，恒定的惯性权重会导致局部搜索能力大幅下降。线性递减权重策略虽提高了局部搜索能力，但进入搜索后期时其值很小，易导致算法陷入局部最优解，使全局搜索能力下降[22]。

2阶段非线性惯性权重策略改变了算法在全局和局部的搜索能力。各阶段惯性权重为：

PPSO算法在搜索前期拥有更好的全局搜索能力，在后期具有更佳的局部搜索能力。算法始终处于高效搜索状态下，求解精度更高。

1.3 预测模型

输电线路覆冰现象由多种气候因素共同作用导致。针对线路覆冰要考虑的因素包括覆冰时长、环境温湿度、风速、光照强度等。输电线路运行地域分布广阔、运行环境复杂不稳定[23]，这导致其覆冰数据难以及时大量获取。样本数据的严重不足，将致使覆冰预测效果不佳。

针对小样本数据的预测问题，本文所采用具有很大的优势的LSSVM模型。

输电线路覆冰预测模型计算流程如图1所示。

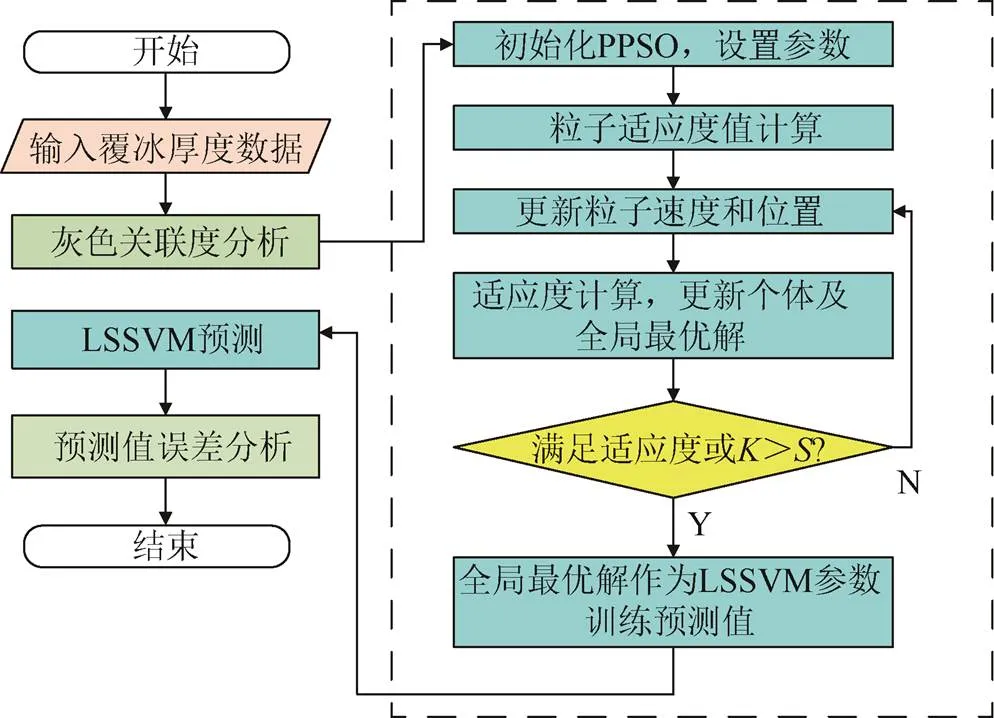
图1 输电线路覆冰预测模型计算流程

图1的总体思路：先对原始覆冰数据进行灰色关联度分析，利用PPSO算法进行参数寻优，确定LSSVM的和参数；再利用灰色关联度值排名前三的影响因素作为输入数据集，并根据覆冰数据集对未来36 h覆冰厚度进行预测。

具体计算步骤如下。

步骤1）根据灰色关联度分析各因素对覆冰的影响，取权重最大的前3个作为样本数据，将数据集划分为训练集和测试集。

步骤2）初始化LSSVM参数。设置为100、为1.5，划定C和的寻优范围。根据初次迭代结果采用均方差（MSE）作为适应度函数，公式如下：

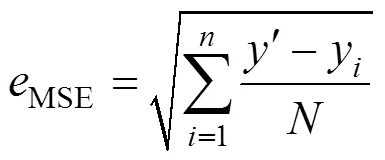
式中：为样本总量；¢为覆冰厚度预测值；y为覆冰厚度实际值。

步骤3）设置PPSO算法的参数。令：空间维数为2；种群规模为50；惯性权重随分段函数非线性递减，惯性权重最大值max和最小值min分别为0.95和0.30；最大迭代次数为100；加速系数为1.4；减速系数为–1.7；加速因子1、2均为2。

步骤4）将和作为粒子，并设置当前粒子最优解为100，为1.5。根据步骤2）计算各粒子的适应度值p。然后，每次迭代都用式（8）、式（9）更新粒子位置和速度，并得到一组新的和值。

步骤5）将步骤4）的最优解赋给LSSVM预测模型进行训练，并计算新的适应度P+1。

步骤6）对比P+1与P。若P+1优于P，则将P+1作为P；否则不变。

步骤7）判断是否达到算法终止条件，即P值最佳或算法迭代次数达到。若结果为是，则输出最优的和值；否则重返步骤4），继续迭代。

步骤8）将步骤7）的最优解赋给LSSVM预测模型，即可得到预测的覆冰厚度。

1.4 算法验证

以西南某110 kV线路二月7 d的线路覆冰在线监测装置实测数据算例，对算法进行验证。令采样间隔为3 h，共得到99组样本数据，部分数据样本如表1所示。将表中1—86号样本数据作为训练集，87—99号数据作为测试集。

预测12个点的覆冰厚度并检验模型的精度。采用均方根误差（RMSE）和平均相对误差（MRE）进行误差对比分析。

表1 部分覆冰数据样本

在MATLAB 2021a环境下，分别建立PPSO- LSSVM、PSO-LSSVM、BP-LSSVM预测模型。

采用SPSSPRO工具箱的灰色关联度分析模块分析影响覆冰厚度的主要因素。各影响因素灰色关联度系数计算结果如表2所示。由表2可知，环境温度、环境湿度以及环境风速的灰色关联度最高，也即这3个因素对导线覆冰的影响最大，故以此3个因素作为LSSVM模型的输入量。

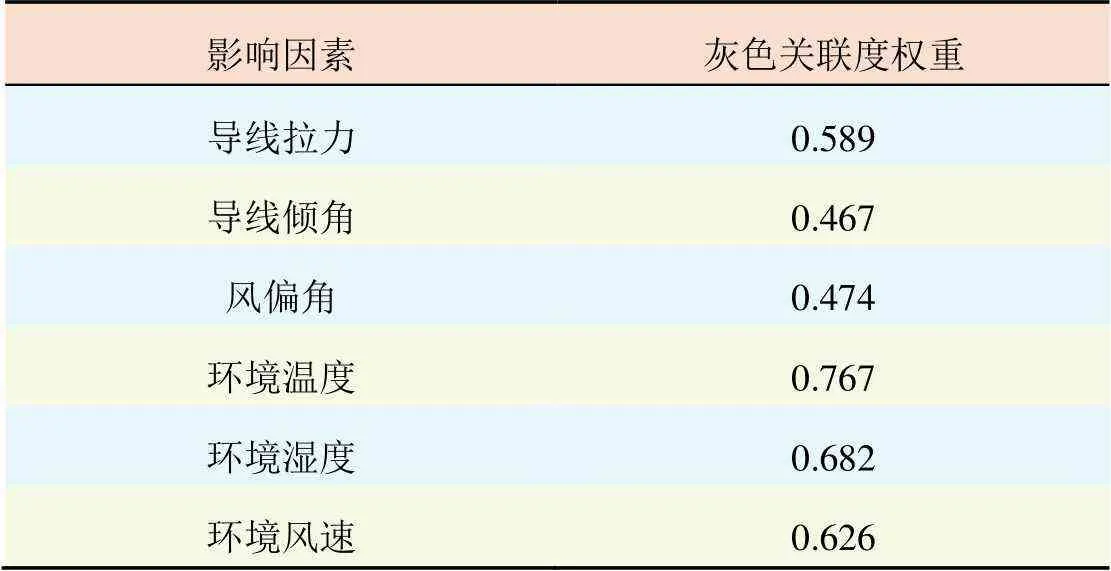
表2 各影响因素的灰色关联度系数

LSSVM模型的惩罚因子和核函数参数的选择对提高预测过程的速度和预测精度至关重要。为确定最佳的模型参数、构建更为准确的覆冰厚度预测模型，本文分别采用PPSO算法、PSO算法以及BP算法对LSSVM模型进行寻优。3种模型对LSSVM参数寻优的迭代曲线如图2所示。

由图2可知，相比PSO算法和BP算法，PPSO算法在寻优过程中具有更快的收敛速度、更低的精度损失。PPSO算法寻优能力更强，说明本文对PSO算法的改进起到了积极的作用。

图2 3种模型对LSSVM参数寻优迭代曲线

PPSO-LSSVM模型优化后的最佳参数为=110.74、2=52.41；PSO-LSSVM模型的最佳参数为=99.12、2=45.72；BP-LSSVM模型采用BP神经网络优化后的参数=97.27、2=42.53。

3种算法的训练结果如图3所示。

图3 3种模型训练结果

由图3可知，3种预测模型的训练拟合效果与实际覆冰厚度数据的增减趋势相符。

3种模型训练后的拟合度及误差评价结果如表3所示。

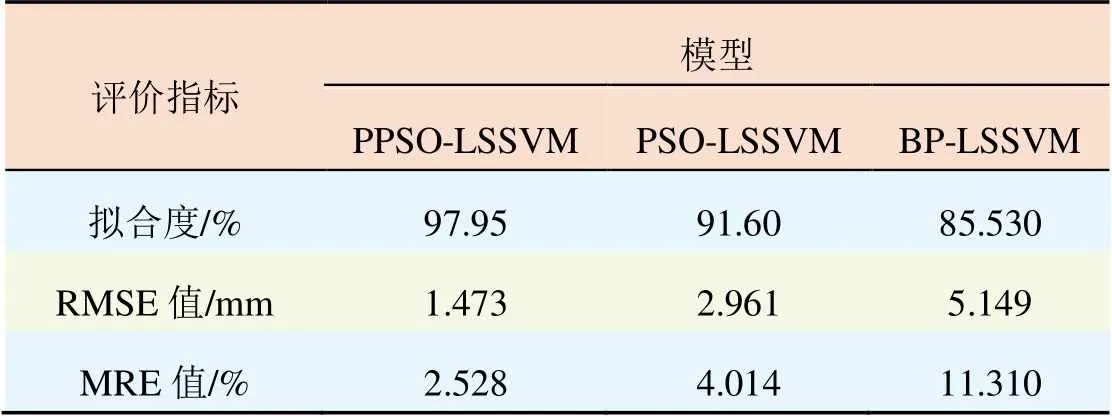
表3 3种模型训练后的拟合效果评价

由表3可知，PPSO-LSSVM模型的训练效果拟合度为97.95%、均方根误差为1.473 mm、平均相对误为差2.528%，均优于其他2种模型。

由上述结论可知对PSO算法的粒子速度和权重分段优化进一步提升了PPSO-LSSVM模型在覆冰厚度方面的预测能力和精度。

利用3种模型对12组测试集数据进行预测，预测结果如图4所示。

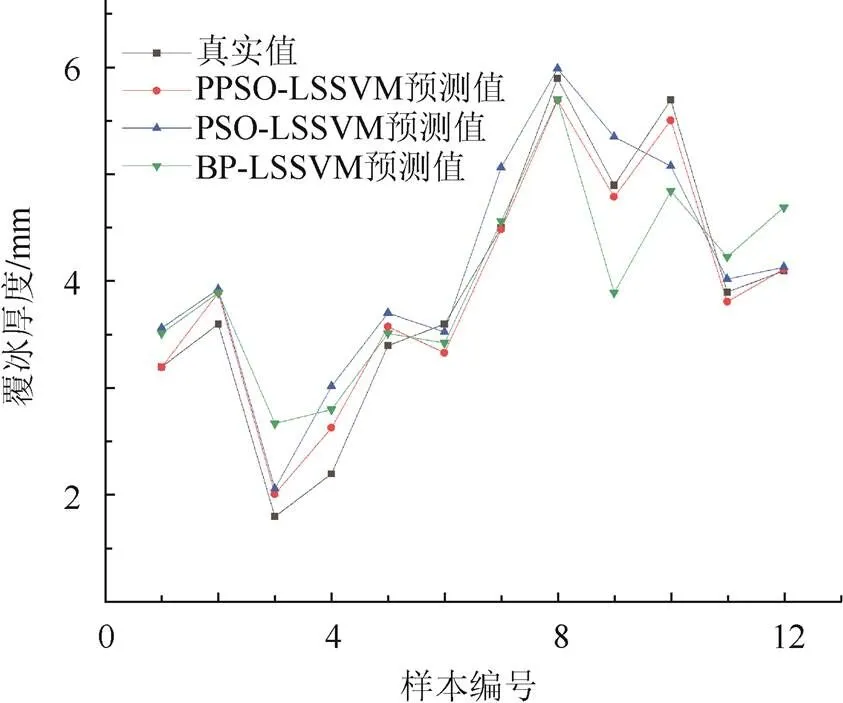
图4 3种模型预测结果

由图4可知BP-LSSVM模型的表现最差，PSO-LSSVM表现稍好，PPSO-LSSVM模型表现最佳。

3种模型预测误差如表4所示。

由表4可知，在利用PPSO-LSSVM模型进行预测时，RMSE和MRE值分别为1.209 mm、2.714%。可见，相比之下，利用PPSO-LSSVM模型可以大幅提高预测模型的精度。

表4 3种模型预测误差

精准的输电线路的覆冰厚度预测，将使后续关于线路覆冰增长量的预测更为精准。

2 输电系统恢复力增强

2.1 输电系统故障率模型

输电线路上冰层厚度的增长量ice使用由PPSO-LSSVM预测模型所预测得到的线路覆冰厚度。

单位长度线路的冰载荷I可根据ice进行计算。

式中：为导线直径。

单位线路长度风载荷W为：

式中：为风载体型系数；为跨度系数。

当导线直径在17 mm以内时，取1.2；当导线直径大于17 mm时，取1.1。

风载荷和冰载荷共同作用下的综合载荷IW为：

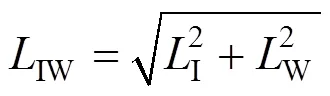
单位长度传输线的故障率f为[24]：

式中：IW和IW分别为冰荷载和风荷载的线阈值。

在多数情况下，输电线路的修复时间与覆冰的严重程度呈正相关，故在计算这2个阈值时可设置相同的时间。

线路恢复周期rep的计算公式如下：

式中：nmax分别为正常天气条件下线路的维护时间和最大维护时间；IW和IW分别为因求线路的维护时间而设置的2个阈值。

2.2 线路恢复力指标

偶发性冰灾和长期性冰灾作用在输电线路上时都是需要一定的时间累计。当冰灾发生时，输电线路不会立即失能。线路覆冰时的线路韧性曲线如图5所示。

图5 输电线路覆冰时韧性曲线

图5中，纵坐标代表了覆冰厚度，F0()是线路未覆冰时的韧性曲线，F()是输电线路在覆冰时的韧性曲线。在1时刻，线路开始覆冰，2时刻线路开始逐渐失能。1—2阶段是覆冰开始到传输性能开始下降的时段，其值反映了输电线路在覆冰时的自我抵抗力，且仅与线路设计参数相关。在3—4时段，线路进入停运状态，可能发生不可自恢复故障。在4—5时段，线路开始逐渐恢复，且恢复状态可维持线路运行。在5—6时段，线路处于恢复相持状态。在6—7时段，线路恢复到正常运行状态。

基于图5中恢复力评估曲线构建输电线路的韧性评估指标。为反映输电系统在不同覆冰阶段的性能、衡量其在出现偶发性覆冰时的恢复力，评估指标由覆冰前、覆冰中、覆冰恢复相持期、覆冰恢复后期4个阶段构成。综合韧性指标由这4个阶段的加权得到。

1）覆冰前评估指标re。

该指标可以反映输电线路的抗冰能力。

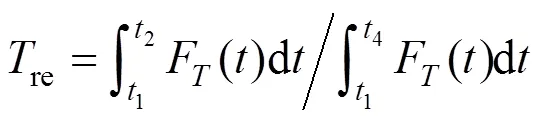
2）覆冰中评估指标Loss。

该指标可评估线路覆冰下线路性能损失的严重程度，并反映输电线路在覆冰时的鲁棒性。覆冰中期评估指标的值与输电线路的恢复能力呈负相关。

3）覆冰恢复相持期评估指标pr。

该指标可以评估覆冰后输电线路恢复情况的优劣，其值与输电线路的恢复能力呈正相关。

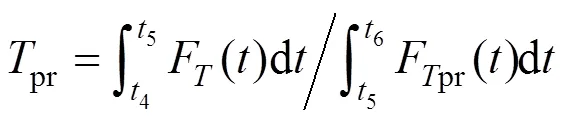
4）覆冰恢复后期评估指标rce。

该指标用于评估输电线路的恢复率。覆冰恢复后期评估指标值与输电线路的恢复率呈正相关。

式中：c–min为输电线路的恢复率的基值，即输电线路的理论最快恢复率。

覆冰前、覆冰中、覆冰恢复相持期、覆冰恢复后期恢复能力评估指标的值分别在0和1之间。对上述4个韧性评估指标进行加权，以获得综合韧性评估指标：

式中：re、Loss、pr和rce分别为覆冰前、覆冰中、覆冰恢复相持期、覆冰恢复后期恢复能力评估度量的权重系数，分别取值为0.2、0.4、0.2和0.2。

权重系数取值的考量：影响覆冰前指标的主要因素是线路的抗冻性和覆冰强度，而与系统自我调节和应急响应能力的关系主要体现在系统故障后的部分。加权因子的值可以针对不同的系统和不同的实际条件而改变。

2.3 恢复力增强方法

偶发性输电线路覆冰可能会影响传输系统的正常运行。

采用输电系统功率的变化熵值表示输电系统的运行状态，并确定线路主动除冰时输电系统的当前状态。

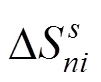
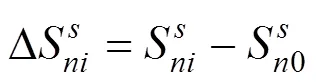
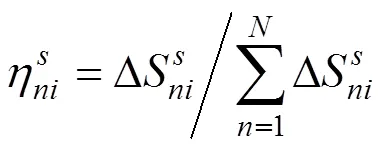
式中：为传输系统中的线路数量。

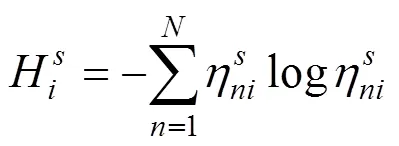
为增强输电系统在偶发性覆冰灾害下的韧性，本文通过预测线路上的覆冰厚度增长来选择除冰关键线路，并选用直流融冰法用于甩负荷和除冰。具体流程如下：

步骤1）输入线路实际数据和线路周边微气象数据，选择可能发生覆冰的线路，组成覆冰线路合计ice。

步骤2）采用预测模型预测，选ice的覆冰增长厚度，并计算除冰对输电系统负荷的减少量。减负荷模型参考文献[25]。

步骤3）根据式（21）—（23）获得覆冰线路负荷的变化熵，并结合步骤1）中集合导出关键覆冰导线。

步骤4）确定关键线路的覆冰厚度。若覆冰厚度接近设计值，则执行步骤5）；否则返回步骤2）。

步骤5）断开所选关键线路进行除冰，通过甩负荷模型获得系统负荷的变化。

步骤6）计算输电线路的韧性度和线路韧性程度的变化。

2.4 模型验证

以图6所示IEEE-30总线传输系统为算例，验证本文提出的恢复力评估方法的合理性和恢复力增强方法的有效性。图中显示了传输系统节点的地理位置和线路覆冰的大致覆盖范围。采样时间间隔为20 min。

图6 IEEE-30总线传输系统地理网格

从图6可以看出，偶发性线路覆冰只影响气象范围内的线路。

图7显示了传输系统中每条线路的故障率。线路覆冰需要一定的时间才能导致输电系统的传输性能下降或发生故障，因此图7只给出了在采样点序85—120范围内的故障率，其余时间输电系统没有减负荷。

图7 各线路故障率

表5显示了在除冰时用本文方法得到的对关键线路的选择结果。由表5可知，在线路中断期间，功率流传递熵最大的线路是14-15号线。主动停机除冰导致了系统负载少量下降，其值低至26.36 kV·A。

表5 输电系统负荷增长量及变化熵

根据输电系统的负荷增强的高低筛选除冰关键线路。根据表5选择5-22号线为除冰关键线路。

采用蒙特卡洛方法获得48 h内每条线路运行状态的变化，再应用降负荷模型获得整个过程的负荷变化。除冰前后系统负荷曲线的变化见图8。

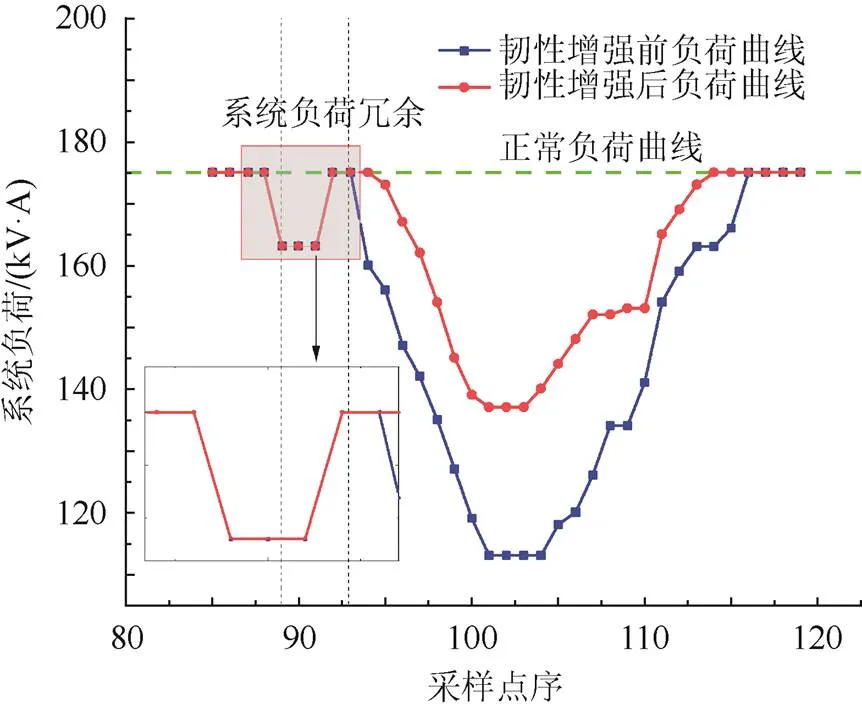
图8 输电系统除冰前后负荷变化

当线路覆冰开始加重时，输电线路本身机械强度以及绝缘强度等都会下降，从而导致该线路或该覆冰片区在调度或继保作用下出现负荷波动或者降低。如图8所示，选定的除冰关键线路在第87个采样点所在时刻关闭并除冰。由于传输系统的负荷冗余，传输系统的负载没有下降。通过使用所提出的韧性增强方法，可以显著减小传输系统的负载降低。

采取韧性增强策略后的恢复力评估指标结果如表6所示。

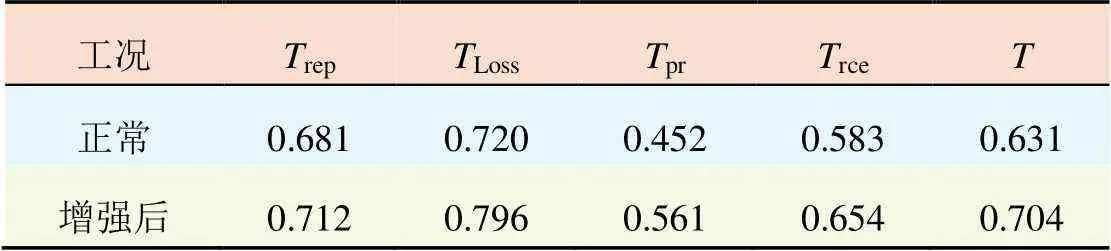
表6 恢复力评估指标对比结果

由表6可知，与采用本文策略情况相比，传输系统的覆冰恢复能力评估指标相对较小。这表明，输电线路传输系统的韧性相对较小。采用韧性增强方法后，输电系统在覆冰期间的总负荷减少量降低，所有恢复力评估指标都得到了相应的改进，综合恢复力评估指标提高了11.57%。

3 结论

为了解决偶发性输电线路覆冰时，线路覆冰预测低精度和线路的恢复力评估模型不准确等问题，提出了一种偶发性覆冰下输电线路覆冰预测及恢复力增强方法。仿真实验结果表明：

1）用基于PPSO-LSSVM的输电线路覆冰预测模型预测未来24 h的线路覆冰厚度，其预测值的均方根误差和平均相对误差分别为1.209 mm、2.714%，优于PSO-LSSVM、BP-LSSVM预测模型。

2）提出了覆冰前、覆冰中、覆冰恢复自持期、覆冰恢复后期的评估指标，分别对应输电线路的抗冰能力、性能损失程度、线路恢复情况的优劣以及线路恢复率。

3）通过覆冰时线路的功率变化熵选择除冰的关键线路，提高了线路抗冰能力、减小了输电系统减载，使综合恢复力得到提高，其有效增强了输电系统在偶发性覆冰时的运行韧性。

[1] 李昊, 曾彤, 陈晓国, 等. 覆冰在线监测预警系统研究现状分析[J]. 电气自动化, 2015, 37(2): 63-65. LI HAO, ZENG TONG, CHEN XIAOGUO, et al. An analysis on the research status of icing online monitoring and early warning system[J]. Electrical Automation, 2015, 37(2): 63-65(in Chinese).

[2] 邓红雷, 戴栋, 李述文. 基于层次分析-熵权组合法的架空输电线路综合运行风险评估[J]. 电力系统保护与控制, 2017, 45(1): 28-34. DENG HONGLEI, DAI DONG, LI SHUWEN. Comprehensive operation risk evaluation of overhead transmission line based on hierarchical analysis-entropy weight method[J]. Power System Protection and Control, 2017, 45(1): 28-34(in Chinese).

[3] 杨洪磊, 司兴登, 梁仕斌, 等. 北斗导航定位系统在架空输电线路覆冰监测中的应用研究[J]. 电子元器件与信息技术, 2021, 5(3): 94-95.

[4] 郝艳捧, 王信媛, 梁苇, 等. 连续3天覆冰微气象数据驱动的架空输电线路覆冰类型识别与预测[J]. 南方电网技术, 2023, 17(6): 107-116. HAO YANPENG, WANG XINYUAN, LIANG WEI, et al. Ice types identification and prediction of overhead transmission lines driven by micro-meteorological data of three consecutive days icing[J]. Southern Power System Technology, 2023, 17(6): 107-116(in Chinese).

[5] 张暕. 架空输电线路覆冰机理及预测模型的研究[D]. 北京: 华北电力大学, 2019. ZHANG JIAN. Research on mechanism and prediction model of icing on overhead transmission lines[D]. Beijing: North China Electric Power University, 2019(in Chinese).

[6] 沈锋, 艾永俊, 周朝荣, 等. 输电线路防冰及除冰技术研究现状[J]. 云南电力技术, 2023, 51(1): 18-22. SHEN FENG, AI YONGJUN, ZHOU CHAORONG, et al. Research status of transmission line anti-icing and de-icing technology[J]. Yunnan Electric Power, 2023, 51(1): 18-22(in Chinese).

[7] 王勇, 苗虹, 莫思特, 等. 高压架空输电线路防冰、融冰、除冰技术研究综述[J]. 电力系统保护与控制, 2020, 48(18): 178-187. WANG YONG, MIAO HONG, MO SITE, et al. Summary of research on anti-ice, ice melting and de-icing of high voltage overhead transmission lines[J]. Power System Protection and Control, 2020, 48(18): 178-187(in Chinese).

[8] 张松海, 施心陵, 李鹏, 等. 基于动态拉力与倾角的输电线路覆冰过程辨识与建模[J]. 电力系统保护与控制, 2016, 44(9): 57-61. ZHANG SONGHAI, SHI XINLING, LI PENG, et al. Identification and modeling of the power transmission line icing based on dynamic data of tension and angle[J]. Power System Protection and Control, 2016, 44(9): 57-61(in Chinese).

[9] 张乐, 周步祥, 王小红, 等. 导线覆冰监测系统的力学模型与预警功能优化[J]. 电力系统及其自动化学报, 2014, 26(11): 42-46. ZHANG LE, ZHOU BUXIANG, WANG XIAOHONG, et al. Mechanical model of transmission line icing monitoring systems and optimization of alarm function[J]. Proceedings of the CSU-EPSA, 2014, 26(11): 42-46(in Chinese).

[10] 王敩青, 戴栋, 郝艳捧, 等. 基于在线监测系统的输电线路覆冰数据统计与分析[J]. 高电压技术, 2012, 38(11): 3000-3007. WANG XIAOQING, DAI DONG, HAO YANPENG, et al. Statistics and analysis of transmission lines icing data based on online monitoring system[J]. High Voltage Engineering, 2012, 38(11): 3000-3007(in Chinese).

[11] 马小敏, 高剑, 吴驰, 等. 基于灰色支持向量机的输电线路覆冰厚度预测模型[J]. 中国电力, 2016, 49(11): 46-50. MA XIAOMIN, GAO JIAN, WU CHI, et al. Prediction model for icing thickness of power transmission line based on grey support vector machine[J]. Electric Power, 2016, 49(11): 46-50(in Chinese).

[12] 李贤初, 张翕, 刘杰, 等. 输电线路导线覆冰AMPSO-BP神经网络预测模型[J]. 电力建设, 2021, 42(9): 140-146. LI XIANCHU, ZHANG XI, LIU JIE, et al. Prediction of transmission line icing thickness applying AMPSO-BP neural network model[J]. Electric Power Construction, 2021, 42(9): 140-146(in Chinese).

[13] VAAGENSMITH B, MCJUNKIN T, VEDROS K, et al. An integrated approach to improving power grid reliability: merging of probabilistic risk assessment with resilience metrics[C]//2018 Resilience Week (RWS). Denver, CO, USA: IEEE, 2018: 139-146.

[14] PANTELI M, TRAKAS D N, MANCARELLA P, et al. Boosting the power grid resilience to extreme weather events using defensive islanding[J]. IEEE Transactions on Smart Grid, 2016, 7(6): 2913-2922.

[15] PANTELI M, MANCARELLA P. Modeling and evaluating the resilience of critical electrical power infrastructure to extreme weather events[J]. IEEE Systems Journal, 2015, 11(3): 1733-1742.

[16] 赵宁远. 冰灾下输电系统韧性评估与全时段韧性增强策略[D]. 天津: 天津大学, 2023. ZHAO NINGYUAN. Resilience assessment and full-time resilience enhancement strategies for transmission system under ice disaster[D]. Tianjin: Tianjin University, 2023(in Chinese).

[17] 陈勇, 李鹏, 张忠军, 等. 基于PCA-GA-LSSVM的输电线路覆冰负荷在线预测模型[J]. 电力系统保护与控制, 2019, 47(10): 110-119. CHEN YONG, LI PENG, ZHANG ZHONGJUN, et al. Online prediction model for power transmission line icing load based on PCA-GA-LSSVM[J]. Power System Protection and Control, 2019, 47(10): 110-119(in Chinese).

[18] 孔敏儒, 陈怡, 李文慧, 等. 基于粒子群优化PCA-LSSVM算法的高压断路器机械故障诊断研究[J]. 电网与清洁能源, 2019, 35(10): 68-74. KONG MINRU, CHEN YI, LI WENHUI, et al. Research on mechanical fault diagnosis of high voltage circuit breakers based on particle swarm optimization PCA-LSSVM[J]. Power System and Clean Energy, 2019, 35(10): 68-74(in Chinese).

[19] 潘晨, 滕欢, 梁梦可, 等. 基于改进粒子群算法考虑阀点效应的经济负荷最优分配[J]. 电力科学与技术学报, 2020, 35(1): 151-156. PAN CHEN, TENG HUAN, LIANG MENGKE, et al. Optimal distribution of economic load based on the improved particle swarm optimization considering valve-point effects[J]. Journal of Electric Power Science and Technology, 2020, 35(1): 151-156(in Chinese).

[20] 潘峰, 薛萍, 任翔宇, 等. 改进PSO-SVM工业防火墙白名单自学习方法研究[J]. 信息技术与网络安全, 2019, 38(6): 11-16. PAN FENG, XUE PING, REN XIANGYU, et al. Research on white-list self-learning method of industrial firewall with improved PSO-SVM[J]. Cyber Security and Data Governance, 2019, 38(6): 11-16(in Chinese).

[21] 曹阳, 钟烨, 彭醇陵, 等. 基于混合供能和能量协作的异构网络能量效率优化算法[J]. 通信学报, 2022, 43(3): 135-147. CAO YANG, ZHONG YE, PENG CHUNLING, et al. Energy efficiency optimization algorithm of heterogeneous networks based on hybrid energy supply and energy cooperation[J]. Journal on Communications, 2022, 43(3): 135-147(in Chinese).

[22] 郝少伟, 李勇军, 赵尚弘, 等. 基于改进粒子群算法的多载波NOMA 功率分配策略[J]. 电子学报, 2020, 48(10): 2009-2016. HAO SHAOWEI, LI YONGJUN, ZHAO SHANGHONG, et al. Multicarrier NOMA power allocation strategy based on improved particle swarm optimization algorithm[J]. Acta Electronica Sinca, 2020, 48(10): 2009-2016(in Chinese).

[23] 张国锋, 惠康, 务孔永, 等. 输电线路杆塔接地体的电流和能量负荷特性研究[J]. 电力学报, 2021, 36(6): 505-511. ZHANG GUOFENG, HUI KANG, WU KONGYONG, et al. Research on current and energy characteristics of transmission line tower’s grounding body[J]. Journal of Electric Power, 2021, 36(6): 505-511(in Chinese).

[24] LIN C, FANG D, BIE Z, et al. A reliability-based DG planning method against ice storm weather[C]//2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia). Chengdu, China: IEEE, 2019: 4002-4007.

[25] 赵书强, 涂筱莹, 王达飞, 等. 考虑负荷特性的输电网可靠性评估软件开发[J]. 电力自动化设备, 2014, 34(7): 129-133. ZHAO SHUQIANG, TU XIAOYING, WANG DAFEI, et al. Development of reliability evaluation software of power transmission grid[J]. Electric Power Automation Equipment, 2014, 34(7): 129-133(in Chinese).

Study on Prediction of Occasional Icing Thickness of Transmission Lines and Methods for Enhancing Resilience

LI Xiaoshuang, CAO Yang, PENG Xiaofeng, GAO Huixiang, WANG Xin

(School of Electrical and Electronic Engineering, Chongqing University of Technology, Chongqing 401320, China)

In order to solve the problems of low prediction precision of transmission line icing and inaccurate evaluation model of line resilience when occasional icing occurs on transmission line, firstly, according to the proportion of grey correlation degree, a icing thickness prediction model of transmission line is constructed based on partition particle swarm algorithm (PPSO) and least squares support vector machine (LSSVM) for predicting icing thickness in next 36 h. The resilience model is divided into four stages: pre-icing stage, mid-icing stage, self-sustaining stage and post-icing stage with creating evaluation index respectively. Based on the change entropy of line power after icing and the predicted increase of line icing, the enhancement mode of line toughness is established. The simulation results show that the proposed scheme improves the transmission system's toughness by 11.54% in the case of accidental line icing.

transmission lines; ice cover prediction; resilience assessment; toughness enhancement; particle swarm algorithm

10.3969/j.ISSN.1672-0792.2024.01.005

TM753

A

1672-0792(2024)01-0039-11

重庆市教委基金资助项目（KJ120827）。

2023-09-09

李小双（1997—），男，硕士研究生，研究方向为智能电网、传感器组网系统；

曹阳（1977—），男，教授，研究方向为智能电网和通信理论；

彭小峰（1980—），男，副教授，研究方向为无线电电子学；

高会翔（1999—），男，硕士研究生，研究方向为无线传输供能；

王鑫（1997—），男，硕士研究生，研究方向为输电线路PLC通信。

曹阳