具有自适应标定功能的施肥控制系统的设计与试验

万仕军，何瑞银，余洪峰，段庆飞，徐高明，孙国峻

(1 南京农业大学 工学院,江苏 南京 210031；2 江苏省智能化农业装备实验室,江苏 南京 210031；3 南京农业大学 人工智能学院,江苏 南京 210031)

化肥在农业生产中不可或缺[1]，科学合理地施用化肥能够有效提高作物的产量，而化肥施用不足或者过量会对农产品的产量、质量以及环境造成负面影响，因此需要精准施肥[2-6]。不同作物或者同种作物的不同生长发育阶段对营养元素需求不同。因此为了实现多种肥料的自适应精准控制，设计一种具有自适应标定功能的施肥控制系统具有现实意义。

若要实现精准施肥，需要对肥料排量进行精准控制[7]和建立准确的排量模型[8]。实现精准施肥的主要问题在于提升排量模型的准确性。为此国内外学者在排肥装置、排肥监测等方面进行了大量的研究[9-11]。一类是对排肥装置进行改进，提升施肥机械的准确性：控制电机通过自动调节外槽轮的工作体积控制施肥量，实现较大排肥量的精准控制[12]；改进常规的外槽轮排肥器，提升排肥器的稳定性与准确性[13-14]。这类方式可以提升施肥机械的准确性，但无法适应更换肥料种类带来的物理属性的变化，需要重新校准。另一类方式是对施肥量进行监测，通过闭环控制来提升排肥系统的准确性，但利用环形电极对肥料颗粒携带的电荷强度进行检测计算排肥速率[15]、采用图像识别对排肥流量进行监测[16]、通过电容的变化情况对施肥量进行在线监测[17]等方式也难以实现对不同种类肥料的自适应控制，在更换肥料种类时需要重新对传感器参数进行标定；有学者通过动态称质量的方式监测播量[18]，但该方式需要大量程、高精度的传感器，现有传感器难以兼容，并且田间作业时易受到震动的影响，显著影响机器的作业效率和作业质量。

本研究引入容积密度优化常规排量标定公式，在此基础上设计一种具有自适应标定功能的施肥控制系统，以期在肥料类型改变的情况下，仍能实现施肥量的精准控制。

1 自适应施肥控制系统结构及实现方式

1.1 系统结构

自适应施肥控制系统的总体结构如图1 所示，主要包括机架、肥箱、容积密度测量模块、链轮传动装置、直流减速电机和外槽轮排肥器等。

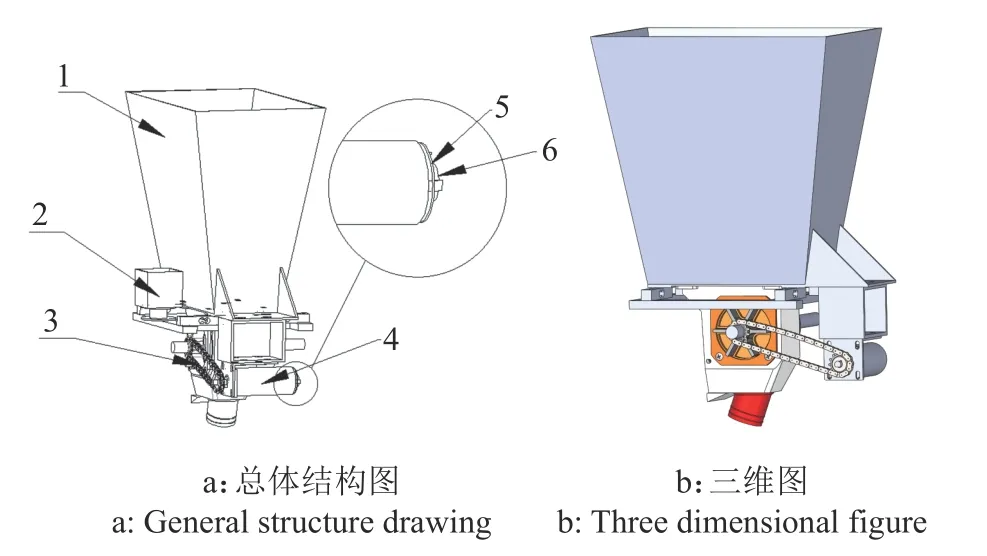
图1 自适应施肥控制系统结构示意图Fig.1 Structure diagram of adaptive fertilization control system

1.2 实现方式

施肥控制系统精度的关键影响因素是排量标定公式，目前施肥控制系统使用的标定公式每一次标定只适用于一种肥料。本研究引入容积密度，优化常规标定公式，使其能够一次标定适应多种肥料，以期为自适应施肥控制系统提供理论依据。

1.2.1 标定公式的优化 常规排量标定公式[19]和外槽轮式排肥器的排量计算公式为：

式中，v1为排肥轴转速，r /min；k为拟合曲线斜率；b为拟合曲线截距；Q为排肥流量，g/min；d为外槽轮外径，cm；L为槽轮的有效工作长度，cm；ρ为单位容积质量，g/cm3；α为填充系数，通过试验得出；f为单个凹槽的截面积，cm2；T为槽轮凹槽截距，cm；c为带动层系数，cm。

由式(2)可知，外槽轮排肥器的排量主要与排肥轴转速、外槽轮外径、槽轮的有效工作长度、单位容积质量、填充系数、单个凹槽的截面积、槽轮凹槽截距和带动层系数有关，其中，外槽轮外径、槽轮的有效工作长度、单个凹槽的截面积和槽轮凹槽截距由排肥机构的机械结构所决定。在合理的转速范围内填充系数与带动层系数的变化不大[12]，排量主要由转速和容积密度决定。常规排量公式只考虑转速，将容积密度作为固有属性。而不同种类肥料的容积密度不同，为了使标定公式适应多种肥料，引入容积密度(ρ')，并参考公式(1)、(2)，建立了新型标定公式(3)：

1.2.2 工作原理 自适应施肥控制系统工作原理如图2 所示，首先测量当前肥料的容积密度，读取排量信息，根据排量模型计算目标排肥转速；然后通过霍尔编码器监测电机转速，通过PID 算法输出对应的脉冲宽度调变(Pulse width modulation,PWM)信号，使用驱动器放大功率，从而精准控制电机转速，实现对各种肥料的自适应精准排量控制。

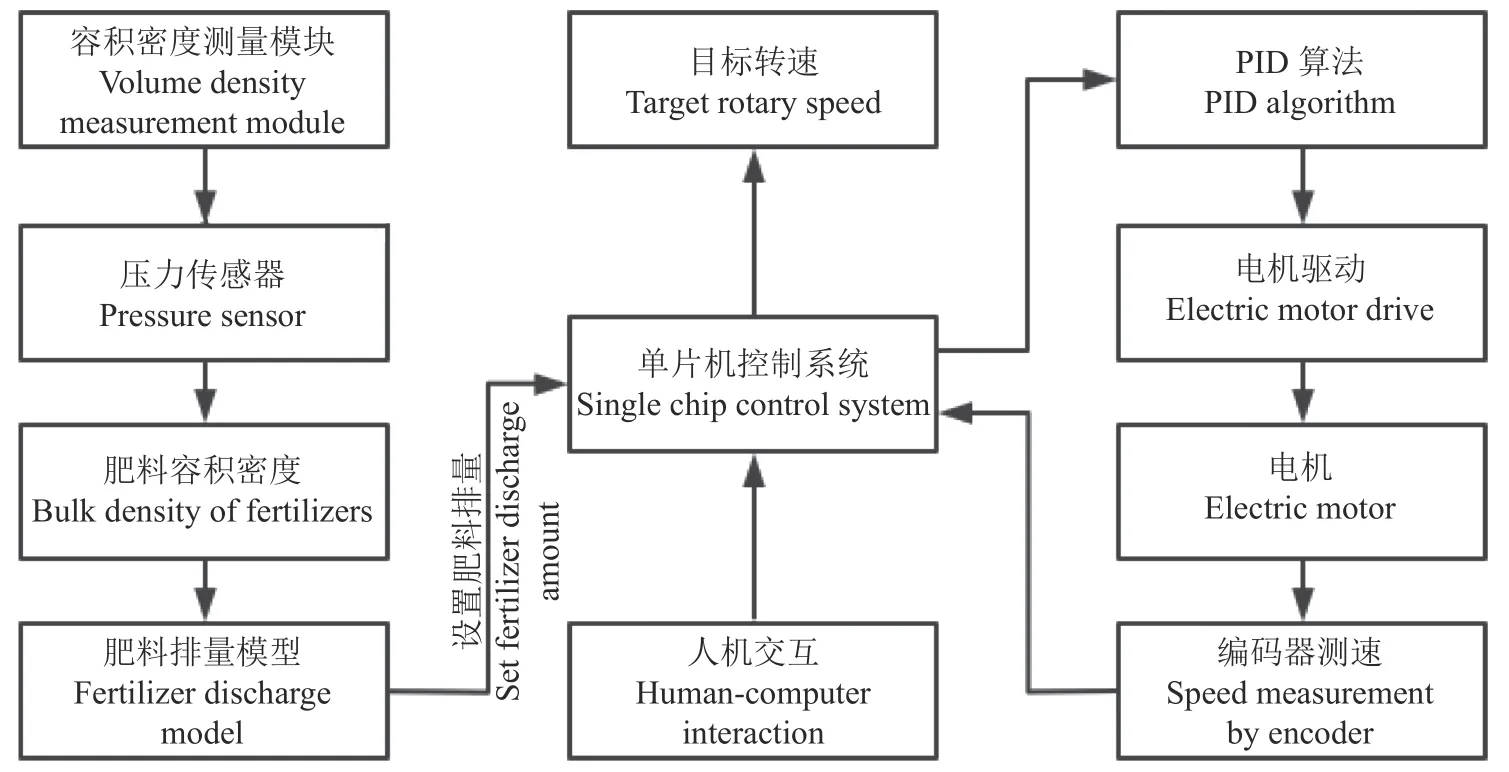
图2 自适应施肥控制系统工作原理框图Fig.2 Block diagram of working principle of adaptive fertilization control system

2 控制系统软、硬件设计

2.1 系统硬件设计

控制系统的硬件主要包括核心控制、容积密度测量、人机交互、地轮测速、电机测速、电源和电机驱动模块。核心控制模块采用宏晶科技生产的STC12CA60S2 单片机，便宜且稳定性高，且内置2 路PWM，适用于电机控制和强干扰场合。控制系统的原理图和印制电路板(Printed circuit board，PCB)由嘉立创EDA 设计完成。人机交互模块采用LCD1602，使用按键和旋钮采集信息。

地轮测速模块和电机测速模块均使用霍尔测速传感器，霍尔测速传感器是常用的转速测量传感器，具有较好测量精度的同时具有较强的抗干扰能力，受温度、灰尘等环境因素影响较小[20]。本系统通过M 法测量转速（v1），公式为：

式中，n为脉冲数；B为编码器分辨率；t1为采样时间，min。

M 法测速的量化误差为1/n[21]，其中，电机通过行星齿轮减速50 倍，再通过链条传动驱动排肥轴。由于系统通过控制电机转速来控制排肥速度，所以将霍尔测速传感器安装在电机轴上(图3)，相比于直接安装在排肥轴上，在使用相同分辨率的编码器时能获得50 倍的脉冲数，其量化误差为直接安装在排肥轴上的1/50，能够提升转速的测量精度，进而提升电机转速的控制精度。

图3 霍尔测速模块安装图Fig.3 Installation photo of Hall speed measuring module

2.2 容积密度测量模块及使用方法

容积密度测量模块(图4) 是通过压力传感器实现的。压力传感器置于1 个具有500 mL 体积的密闭容器下方，系统通过计算得出肥料的容积密度。

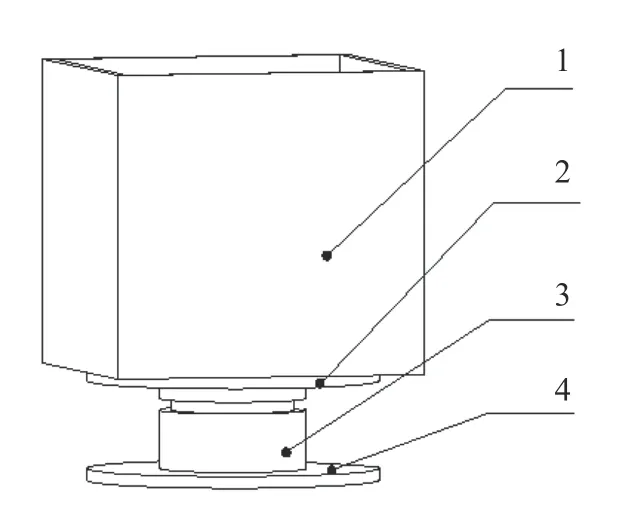
图4 容积密度测量模块Fig.4 Volumetric density measurement module

作业前需将待作业肥料装满整个容积密度测量盒，按下测量按键后，系统将通过公式(5)计算出该肥料的容积密度并保存，测量完成后系统直接读取并保存容积密度，在作业时可以有效避免因震动对测量数据产生的影响。更换肥料种类后，按上述方法再次操作即可。

式中，m为容积密度测量盒内肥料质量，g；V为容积密度测量盒体积，cm3。

2.3 控制系统的软件设计

控制系统模块使用Keil uVision5 编写，主要包括容积密度计算子程序、转速读取子程序、扫描按键子程序、电机转速计算子程序、LED1602 显示子程序以及芯片各外设的初始化。其中，容积密度和电机转速计算子程序是系统设计的关键，直接影响对多种肥料的适应性、排肥速度控制的精确性和稳定性。

设计软件的主要功能是将测得的肥料容积密度代入排量模型计算出每转排肥量，结合机具前进速度与肥料单位面积使用量，计算出电机的对应转速，并将读取到的机具前进速度、电机转速、肥料容积密度和用户输入值显示在屏幕上。

2.4 电机转速的控制

排肥器的动力驱动为一个24V 直流775 的减速电机，本系统使用PID 闭环控制算法来实现电机转速的精准控制。PID 控制算法根据目标值与实际值的偏差，对偏差进行比例、积分、微分运算，得出控制量，根据控制量控制输出，使系统完成自动调节[22-23]。其控制原理如图5 所示。

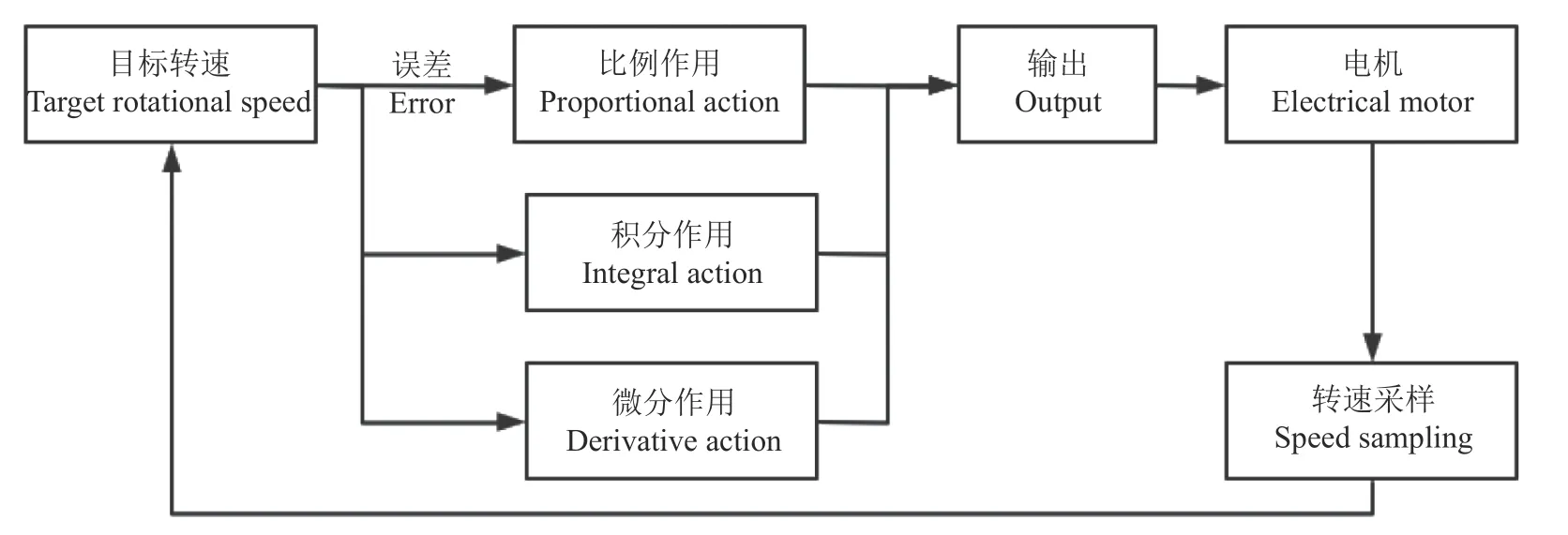
图5 PID 控制原理图Fig.5 PID control schematic diagram

PID 算法的控制公式为：

式中，kp为比例增益，TI为积分时间常数，TD为微分时间常数，u(t)为控制量（控制器输出），e(t)为被控量与给定值的偏差。

若使用位置型PID 算法，计算时需要对e(k)进行累加，增加了计算量，且算法的输出值直接对应执行机构的控制值，在实际控制过程中一旦发生计算错误，会导致执行机构的大幅动作。而增量式PID 公式(7)只与e(k)e(k-1)e(k-2)的3 次测量值相关，适合电机转速的控制[24]。故本研究采用增量式PID 控制电机的转速。

3 材料与评价指标

3.1 试验材料

试验地点为南京农业大学工学院农机库。材料包括自制自适应施肥台架、电子秤、缓混肥(汉枫，0.82 g/cm3)、尿素(东平湖，0.92 g/cm3)、复合肥(史丹利，0.90g/cm3)、过磷酸钙(湖北丰乐，1.31 g/cm3)、氯化钾(中化，1.17 g/cm3)。

自制台架使用的外槽轮排肥器为北禾电子排肥盒，槽轮有效工作长度为6 cm，槽轮直径6 cm，槽数为6。容积密度测量模块使用的压力传感器型号为yzc-133，量程1 kg，综合误差0.05%。

3.2 评价指标

参考国标GB/T 20346.2—2006 及文献[25]设置施肥机在相同排量下不同肥料实际排量的变异系数为评价指标，用以评价使用不同肥料时施肥控制系统实际排量的均匀性，通过此指标对自适应施肥控制系统的适应性进行评价；排肥速率误差为评价指标，用以对控制系统的排肥准确性进行评价。为了确保试验的准确性，每组试验进行3 次重复并取平均值，相关指标的计算公式为：

其中，

式中，Cv表示排量变异系数；SD为排量标准差，g；为排量均值，g；Xi为第i种肥料排量，g；n1表示肥料种类；γ表示排肥速率相对误差，%；m总表示接料桶内肥料总质量，g；t为排肥时间，s；Q为目标排肥速率，g/s。

4 新型标定公式验证试验

新型标定公式的排量受到容积密度与转速影响，故以排肥器的转速、肥料种类(容积密度不同)为试验因素，并以常规标定公式为对照，验证新型标定公式的准确性。

参考农业机械设计手册与文献[12]选取排肥轴的转速为20～80 r/min、增量为10 r/min，共7 个水平，选取广泛使用的尿素、复合肥和新兴的缓混肥为试验对象，开展新型标定公式的验证试验。首先将肥料箱内的残余肥料清除干净，分别添加不同肥料，设置转速和1 min 的排肥时间。试验结果如表1所示。

表1 不同肥料不同转速的1 min 排量Table 1 1 min displacements of different fertilizers at different speeds g

不同肥料拟合结果如图6 所示，使用常规标定公式对数据进行拟合，复合肥、尿素和缓混肥具有不同的拟合曲线，这是由于3 种肥料分别具有不同的容积密度，而常规标定公式将容积密度归为固有属性不做考虑，这就造成使用常规标定公式进行标定的施肥控制系统只能针对1 种肥料准确控制排肥量。更换肥料类型时，无法准确控制其排量。

图6 常规(a)和引入容积密度(b)拟合方式对比Fig.6 Comparison between conventional (a) and imported volumetric density (b) fitting methods

而新型标定公式考虑到容积密度的影响，3 种肥料的排量关系可以拟合为一条直线，拟合模型为公式(12)，其决定系数为0.996。

通过公式(12)可以得到不同转速下肥料排量的计算值，与表1 中实际值对比情况如图7 所示。

图7 新型标定公式预测值与实际值对比Fig.7 Comparison between the predicted value and the actual value of the new calibration formula

通过公式计算得出排量相对误差、平均相对误差，通过模型得到的计算值与现有的试验数据对比(表2)，尿素在7 种转速下的最大排量相对误差为3.12%，平均误差为1.84%；缓混肥在7 种转速下的最大排量相对误差为6.58%，平均相对误差为3.63%；复合肥在7 种转速下的最大排量相对误差为2.23%，平均绝对误差为1.61%。

表2 3 种不同肥料不同转速下实际排量相对误差Table 2 Actual displacement relative error of three different fertilizers at different speeds %

式中，σ为排量相对误差，%；m1为实际排肥质量，g；m2为根据模型公式计算得出的理论排肥质量，g；A为平均相对误差，%。

该模型对于不同肥料、不同转速下的排量计算值与实际值较为接近，能够较好地预测使用不同肥料时的电机轴转速。

5 排肥性能试验与对比试验

5.1 排肥性能试验

对于施肥机而言，根据公式(15)改变施肥的面积用量和机具的前进速度，相当于改变施肥机的排肥速率，故机器的前进速度和单位面积肥料施用量2 个因素可由排肥速率代替，所以选用排肥速率和肥料种类为试验因素。参考文献[26-29]播种施肥机械的作业速度为3～5 km/h，幅宽为2.1～2.2 m，施肥量为200～600 kg/hm2，可计算得出所需排肥速率为2.1～11.0 kg/min。综合考虑本试验选用的排肥器排量，选取排肥速率为2 000～12 000 g/min，增量2 000 g/min。共6 个水平。为了探究控制系统对未标定肥料的适应性，除标定使用的3 种肥料外，增加过磷酸钙以及氯化钾。

式中，Q为排肥量，g/min；q为施用量，kg/km2；v为施肥机前进速度，km/h；b为作业幅宽，m。

试验使用自制的自适应施肥控制系统，分别添加不同的肥料、设置不同的排肥速率以及1 min 的排肥时间。使用电子秤称量接料桶内的肥料质量并记录，取3 次试验数据的平均值。试验结果如图8所示。

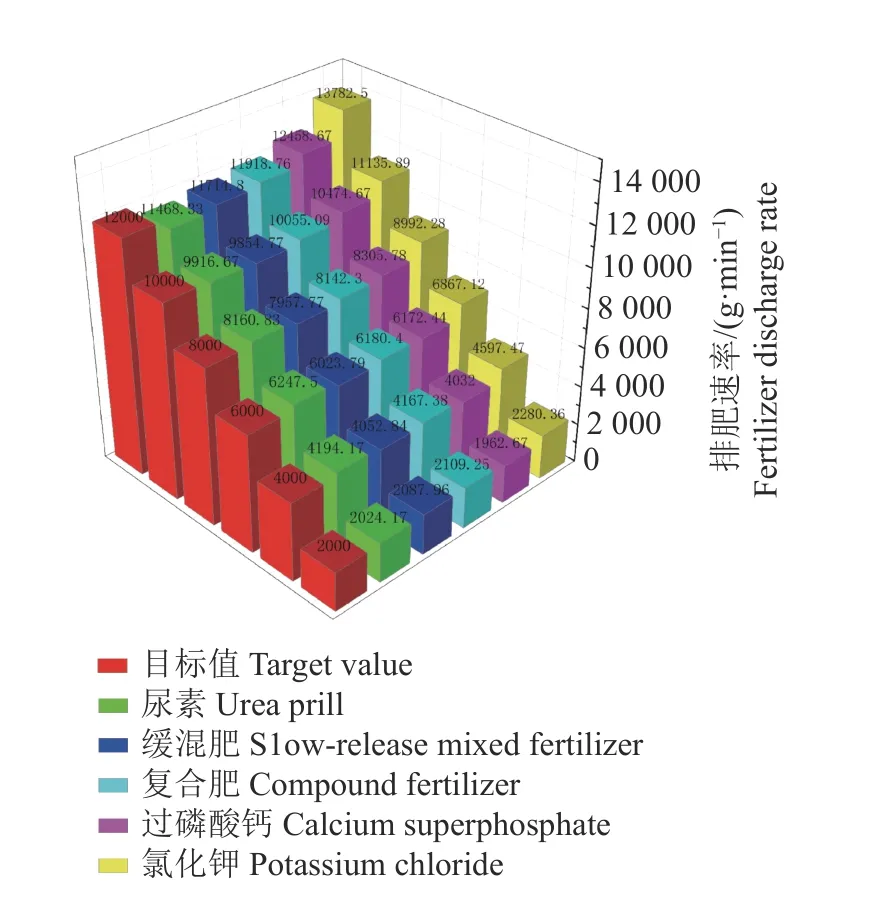
图8 排肥性能试验结果Fig.8 Test results of fertilizer discharge performance

使用球形颗粒肥料尿素、复合肥、缓混肥和过磷酸钙时，如图9a 所示，各排肥速率下排肥误差、相同排肥速率各肥料之间的排量变异系数如表3所示。台架试验表明排量最大变异系数为3.54%，最小为1.53%，均值为2.47%；排肥速率相对误差最大为5.46%，最小为0.40%。其中，尿素相对误差最大为4.85%，最小为0.83%，均值为2.91%；复合肥相对误差最大为5.46%，最小为0.55%，均值为2.62%；缓混肥相对误差最大为4.40%，最小为0.40%，均值为1.75%；过磷酸钙相对误差最大为4.75%，最小为0.80%，均值为2.99%。使用不规则颗粒的氯化钾时，如图9b 所示，排肥速率相对误差最大为14.94%，最小为11.36%，均值为13.67%。

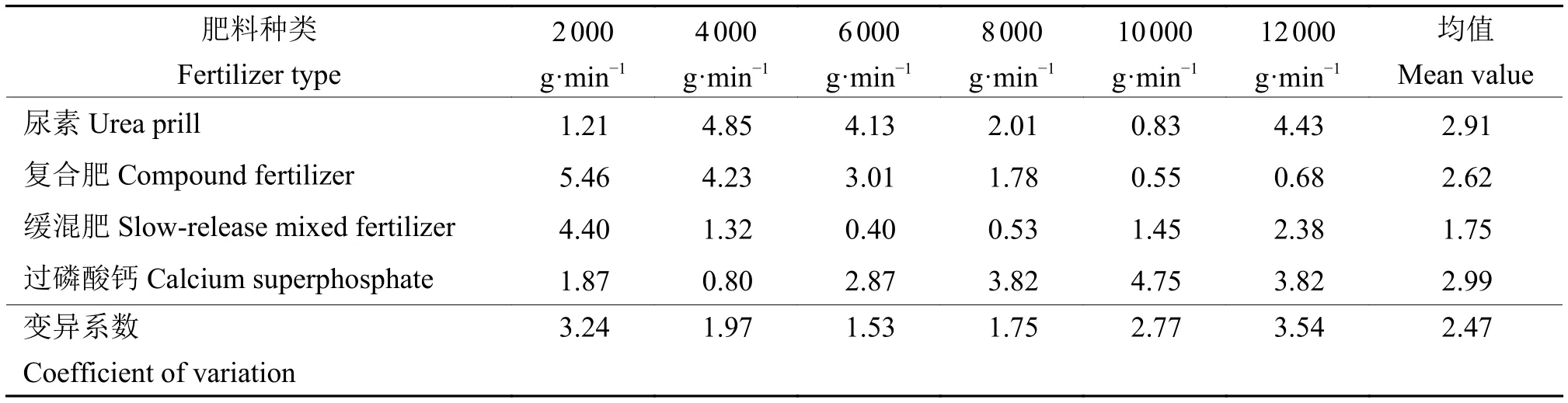
表3 球形颗粒肥料排肥速率相对误差及变异系数Table 3 Relative error and variation coefficient of fertilizer discharge rate of spherical granular fertilizer %

图9 不同类型肥料颗粒对比图Fig.9 Comparison of different fertilizer particles

台架试验表明，本文所设计的自适应施肥控制系统对球形颗粒肥料适应性好、准确率高，提高了常规施肥机械对不同种类肥料的适应性和准确性。为常规施肥机经验式调节或校准的方式提供了一定的参考，对施肥机的进一步智能化具有现实意义，但对无规则的颗粒肥料适应性不足。这可能是因为新型标定公式是依托球形颗粒肥料建立的，而不规则颗粒肥料的填充系数和带动层系数可能与球形颗粒肥料有一定差异，造成不规则颗粒肥料控制精度较差，具体原因还需要深入研究以进一步提升自适应施肥控制系统的普适性。

5.2 与使用常规标定公式控制系统对比试验

常规控制系统使用复合肥进行标定。使用缓混肥、复合肥、过磷酸钙进行和上述试验相同的操作并记录数据，用于和自适应施肥控制系统的排肥情况进行对比。试验结果如图10 所示。

常规排肥模式下的排肥速率误差如表4 所示。分析可知，自适应控制系统使用缓混肥、复合肥、过磷酸钙时实际排肥速率始终接近目标排肥速率，缓混肥最大相对误差为4.40%，复合肥最大相对误差为5.46%，过磷酸钙最大相对误差为4.75%；而使用常规标定公式的控制系统，使用复合肥时排肥速率最大相对误差为4.92%，与自适应模式无明显差异；使用缓混肥时，实际排肥速率明显低于目标排肥速率，最大排肥速率相对误差为10.92%，使用过磷酸钙时，实际排肥速率明显高于目标排肥速率，排肥速率误差在6 种目标排肥速率下相对误差均大于40%，最大相对误差为50.46。

表4 常规控制系统排肥速率误差Table 4 Relative error of fertilizer discharge rate in conventional control system %

这是由于使用常规标定公式时，是使用复合肥(容积密度为0.90 g/cm3)标定的，所以使用复合肥时能保证排肥速率的准确性，在使用容积密度较小的缓混肥(0.82 g/cm3)时，实际排肥速率低于目标，当使用容积密度较大的过磷酸钙(1.31 g/cm3)时，实际排肥速率高于目标。通过对比可以发现，实际作业使用的肥料容积密度与标定所使用的肥料的容积密度相差越大，则实际排肥速率误差越大。而使用新型标定公式时可以将容积密度代入公式，从而保证使用不同肥料时能够精准控制排量。

6 结论

在常规外槽轮排量标定公式的基础上引入容积密度建立新型排量标定公式，解决了常规排量标定公式只适用于单种肥料标定的问题，基于该公式得到了可适用于多种肥料的排量关系模型。该模型的求解数值与实际值最大相对误差为6.58%；平均绝对误差小于3.63%，能够较好地预测使用不同种类肥料时排肥轴所需的转速。自适应施肥控制系统在排肥速率为2 000、4 000、6 000、8 000、10 000、12 000 g/min 时，使用球形颗粒尿素、复合肥、缓混肥、过磷酸钙时，排肥速率相对误差最大分别为4.85%、5.46%、4.40%、4.75%，在不同转速下不同种类肥料的变异系数均小于3.54%；使用颗粒不规则的氯化钾时，排肥速率相对误差最大为14.94%，且相对误差集中在10% ～ 15%。

自适应施肥控制系统与使用常规标定公式的控制系统的对比试验发现，自适应施肥控制系统能够有效解决常规系统的单一适应性问题，验证了其对多种肥料的自适应能力和排肥准确性，不仅对标定时使用的复合肥、尿素和缓混肥有效，还对未标定过的球形颗粒肥料过磷酸钙有效。研究取得了预期效果，为施肥机自动适应多种肥料提供了技术支持，为提高施肥机的适应能力和易用性提供了新方案。但自适应施肥控制系统对不规则颗粒肥料的适应性明显弱于球形颗粒肥料，这可能是由于颗粒的形状对外槽轮排肥器的填充系数和带动层系数的影响造成的，如何提升控制系统的适应性仍需进一步研究。