基于局部特征的南极考察站网络效率评价

成昆凤 刘海燕 庞小平

(1 重庆市勘测院, 重庆 401121;2 南方海洋科学与工程广东省实验室(珠海), 广东 珠海 519000;3 武汉大学中国南极测绘研究中心, 湖北 武汉 430072)

0 引言

南极地区特殊的地缘政治使得科学在南极政治中有着导向和旗帜作用[1]。提升国家南极科学研究水平, 是增强国家南极事务话语权最为重要和有效的手段。南极考察站是国家进行南极考察, 提升南极科学研究水平的根本保障, 直接决定国家科考活动开展的类别和范围, 进而影响国家南极事务话语权, 关乎国家在南极地区的合法权利。

目前, 已有30 余个国家在南极建立了考察站。由于传统的南极考察站选址主要对单个考察站建设位置的适宜性进行分析[2-5], 缺少在整体尺度上对考察站网络的空间范围和考察学科的覆盖性、考察站之间物理连通性和考察学科互补性等进行全面科学、定量的分析, 无法达到考察站网络运行效率最大化。

网络效率指信息在网络中流通的平均难易程度[6], 已有的网络效率评价多关注信息在网络中传播的效率, 并未重点考虑网络局部特征[7-10]。Vragović 等[11]在道路交通网络中以网络效率反映网络小世界特征, 揭示网络全局和局部性能的平衡以提高网络运输效率; Latora 和Marchiori[12]在通讯网络中用网络效率确定网络有效运作的关键节点以提高网络通信效率及安全性。这些研究多是针对无权网或简单加权网等普通网络, 均以最短路径反映节点间的相互关系, 忽略了网络节点自身特征。对于南极考察站网络而言, 考察站本身在南极地区的影响力至关重要。

针对以上问题, 本文提出一种基于局部特征的南极考察站网络效率评价模型。通过基于最小二乘法的层次分析法(Analytic Hierarchy Process,AHP)及优劣解距离法(Technique for Order Preference by Similarity to an Ideal Solution, TOPSIS)评价考察站点及其联系的相对重要性, 以点(考察站)、边(考察站间联系)相对重要性体现网络局部特征; 基于局部特征对常规网络效率模型进行修正, 评价南极考察站网络运行效率, 实验流程图如图1 所示。通过以上模型, 量化评估各国考察站网络效率, 以此反映南极考察站网络运行情况, 并分析其产生差异的原因, 为考察设施网络的建设规划和优化提升提供依据。

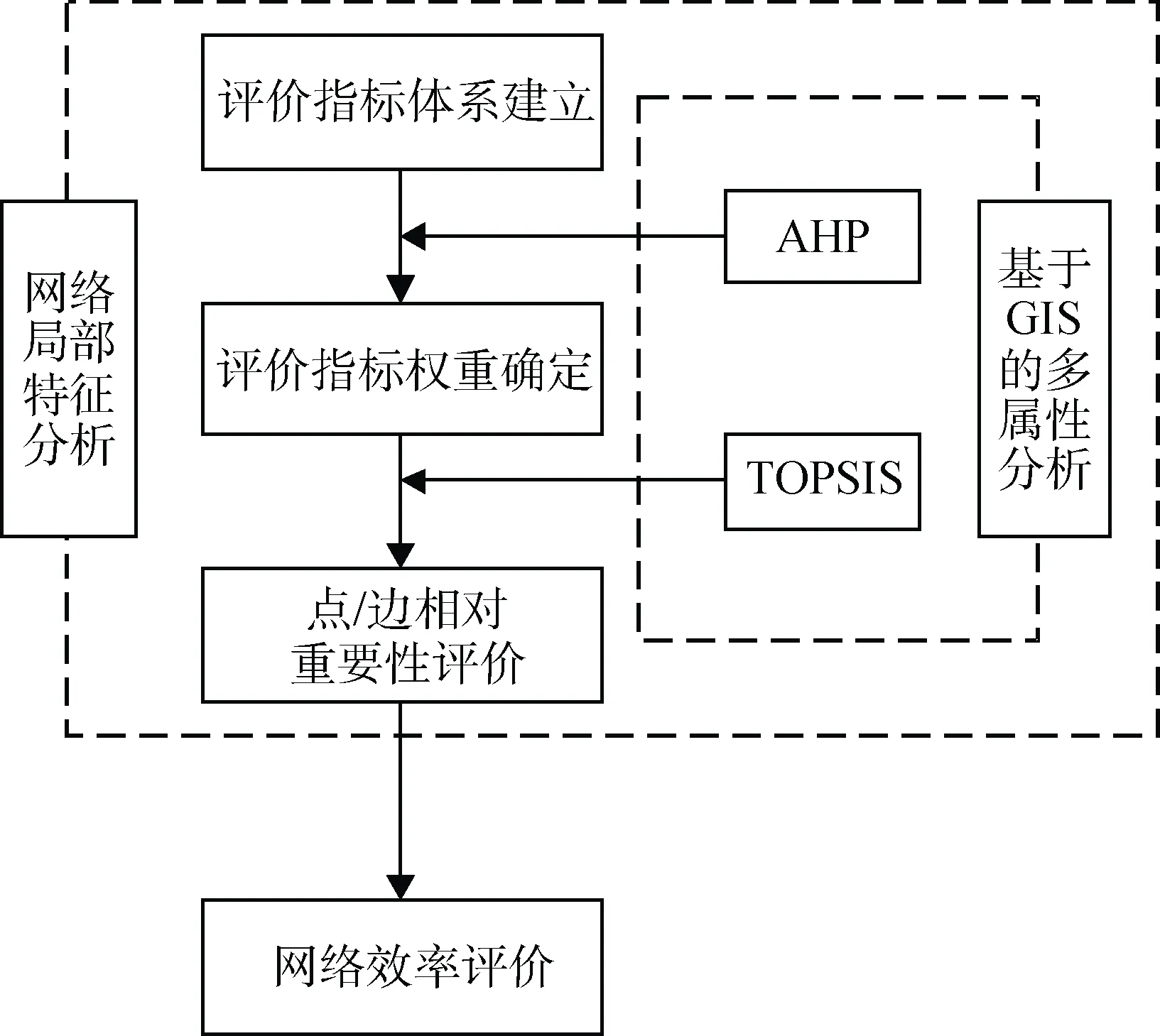
图1 实验基本流程图Fig.1. Schematic diagram of the modeling procedure

1 南极考察站网络效率评价模型

南极考察站网络属于相似权网络, 即单个考察站越重要, 信息在两个考察站间传播效率越高。相似权网络效率(E)[13]评价算法如公式(1)所示:

式中,N为网络中节点个数,为第i个节点和第j个节点之间的最短路径。

由于南极地区特殊的地理位置和环境条件,不同考察站承担不同的功能。考察站之间区位优势、后勤和科考支撑能力之间差异巨大, 造成其实际影响力的差异, 因此在网络效率评价中, 单个考察站的优势(点权重)至关重要。同时, 不同考察站的设立需要考虑补给(如美国麦克默多站和阿蒙森-斯科特站, 中国中山站和昆仑站)、战略区位优势和科考方向的互补性等, 不同考察站之间的互补性(边权重)体现网络的连通性。点权重和边权重共同构筑南极考察站网络的局部特征。

式中,dij为第i个考察站和第j个考察站之间的边权重,vk为考察站点权重。

2 网络局部特征评价

在南极考察站网络中, 点和边的权为相对概念, 故以点相对重要性代替点权重, 以边相对重要性代替边权重。点和边相对重要性均受地理位置、自然环境、地缘政治等多方面因素影响, 故评价点/边相对重要性实际上是一个多属性评价过程。

2.1 评价指标体系建立

2.1.1 点相对重要性评价指标

根据南极地区实际情况, 考虑数据的可获取性,基于相关研究成果[14-17], 从战略意义、后勤支撑能力和科考条件3 个方面建立点相对重要性评价指标体系(表1), 所有二级指标均通过相关性检验。

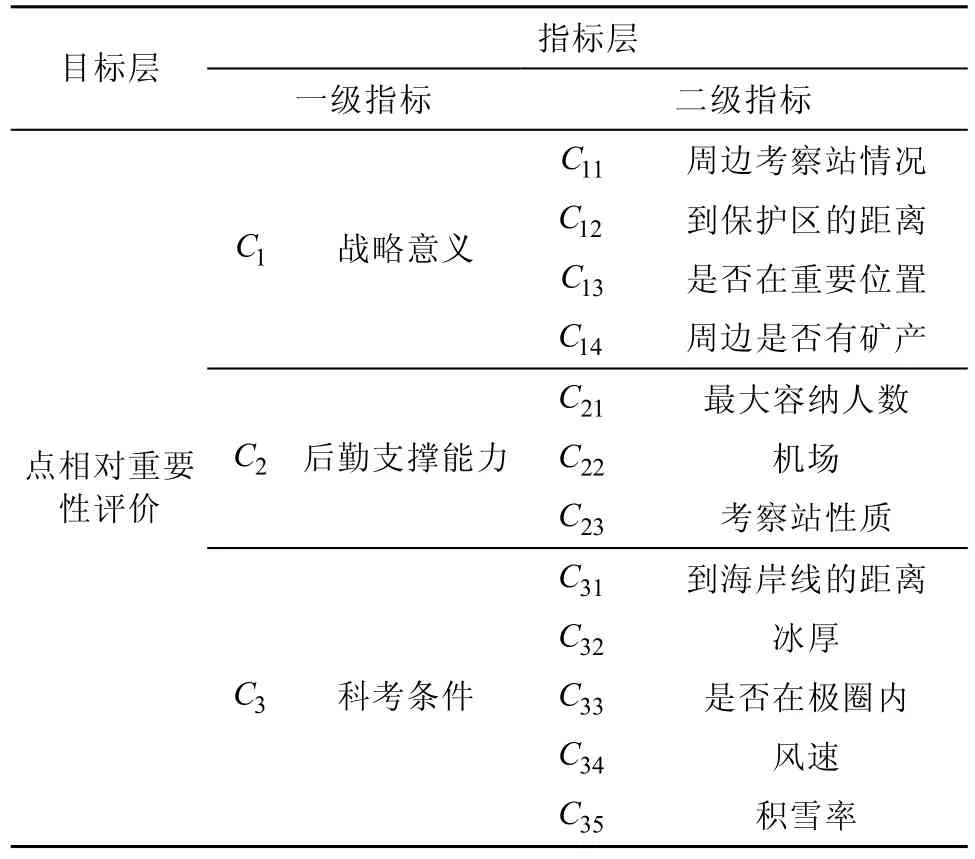
表1 点相对重要性评价指标体系Table 1. Relative importance evaluation index system of points

2.1.2 边相对重要性评价指标

从战略意义、科考条件和后勤支撑能力3 个方面建立边相对重要性评价指标体系(表2), 因指标数量较少, 不进行分级, 分别为是否跨越不同主权声索区、考察站间实地距离、连通方式和研究互补性。

表2 边相对重要性评价指标体系Table 2. Relative importance evaluation index system of edges

2.2 评价指标权重的确定

采用基于最小二乘理论的AHP 来确定指标权重。其基本原理是, 根据完全一致性矩阵H= (hij)n×n的特性(hij为矩阵第i行第j列值,i,j= 1,2,… ,n,wi和wj为排序权向量),在以为约束条件下, 以使有关偏差项小的向量为最终权向量[18]。其εij=wi-hijwj的函数达到最实现步骤分为两步。

1. 构造判断矩阵

采用三角模糊函数构造判断矩阵。专家在对指标进行两两比较时, 往往含有不确定性和模糊性, 模糊判断矩阵能有效反映专家判断时的模糊性特点[19]。

式中n为指标个数,为三角模糊函数, 是指第i个指标相对第j个指标的重要程度,lij、mij、uij为其在坐标轴上的 3 个端点, 且。三角模糊函数的语义偏好范围[20]如表3 所示。

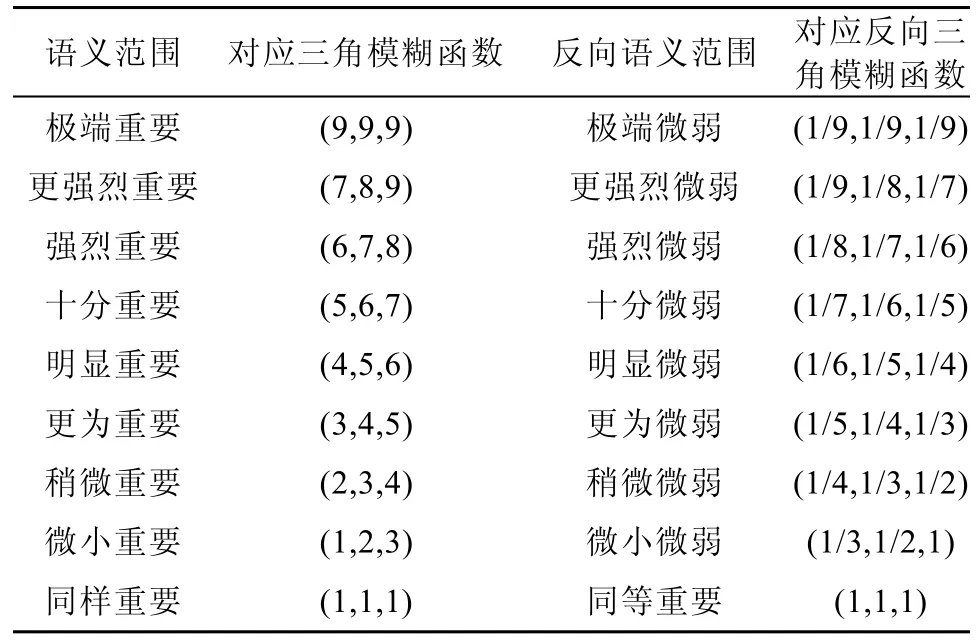
表3 表示各级别偏好语意范围的三角模糊Table 3. Triangular fuzzy numbers corresponding to linguistic scales representing levels of preference

2. 求解权重向量(W*)

解析式W*=B-1e/eTB-1e。其中e=(1,1,L,1)T,。

2.3 点/边相对重要性评价

点/边重要性为相对概念, 本文采用TOPSIS,以每个点/边与理想化目标的接近程度指代其相对重要性。传统多属性评价方法是在对指标进行等级体系划分的基础上对不同方案进行综合评估,但本文中同时存在定性与定量指标, 且点/边相对重要性指标标度差异较大, 等级体系的划分会增加结果的不确定性[22-23]。TOPSIS 的运用可有效避免等级体系划分对结果的影响[24], 其实现过程如下。

1. 点/边相对重要性指标的同趋势化。根据各指标自身特性, 对指标进行同趋势化, 同趋势化方法如下。

式中,yij为同趋势化值,xij为原始数据,xmax为高优指标阈值,xmin为低优指标阈值。

2. 确定最优方案和最劣方案。最优方案Y+为理想状态下, 所有指标均为最理想值的方案,反之, 则为最劣方案Y-。

3. 计算评价方案与最优方案和最劣方案的距离。

4. 计算方案(点/边)排序权iF, 即其相对重要性。

3 模型应用及实验结果

应用上述模型评价中国、美国、澳大利亚三国南极考察站网络效率。由于自动站、暂时关闭站等在南极地区实际影响并不突出, 本文仅评价各国正在运行的常年站和夏季站组成的考察站网络。

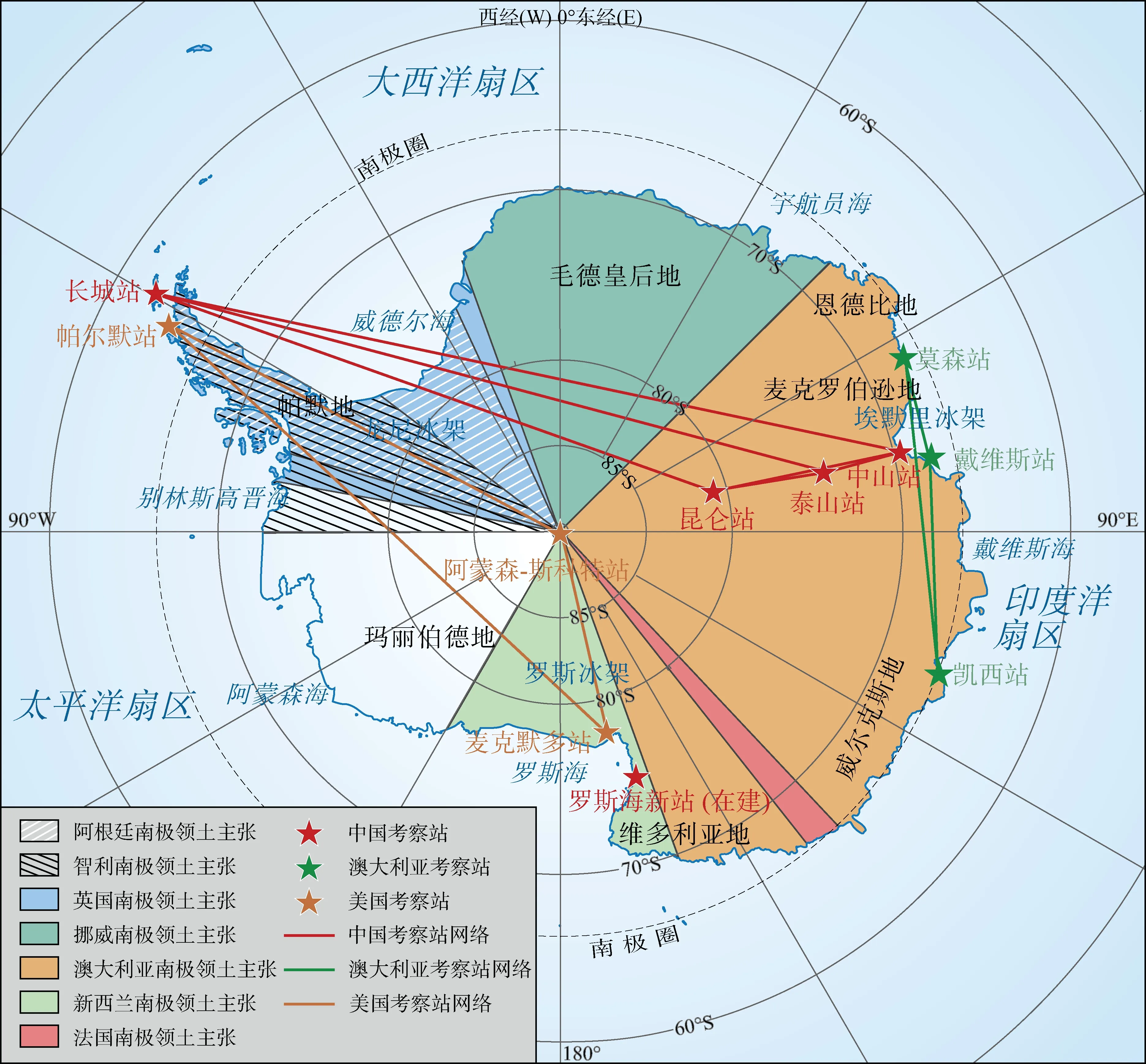
图2 考察站网络示意图Fig.2. Sketch map of the research station network

3.1 数据来源及预处理

为保证数据可靠性, 本文中数据均来自于南极研究科学委员会(SCAR)、英国南极调查局(British Antarctic Survey)等权威机构数据库中最新发布的数据。

在ArcGIS 软件中, 将所有数据做归一化处理, 即所有指标对应数据都在0 到1 之间。具体包括。

1. 定性数据定量化

指标C13、C14、C33均只含有“是”和“否”两种结果, 为便于计算, 将“是”赋值1, “否”赋值0。

南极现存机场跑道类型主要包含海冰跑道、蓝冰跑道、雪橇跑道、压实雪层跑道、砾石跑道等5 类。目前, 南极现存机场有冰雪跑道36 条, 砾石跑道3 条。通常情况下, 蓝冰跑道与压实雪层跑道可起降中/重型轮式飞机; 海冰跑道可满足雪橇式、轮式飞机起降要求; 而雪橇跑道和砾石跑道属于简易跑道。故在C22量化时, 对蓝冰跑道与压实雪层跑道赋值1, 海冰跑道赋值0.75, 雪橇跑道和砾石跑道赋值0.5, 无机场赋值0。

由于南极考察站对周边地区可形成实际考察覆盖, 故不同距离内是否有他国考察站对本国考察站独有的考察覆盖范围具有一定影响, 而同一地区内本国考察站过多也会形成一定的资源浪费,故在对C11进行量化时, 考虑不同缓冲距离内的考察站对站点的影响, 其中[0, 5) km 内无其他考察站为最优, 其他考察站个数大于等于2 时则为最劣; [5,50] km内, 当周边考察站个数为0或1时, 即为最优,当个数大于1 时, 按个数的增加而递减。

本文涉及考察站包含常年站、夏季站, 通常情况下, 常年站影响力更大。对C23进行量化时,常年站赋值1、夏季站赋值0.5。

不同运输方式效率不同, 在南极地区, 空运往往为运输效率最高的运输方式, 其次为船运和陆运。故在对X3进行量化时, 将空运赋值为1, 船运和陆运赋值0.75, 由于资料有限, 某些考察站之间理论上可连通, 但无直接资料证明其连通性,将此类定义为默认连通, 赋值为0.5, 不能直接连通则赋值0.1。

对X4进行量化, 统计各个考察站研究内容,以考察站主要研究方向重叠度进行定量化赋值,赋值区间为0～1。

2. 定量数据标准化

根据南极地区实际情况, 结合相关研究报告以及各类文献数据, 对各类定量数据设置同趋势化阈值。最大容纳人数、冰厚为高优指标, 极少南极考察站可同时容纳200 人以上同时作业; 冰厚越厚可供研究的古气候数据越多, 以3000 m 为冰厚阈值。到保护区、海岸线的距离均为低优指标, 考虑考察人员可到达范围, 设置300 km 为最远距离。

3.2 网络局部特征指标计算

3.2.1 点相对重要性评价指标权重

为提高评价结果客观性和可靠性, 邀请了3位多次参加南极科考的专家对点相对重要性评价指标进行打分, 构造判断矩阵。然后由上述W*的解析式计算各指标权重(表4)。

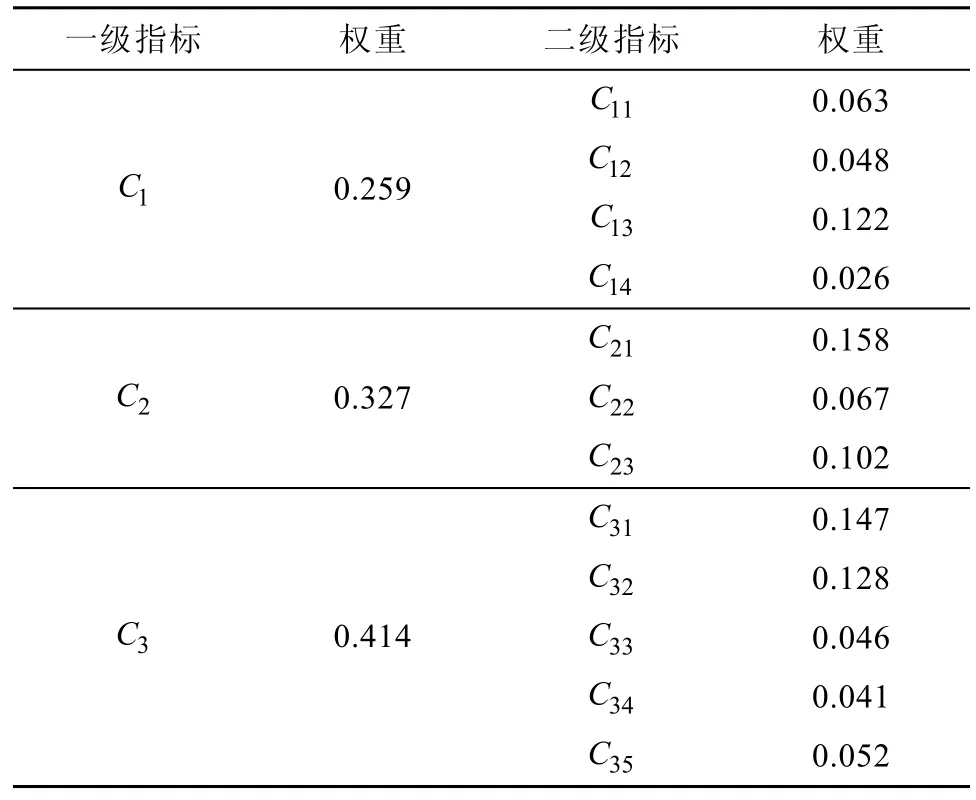
表4 点相对重要性评价指标权重Table 4. Relative importance evaluation index weight of points

从表4 中可以看出, 因目前南极考察站建站主要用途和根本目的是南极科考, 一级指标中科考条件最为重要(WC3=0.414)。其次是后勤支撑能力(WC2=0.327), 南极气候条件恶劣, 后勤支撑是所有极地活动能否顺利进行, 考察站能否健康运行的保障。最后是战略意义(WC1=0.259), 从南极考察站建站历史上看, 各国最初建站目的一定程度上是为在南极地缘政治问题中把握主动权, 目前受《南极条约》约束, 各国只能通过建立考察站增加南极活动, 提升南极科学水平的形式加大在南极地区的实际影响力。

在战略意义二级指标中, 考察站是否在重要位置(WC13=0.122)对考察站的战略意义起决定性作用, 南极最具战略意义的点有极点、冰点、磁点和高点, 占据特殊点有利于国家在南极问题上争取话语权; 其次是周边考察站情况(WC11=0.063),周边考察站分布对考察站进一步拓展建设存在一定限制。

在后勤支撑能力二级指标中, 考察站最大容纳人数(WC21=0.158)反映了考察站规模, 对考察站后勤支撑能力起决定性作用; 其次是考察站性质(WC23=0.102), 决定了该站全年运作时间长短;是否有机场(WC22=0.067)是评价考察站与外界物质交换效率的指标。

在科考条件二级指标中, 由于近年各国对极地海洋研究愈加重视, 到海岸线的距离(WC31=0.147)体现了考察站在极地海洋相关众多学科研究上的便利性, 故该指标权重最大; 冰厚(WC32=0.128)影响冰芯可钻取长度, 冰芯是对南极地区古气候学和古环境研究的重要资料; 积雪率(WC35=0.052)和风速(WC34=0.041)是影响考察站使用年限的重要因素, 也是考察站天气条件的反映。

3.2.2 边相对重要性评价指标权重

采用同样的方法计算出边相对重要性评价指标权重(表5)。从表5中可以看出, 连通方式(WX3=0.389)对边相对重要性起决定性作用, 体现了考察站之间是否连通和两连通站间的运输效率, 涉及考察站之间救援和相互支撑的可能性; 其次体现了是否跨越不同主权声索区(WX1=0.254),影响国家在应对未来可能出现的南极领土纷争时的战略部署; 还体现了研究互补性(WX4=0.248),反映了考察站之间是否存在研究内容冗余, 以及研究领域覆盖情况; 实地距离(WX2=0.109)权重最低, 虽然有利于考察站实地通联, 但不利于多学科研究的展开。

表5 边相对重要性评价指标权重Table 5. Relative importance evaluation index weight of edges

3.2.3 点相对重要性

根据公式5 确定各点到最优方案和最差方案的距离, 然后将表4、表5 中所得权重带入公式6中, 得到点/边相对重要性(表6)。

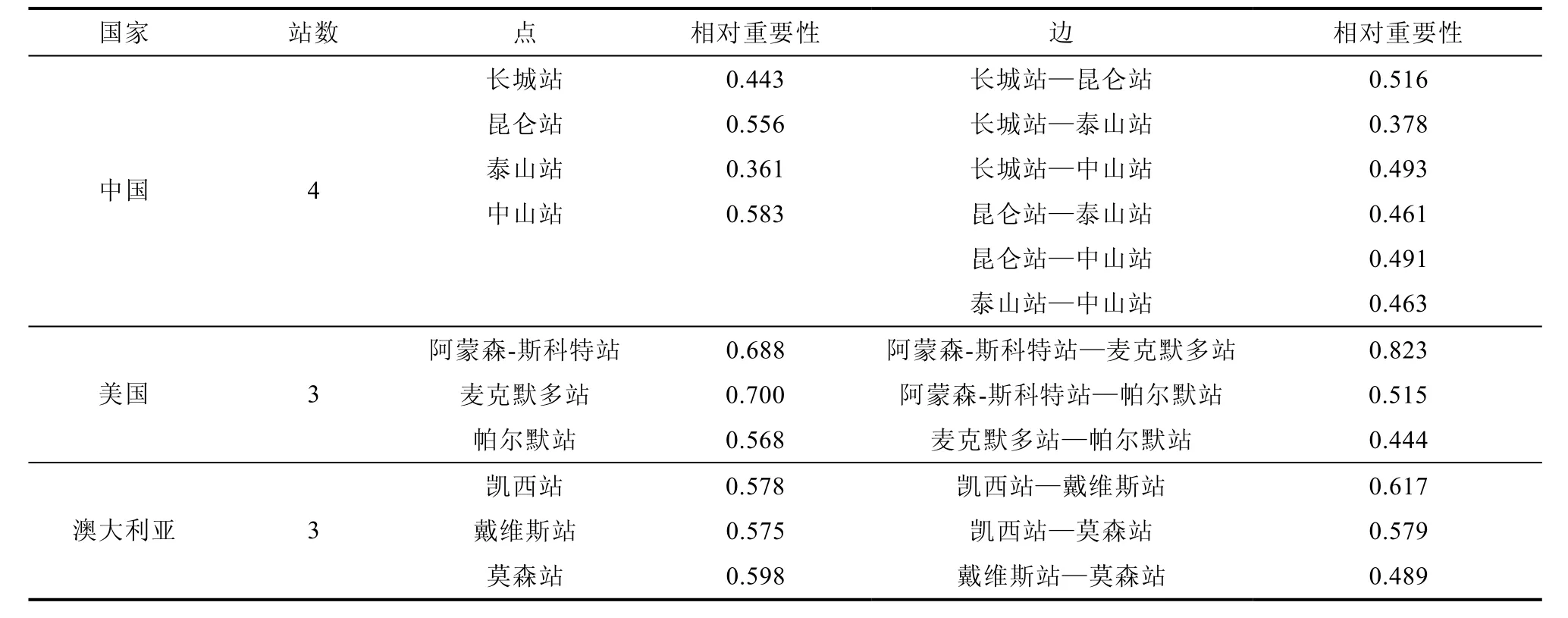
表6 点/边相对重要性Table 6. Relative importance of points and edges

对于点相对重要性, 美国各考察站指向性更加明显, 阿蒙森-斯科特站和麦克默多站尤为突出, 前者位于南极极点, 且规模较大, 配置有机场便于物资运输, 是极地地质学、天文学研究的理想场所; 后者是目前南极规模最大的考察站,也是阿蒙森-斯科特站的后勤补给中心, 地处麦克默多湾罗斯岛, 紧邻罗斯海和罗斯冰架, 利于极地海洋学、极地冰川学研究。澳大利亚考察站的相对重要性则较为一致, 在本研究中, 均处于中等偏上水平。中国考察站中, 中山站相对重要性最高, 作为昆仑站和泰山站的后勤支撑站, 保证其正常运行, 是中国南极科考深入南极内陆的基础, 该站位于普里兹湾沿岸, 紧邻埃默里冰架,是极地冰川学、海洋学研究的理想场所; 泰山站相对重要性最低, 该站为夏季站, 是中山站和昆仑站的中转站。

3.2.4 边相对重要性

边相对重要性如表6 所示, 各国考察站网络内部边相对重要性差异较大。美国网络中的阿蒙森-斯科特站到麦克默多站在所有研究边中最为重要, 后者作为前者的后勤补给站, 通过空中运输进行物资交换, 运输效率高, 彼此联系十分紧密。中、澳两国网络边相对重要性均不如美国显著, 本文所涉及的边中相对重要性最低的是长城站—泰山站, 两站距离较远不能直接连通, 且两站科考互补性较弱。

3.3 考察站选址网络效率评价

将上述得到的网络点/边相对重要性带入南极考察站网络效率评价模型中, 得到各国考察站网络效率如表7 所示。

表7 各国考察站网络效率Table 7. Efficiency of the network in various countries

美国考察站网络效率最高, 其次是澳大利亚,最后为中国。美国考察站网络中只有3 个考察站,但包含全南极规模最大的考察站和最重要的占据特殊点位的考察站之一, 3 个考察站均为常年站,各个考察站之间相对位置和科研关系设置合理,使得美国考察站网络效率明显优于其他两国。澳大利亚考察站网络也由3 个常年站组成, 考察站规模较大, 科研方向上互补性好, 站点之间距离近, 联系紧密。中国考察站网络由4 个站组成, 但是考察站规模较小, 设施不够完备; 泰山站和昆仑站预定科考项目尚未完全展开; 且各站之间联系不够紧密, 考察站间运输效率整体较低, 故整体网络效率较低。

对比美国与澳大利亚两国考察站网络效率,两者考察站网络组成结构类似, 均由3 个常年站组成, 但是澳大利亚考察站均布设于海岸线附近,并未深入南极腹地, 部分科研活动受限, 且其考察站网络未占据特殊点位, 故澳大利亚考察站网络效率低于美国考察站网络效率。说明在布设考察站网络时, 应该合理布设考察站位置, 拓宽南极科考范围。

对比中国与美国和澳大利亚考察站网络效率,中国考察站多于美、澳两国, 但是网络效率却低于两国, 说明并非考察站个数越多, 考察站网络效率越高。

综上所述, 南极考察站网络效率与考察站的个数之间没有必然的正反比关系, 而不同考察站之间相互关系以及考察站的基本情况也能对网络效率产生影响。故增加考察站数量并不一定能提高考察站运行效率, 合理布设考察站分布位置,既保证单个考察站的优越性, 同时调整考察站之间相互关系才是提升考察站网络运行效率、增强国家南极考察实力的关键。

3.4 模型对比

为对比本文修正后的网络效率模型与原始模型之间的差异, 本文根据公式(1)对各国进行了网络效率评价, 评价结果如表8 所示。

表8 修正前各国考察站网络效率Table 8. Efficiency of the network in various countries before correction

对比表7 和表8, 可以看出模型修正前后计算所得的网络效率存在明显差异。以中国为例,修正前后网络效率分别为0.469、0.229, 现假设所有考察站均为常年站, 那么利用公式(1)所计算的网络效率仍为0.469, 而修正后公式(2)所得的值将大于0.229; 假设所有考察站均为夏季站, 公式(1)所计算的网络效率仍然不变, 而公式(2)所得的值将小于0.229。众所周知, 常年站和夏季站在运行时间、设备设施、考察范围等方面都有较大的差距, 显然公式(1)修正前所得出结果的合理性有待商榷。从数据上看, 修正前中、美两国网络效率差别不大, 而澳大利亚网络效率较高为0.726, 与实际情况和专家意见相悖。故本文对网络效率模型的修正使得其更加适用于南极考察站网络效率评价。

4 结语

本文提出了一种基于局部特征的南极考察站网络效率评价方法, 分别评价了中国、美国、澳大利亚的南极考察站网络效率, 取得了可信结果,并对比了3 国考察站网络效率差异的原因, 为未来考察站选址建设和布局优化提供参考。该方法既考虑了节点间的连通性, 又考虑了单个节点的影响力, 适用于南极考察站网络效率评估。但是在局部特征分析中, 计算量随着网络复杂程度增加而呈显著上升的态势。在后续工作中, 将重点研究复杂网络中站点特性归类方法, 减少计算冗余, 为实际选址工作提供全局参考。