一类分数阶复值神经网络的有限时间同步
2024-01-15朱佳庆张国东
朱佳庆,姚 宇,张国东
(中南民族大学 数学与统计学学院,湖北 武汉 430074)
近20 年来,神经网络逐渐成为热门话题,被学者们广泛研究,并运用于诸多不同的领域,例如:图像处理、模式识别、自动控制和联想记忆[1-4]等。
神经网络的应用依赖于它们的动力学行为,其中,“同步”作为一类十分重要的动力学行为,已被学者们深入研究。根据不同的同步时间,同步可以被分为无穷时间同步和有限时间同步。实际应用中,系统总是被期望在一个有限的时间内实现同步。因此,有限时间同步凭借良好的性能成为了神经网络的重要研究课题[5-6]。
分数阶微分不仅有整数阶的性质,还具有优秀的建模能力和广泛的适用性,可应用于工程控制、生物数学和信号加工等[7-9]。分数阶微分可以更精确地描述神经网络的动力学行为。目前人们研究得到很多分数阶神经网络的优秀成果,例如:分数阶模糊神经网络的有限时间镇定[10]、分数阶神经网络的全局同步[11]和带忆阻的分数阶神经网络的同步[12]等。
1971 年Chua[13]首次提出忆阻,2008 年,惠普实验室研究出实际的忆阻器[14]。近年来,忆阻研究成为热门话题,其杰出的非线性特性令它成为模仿人脑突触的最好选择。因此,学者将忆阻融入神经网络中,得到了一类依赖状态切换的神经网络[15]。
由于缺少相关理论支持,复值神经网络的相关动力学问题很少被人们研究。其实,复值神经网络的计算能力和性能均优于实值神经网络,在对称性检测[16]和二进制运算问题[17]等方面实值神经网络的表现均不如复值神经网络。近年来,通过将复值系统分离为实部和虚部系统,复值系统的渐近同步[18]、指数同步[19]和有限时间同步[20]被深入研究。尽管分离法是可行的,但将复值系统分成两个实值系统会大幅增加理论分析复杂性。由于模型的复杂度较高,分离法也很难被实际应用。Feng 等[21]和Zheng等[22]通过引入一种复值符号函数解决了这个问题,即采用非分离的方法就可以研究复值系统动力学问题。
被上述分析所激励,本文的目标是通过非分离的方法研究一类状态依赖切换的分数阶复值神经网络的有限时间同步。本文的主要创新点如下:
1)研究的系统带有分数阶、复值、状态依赖切换项,涵盖仅研究整数阶神经网络系统[5-6]、分数阶实值神经网络系统[8,10-11,15,23]、非依状态切换的复值神经网络系统[21-22],所得结果更具一般性;
2)不同于以往研究[18-20],本文采用非分离的方法直接研究此类复值神经网络的有限时间同步,所得结果更符合复值系统的实际意义。
3)构建了复值杂合控制器,完全消除了文献[8]中的条件限制fl(±Tl)=0,l=1,2,…,n。
1 预备工作
本节将引入一些有限时间同步和分数阶微积分的一些基础知识。另外,本节还阐述了一些文章需要的引理和定义。
定义1f(t)的分数阶积分定义为
可以由引理1 证明而来,证明过程略。
引理3[22]对任意g(t)∈C,以下式子成立:
2 模型描述
本节给出一类分数阶复值忆阻神经网络
其中:0 <α <1;l=1,2,…,n;ξl(t)∈C 代表第l 个神经元在时间t 的状态;al(ξl(t))代表神经元的自抑制率;blj(ξl(t))表示神经元连接忆阻权值。fj:C→C 代表第j 个神经元在时间t 的激活函数;Il∈C 表示外部输入。al(ξl(t))和blj(ξl(t))满足
为了研究系统的同步行为,相应的响应系统定义为
其中:zl(t)=ηl(t)-ξl(t);dl∈C 是线性反馈增益,ω >0,并且满足Re(dl)>0;λ 是幂律反馈增益并且满足λ >0。ρl(t)设计如下:
从而,我们可以得到误差系统为
在文献[15]的基础上,上述误差系统可以转化为
3 主要结果
本节设计一些控制方法实现依状态切换的分数阶复值神经网络的有限时间同步。
定理1基于假设1 和杂合复值控制器(3),在φl≥0 和0 <β <α 条件下,依状态切换的分数阶复值忆阻神经网络能实现有限时间同步。其停滞时间为
证明:构造一个Lyapunov 函数
基于引理2,有
由假设1、引理5 和引理6,可以得到
基于引理3 和引理4,可得到
将式(8)和式(9)带入式(7)中,可以得到
因为φl≥0,可以得到对于t≥0,有
因为0 <β <α,根据式(11)和引理7,对于t≥T,V1(t)=0,其中
因此驱动系统和响应系统在有限时间内达到同步,定理1 得证。
下面,本文基于复值的1-范数给出定理2。
定理2设计一个新的杂合控制器(12)如下:
参数条件与控制器(3)一样。
若满足γl≥0 和0 <ω <α,驱动系统和响应系统在有限时间内可以达到同步,则停滞时间为
4 数值仿真
本节给出一个具体例子来验证理论结果的有效性。
例1 考虑一个二维的分数阶复值忆阻神经网络
另外,fj(ξj(t))(j=1,2)满足假设1,其Lipschitz 常数F21=F22=1,该驱动系统的图分为实部和虚部,初值分别为ξ1(0)=0.6-1.5i,ξ2(0)=-0.9+1.25i。
相应的响应系统为
其中:系统(14)的初值为η1(0)=-1.25+0.45i;η2(0)=1.05 -0.7i,无控制器时的误差系统状态随时间响应如图1 所示。

图1 无控制器时的误差系统状态随时间响应图Fig.1 Time behaviors of state variables for error systems without controller
取ω=0.1,θ=6,d1=1+i,d2=0.96+0.75i,λ=1,计算可得β=0.85,则0 <β <α,φ1=1.5,φ2=1.38,加控制器后的误差系统状态随时间响应如图2 所示。由定理1 可以得到驱动系统(13)和响应系统(14)在有限时间内达到同步,停息时间T=5.456 s,驱动-响应系统的第一个状态和第二个状态达到同步时的响应图分别如图3 和4 所示。

图2 有控制器(3)时的误差系统状态随时间响应图Fig.2 Time behaviors of the state variables for error systems with control(3)
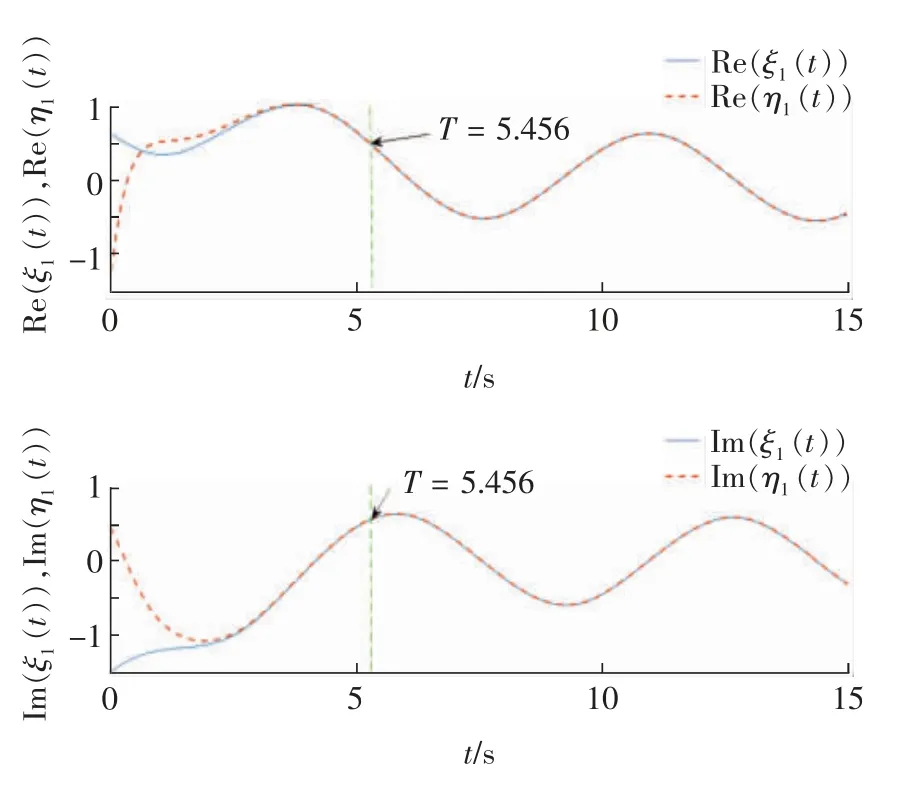
图3 有控制器(3)时的驱动-响应系统第一个状态同步Fig.3 The first state variable of the drive-response systems get synchronization with control(3)

图4 有控制器(3)时的驱动-响应系统第二个状态同步Fig.4 The second state variable of the drive-response systems get synchronization with control(3)
5 结论
本文研究了一类依状态切换的分数阶复值神经网络,通过构建复值杂合控制器和非分离的方法,得到了此类复值神经网络的有限时间同步准则和停制时间的估值。本文所得结果丰富和发展了现有的分数阶复值神经网络的同步控制结果。最后,本文通过数值仿真模拟,验证了所得理论结果的有效性。
在今后的研究工作中,我们将继续考虑带时滞的此类系统,并通过设计相关的杂合控制器来实现其固定时间和预设时间同步控制。
