基于间歇事件触发牵制控制的多智能体系统的有界性
2024-01-15朱润玉
朱润玉,刘 磊
(河海大学 理学院,江苏 南京 213022)
随着信息科学技术的快速发展,多智能体系统已经获得了广泛的关注,其被用于各种领域,包括群集[1]、编队[2]和优化[3]。多智能体系统的稳定性研究被众多科研工作者所青睐[4-8]。
大多数多智能体系统稳定性研究关注的是渐近稳定性。注意到渐近稳定性是在无穷时间区间上的稳定性,但在很多实际系统中,有限时间稳定性比渐近稳定性更实用。文献[9]首次提出了有限时间稳定性,随后,文献[10]扩展到了有限时间有界性。对于带有外部扰动的系统,当初始状态被限制在一个有界范围内,系统状态在固定时间区间上不超过某个阈值,则称该系统是有限时间有界的。在过去的十年里,有限时间有界性被应用于各类系统,包括网络化控制系统[11]、时滞系统[12]和多智能体系统[6]。
在实际系统中,由于一些限制,例如网络攻击和传感器故障,智能体之间也许会通信失败。相应地,学者们提出了间歇控制。间歇控制将时间分割为工作和休息周期,其中休息周期用于故障恢复。间歇控制避免了控制器的连续运行,延长了控制器的使用寿命。最近,曹进德院士及其合作者深入地研究了间歇控制[4,7,13-14]。注意到智能体的数量也许是庞大的,在这种情况下,控制每个智能体是很困难的,自然地,学者们使用了牵制控制[15-20],使得仅对一部分智能体施加控制。
随着数字控制技术的快速发展,事件触发控制被广泛应用于各类系统,包括复杂网络[16-17]和多智能体系统[5,21-22]。在事件触发机制中,预先给定的触发条件决定了控制器的更新时刻,这就减少了控制器的更新次数。
在过去的几十年里,学者们将事件触发控制与其他控制策略整合到一起,形成了一些新颖的混杂控制策略。部分学者研究了基于间歇控制、事件触发控制和牵制控制的混杂控制[16-18],其中,文献[16]中的牵制集合避免了快速切换,文献[17-18]研究了间歇事件触发控制。然而,这3 条文献仅考虑了无穷时间稳定性或者渐近稳定性,并且没有考虑系统受到外部扰动的情况。
受上述文献的启发,本文将利用间歇事件触发牵制控制,研究多智能体系统的有限时间有界性。本文将主要解决以下两个问题:1)设计合适的间歇事件触发牵制控制机制;2)建立多智能体系统的有限时间有界性判据。
1 预备知识和问题描述
在本文中,使用了无向连通通信拓扑G=(V,E)。E={1,2,…,N}表示节点集合;E ⊆V × V 表示边集合。邻接矩阵为A=(aij)N×N,其中aii=0。如果(j,i)∈E,那么aij=aji=1,否则aij=0。拉普拉斯矩阵为L=(lij)N×N。如果i≠j,那么lij=-aij,否则lii=∑jaij。
定义1[20]设条件:1)对于Dt中的任意一个节点i,对i 施加控制;2)对于任意一个不在Dt中的节点j,对j 未施加控制。若上述两条件成立,则称集合Dt为在t 时刻的牵制节点集合。
考虑如下的多智能体系统,i=1,…,N,
其中:f:R+× Rn→Rn;xi(t)∈Rn和wi(t)∈Rn分别是节点i 的状态矢量和外部扰动。设计间歇事件触发牵制控制
其中:k1>0 是控制增益;对任意的i=1,2,…,bi>0;对任意的k=0,1,…,[kT,kT+ρ)是满足ρ≤T的工作区间,[kT+ρ,(k+1)T)是休息区间。系统(1)可被写为
假设1对任意的xi∈Rn,i=1,2,存在一个常数α >0 使得
此外,假设f(t,0)=0。
2 有限时间有界性分析
这就表明对于任意的t∈[kT,kT+ρ),有
对于任意的t∈[kT,kT+ρ),令Lyapunov 函数为
对于t∈[kT+ρ,(k+1)T),令Lyapunov 函数为
接下来需证明对任意的t,
事实上,当t∈[kT,kT+ρ)时,
利用基本不等式和F 的定义,计算可得
利用式(14)和(15)可得
注意到
利用事件触发条件(4)可得
将式(17)和(18)代入式(16)可得
利用条件(6)可得
对于任意的t∈[kT+ρ,(k+1)T),利用条件(7)可得
根据式(20)和(19),式(13)成立。
根据条件(9)和(10)有V1(kT)≤μ2V2((kT)-)和V2((k -1)T+ρ)≤μ1V1(((k -1)T+ρ)-)。当t∈[kT,kT+ρ)时,
多次迭代后可得
当t∈[kT+ρ,(k+1)T)时,
注意到
证明完毕。
注1考虑如下的事件触发机制:
其中φi∈(0,1],信号ζi(t)满足ζi(t)=ζi(0)exp{-γit},ζi(0)>0,γi>0。
由于ζi(t)>0,则相比于事件触发机制(4),事件触发机制(26)减少了触发次数。令则有如下定理。
定理2在条件(6)—(11)和
证明:当t∈[kT,kT+ρ),令Lyapunov 函数为
当t∈[kT+ρ,(k+1)T)时,令Lyapunov 函数为W(t)=W2(t)=V2(t)。
当t∈[kT,kT+ρ)时,类似于定理1,可推导得
其中
由事件触发条件(26)可得
将式(30)和(29)代入式(28)再利用式(27)可得
类似于定理1,可证得系统(3)是关于(c1,c2,,Tf,d)有限时间有界的。证明完毕。
3 数值仿真
下面通过一个数值例子说明本文方法的有效性。考虑一个带有6 个节点的多智能体系统,其通信拓扑满足
其余连接权重都为0。对任意的i,假设bi=1,f(xi(t),t)=0.2xi(t)-0.1sin(xi(t)),扰动满足wi(t)=0.2cos(xi(t)),初始条件满足(x1(0),x2(0),…,x6(0))T=(-2,4,6,-1,1,2)T,Tf=5,T=1。经过简单计算可得α=0.3,d=0.2,c1=62。令R=P1=P2=I。的轨迹和状态变化分别如图1 和图2所示。显然,状态轨迹是发散的。为了使条件(6)—(10)成立,选择参数c2=75。经过计算可得k1≥3.069 8,选择k1=4。牵制节点的变化为{3,2,1}→{3,2,6}→{3,2,1}→…。图3 展示了受控系统在触发机制(4)下的状态变化。选择固定节点集合{1,2,3}和控制增益k1=4,图4展示了受控系统的状态变化。对i=1,…,6,选取γi=3,ζi(0)=1,φi=2,图5 展示了受控系统在触发机制(26)下的状态变化。
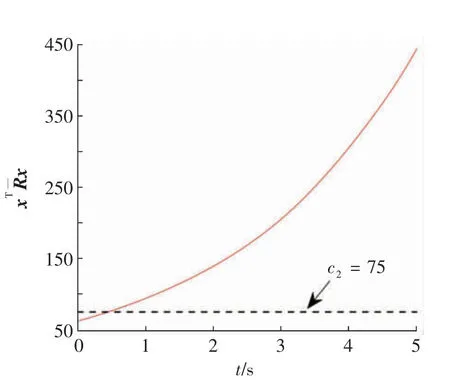
图1 未受控系统的xTx 轨迹Fig.1 The trajectory of xTx for uncontrolled system

图2 未受控系统的状态变化Fig.2 The state of uncontrolled system
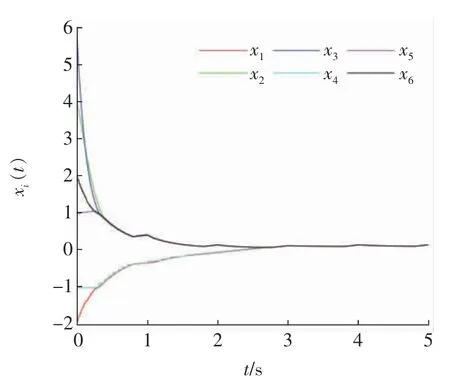
图3 事件触发机制(4)下受控系统的状态变化Fig.3 The state of controlled system under event-triggered mechanism(4)
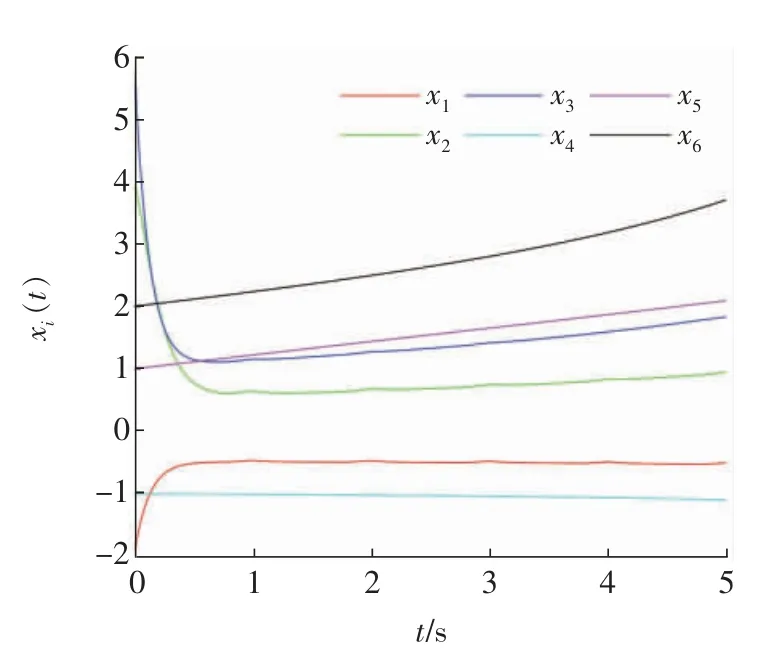
图4 带有固定牵制节点集的受控系统的状态变化Fig.4 The state of controlled system with fixed pinning nodes net

图5 事件触发机制(26)下受控系统的状态变化Fig.5 The state of controlled system under event-triggered mechanism(26)
比较图3 和图4,表明了间歇事件触发牵制控制策略比单一的间歇牵制控制策略更有效。比较图3 和图5,表明了事件触发牵制机制(4)和(26)都可以达到一致性效果。然而,事件触发机制(4)下的触发次数为401,事件触发机制(26)下的触发次数为201,这就说明事件触发机制(26)有效减少了触发次数。
4 结论
本文通过间歇事件触发牵制控制,解决了受扰动的多智能体系统的有限时间有界性问题。首先,设计了两个间歇事件触发牵制控制机制;随后,建立了有限时间有界性判据;最后,通过一个数值例子验证了所提方法的有效性。
