一类耦合非线性薛定谔方程组的求解
2024-01-14仁世杰李永军
仁世杰,李永军,张 娟
(1.兰州城市学院 信息工程学院,甘肃 兰州 730070;2.兰州城市学院 电子工程学院,甘肃 兰州 730070;3.宁夏师范学院 数学与计算机科学学院,宁夏 固原 756000)
0 引言
双芯光纤耦合方程是一类数学与物理领域研究的热点方程,它描述了光纤中光孤子是光波在传播过程中色散效应与非线性压缩效应相平衡的结果.因为光孤立子通信具有高码率、长距离和大容量的优点,可以构成超高速传输系统,所以光孤立子及其在通信中的应用研究具有重要的研究价值. 文献[1]研究了变系数线性耦合的非线性薛定谔方程组:
(1)
其中:βj1(j=1,2)是第j个纤芯的群速度参数;βj2(j=1,2)是第j个纤芯的色散参数;γi(i=1,2)是非线性参数;c是两个纤芯之间的线性耦合参数;δa是两个纤芯的相速度参数.对于方程组(1),文献[1]针对非线性定向耦合器中光学明孤子的相互作用动力学进行了广泛的数值研究,考虑群速度失配,相速度失配,以及群速度色散和有效模面积的差异等因素的影响,主要使用数值方法研究了在均匀白躁声形式下的谐波无穷小扰动作用下亮孤子的稳定性.求解此类方程学有以下方法:IST方法[2-3],齐次平衡法[4-5], Bäcklund变换方法[6-7],Sine-cosine方法[8-9]等.本文研究的是变系数的线性耦合非线性薛定谔方程组,方程组为
(2)
通过Painlevé检验,得到当非线性参数和耦合参数满足:
(3)
时,方程组(2)是Painlevé可积的. 本文在条件(3)基础上,首先利用Sine-cosine方法求解方程组的特殊精确解,然后选取满足方程的特定参数,并给出图像,所涉及的计算均由Maple完成.
1 预备知识
Sine-cosine方法是求解非线性数学物理方程的有效方法,主要用于可积系统的求解.本节简单地介绍Sine-cosine方法. 考虑非线性偏微分方程组
(4)
假设方程组(4)的解具有如下形式:
(5)
将(5)代入方程组(4),得
(6)
分离(6)中实部和虚部,则式(6)等价于虚部为0:式(7),实部为0:式(8).
(7)
(8)
求解(7)可得
(9)
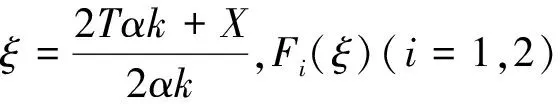
(10)
在方程组(10)中,假设Fi(ξ)(i=1,2)有如下形式:
Fi(ξ)=
Eisin(h(ξ))+Gicos(h(ξ))+Hi(i=1,2),
(11)
其中Ei,Gi和Hi(i=1,2)是待定常数,同时h(ξ)满足常微分方程:

(12)
其中A,B和E是待定常数.再将(11),(12)代入(10)中,整理得到关于sin(h(ξ)),cos(h(ξ))的多项式,令其系数为零,得到关于E1,E2,G1,G2,H1,H2,A,B,E,k和ω的代数方程组.将得到的解带回(12)中,再利用文献[10]中介绍的Sine-Gordon方程(12)的解,可以得到方程组(4)的解.
2 方程组的求解
本节使用Sine-cosine方法和特殊变换求方程组(2)的一组精确解.
定义下列函数:
(13)
方程(2)可经过变换:
(14)
转化为方程(4).故先求解方程(4)得到方程的解U(X,T),V(X,T),然后再通过变换(14)就可以得到原方程组(2)的解.
由第一节求解方程组(4)可以得到E1,E2,G1,G2,H1,H2,A,B,E,k,ω的代数方程组,令
D1=4H1α2k4-4H1αk2ω+
4H2αk2μ+2AEE1-BEG1,
D2=4H2α2k4+4H1αk2μ-
4H2αk2ω+2AEE2-BEG2,
D3=4E2α2k4+4E1αk2μ-
4E2αk2ω+A2E2-ABG2+E2E2,
D4=4G1αk2μ-4G2αk2ω+
2A2G2+3ABE2-B2G2+E2G2,
则代数方程组有如下表示,
-24Ε1G1H1αβk2+3AEG1+3BEE1=0,
(15)
12E12H1αβk2-12G12H1αβk2-
3AEE1+3BEG1=0,
(16)
12E12G1αβk2-4G13αβk2-
2A2G1-4ABE1+2B2G1=0,
(17)
4E13αβk2-12E1G12αβk2-
2A2E1+4ABG1+2B2E1=0,
(18)
-12E12H1αβk2-4H13αβk2+D1=0,
(19)
-4G1αk2ω+4G2αk2μ+2A2G1+
3ABE1-B2G1+E2G1+4=0,
(20)
-24E2G2H2αβk2+3AEG2+3BEE2=0,
(21)
12E22H2αβk2-12G22H2αβk2-
3AEE2+3BEG2=0,
(22)
12E22G2αβk2-4G22αβk2-
2A2G2-4ABE2+2B2G2=0,
(23)
4E23αβk2-12E2G22αβk2-
2A2E2+4ABG2+2B2E2=0,
(24)
-12E22H2αβk2-4H23αβk2+D2=0,
(25)
-4E23αβk2-12E2H22αβk2+D3=0,
(26)
-12E22G2αβk2-12G2H22αβk2+
4G2α2k4+D4=0.
(27)
求解方程组(15)-(27),选取其中一组非平凡解:
(28)
将(28)代入方程(12),得

(29)
求解微分方程(29),得
(30)
取特定例子如下:
取定常数μ=10,β=-1,α=1,B=-1,E2=3,将(30)代入方程组(11),得

(31)


根据(5)和(28)可知U(X,T)=V(X,T).当常数确定后,则
(32)
由此U(X,T),V(X,T)表示为

(33)
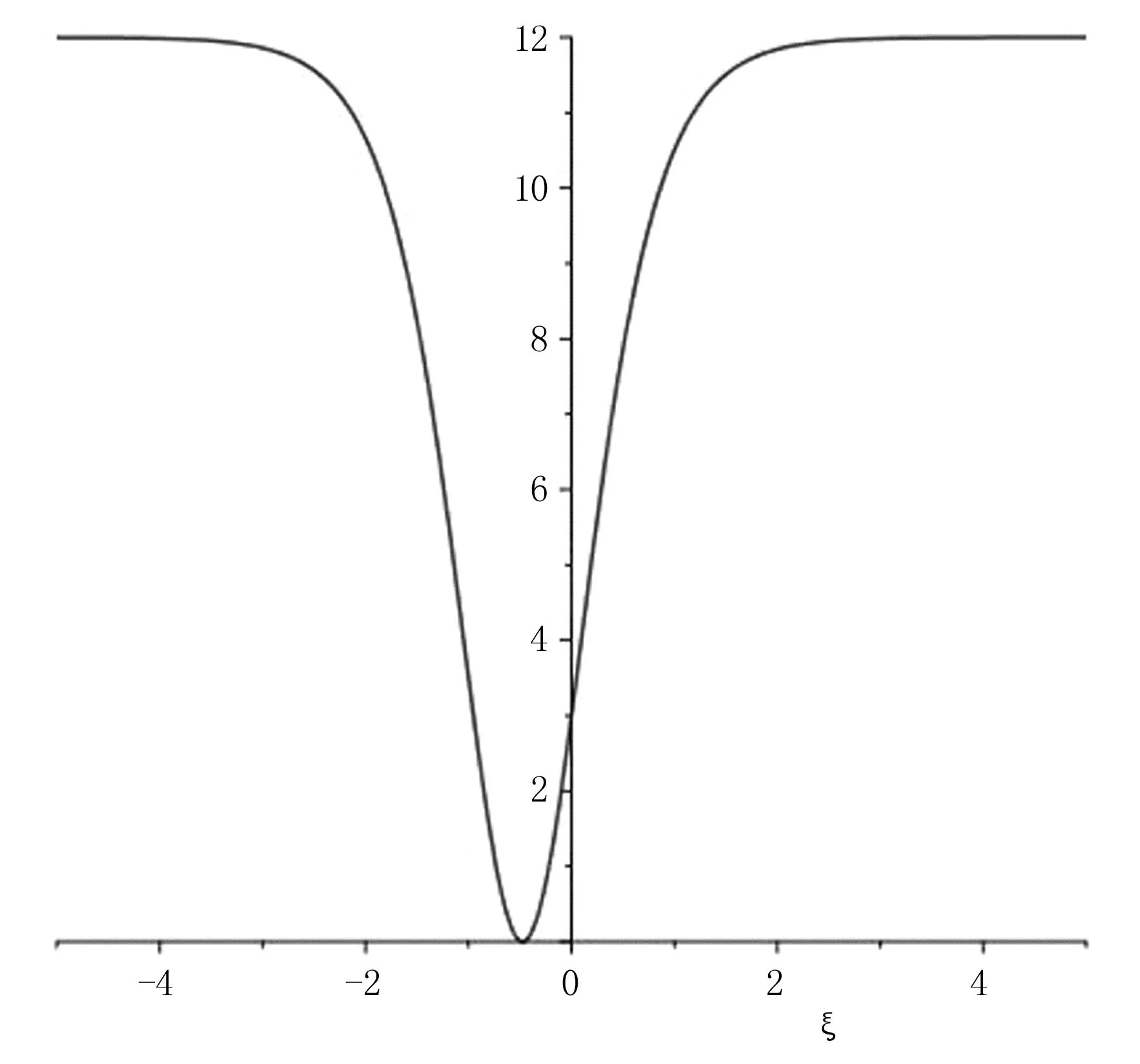
图的图像
限制自变量的范围,得到|U(X,T)|2图像,如图2所示.
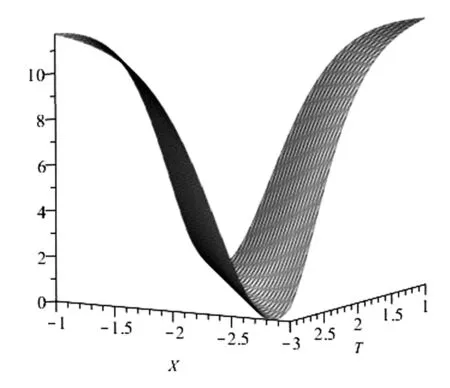
图2 |U(X,T)|2的图像
从图2发现|U(X,T)|2的能量凹陷,即为暗孤立子解.
将(13)代入(33)中,令
u(x,t),v(x,t)表示为

(34)
限制自变量的范围,得到|u(x,t)|2图像如图3所示.

图3 |u(x,t)|2的图像
从图3可以发现|u(x,t)|2的部分能量突起,即为亮孤立子解.
3 结语
本文主要研究的是一类薛定谔方程组在可积条件下,通过特殊变换法和Sine-cosine求解其精确解,然后给定待定的常数,确定方程组精确解的图像.本文的目标方程可进行适当地调整,若将部分常系数改为变量系数,那么可积条件将会发生变化,同时可使用上述方法求方程的精确解.
