基于混合次分数跳过程的亚式期权模糊定价
2024-01-14庞秋月汪育兵
庞秋月,汪育兵
(兰州财经大学 统计与数据科学学院,甘肃 兰州 730020)
期权是重要的金融衍生品之一,期权定价一直是金融工程的重要问题之一.1973年,Black等[1]首次采用几何布朗运动刻画金融资产价格的波动,通过无套利定价方法得到了传统BS期权定价模型.BS期权定价模型无法描述金融市场中的一些现象,如长记忆性,“尖峰厚尾”及“跳跃”等.为了更好地研究金融资产价格变动规律,Mandelbrot[2]和Peters[3]以分形理论为基础将Hurst指数H作为度量长记忆性强度的指标引入到刻画金融资产价格变化的运动中.Necula[4]通过风险中性测度下的鞅方法研究了分数布朗运动下的期权定价问题.余湄等[5]利用鞅定价理论推导出时变混合次分数布朗运动下期权价格的显式解,推广了传统BS和分数布朗运动定价模型.安翔等[6]建立了混合次分数布朗运动下带红利的永久美式回望期权定价模型.

然而,金融市场的不确定性不仅是随机的,而且是模糊的.在真实的金融市场中,数据很难被准确记录,特别是无风险利率、波动率等.Zadeh[13]提出的模糊理论是研究这类模糊问题的重要工具.Wu[14]将模糊理论引入到期权定价研究中.秦学志等[15]研究了分数布朗运动下的欧式期权模糊定价.Liu等[16]运用随机分析、分形理论和模糊理论,构建了次分数布朗运动下的欧式模糊期权定价模型,并分析了Hurst指数对欧式期权定价的影响.
综上,对于亚式期权的大多数研究都是基于分数布朗运动或次分数布朗运动.但这两种随机过程应用在期权定价中会产生套利现象.而研究表明,混合次分数布朗运动在Hurst指数取值为[0.75,1)时,它是一个半鞅,此时,由混合次分数布朗运动驱动的金融市场是完备的且不存在套利机会.目前,已有文献很少同时考虑到金融市场的长记忆性、“跳跃”及模糊等特征.为了更加全面地刻画金融资产的价格变动规律,考虑在模糊状态下用混合次分数跳过程研究亚式期权定价问题.首先在混合次分数跳过程下,运用风险中性原理给出了具有固定敲定价格的几何亚式期权定价公式;其次采用三角模糊数的方法得出模糊定价模型(Fuzzy Geometric Asian Option Pricing,FAOP),给出了股价的模糊区间;最后,数值模拟分析了置信度c和Hurst指数对模糊价格的影响.
1 预备知识
根据执行价格,亚式期权可以分为固定敲定价格期权和浮动敲定价格期权.固定敲定价格的看涨期权和看跌期权在到期日T时刻的收益分别为(AT-K)+和(K-AT)+,其中K是执行价格,AT是标的资产在预定时间内的平均价格.根据AT计算方式的不同,亚式期权又可分为几何平均亚式期权和算数平均亚式期权.几何平均亚式期权中的AT计算公式为
算数平均亚式期权中的AT计算公式为
由于金融资产价格St服从对数正态分布,则容易得到几何平均亚式期权中的AT也满足对数正态分布.但算数平均亚式期权中的AT并不符合对数正态分布,故无法直接得到解析解.学界对算数平均亚式期权问题的处理方式有很多,包括二叉树、近似法及蒙特卡洛模拟方法等.因此,本文只讨论具有固定行权价的几何平均亚式期权.
接下来介绍混合次分数布朗运动和模糊理论的相关概念及性质.

(1)
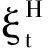
混合次分数布朗运动满足如下性质:

(2)方差:∀t∈R+,
(2)
(3)协方差:∀t∈R+,
(3)
其中,t∧s=min(t,s).
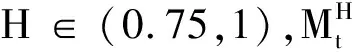


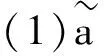
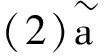



2 资产价格模型及几何亚式期权定价
假设模型满足以下条件:
(1)市场是无摩擦且连续的,即交易费用为零,无税收;
(2)股价遵循Hurst指数为[0.75,1)的混合次分数跳过程,此时无套利;
(3)在期权到期之前,无风险利率r、期望收益率u、股价的波动率σ均为常数;
(4)期权只能在到期日执行;
(5)股票在期权有效期内支付的股息率为零.
在风险中性测度下,股价满足下面的随机微分方程:
dSt=rStdt+σStdXt,
(4)

2.1 混合次分数跳过程公式

(5)

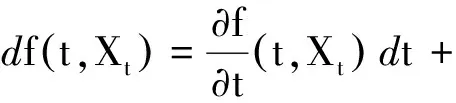
证毕.
定理2方程(4)的解是
(6)
证明令
则有
根据方程(5),有

令St=f(t,Xt),则有dSt=rStdt+σStd(Xt).
证毕.
2.2 几何亚式期权定价模型
定理3在风险中性测度下,股价St满足方程(4),则固定行权价为K、到期日为T的几何亚式看涨期权的价格C(S0,T)为
C(S0,T)=S0eAΦ(d1)-Ke-rTΦ(d2).
(7)
其中
(8)
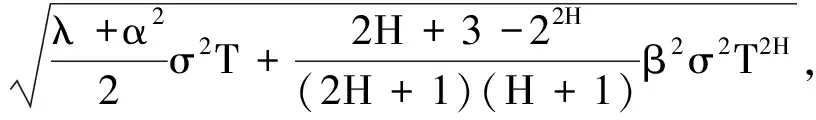
(9)
(10)
证明令
则有
AT=exp{JT}.
其中:
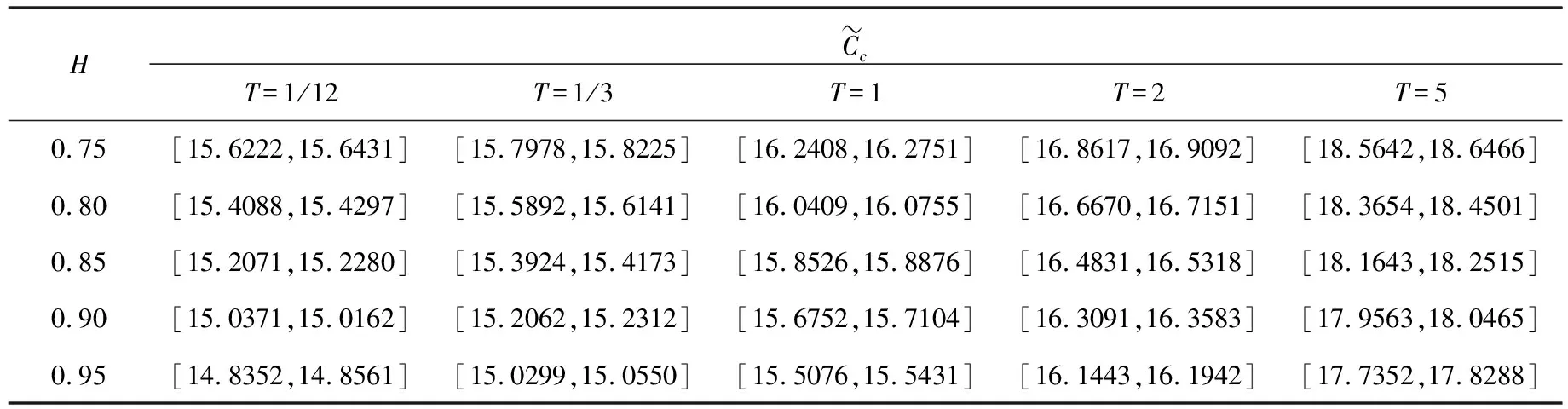
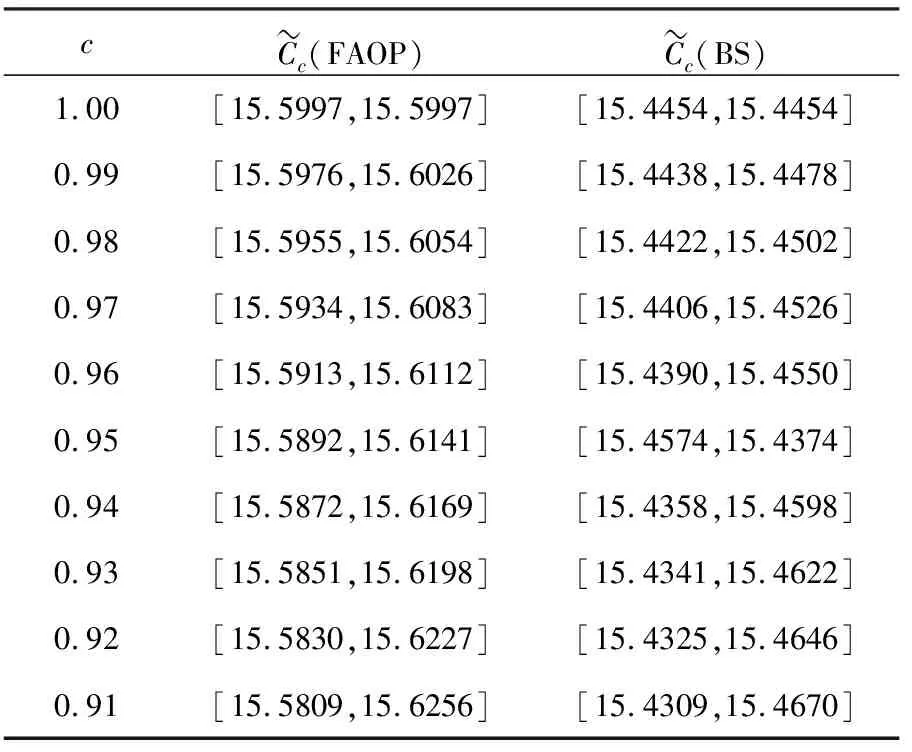
规定s E(XsXt)= 由于随机变量JT=lnAT服从正态分布,因此随机变量AT服从对数正态分布.则几何亚式看涨期权价格为 D={x|ex-K>0}. 这里 其中d1,d2和A分别由式(9)、(8)和(10)定义.证毕. 同理,固定行权价为K,到期日为T的几何亚式看跌期权的价格P(S0,T)为 P(S0,T)= (11) 其中d1,d2和A分别由式(9)、(8)和(10)定义. (12) 其中 (13) (14) (15) (16) (17) 其中 (18) (19) (20) (21) (22) (23) 由式(7)可知, 已知Φ(·)和φ(·)分别为标准正态累积分布函数和密度函数, 则有 Φ(d1)>0,Φ(d2)>0, . S0eAΦ′(d1)-Ke-rTΦ′(d2)>0 , 则有 (1)在不同的置信度c下,几何亚式看涨期权的模糊价格,如表1所列. 表1 不同置信度下的亚式看涨模糊价格 对于c=0.95,表示看涨期权价格处于闭区间[15.5892,15.6141],置信度为0.95.从另一个角度看,如果投资者对信任度0.95感到满意,投资者就可从闭区间[15.5892,15.6141]中获取任何值作为其以后使用的期权价格. 这意味着亚式期权价格的平均水平为15.6135美元,风险为0.009美元. 从表1可以看出,随着置信度c的逐渐增大,模糊价格区间的长度逐渐减小,模糊价格越来越高.换句话说,从可能性均值的角度看,模糊性带来的不确定性提高了亚式期权的价值. (2)当c=0.95时,Hurst指数对看涨期权模糊价格的影响见图1和表2. 图1 T、H对几何亚式看涨期权模糊价格区间左端点的影响 表2 T、H对亚式看涨期权模糊价格区间的影响 由于在混合次分数跳过程下的几何亚式模糊期权价格公式十分复杂,很难准确地判断出关于H的单调性,所以讨论了在不同T下,期权价格关于H的单调性. 表2中分别列举了T取1/12,1/3,1,2和5,5种情况下期权价格关于H的变化.结果发现:从局部上看,控制T不变时,期权价格关于H单调递减;控制H不变时,期权价格关于T单调递增.从图1中可以看出,五条曲线几乎平行.表明在不同的执行时间T下,期权价格关于H的下降速度是相似的. (3)将本文提出的FAOP定价模型与BS模型进行对比,给出不同置信度C下,两种模型的看涨期权模糊定价区间,如表3所列: 表3 不同模型下的几何亚式看涨期权模糊价格区间 从表3中,可以看出FAOP模型得到的模糊价格区间端点值总是比BS模型的大.因为C(S0,T)是关于泊松强度λ的增函数,BS模型中相当于λ=0,所以表3中的结果是合理的. 这意味着亚式期权价格的平均水平为15.4585美元,风险为0.006美元. 从两个模型各自模糊价格的可能下半方差看,BS模型的风险小于FAOP模型.这是因为BS模型中没有考虑到金融市场中股价跳跃所带来的风险. 本文基于混合次分数跳过程模型,运用风险中性原理和模糊理论等,建立了几何亚式期权定价模型及其模糊定价模型.数值实验结果表明: (1)随着置信度的逐渐增大,模糊价格区间的长度逐渐减小,这给了投资者更多的选择机会.对于保守的投资者,虽然可以使用较高的置信度,但可使用的价格范围相对较小,价格相对较高;对于激进的投资者,接受的置信度较低,有更多的价格选择,所以可以用较低的价格来增加收入,但同时也伴随着更大的风险. (2)从局部上看,对于不同的T,期权价格是关于H的减函数,并且期权价格的下降速度大致是相同的;在不同的H下,期权价格是T的增函数,且期权价格的上升速度大致也是相同的. (3)S0、r、σ和λ的不确定性对亚式期权价格的影响是不可忽视的,因此,本文所建立的模糊亚式期权定价模型更加合理.使用此模糊模型,可以帮助投资者选择一个具有可接受置信度的亚式期权价格,以供日后使用.
Cov(Xs,Xt)=Cov(Ms+Qs,Mt+Qt)=
Cov(Ms,Mt)+E(QsQt),
E(QsQt)=E[(Ns-λs)(Nt-λt)]=
E(NsNt)-λ2st=λs(λt+1)-λ2st=λs.

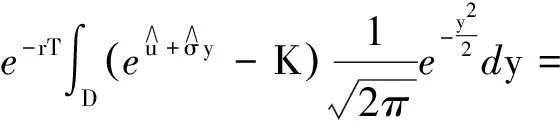
Ke-rTΦ(-d2)-S0eAΦ(-d1),3 几何亚式期权模糊定价模型
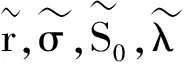





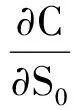

Φ′(d1)=φ(d1)>0,Φ′(d2)=φ(d2)>0


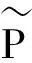

4 数值模拟




5 结论
