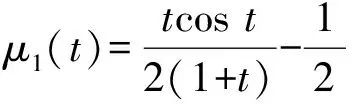G-布朗运动驱动的随机微分方程的全局渐近稳定性
2024-01-13刘存霞
刘存霞
(烟台大学数学与信息科学学院,山东 烟台 264005)
PENG[1-3]建立了有关G-期望,G-布朗运动的基础理论和相应的随机计算,这里G是相应非线性热方程的无穷小生成元。由于在不确定性问题,风险度量以及金融产品定价等方面具有丰富的应用潜力,众多学者对G-期望、G-布朗运动理论开展了大量研究[4-6]。
在系数满足全局 Lipschitz 假设下,PENG[1]首先给出了如下由d维G-布朗运动驱动的n维随机微分方程(G-SDE)解的存在唯一性定理:



(1)
其中:x(0)=x0∈n为初值,B是一个d维G-布朗运动,〈B,B〉=(〈Bi,Bj〉)i,j=1,…,d为B的交互变差,系数f(·,·),hij(·,·),gj(·,·):[0,T]×n→n(特别地,本文中采用 Einstein 记号)。由此,G-布朗运动驱动的随机微分方程解的存在唯一性及相关稳定性问题也迅速成为研究的热点。例如,GAO[7]进一步研究了上述G-SDE解的轨道性质及相应于初值的同胚性问题,文献[8]研究了G-SDE解的指数稳定性问题,文献[9]和[10]分别给出了脉冲G-SDE解的指数稳定性和p-阶矩稳定的充分条件,文献[11]讨论了时滞G-SDE解的渐近有界和 稳定性问题。此外,为克服全局 Lipschitz 假设的局限性,文献[12]通过引入一个Lyapunov 条件,在系数满足局部 Lipschitz 条件的假设下给出了解的全局解的存在唯一性,同时讨论了平凡解的p阶矩指数稳定和渐近稳定等问题。文献[13-14]引入了一致渐近稳定函数 (UASF) 来研究线性时变和时滞系统的稳定性问题,文献[15]基于UASF 改进了若干由有色噪声驱动的非线性系统的稳定性定理。与已有结果来比较,UASF 的引入减弱了构造 Lyapunov 函数时的若干约束。
受以上工作启发,本文研究G-SDE平凡解的稳定性问题,通过 UASF 给出了G-SDE(1)的平凡解拟必然意义下全局渐近稳定的一个充分条件,并通过例子予以验证。
1 预备知识
ρ(ω1,ω2):=
Bt(ω)=ωt为典范过程。
对t∈[0,∞),定义以下记号:
·B(Ω):Ω的 Borelσ-域。
·Ωt={ω.∧t:ω∈Ω},Ft:=B(Ωt)。
·L0(Ω):实值B(Ω)-可测函数空间。
·L0(Ωt):实值B(Ωt)-可测函数空间。
·Bb(Ω):L0(Ω)中的有界元;Bb(Ωt):=Bb(Ω)∩L0(Ωt)。
·Cb(Ω):Bb(Ω)中的连续元;Cb(Ωt):=Cb(Ω)∩L0(Ωt)。
·Cb,lip(d×n):d×n中的有界Lipschitz 函数全体。
·Lip(Ω):={φ(Bt1,…,Btn):n≥1,0≤t1<… ·Lip(Ωt):=Lip(Ω)∩L0(Ωt)。 ξ=φ(Bt1,Bt2-Bt1,…,Btn-Btn-1), 0≤t1 定义 [ξ]:=u1(0,0), 这里u1(0,0)∈且满足对k=n,…,1,uk:=uk(t,x;x1,…,xk-1)是(t,x)的函数且以(x1,…,xk-1)∈d×(k-1)为参数,uk为以下定义于[tk-1,tk)×d上的G-热方程的粘性解: 此时,在G-期望[·]下典范过程(Bt)t≥0是一个G-布朗运动[3]。考虑下述简单过程集: ∀N∈,0=t0<… ξi∈Bb(Ωti),i=0,…,N-1}, ‖η‖p:=[ 其中EP是关于概率测度P的线性期望,B(Ω)是Ω的 Borelσ-域。对于P,相关的容度定义为(A):=supP∈PP(A),A∈B(Ω) 定义1如果(A)=0,则称集A∈B(Ω)为极集。如果一个性质在一个极集之外成立,那么它就被称为拟必然成立(简记为:q.s.)。 引理1(G-Markov不等式)[5]设对任意p>0,X∈L0(Ω)满足[|X|P]<∞,则对任意实数a>0有 ∂xvV(·,X(·))(hvij(·,X(·))+hvji(·,X(·)))+ 下面给出一致渐近稳定函数的定义,详细内容可参见文献[13]或[14]。 首先给出以下定义。 定义4记x(t):=x(t;0,x0)为G-SDE(1)对应初值x(0)=x0∈n的解,若对任意的∈(0,1),均存在函数β∈KL使得 {|x(t)|≤β(|x0|,t)}≥1-,∀t≥0, 则称G-SDE (1)的平凡解是拟必然全局渐近稳定的。 (A1) 系数f(·,·),hij(·,·),gj(·,·):[0,T]×n→n关于变量t均为确定性函数且对任意的x,x′∈B0(R):={a:|a|≤R},存在仅依赖于R的正数CR使得对任意t∈[0,T],均有 |f(t,x)-f(t,x′)|+‖h(t,x)-h(t,x′)‖+ ‖g(t,x)-g(t,x′)‖≤CR|x-x′|, 这里‖·‖表示Hilbert-Schmidt 矩阵范数。 经典的随机微分方程中,局部Lipschitz 条件仅能保证最大区间[0,σ∞)上解的存在唯一性[16],这里 σk=inf{t≥0:|x(t)|≥k}, 且设定infΦ=∞,这一结论在G-SDE中同样成立。为获得局部Lipschitz 条件下G-SDE(1)全局解的存在唯一性,文献[12]给出了以下 Lyapunov-型条件: (A2) 存在 Lyapunov 函数V∈C1,2([0,T]×n;+)以及常数C>0,使得 且对任意的(t,x)∈[0,T]×n,有 LV(t,x)≤CV(t,x), 其中L是如下形式的微分算子: LV=∂tV+∂xvVfv+G((∂xvV·(hvij+ (2) 文献[12]在条件 (A1),(A2) 下证明了G-SDE(1) 全局解的存在唯一性。为研究系统稳定性,引入如下假设: (A3) 对任意的t≥0,f(t,0)=0,h(t,0)=0,g(t,0)=0。 显然,在假设 (A3) 下G-随机系统 (1) 对应初值x0=0存在平凡解x(t)≡0。 定理1对G-SDE(1),设条件 (A1),(A3) 成立且存在函数V(t,x)∈C1,2([0,∞)×n;+),c1,c2∈K∞以及一个UASFμ(t)使得 c1(|x|)≤V(t,x)≤c2(|x|),t≥0, (3) LV(t,x)≤μ(t)V(t,x), (4) 则G-SDE(1) 存在唯一解且其平凡解是拟必然全局渐近稳定的。 应用G-It公式,得 dφ(t,x(t))= (∂tφ(t,x(t))+∂xvφ(t,x(t))fv(t,x(t)))dt+ (∂xvφ(t,x(t))hvij(t,x(t))+ 由引理2,有 φ(t,x(t))-φ(0,x0)= (5) 其中 即 由局部Lipschitz 条件知,G-SDE(1)存在最大解。进一步地,由G-马尔科夫不等式,采用类似文献[12]中 Theorem 3.19 或文献[16]中 Theorem 4.5 的证明方法,易得σ∞=∞,q.s.,即G-SDE(1)存在唯一全局解。进一步地,由条件(4)得 V(t,x(t))≤e-λt+d0V(0,x0)≤e-λt+d0c2(|x0|)。 记β2(t,|x0|)≜e-λt+d0c2(|x0|),由引理1,对0<<1有 {c1(|x(t)|)≥-1β2(t,|x0|)}≤ {V(t,x(t))≥-1β2(t,|x0|)}≤, 从而 -1β2(t,|x0|))}≥1-, 注:由引理3知,当μ(t)=-λ(λ≥0)时是一个USAF,易见定理1的结果在一定程度上推广了文献[12]中的相关结果。 例1 考虑下述G-SDE: (6) 这里B(t)是一个1维G-布朗运动且 Vx(t,x(t))h(t,x(t))=2sin2tx2(t), 及 G(〈Vx(t,x(t)),2h(t,x(t))〉+ 〈Vxx(t,x(t))g(t,x(t)),g(t,x(t))〉)= 从而 LV(t,x(t))=Vt(t,x(t))+Vx(t,x(t))f(t,x(t))+ G(〈Vx(t,x(t)),2h(t,x(t))〉+ 〈Vxx(t,x(t))g(t,x(t)),g(t,x(t))〉)≤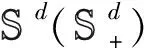




2 主要结果









3 例 子