极限工况下的车辆转向避撞风险指数

黄子文，李莉，周兵，吴晓建，柴天，许艳

(1.湖南大学 汽车车身先进设计制造国家重点实验室，湖南 长沙 410082；2.南昌大学 先进制造学院，江西 南昌 330031)

汽车先进驾驶辅助系统(advanced driver assistance system, ADAS)在汽车主动安全领域发挥了关键作用，典型如汽车主动避撞系统（collision avoidance system, CAS），根据一定的介入准则，在车辆即将发生碰撞时自动介入，减少驾驶员因慌乱产生的操作失误，大大提升了车辆行驶的安全性[1-2].汽车的主动避撞系统一般分为自动紧急制动(autonomous emergency braking, AEB)和自动紧急转向(autonomous emergency steering, AES) 2 种方式，在高速工况，转向避撞方式能以更短的避撞距离避开障碍物[3-4].为了减小高速工况下车辆转向控制的算力负担，Kapania 等[5]提出稳态圆周运动假设下的“前馈-反馈”控制方法，Cui 等[6]在该方法基础上设计了反应式的分阶段避撞系统.来飞等[7]设计了“前馈-反馈”控制跟踪规划的七次项参考路径进行转向避撞.以上研究在计算前馈控制的前轮转角时，没有考虑车辆转向时的横向载荷转移效应，视同一轴的左右侧垂直载荷相等，由于轮胎侧向力和垂向力存在耦合效应，势必影响前馈期望转角的精度.这种情况在大侧向加速度轮胎处于强非线性时更严重.

在转向避撞的过程中，常采用基于规则的决策方法，由评价指标确定不同场景的介入准则.其中转向风险指数（steer threat number, STN）通过车辆避撞所需侧向加速度和最大侧向加速度的比值来描述车辆在路面附着约束下的转向避撞能力，能够较好地反映车辆的侧向加速能力，获得了广泛应用[8].Nilsson 等[9]通过STN 确定了车辆的临界避撞效果，明确了主动避撞系统的工作范围.Hosseini 等[10]在原有STN 的基础上增加车速自适应的预测环节，在不增加预警系统误报率的同时实现了提前预警.Cui 等[6]通过碰撞时间（time to collision, TTC）、制动风险指数（brake threat number, BTN）、STN 的分层逻辑判断，确定了单车道高速场景下制动和转向避撞的不同介入时机.在此基础上，Cui 等[11]通过有限状态机的方式划分邻车道有车场景下的车辆行驶区域，并提出“车-路”耦合威胁评估模型，建立避撞系统在各状态的介入准则和各避撞方式的切换条件.以上对于评价指标的研究进行了车辆点质量模型假设，且通常根据路面附着约束以稳态侧向加速度进行车辆转向避撞能力的评估，忽略了车辆特性对车辆转向能力的影响以及高速转向过程车辆的强非线性和瞬态特性.具体表现为1）车辆在高速大转向的极限工况表现出强烈的非线性，此时车辆具有较大的加速度且轮胎力接近饱和[12]，Pacejka等[13-14]分析了转向过程中轮胎侧偏角变化趋势，认为对于具有不足转向特性的车辆，在纯侧偏稳态转向时，前轮侧偏角大于后轮，因此前轮会先于后轮达到饱和，最终车辆的稳定侧向加速度应由前轮决定，对于具有过多转向特性的车辆则相反[13-14].因此车辆通常难以达到路面附着系数限制的最大稳态加速度.2）在极限工况，车辆表现出高度的瞬态特性[15]，车辆稳态加速度行驶的时间在整个避撞过程中的时间占比较少.本研究提出将侧向位移指数(lateral displacement number,LDN) 作为适用于车辆极限工况的转向风险指数，LDN 的定义为车辆避撞所需侧向位移与最大可达侧向位移的比值，通过阶跃转向实验模拟转向避撞获得最大可达侧向位移，从而反映高速转向过程的非线性并包含转向的瞬态过程.以侧向位移作为避撞条件可以更直接、准确地反映车辆的避撞条件和在极限工况的转向避撞能力.

基于以上分析，本研究1）提出考虑横向载荷转移的转向前馈控制方法以提高控制精度；2）定义最大前轮侧偏角对应的车辆侧向加速度作为该路面上的临界稳定侧向加速度[13-14]，并通过临界稳定工况的角阶跃转向实验得到车辆“纵向位移-纵向车速-最大侧向位移”图，建立LDN；3）在不同附着系数路面、不同侧向避撞距离下采用蒙特卡洛法随机生成10 000 例高速紧急避撞场景，对比LDN、STN 和实际避撞结果，验证LDN 合理性.

1 车辆动力学模型

1.1 非线性二自由度车辆模型

建立如图1 所示包含横摆和侧向自由度并考虑横向载荷转移的非线性二自由度车辆动力学模型：

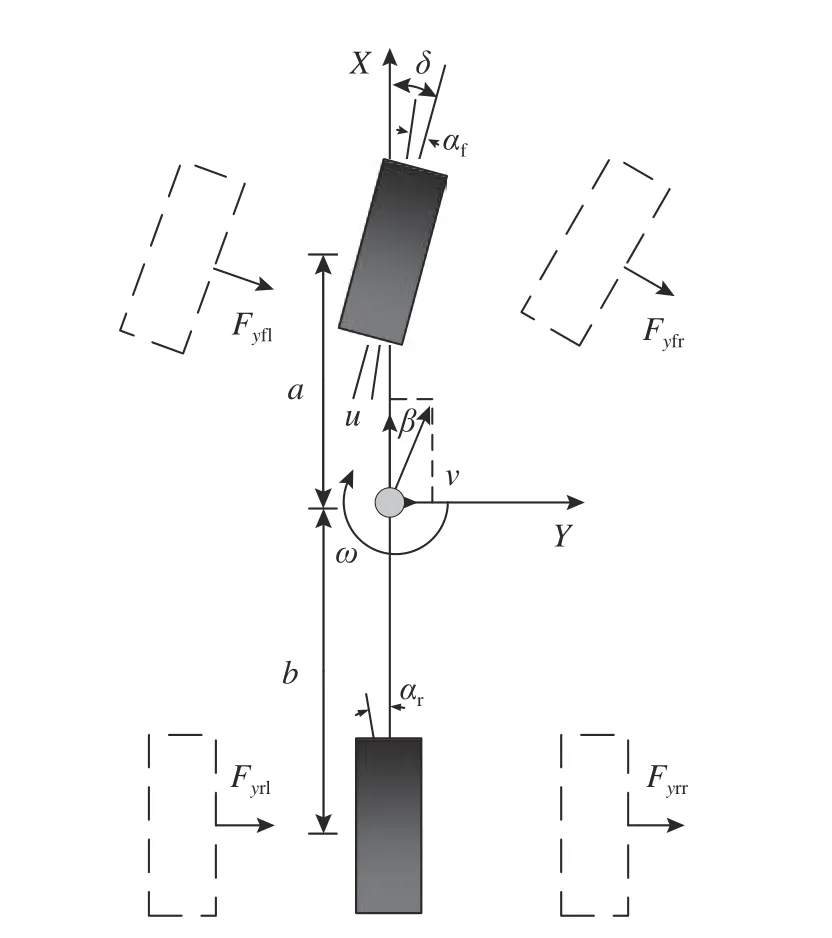
图1 非线性二自由度车辆模型Fig.1 Nonlinear two-degree-of-freedom vehicle model

式中：m为整车质量，u为纵向速度，v为侧向速度， ω 为横摆角速度， δ 为前轮转角，Iz为横摆转动惯量，bs为轮距，a、b分别为车辆质心至前、后轴的距离，Fyfl、Fyfr、Fyrl、Fyrr分别为车辆左前、右前、左后、右后轮胎侧向力.

1.2 轮胎模型

考虑垂向载荷对轮胎侧向力的影响，建立垂向-侧向作用力耦合的非线性魔术公式轮胎模型[13]：

4 个车轮的垂向载荷分别为

式中：ay为侧向加速度，ay=v˙+uω；hs为簧上质量质心高度.

2 考虑横向载荷转移的转向前馈控制

2.1 转向前馈控制

在计算前馈控制的前轮转角时研究者通常采用单轴模型或单轮模型[5-6].单轴模型将车辆前、后轴的静态垂直载荷代入轮胎逆模型，单轮模型则代入单个轮胎的静态垂直载荷.当车辆处在较大的侧向加速度工况时，轮胎的非线性特性明显，车辆的横向载荷转移效应会较大程度地影响前馈转角的准确度，对此本研究提出考虑横向载荷转移的转向前馈控制，分别以4 个车轮的动态垂直载荷代入轮胎逆模型，提高前馈控制精度.

引入横向载荷转移系数：

对文献[5]、[6]中4 个前馈轮胎侧向力修正如下：

其中L为车辆轴距，ay,des为期望侧向加速度，由此可以得到前馈前、后轮侧偏角表达式分别为

2.2 转向前馈控制仿真验证

在不同工况对单轴模型、单轮模型及考虑载荷转移方法进行仿真实验对比.车辆模型参数采用CarSim 软件中C-Class 车型，参数值如表1 所示.进行高、中、低侧向加速度的前轮角阶跃转向仿真实验，分析3 种模型的前馈控制精度.根据式（9）计算得到3 种模型前馈前轮转角进行阶跃转向，结果如图2 所示，其中t为仿真时间.1）低侧向加速度工况：ay,des=0.2g，u=10 m/s.在工况1）中，单轴模型前馈控制转角为4.067°，车辆稳态侧向加速度为 0.223g，稳态误差为 0.023g；单轮模型前馈控制转角为3.496°，车辆稳态侧向加速度为0.200g，稳态误差为0；考虑载荷转移得前馈控制转角为3.506°，车辆稳态侧向加速度为 0.200g，稳态误差为0.可以看出，即使在较小的侧向加速度，单轴模型也存在一定的误差.2）中侧向加速度工况：ay,des=0.5g，u=20 m/s.在工况2）中，单轴模型前馈控制转角为3.987°，车辆稳态侧向加速度为 0.661g，稳态误差为 0.161g；单轮模型前馈控制转角为2.613°，车辆稳态侧向加速度为 0.469g，稳态误差为 0.031g；考虑载荷转移得前馈控制转角为2.768°，车辆稳态侧向加速度为 0.494g，稳态误差为 0.006g.可以看出，中等侧向加速度的单轴模型误差较大.3）高侧向加速度工况：ay,des=0.7g，u=30 m/s.在工况3）中，单轴模型前馈控制转角为4.349°，车辆稳态侧向加速度为 0.819g，稳态误差为 0.119g；单轮模型前馈控制转角为2.118°，车辆稳态侧向加速度为 0.596g，稳态误差为 0.104g；考虑载荷转移得前馈控制转角为2.594°，车辆稳态侧向加速度为 0.674g，稳态误差为 0.026g.可以看出，在较大侧向加速度下，单轴和单轮模型误差均较大.

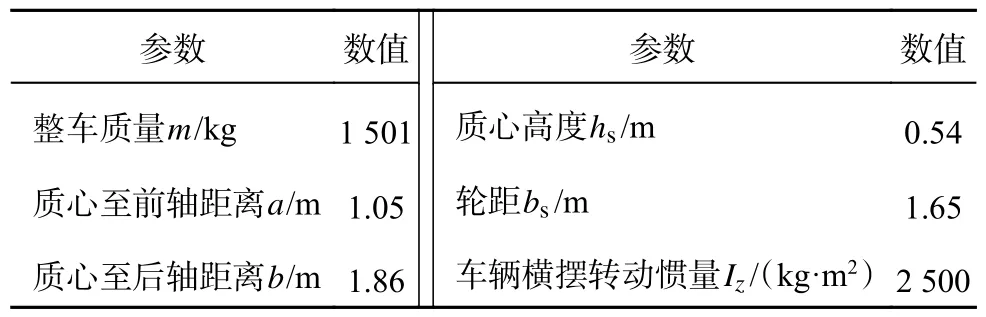
表1 车辆模型参数Tab.1 Vehicle model parameters

图2 不同期望侧向加速度下3 种前馈控制方式对比图Fig.2 Comparison of three feedforward control methods with different desired lateral accelerations

仿真实验结果表明，相比单轴模型和单轮模型，考虑载荷转移在较大侧向加速度的工况前馈控制精度有较大提升.

3 车辆极限工况的转向避撞风险指数

3.1 问题描述

如图3 所示为以恒定侧向加速度进行圆周转向的避撞过程示意.图中，Wh为 本车车宽；Wo为前车车宽；Py为侧向安全距离，Py=0.5Wo+d， 其 中d为考虑传感器误差等增加的侧向安全距离裕度；Px为避撞距离.在较为极端的行驶工况，车辆表现出强瞬态特性[15].如图4 所示，在角阶跃转向输入工况下，从车辆开始转向到车辆侧向加速度达到稳态值的时间为1.1 s；在高速紧急避撞工况下，整个避撞过程的时间通常不超过2 s[16].

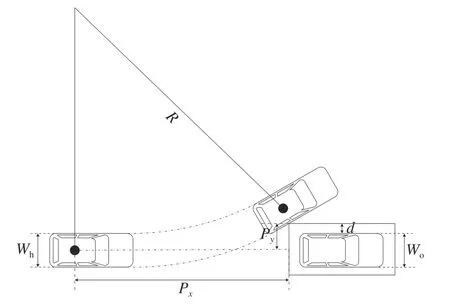
图3 转向避撞示意图Fig.3 Steering collision avoidance diagram

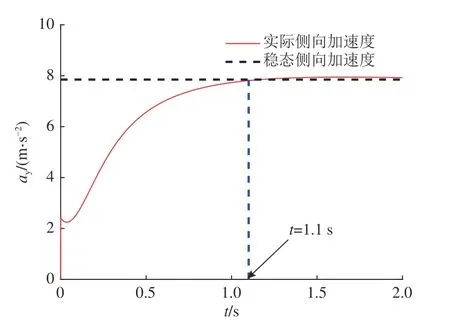
图4 车辆转向过程侧向加速度曲线Fig.4 Lateral acceleration during steering maneuver

本研究提出以车辆最大可达侧向位移描述车辆的转向避撞能力，最大可达侧向位移求解流程如图5 所示.1）分析轮胎侧偏特性曲线和车辆特性，确定车辆的临界稳定侧向加速度，保证车辆在稳定性边界进行阶跃转向；2）在所得侧向加速度下，根据前馈控制算法求得不同纵向速度对应的前轮转角，建立“侧向加速度-纵向速度-前轮转角”MAP 图[17]；3）建立车辆临界稳定的阶跃转向工况，进行仿真实验，得到不同纵向位移、纵向速度下车辆的最大可达侧向位移.

图5 最大可达侧向位移求取流程图Fig.5 Flow chart of maximum steady-state lateral distance

3.2 车辆临界稳定侧向加速度的确定

求解最大可达侧向位移须确定车辆稳定性边界，即车辆行驶的临界稳定侧向加速度.对于具有不足转向特性的车辆，前轮会先于后轮达到饱和，车辆的临界稳定侧向加速度由前轮决定[13-14].本研究以具有转向不足特性的车辆为研究目标，因此对前轮侧偏特性曲线进行分析，如图6 所示.在较大侧向加速度下，轮胎侧偏角既可能在未饱和区也可能在饱和区.为了保证前轮不会进入饱和区，将最大前轮侧偏角对应的车辆侧向加速度作为该路面上的临界稳定侧向加速度[13].当车辆实际侧向加速度小于临界稳定侧向加速度，由于前轮侧偏角不可能在饱和区超出最大值进一步增大，则前轮侧偏角必定在未饱和区，此时车辆能够稳定行驶并保持正常的转向能力.

图6 轮胎侧偏特性曲线Fig.6 Tire lateral deflection characteristic curve

为了获得车辆理论上的最大前轮侧偏角，定义最高车速下的最大前轮转角为极限输入，通过仿真得到极限输入下前轮侧偏角的最大值.普通乘用车最大前轮转角常设计为30°，最高车速为40 m/s，基本能够覆盖所有工况下驾驶员的输入情况.如图7 所示，以 µ=1.0 的路面为例，记录极限输入下前轮侧偏角的变化曲线，其进入稳态后的侧偏角为32.5°±0.1°.结合轮胎侧偏特性曲线可以得到车辆临界稳定侧向加速度（ 0.86g±0.01g）.同理可以得到不同附着系数路面的车辆临界稳定侧向加速度，如图8 所示.

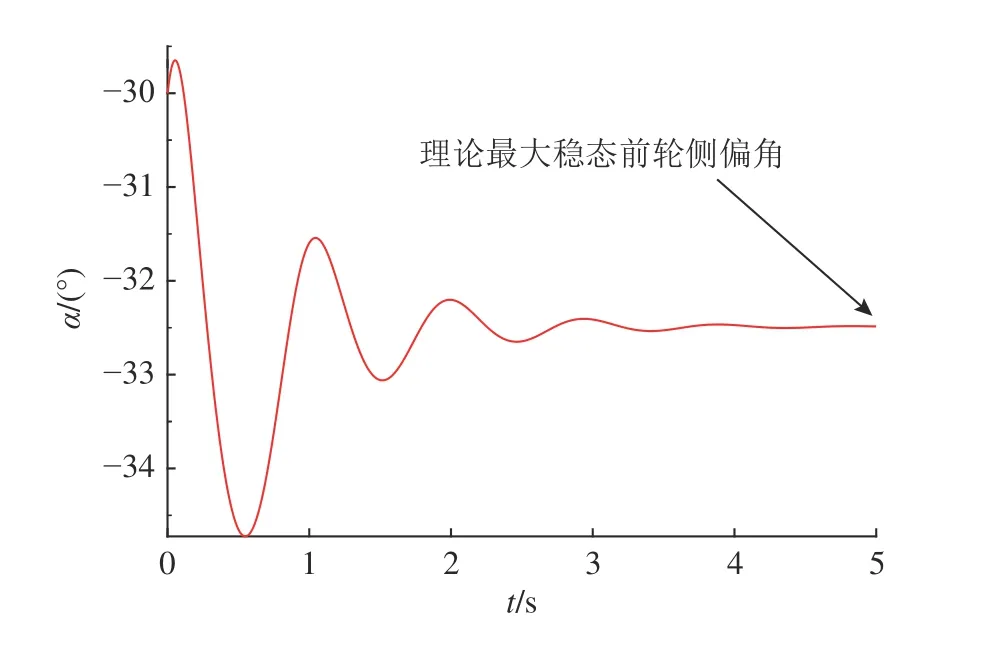
图7 极限输入下前轮侧偏角变化曲线Fig.7 Front wheel lateral deflection angle under extreme input

图8 不同附着系数路面轮胎侧偏特性曲线Fig.8 Lateral deflection characteristics curve of tires on roads with different adhesion coefficients

3.3 “纵向速度-前轮转角”MAP

MAP (maps of achievable performance)[17]用于从全局角度描述车辆的稳态操纵行为.其中“纵向速度-前轮转角”MAP 描述了在稳态圆周运动工况，车辆固定侧向加速度下纵向速度和前轮转角的对应关系.MAP 涵盖车辆所有输入的优点，通过本研究提出的轮胎模型和转向前馈控制方法，求得在临界稳定侧向加速度的“u-δ ”MAP，得到如图9 所示的“侧向加速度-纵向速度-前轮转角”MAP，建立车辆所有稳定性边界的阶跃转向工况.

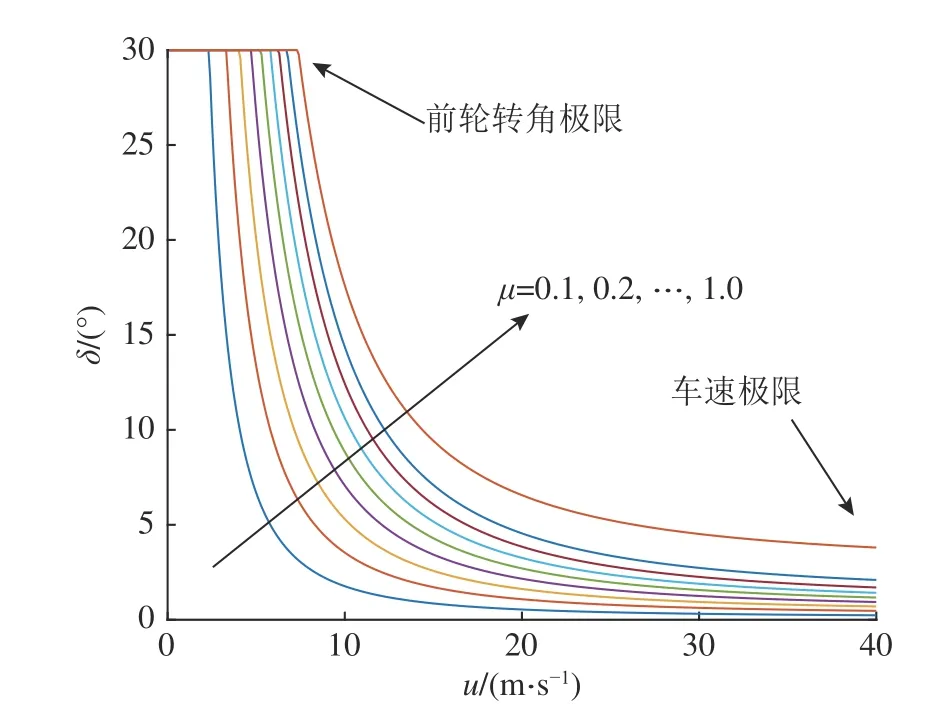
图9 “侧向加速度-纵向速度-前轮转角”MAPFig.9 MAP of “lateral acceleration-longitudinal velocity-front wheel angle”

3.4 最大侧向位移的确定

由“ay-u-δ ”MAP 可以得到临界稳 定工况的车辆纵向速度和前轮转角输入，采用非线性二自由度模型进行前轮阶跃转向仿真实验，可以进一步求得车辆在固定纵向位移的最大侧向位移.如图10 所示为3 种典型附着系数路面下车辆最大侧向位移图.图中，x为纵向位移，ymax为已知避撞距离和纵向速度下车辆的最大侧向位移.

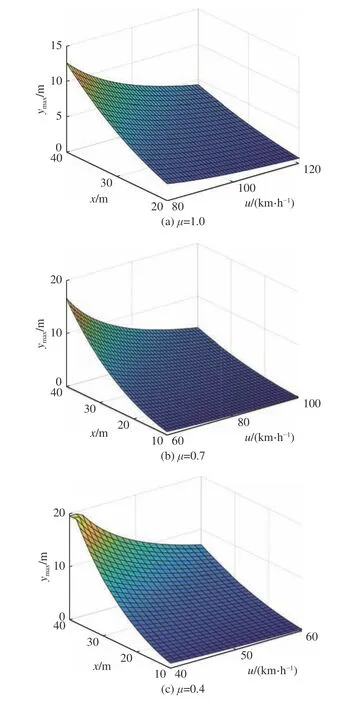
图10 不同附着系数路面的车辆最大侧向位移图Fig.10 Plots of maximum lateral displacement under different adhesion coefficient

3.5 风险指数定义

对于如图3 所示的转向避撞过程，通常认为当车辆纵向位移达到避撞距离Px时，其侧向位移大于避撞所需侧向位移yreq，车辆避撞成功，因此将LDN 定义为车辆避撞所需侧向位移与车辆最大可达侧向位移的比值，由此判断车辆能否通过转向完成避撞，

其中yreq=Py+0.5Wh.实际应用中本车与前车相对位置、速度等状态量由车辆感知模块提供，ymax由图10 可得.对于前车非静止的避撞场景，LDN 可以通过式(10)推导得出：情况1）前车只存在纵向速度和加速度，此时前车在侧向为静止状态，yreq=Py+0.5Wh；假设本车纵向速度不变，根据两车相对纵向速度和加速度预测可得两车纵向相对位移为0 时本车实际纵向位移，已知纵向位移和纵向速度由图10 可以得到ymax.情况2）前车同时存在纵向、侧向速度和加速度，ymax根据情况1）中所述方式得到；根据前车的侧向速度和加速度预测可得两车纵向相对位移为0 时前车侧向位移yo， 则避撞所需侧 向位移为yreq=Py+ 0.5Wh+yo.

4 基于蒙特卡洛法的风险指数验证

蒙特卡洛法通过随机抽样构建概率模型，可以模拟随机现象，适用于解决复杂系统的高维、时间延续性问题[18].Feng 等[19]将变道过程中两车相对位移、相对速度和碰撞时间作为参数建立数学模型，通过蒙特卡洛模拟随机生成测试场景，建立无人车辆的变道行为测试库.受其启发，本研究将路面附着系数、避撞距离、纵向车速作为参数，随机分布生成测试场景，分别用STN、LDN进行判断，通过转向避撞仿真测试进行风险指数的准确性对比， 准确率定义为判断正确的样例数与总样例数的比值.

在如图3 所示的转向避撞场景中，定义STN 为避撞所需侧向加速度和最大侧向加速度的比值[6,10]：

假设车辆在避撞过程做稳态圆周运动，根据如图3所示的几何关系有

取Wh=Wo=2 m ，d=0.2 m ，则yreq=2.2 m ，避 撞 距离Px及 纵向速度u通过随机分布生成.采用团队已有避撞控制研究成果（见文献[6]），将避撞过程分为2 个阶段，阶段1）采用恒定侧向加速度的“前馈-反馈”控制做稳态圆周运动，离开碰撞危险域后，阶段2）采用MPC 控制车身回正并跟踪邻车道中心线.取高、中、低3 种路面附着系数，分别为 µ=1.0 、0.7 和 0.4.在Simulink-Carsim 联合仿真环境下进行相应测试验证.

4.1 高附着系数( µ=1.0 ) 路面极限工况的风险指数准确性验证

针对极限工况，选取的避撞场景主要为较高车速和较短避撞距离.如图11 所示，随机分布生成10 000 例测试场景，取纵向速度为[80, 120] km/h，避撞距离为[10, 40] m，基本覆盖极限的避撞工况，其中nra为随机数列的数量.

图11 高附着系数路面测试场景的参数随机分布Fig.11 Random distribution of parameters for high adhesion coefficient test scenario

STN 通过式（11）判断， S TN<1.0 表示该场景下可以避撞，否则无法避撞；LDN 通过式（10）判断， L DN<1.0 表示该场景下可以避撞，否则无法避撞.对于实际避撞，认为车辆纵向位移在达到避撞距离Px后，其侧向位移大于避撞所需侧向位移yreq，且车辆能正常跟踪邻车道中心线，车辆避撞成功，否则避撞失败.2 种风险指数的预测结果与实际避撞结果的对比以混淆矩阵的形式展现，如图12 所示.图中，ncb为混淆矩阵中各色块的数量.STN 由于忽略车辆特性对转向能力的影响以及高速转向过程中的瞬态特性，其预测值通常夸大了车辆的转向能力.LDN 在稳定性边界得到车辆最大可达侧向位移，但车辆超出稳定性边界一定范围或较短时间内不一定完全失稳，因此其预测值可能低估了车辆的转向能力.总体来说，LDN 准确率为94.96%，STN 准确率为84.31%，LDN 准确性相较STN 有明显提高.

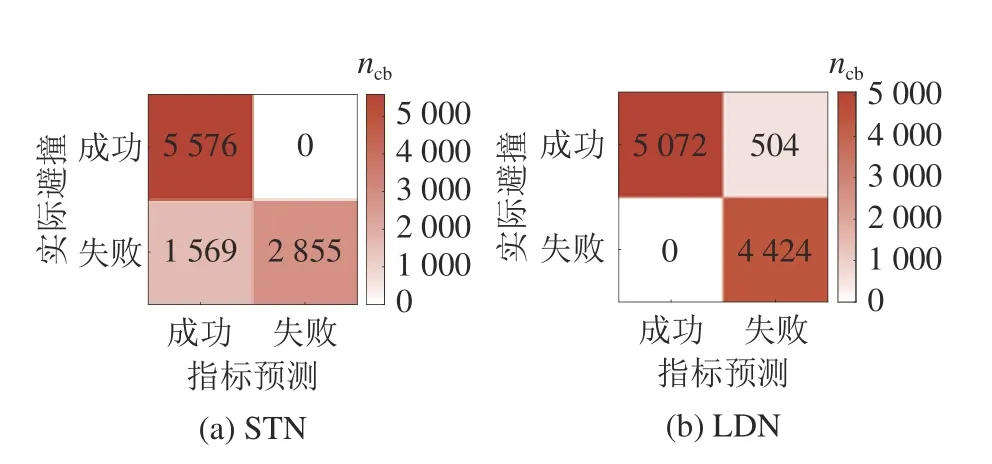
图12 高附着系数路面不同风险指数的混淆矩阵Fig.12 Confusion matrix of different threat numbers for high adhesion coefficient

4.2 中等附着系数( µ=0.7 )路面极限工况的风险指数准确性验证

随机分布生成如图13 所示的10 000 例测试场景，取纵向速度为[60, 100] km/h，避撞距离为[10, 40] m，2 种风险指数的预测结果与实际避撞结果如图14 所示.分析可以得到STN 预测值夸大了车辆的转向能力，LDN 预测值则低估了车辆的转向能力.总体来说，LDN 准确率为98.50%，STN 准确率为81.71%， LDN 准确性相较STN 有明显提高.

图13 中等附着系数路面测试场景的参数随机分布Fig.13 Random distribution of parameters for medium adhesion coefficient test scenario

图14 中等附着系数路面不同风险指数的混淆矩阵Fig.14 Confusion matrix of different threat numbers for medium adhesion coefficient

4.3 低附着系数( µ=0.4 )路面极限工况的风险指数准确性验证

随机分布生成如图15 所示10 000 例测试场景，取纵向速度为[40, 60] km/h，避撞距离为[10, 40] m，2 种风险指数的预测结果与实际避撞结果如图16 所示.分析可以得到STN预测值夸大了车辆的转向能力，LDN 预测值则低估了车辆的转向能力.总体来说，LDN 准确率为98.05%，STN 准确率为87.54%， LDN 准确性相较STN 有明显提高.

图15 低附着系数路面的测试场景参数随机分布Fig.15 Random distribution of parameters for low adhesion coefficient test scenario

图16 低附着系数路面不同风险指数的混淆矩阵Fig.16 Confusion matrix of different threat numbers for low adhesion coefficient

验证实验结果表明，在各种附着系数路面下，对比STN，本研究提出的风险指数在极限工况的预测准确性均有提升.

4.4 一般工况下风险指数适用性验证

为了验证LDN 在一般工况下的适用性，在µ=1.0，取纵向速度为[20, 100] km/h，避撞距离为[30, 50] m；在 µ=0.7 ，取纵向速度为[20, 80] km/h，避撞距离为[30, 50] m；在 µ=0.4 ，取纵向速度为[20, 60] km/h，避撞距离为[30, 50] m；进行仿真实验，对比验证LDN 和STN，结果如图17 所示.分析可知，在一般工况中，STN及LDN 均能准确判断当前工况能否完成避撞，说明LDN 具有该工况的适用性.

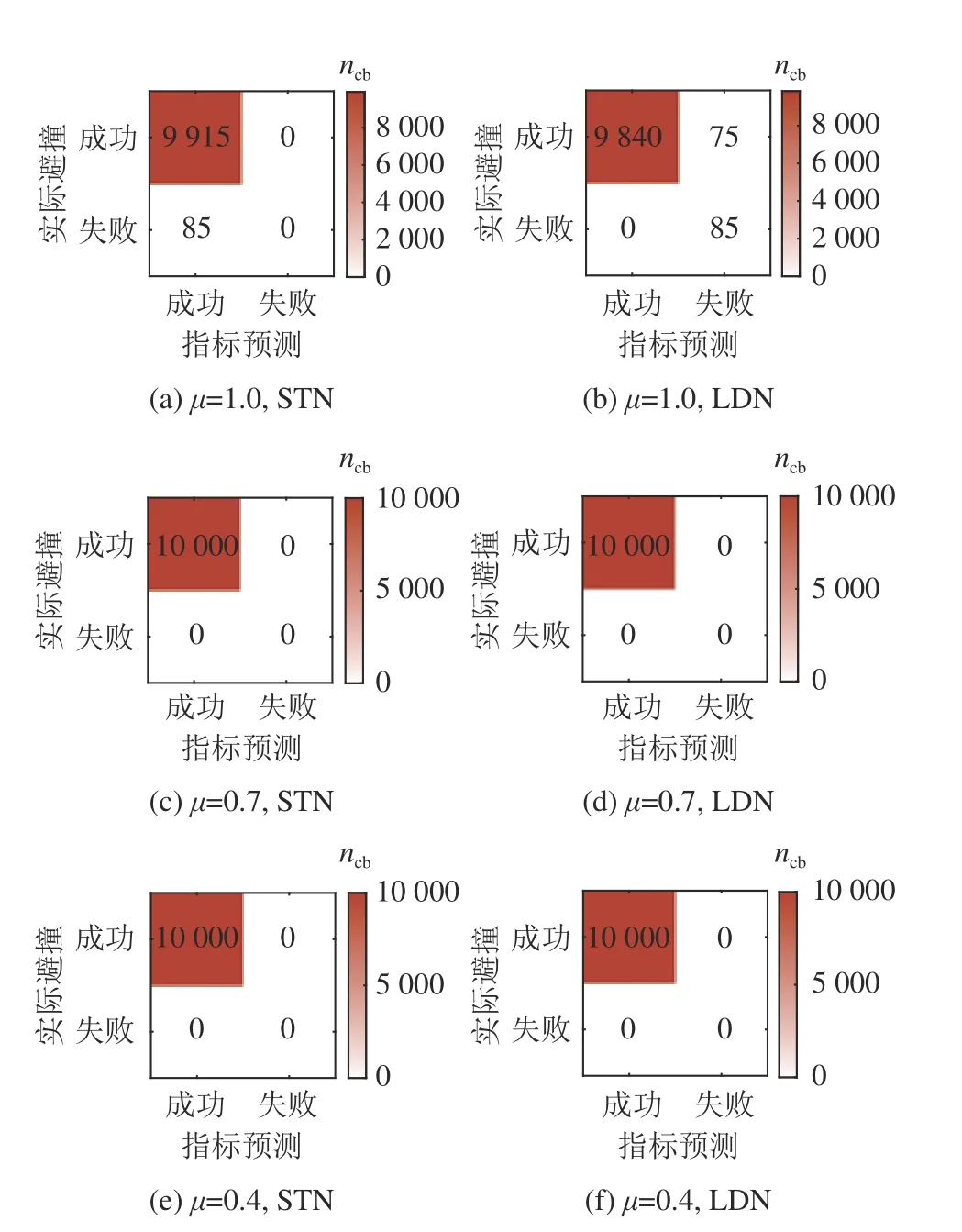
图17 不同附着系数路面的一般工况实验结果混淆矩阵Fig.17 Confusion matrix of normal situation results under different adhesion coefficient

4.5 不同侧向位移的风险指数准确性验证

为了验证LDN 在与不同类型前方车辆或障碍物避撞时所需侧向位移的普适性，在 µ=1.0 ，添加Wo=1 m 、Wo=3 m 2 组实验条件，与Wo=2 m进行仿真对比实验，对比验证LDN 和STN，结果如图18 所示.分析可知，在不同侧向位移条件下，对比STN，LDN 在极限工况的预测准确性均有提升.

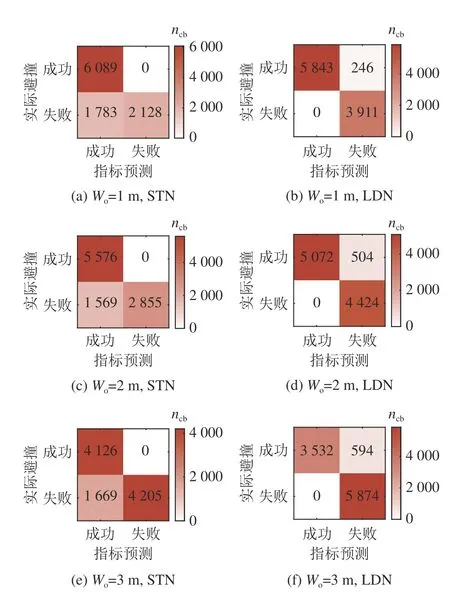
图18 不同侧向位移实验结果混淆矩阵Fig.18 Confusion matrix of different lateral displacement results

5 结 语

本研究考虑大侧向加速度下横向载荷转移效应对轮胎侧向力和垂向力耦合效应的影响，引入横向载荷转移系数提高了转向前馈控制的准确度.高、中、低期望侧向加速度的阶跃转向仿真实验证明，对比单轴模型和单轮模型，考虑横向载荷转移的前馈控制方法在大侧向加速度下控制精度有较大提升.本研究提出以阶跃转向实验模拟车辆转向避撞，得到最大可达侧向位移以精确反映车辆的转向避撞能力.对比STN 以路面附着约束评估车辆转向避撞能力的方式，以阶跃转向仿真实验得到的侧向位移可以更好地描述车辆转向避撞过程的非线性和瞬态特性，侧向位移作为指标更直接地反映了避撞条件.采用蒙特卡洛法分别在高、中、低附着系数路面极限工况、一般工况及不同侧向位移下随机生成10 000 例避撞场景，STN、LDN 的预测结果和实际避撞结果的对比验证证明本研究提出的风险指数在极限工况对车辆能否通过转向进行避撞判断更准确，且在一般工况和不同侧向位移具有适用性.本研究不足之处在于1）角阶跃转向实验未基于实车条件展开，下一步计划针对实际车辆和工况进行研究2）面对不稳定的路面附着系数条件LDN 预测效果不佳，下一步计划实现任意道路条件下避撞风险的准确预测.