基于集成概率模型的变阻抗机器人打磨力控制

郭万金，赵伍端，利乾辉，赵立军，曹雏清

(1.长安大学 道路施工技术与装备教育部重点实验室，陕西 西安 710064；2.哈尔滨工业大学 机器人技术与系统国家重点实验室，黑龙江 哈尔滨 150001；3.芜湖哈特机器人产业技术研究院有限公司，博士后工作站，安徽 芜湖 241007；4.长三角哈特机器人产业技术研究院，安徽 芜湖 241007)

现代高端装备制造业对工件的尺寸精度和表面质量要求越来越高.小批量、不同形状的工件多采用人工打磨方式进行精加工，存在一致性差、生产效率低的问题[1].机器人打磨以高灵巧性、低成本的特点正成为越来越重要的工件柔顺打磨作业实现途径.基于工业机器人的打磨技术已成为高端制造业中连续接触式作业（如打磨和抛光）的有力抓手，是解决人工作业工作效率低、改善工作环境和提升工件加工质量的重要工具之一.高性能打磨工业机器人作为新兴产业和技术的重要载体和现代产业的关键装备，不仅是持续促进生产水平提高的强力支撑，而且有力推动了智能制造的高质量发展[2-5].

针对主动柔顺控制打磨作业，机器人末端执行器的性能直接影响打磨作业的柔顺性，其中对具有力控功能且能够实现力位解耦控制的末端执行器开展的相关研究是当前的主要研究方向.阻抗控制是实现主动柔顺力控制的有效方式，其通过调节系统刚度实现输出力的柔顺调控.为了解决机器人末端执行器在跟踪未知曲面工件时接触力难以保持恒定的问题，Zhang 等[6]建立机器人末端执行器与工件表面的接触模型和力映射关系，提出基于强化学习算法的机器人力控制方法.甘亚辉等[7]针对未知刚度及位置多变工况，设计自适应变阻抗力跟踪控制方法，通过建立阻抗模型来适应多变工况刚度的不确定性，并根据机器人末端与多变工况之间接触力的变化在线自适应调节阻抗模型参数.李超等[8]提出基于强化学习的学习变阻抗控制方法，将高斯过程模型作为系统的变换动力学模型，在成本函数中加入能量损失项，实现了误差和能量的权衡.Zhou 等[9]基于机器人系统与环境的接触模型，采用自适应阻抗实现了打磨力控制和位置跟踪控制.Shen 等[10]提出基于模糊理论的自适应阻抗控制，通过递归最小二乘迭代计算估计环境参数，使得控制系统在没有环境先验信息的情况下跟踪期望打磨力.Zhong 等[11]将自适应阻抗控制与基于非线性扰动观测器的滑模控制器相结合，实现了对期望接触力和轨迹的跟踪.上述针对机器人自适应打磨力控制采用迭代类计算的研究方法[8,10-11]，存在数据更新过程慢与效率低的局限，对于需要严格控制打磨力精度和超调量的曲面工件机器人打磨作业，在打磨力控制的实时性和稳定性方面存在一定的不足.机器人的工件柔顺打磨作业对机器人系统稳定性和鲁棒性的要求较高，通常需要严格控制打磨力的精度和超调量.

本研究采用基于位置的阻抗控制作为底层的打磨力控制结构，基于集成贝叶斯神经网络（Bayesian neural network，BNN）模型的强化学习，提出主动自适应变阻抗的机器人打磨力控制方法.1）基于BNN 的集成概率模型（ensemble probabilistic model，EPM）拟合打磨作业过程的概率动力学模型，以描述控制输入和工具与工件接触状态之间的不确定性.2）采用固定轨迹采样法和随机轨迹采样法开展模型预测控制（model predictive control，MPC），利用协方差矩阵自适应进化策略（covariance matrix adaptation evolution strategy，CMA-ES）算法对模型预测过程进行动态参数优化，求解模型预测控制的最优解集.3）在成本函数中引入基于方差的能量损失项，优化求解获取最优阻抗参数，用于主动自适应更新阻抗参数，实现机器人打磨力主动自适应控制.4）在所构建的机器人打磨系统虚拟样机平台上，开展机器人与工件交互环境的强化学习主动自适应打磨力控制仿真与分析，验证所提方法的有效性.

1 基于柔顺浮动力控末端执行器的机器人打磨系统

1.1 柔顺浮动力控末端执行器设计

机器人打磨系统主要由工业机器人与末端执行器构成.末端执行器的柔顺打磨作业由主动力控制技术实现，末端执行器的位置和姿态（简称位姿）由工业机器人控制.工件的打磨质量与材料去除率有关，根据Preston 材料去除理论，材料去除率与工具对工件的法向打磨力正相关[12].为了实现材料去除率可控，保证打磨质量，提高机器人打磨系统动态响应性能[13]，设计柔顺浮动力控末端执行器[14]，如图1 所示.该末端执行器通过音圈电机驱动打磨主轴往复直线轴向平移运动，实现打磨工具平移浮动调节，主动柔顺控制实现法向打磨力稳定准确控制，打磨主轴带动打磨工具高速旋转运动，轴向平移和旋转运动互不干扰，两者的调节控制便捷.应用主动力控制技术进行法向打磨力稳定准确控制，并通过机器人进行打磨位姿控制，降低对工业机器人本体的力控制要求，减小力控制和位姿控制的复杂性.

图1 柔顺浮动力控末端执行器[14]Fig.1 Compliant floating force-controlled end-effector [14]

1.2 机器人打磨系统虚拟样机构建

采用Adams 构建机器人打磨系统虚拟样机，如图2 所示，该系统虚拟样机由柔顺浮动力控末端执行器、六自由度串联工业机器人和曲面工件组成.通过Adams Controls 插件将打磨系统虚拟样机导出为控制机械系统模型后导入Matlab/Simulink仿真控制系统，为机器人打磨系统自适应打磨力控制提供联合仿真平台.Matlab/Simulink 仿真控制系统虚拟样机的输入分别为机器人关节变量、音圈电机输出力；输出分别为所设计末端执行器打磨主轴的轴向位置变化量、工具末端坐标系{E}的位置和机器人工具坐标系{T}表示的工件对工具的反作用力

图2 机器人打磨系统虚拟样机Fig.2 Virtual prototype of robotic grinding system

2 基于集成概率模型的强化学习主动自适应变阻抗控制

机器人打磨作业接触环境具有较强的时变耦合非线性动力学特性，而且工件型面各异、形状复杂，致使机器人柔顺打磨作业适应性差问题愈加严重.本研究基于集成概率模型的强化学习，提出主动自适应变阻抗的机器人打磨力控制方法，以实现主动自适应机器人法向打磨力准确控制，提升机器人柔顺打磨作业的适应性和稳定性.

2.1 变阻抗控制器设计

Hogan[15]针对接触作业的力控制问题，提出阻抗控制方法.有学者将阻抗控制分为基于力的阻抗控制和基于位置的阻抗控制，后者可以实现较高的位置控制精度[16].基于位置的阻抗控制基本思想是将位置控制器作为控制系统的内环，将阻抗控制器作为控制系统的外环，外环产生位置修正量，内外环控制共同作用构成闭环控制回路.通过反馈力计算阻抗控制器输出的位置补偿量，调节内环位置控制器的输入位置，实现对接触过程的力控制.将基于位置的阻抗控制设计为变阻抗控制器作为控制外环，通过变阻抗控制实现对内环的位置控制系统的自适应补偿，从而实现对机器人打磨力的柔顺控制，提升机器人打磨作业的柔顺性和鲁棒性.如图3 所示为该变阻抗控制的控制框图，数学模型为

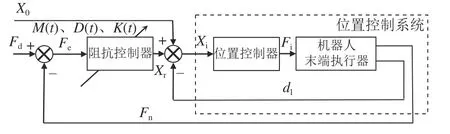
图3 变阻抗控制的控制框图Fig.3 Control block diagram of variable impedance control

式中：Fe为法向打磨力Fn与期望打磨力Fd的偏差，作为变阻抗控制器的输入；通过数学模型的传递，算出对位置控制系统输入的补偿量Xr，将Xr与期望位置X0及位置变化量dl叠加，作为位置控制系统的输入Xi，再将位置控制器的输出Fi作为机器人末端执行器的输入，其中dl由位置控制系统的反馈位置信号提供；M(t)、D(t)、K(t)分别为变阻抗控制器的时变惯性系数、时变阻尼系数和时变刚度系数.

2.2 基于集成概率模型的强化学习主动自适应参数调节

基于集成概率模型的强化学习，提出主动自适应变阻抗的机器人打磨力控制方法.1）构建基于BNN 的集成概率模型，描述机器人打磨系统在时变非线性接触环境下引起的系统不确定性.采用BNN 模型描述控制系统控制量和状态量之间的分布关系，量化由于测量引起的认知不确定性；根据多次采样的子数据集拟合多个BNN 模型，构建集成概率模型，描述系统随机不确定性.2）结合构建的集成概率模型，采用模型预测控制，根据工具与接触工况的交互状态，主动自适应更新阻抗参数，获取最优控制量，形成机器人打磨系统根据接触工况环境状态主动自适应变阻抗调节策略，以适应不同接触工况环境和打磨作业任务需求，提高机器人柔顺打磨作业的自适应性和鲁棒性.

2.2.1 基于BNN 的集成概率模型构建 在打磨工具与工件的接触作业过程中，机器人打磨系统的控制量与工具及工件接触的状态量具有马尔科夫性[17]，将机器人打磨系统的动力学传递函数描述为

式中： (xt,ut)、xt和ut分别为系统的状态动作对、状态观测量（状态空间）和控制输入量（动作空间）；f为系统的动力学传递函数，可以表示该马尔科夫过程的状态转移概率.将状态的微分作为训练的输出量，可以近似学习动力学模型的梯度，与直接学习状态的值相比，学习状态的微分能够更清晰地描述系统的动态特性，因此更具优势[18].

针对工具与工件接触状态和阻抗参数的非线性关系，以t时间段工具与工件的打磨力的均值和标准差作为状态观测量[19]，以阻尼系数和刚度系数作为控制输入量，令，则t时间段与t-1 时间段状态量的微分为

将 Δxt作为概率动力学模型的输出，则系统的动力学传递函数描述为

机器人打磨作业时，由于工具与工件接触时产生的不确定性扰动，导致控制系统存在不确定性.要实现对打磨作业的稳定、准确控制，须考虑系统模型的不确定性，包含1）机器人时变耦合非线性打磨作业接触环境引起的系统随机不确定性，2）测量误差引起的认知不确定性.这2 种不确定性难以用精确的数学模型描述，因此采用基于BNN 的集成概率模型从统计学角度进行描述.

1) BNN 模型构建.BNN 模型将传统BP 神经网络的权重以概率分布的形式描述，建立输入和输出之间的概率分布关系，利用贝叶斯定理和变分推断思想，以证据下界（evidence lower bound，ELBO）作为损失函数训练网络权重，使拟合的BNN 在有先验数据的区域表现出较小的不确定性，在无先验数据的区域表现出较大的不确定性.利用BNN 模型拟合控制系统，描述控制系统控制量和状态量之间的分布关系，即可量化由于测量引起的认知不确定性.BNN 模型对网络的可训练网络模型参数的权重进行重参数化[20]，使网络参数以概率分布的形式呈现.假设网络模型输出Y的分布为

可训练网络模型x中的参数 θ 服从先验分布θ ～N(0,1)，由于输入与模型参数之间具有独立性，输入与输出描述为网络参数的映射，根据贝叶斯定理，模型参数w或b用H代表，则H的后验概率为

式中：D为观测数据.对于复杂的深度贝叶斯神经网络模型，后验分布的高维性与非凸性使得证据（边缘分布）难以计算[21].引入变分推断[22]，通过参数化后验分布（变分后验分布）逼近真实后验.变分推断的准确度可用变分后验分布与真实分布的近似度描述.KL 散度（Kullback Leibler divergence）是描述2 种分布近似度常用的方法，其通过Shannon 信息熵理论描述概率分布之间的差异性.假设样本真实后验概率为P(H|D) ，变分后验分布为qθ(H) ，则变分后验对真实后验的近似度为

式中：H′为网络模型参数积分因子.为了避免真实后验P(H|D) 复杂的计算过程，引入ELBO 作为深度神经网络模型的损失函数：

即通过最小化L(θ) ，使预测的输出分布更接近于真实输出分布.P(D) 为边缘似然函数，最小化KL散度DKL(q||P) 等同于最大化ELBO，即最大化损失函数.ELBO 梯度不可解，为此引入蒙特卡洛估计法，计算损失函数ELBO 对模型参数 θ的 负梯度，为

式中：NM为蒙特卡洛采样次数.按照ELBO 的负梯度方向对网络参数不断更新，以达到网络输出逼近真实分布的目的，梯度下降算法采用随机梯度下降法（stochastic gradient descent，SGD）实现.

2) 集成概率模型构建.机器人时变耦合非线性打磨作业接触环境引起的系统随机不确定性可以通过集成概率模型的方法来描述，即根据多次采样的数据集拟合多个BNN 模型，构建集成概率模型，联合描述系统随机不确定性[23]，表征机器人打磨系统的打磨工具与工件接触状态和阻抗参数之间的非线性关系.采用自助法（Bootstrapping），从原始数据集中有放回地均匀抽样创建模拟数据集，将有限样本经由K次重复抽样，建立足以代表母体样本分布的K个子样本.利用自助采样的K个样本，训练出K个BNN 模型，利用模型预测采样轨迹法合成为集成概率模型.动力学模型f(x,u)可用集成概率模型中K个BNN 模型的输出分布Pi(x,u)代替，具体训练过程如图4 所示.

图4 集成概率模型的训练过程Fig.4 Training process of ensemble probabilistic model

2.2.2 集成概率模型预测控制 在已知系统传递函数的基础上，根据初始状态量和控制量算出一系列预测域的状态量和控制量轨迹；采用反馈校正，对状态量和控制量进行优化；在控制过程中，采用滚动时域优化方法，在每个控制周期进行局部优化，提高控制系统的抗扰性和稳定性[24].通过非线性状态传递函数，求解h步预测域的状态轨迹xt,xt+1,···,xt+h：

根据状态和控制序列以及状态量的权重Q、控制量的权重R，求得目标函数：

对Loss 进行优化，得到最优控制序列：

1) 模型预测轨迹采样.训练的集成概率模型中有K个BNN 模型，须在预测时对BNN 模型的利用方式进行分配.采用固定轨迹采样法与随机轨迹采样法的随机混合进行分配.固定轨迹采样法：每个训练时间段t选取同1 个训练好的BNN模型进行模型预测控制；在下次预测时，预测模型更换为下个训练好的BNN 模型.随机轨迹采样法：每个预测时间段t随机地选取1 个训练好的BNNt，每步均利用不同的模型进行模型预测控制.这2 种轨迹采样方法，分别从整体和局部2 个角度描述系统的固有随机性，使得模型具有更好的泛化能力.

2) 基于协方差矩阵自适应进化策略算法的参数优化.由于不宜采用集成概率模型计算梯度，选择非梯度优化算法解算最优控制量.CMA-ES算法作为数值优化算法，在求解非梯度的优化问题时具有全局收敛和收敛快速的优点[25]，主要实现步骤如下.a) 采样重组：采用多变量正态分布生成新的样本点.在第z代中，k个子代样本点生成式为

式中：m(z)∈Rn为第z代中搜索分布的平均值，σ(z)∈R+为搜索步长，C(z)∈Rn×n为第z代的协方差矩阵， λ 为种群大小，n为优化问题的维度；随机获取第0 代的均值m(0).搜索分布的新一代平均值：

b) 全局步长自适应：使用共轭进化路径更新步长，

式中：cσ为步长累积的学习率； µeff为方差有效选择权重；E为求解期望值，I为单位矩阵，dσ为步长更新的阻尼参数，

c) 协方差矩阵适应：与步长自适应类似，进化路径

式中：ccov为协 方 差 更新的学 习 率， µcov为 矩 阵 秩更新的加权系数，

更新m(z)、wi和 σ(z+1)等重要参数，获取模型预测控制策略优化问题的最优解集.

2.2.3 基于集成概率模型的强化学习主动自适应变阻抗的机器人打磨力控制 为了提高机器人打磨力控制的稳定性，在成本函数（奖励惩罚策略）中引入基于方差的能量损失项，减小机器人打磨时的不确定性扰动引起的不稳定性，提高系统的抗干扰能力.假设目标状态为xtar，设定自适应参数调节策略的单步成本函数为

其中等号右边第一项为瞬时状态误差项，第二项为瞬时能量成本项，umax为最大控制输入量.为了量化自适应参数调节策略的性能，定义时间段tend的总成本为

将式(28)作为自适应参数调节策略的评价指标，其中 ξ 为tend的成本序列C方差的权重，std( )为标准差函数.利用CMA-ES 算法，优化求解使得总成本R最大对应的控制量uot作为下一步的控制量.基于集成概率模型的强化学习算法对应伪代码如算法 1 所示.根据状态观测量和控制输入量，利用CMA-ES 算法对状态观测量进行迭代优化.将求解的最优控制量uot作为所提方法的机器人末端执行器打磨作业的阻抗控制器的变阻抗参数，结合式(2)、(3)进行实时主动自适应变阻抗参数的机器人打磨力控制，控制框图如图5 所示.

图5 基于集成概率模型的主动自适应变阻抗的机器人打磨力控制框图Fig.5 Block diagram of robotic grinding force control with active adaptive variable impedance based on ensemble probabilistic model

集成概率模型EPM 采用离线训练方式，所使用的采集观测数据只包含工具与工件接触模型信息，不包含外部环境信息，训练后的环境对机器人打磨力控制系统而言是未知环境.当环境改变后，所训练的集成概率模型仍可结合CMA-ES 算法实时优化求解最优阻抗参数.训练后的变阻抗控制器适用于不同形状的曲面和环境刚度的工况.本研究提出的基于集成概率模型的强化学习主动自适应变阻抗的机器人打磨力控制方法，强化学习包含有系统不确定性的工具与工件的交互过程，通过经训练的集成概率模型EPM 描述状态观测量xt与控制输入量ut的关系，采用CMA-ES算法求解模型预测控制策略优化问题描述的最优解集控制输入量ut，获得与工作环境主动自适应的变阻抗参数，主动自适应调节工具与工件之间的阻抗特性，将打磨力偏差经变阻抗控制器产生的自适应修正补偿量作用于位置控制系统，实现打磨力控制，提高机器人打磨系统的自适应性能.

3 机器人自适应打磨作业仿真实验

针对中小型曲面工件，采用所提机器人打磨力控制方法，提升打磨力控制的稳定性与准确性，使得打磨力控制能够主动自适应调节阻抗控制参数，保持打磨力的恒定，提高机器人柔顺打磨作业的适应性和稳定性.在航空制造领域，航空发动机含有数千枚叶片，加工后叶片表面粗糙度要求较高，其磨抛加工任务量占近一半的叶片制造总工作量，由于叶片不断改进导致种类繁多，形状复杂，本研究选取该领域具有曲面典型特征的叶片开展机器人打磨作业仿真实验，验证所提方法的有效性.1）采用具有平滑性特点的NURBS 曲线规划机器人打磨轨迹，以实现打磨作业过程的位置、速度等的平滑过渡.2）开展机器人与工件交互环境的强化学习主动自适应打磨力控制仿真与分析，验证所提方法的有效性.

3.1 机器人打磨路径和打磨轨迹规划

1) 作业空间打磨路径和打磨姿态规划.如图6(a)所示，采用子午线作为打磨作业路径，利用NURBS 曲线插值对打磨作业笛卡尔空间位置进行轨迹规划.在叶片上根据子午线的形状，采样48 个路径点作为型值点，其空间位置和相对应的叶片曲面法向量如图6(b)所示.将型值点作为控制点，利用5 次NURBS 曲线插值，对打磨路径进行插值平滑处理，求得经过平滑后的机器人末端执行器的作业工具末端点空间位置.为了实现机器人打磨姿态平滑过渡，将姿态矩阵转换为单位四元数，利用单位对数四元数法，将单位四元数转换为三维空间点[26]，对转换后的三维空间点进行5 次NURBS 曲线插值.根据打磨路径和打磨姿态规划结果，获得机器人打磨系统对应打磨工具轨迹如图7 所示.

图6 叶片工件、规划路径点和曲面法向量Fig.6 Blade workpiece, planned path points and surface normal vectors

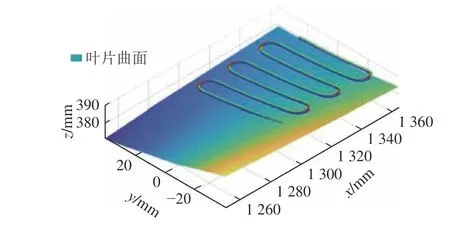
图7 机器人打磨的工具轨迹Fig.7 Tool trajectory of robotic grinding

2) 关节空间打磨轨迹规划.5 次NURBS 曲线插值使机器人关节空间的角速度、角加速度和急动度（Jerk）均具有平滑性.采用分段插值轨迹规划方法，对打磨作业路径对应的机器人各关节角进行5 次NURBS 曲线插值，规划打磨轨迹.其中t=0～3 s，机器人打磨系统工具末端点从起始位置（对应机器人各关节角为零）移动到规划打磨路径的起始点；t>3 s，机器人打磨系统工具末端点从规划打磨路径的起始点开始，沿着规划路径，执行打磨作业，此时采用5 次NURBS 曲线插值，对机器人各关节进行轨迹规划.所规划的机器人各关 节 的 角 度 θ 、角 速 度 ω 、角 加 速 度a及 急 动 度J曲线，如图8 所示.各关节角度和角速度变化较为平缓且没有突变，角加速度和急动度的变化也较小，分别不超过0.4°/s2和1.5°/s3.

图8 机器人各关节的角度、角速度、角加速度及急动度曲线Fig.8 Curves of robotic joints for angle, angular velocity, angular acceleration and jerk

3.2 机器人强化学习主动自适应打磨力控制仿真

将所提机器人打磨力控制方法设计为机器人强化学习自适应打磨力控制器.在控制器中设置集成概率模型的BNN 数量为5，每个BNN 均具有2 层64 个神经元的隐藏层，激活函数选用Swish函数，每次自助法采样数量为总体样本数量的50%，且对网络权重作L2 正则化，采用小批量随机梯度下降法，利用Adam 优化算法优化训练过程，单个BNN 模型的训练迭代次数设置为3.0×104次.选取初始阻抗参数M(t0)=3 kg、D(t0)=30 N·m/s和K(t0)=2 N/m，并设阻抗参数的待训练参数取值范围分别为D(t)∈[10, 200]和K(t)∈[0, 20].分别设打磨期望力（即打磨作业目标状态量）为15、20、30 N，期望的打磨力方差Fes=0，即xtar对应取为[15, 0]、[20, 0]和[30, 0]，开展自适应打磨力控制对比仿真.当取xtar=[20, 0]时，训练后的机器人强化学习自适应打磨力控制器，分别对铝合金工件和碳钢工件进行打磨仿真，其材料刚度分别为3.5×104、1.0×105N/m.设置仿真时间为20 s，仿真步长为0.01 s；将仿真时间分为10 个参数修正段，每段时间长为2 s（即对应为200 步）.在每个参数修正段结束后，根据所提方法，主动自适应调节阻抗参数.在Matlab/Simulink 中，构建机器人强化学习自适应打磨力控制器，通过对机器人打磨系统虚拟样机联合仿真控制，按照子午线打磨路径，对叶片进行打磨作业仿真实验.第一次训练时，1）在阻抗参数取值范围内随机取10 组待训练参数D(t)、K(t)，t=1～10 s，获取初始的状态量数据集xt和控制量数据集ut.2）对数据集进行自助法采样，获取5 个子数据集.3）分别利用5 个数据集训练EPM 中的5 个BNN 模型.在第一次训练结束后，后续每次均采用所提方法更新阻抗参数.

对于不同的打磨期望力，经过多次训练，机器人打磨系统对选取叶片的打磨力获得有效控制，打磨力跟踪误差方差和均值均减小，实现了打磨力的有效跟踪控制.经过不同次数的训练，机器人的不同打磨期望力对应的打磨力曲线如图9 所示，训练过程的不同预测段m对应的奖励值RV 曲线如图10 所示；不同训练次数 ξ 的打磨力绝对 跟 踪 误 差fd对 应 最 大 值、方 差和 均 值如表1 所示.当打磨期望力为20 N、期望的打磨力方差=0 时，训练后的自适应打磨力控制器对不同刚度的铝合金工件和碳钢工件仿真对应的打磨力曲线如图11 所示，与打磨力绝对跟踪误差如表2所示.由表1 可知，随着训练次数的增加，打磨力绝对跟踪误差的最大值、方差和均值均逐渐变小，表明随着训练的进行，均在一定程度内提高了打磨力控制的稳定性、准确性和精度，降低了力控制的超调量.由图11 和表2 可知，训练后的变阻抗控制器对于不同环境刚度，仅需数次训练微调之后，即可达到较好的跟踪效果.

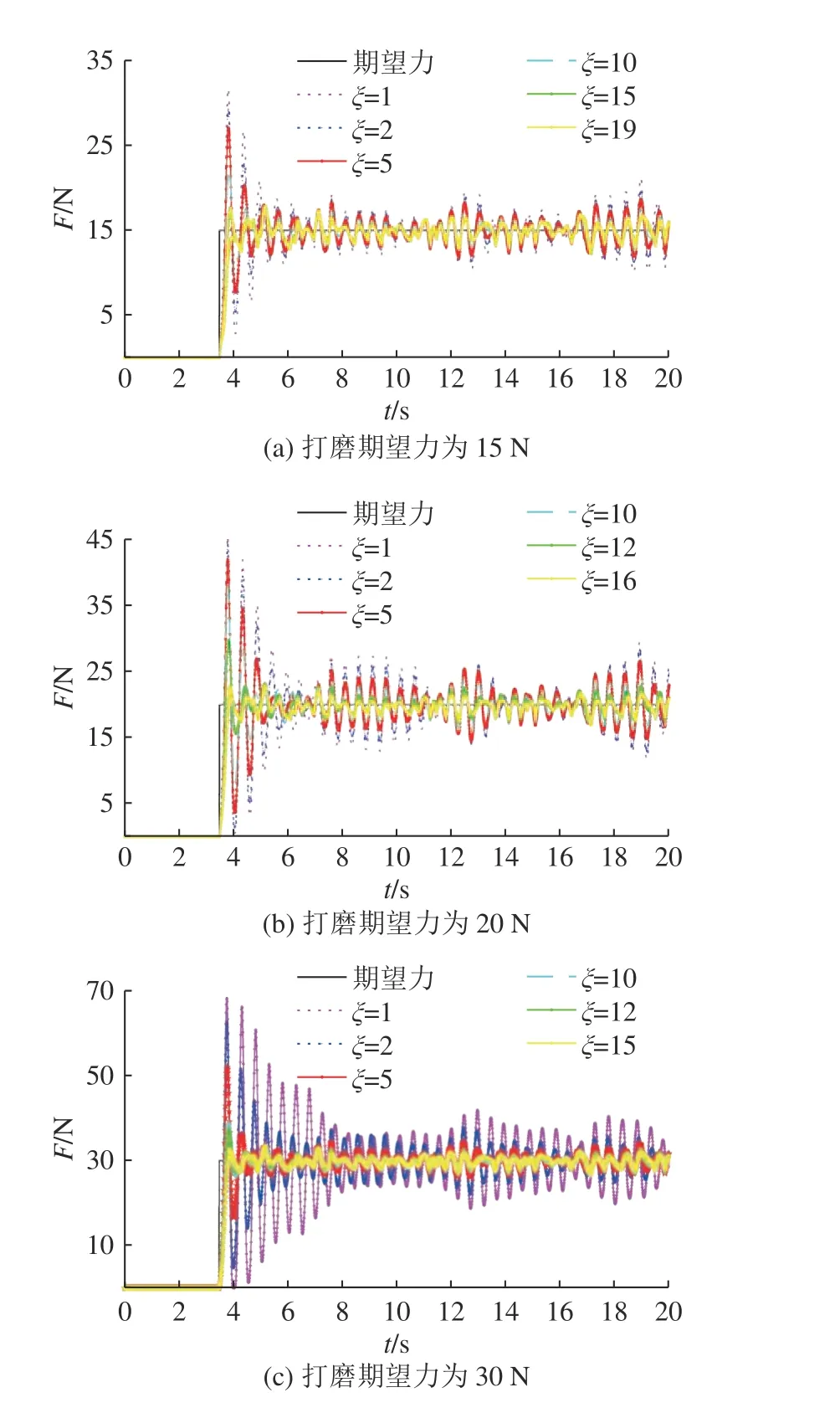
图9 不同打磨期望力在不同训练次数下的打磨力曲线Fig.9 Grinding force curves of different expected grinding force after multiple trainings

图10 不同打磨期望力在不同训练次数下的奖励值曲线Fig.10 Reward curves of different expected grinding force after multiple trainings

图11 不同刚度工件的打磨力曲线Fig.11 Grinding force curves for workpieces with different stiffnesses

通过不同期望力的仿真实验可知，所提方法仅在十几次训练后，机器人打磨系统即可使打磨力绝对跟踪误差的最大值、方差和均值均减小至某一较小值，同时对于不同刚度工件也具有较好的打磨力跟踪性能，较好地实现了机器人打磨系统的主动自适应变阻抗打磨力控制，验证了所提方法的有效性.对于恒定打磨力控制，模糊自适应变阻抗控制是常用方法，当其对某一种恒定打磨期望力调节好适宜模糊逻辑控制参数之后，对其他恒定打磨期望力的跟踪效果通常会变差，自适应性能不高[27-28].因此，当模糊变阻抗控制器对不同的恒定打磨期望力进行跟踪时，均应人为调整模糊逻辑参数.与之相比，本研究所提方法在自适应打磨力控制器经过离线训练后，对于跟踪不同的恒定打磨期望力不需要再次调整参数，仅通过少量训练即可实现变阻抗控制器的主动自适应参数调节，具有较强的自适应性.所提方法为机器人打磨系统对不同工件以不同期望恒定打磨力开展柔顺打磨作业提供了主动自适应柔顺恒力控制方法.

4 结 论

(1) 为了解决机器人对工件柔顺打磨作业适应性差的问题，设计柔顺浮动力控末端执行器，并基于集成贝叶斯神经网络模型的强化学习提出主动自适应变阻抗的机器人打磨力控制方法.该方法1）根据打磨作业过程中工具与工件的接触状态信息，采用自助法构建多个子数据集，对多个贝叶斯神经网络进行训练，构成集成概率模型；2）使用CMA-ES 算法，预测阻抗控制器的阻抗参数，自适应求解当前工况状态的最优阻抗参数；3）将所提方法设计为机器人强化学习自适应打磨力控制器，实现法向打磨力对期望打磨力的自适应跟踪，提升机器人打磨力的稳定性和准确性.

(2) 采用Adams 和Matlab/Simulink 分别构建机器人打磨系统的虚拟样机和仿真控制系统，通过联合仿真，开展机器人与工件交互环境的强化学习主动自适应打磨力控制仿真与分析.结果表明，在期望打磨力分别为15、20 、30 N 的工况下，所提方法均在十几次训练后，机器人打磨系统即可实现从无法准确跟踪期望打磨力，训练到打磨力绝对跟踪误差减小至较小值，对不同刚度工件也具有较好的打磨力跟踪性能，验证了所提方法的有效性.

(3) 所提方法可为机器人柔顺打磨作业提供主动自适应机器人打磨力控制方法，具有一定的参考价值.

(4)后续在所提方法基础上，计划针对机器人打磨作业颤振这类非线性强扰动工况，深入开展机器人主动自适应打磨力控制研究，提高在强扰动环境下机器人主动自适应打磨力控制的鲁棒性.